VIGILANCIA EN SALUD

 

Pronósticos de mortalidad por enfermedades no transmisibles seleccionadas

 

Prognoses of mortality from non-communicable selected diseases

 

 

Gisele Coutin Marie

Especialista de II Grado de Bioestadística, Maestra en Ciencias en Informática, Unidad Nacional de Análisis y Tendencias en Salud Nacional, Ministerio de Salud Pública, La Habana, Cuba.

 

 

---

RESUMEN

El perfeccionamiento de la vigilancia constituye una de las principales funciones del componente estratégico del modelo de vigilancia en salud cubano y la obtención de pronósticos para reducir la incertidumbre en la toma de decisiones resulta crucial en un entorno variable donde es necesario percatarse tempranamente de los nuevos problemas. El uso de las técnicas de análisis de series temporales con fines de predicción se ha generalizado en el ámbito de la salud pública. Los alisamientos o suavizamientos exponenciales constituyen los métodos más utilizados para obtener pronósticos de series temporales debido a su simplicidad, eficiencia computacional y aceptable exactitud. En este trabajo se presentan los resultados obtenidos con la aplicación de estos métodos comparados con el ajuste de algunos polinomios en la obtención de pronósticos para la mortalidad por algunas enfermedades no transmisibles seleccionadas en los años 2007-2009. Como resultado fundamental se exponen los modelos de predicción para todas las causas de muerte que se caracterizan por tener errores de predicción pequeños e intervalos de predicción estrechos. Se concluye que los alisamientos exponenciales permiten la elaboración de modelos de manera relativamente simple y resultan muy útiles para la vigilancia de eventos de salud pues facilitan la toma de decisiones oportunas.

Palabras clave: Técnicas para pronósticos, series de tiempo, alisamientos exponenciales, ajuste de polinomios, técnicas estadísticas para la vigilancia.

---

ABSTRACT

The improvement of surveillance is one of the main functions of the strategic component of the surveillance model in Cuban health. The obtention of prognoses to reduce the uncertainty at the time of making decisions is crucial in a variable environment where the early detection of new problems is necessary. The use of techniques of analyses of temporary series with prediction ends is generalized in the public health sphere. The isolations or exponential smoothing are the most used methods to obtain prognoses of temporary series due to their simplicity, computational efficiency, and acceptable accuracy. In this paper we showed the results achieved with the application of these methods compared with the adjustments of some polynomials to attain prognoses for mortality from some non-communicable diseases selected between 2007 and 2009. The prediction models for all death causes characterized by little prediction errors and narrow prediction intervals are exposed as the main result. It was concluded that exponential isolations allow to design models in a relatively simple way and are very useful for the surveillance of health events, since they make easy the opportune decision making.

Key words: Prognosis techniques, time series, exponential isolations, polynomial adjustments, statistical techniques for surveillance.

---

 

 

INTRODUCCIÓN

La vigilancia en salud en Cuba se ha estructurado sobre la base de 3 componentes básicos: táctico, estratégico y evaluativo. Entre las principales funciones del componente estratégico están el análisis, síntesis e interpretación de información sobre perfiles de salud y enfermedad, la ejecución de estudios especiales para apoyar la toma de decisiones y la realización de estudios de tendencias, a mediano y largo plazo, de los daños a la salud y sus determinantes, así como la emisión de pronósticos y el perfeccionamiento de las técnicas utilizadas para obtenerlos.¹

La generación de pronósticos permite perfeccionar los mecanismos para reducir la incertidumbre en la adopción de decisiones en un entorno donde se suceden cambios frecuentes y donde resulta necesario percatarse tempranamente de las nuevas necesidades y áreas problema.

Los métodos para obtener predicciones pueden clasificarse en cualitativos y cuantitativos, en los primeros se recurre básicamente a la opinión de expertos y en los segundos, se trata de obtener modelos matemáticos utilizando la información histórica acumulada mediante análisis de series de tiempo. En la actualidad se ha universalizado el uso de las técnicas de análisis de series temporales con fines de predicción.²

Generalmente, se desea obtener un modelo que describa la mayoría de las particularidades de la serie, permitiendo de esta manera un conocimiento más profundo y real, así como una proyección más eficiente en el futuro. Sin embargo, la obtención de modelos de pronósticos constituye un proceso complejo donde resulta esencial la evaluación de la bondad de ajuste del modelo y la medición de la exactitud de su capacidad predictiva.

Una de las principales dificultades que tiene el proceso de predicción, se produce al establecer los vaticinios acerca de la conducta futura de un evento partiendo del análisis de su conducta pasada. Al actuar de este modo, con el modelo de pronóstico obtenido se está extrapolando hacia el futuro el comportamiento anterior de la serie, es decir, que tácitamente se acepta que los factores que han generado un evento cualquiera deben continuar comportándose de la misma forma. Sin embargo, muy a menudo esos factores sufren variaciones ya que el proceso que genera la serie es muy dinámico. En el ámbito de la salud pública, estas variaciones son múltiples y van desde las intervenciones realizadas para controlar problemas de salud hasta las modificaciones del comportamiento de los eventos de salud por múltiples causas (desastres naturales, crisis económicas, variaciones biológicas, etcétera).^3,4 No obstante, con frecuencia se asume una cierta estabilidad de estos factores para que tenga sentido al menos la predicción en horizontes de tiempo cortos, en los cuales resulta necesario disponer de valores estimados que faciliten el proceso de la toma de decisiones.

La determinación de la idoneidad del modelo escogido para el pronóstico se realiza analizando los errores de predicción; la forma más sencilla de obtenerlos sería comprobando las discrepancias existentes entre el valor pronosticado y el real, pero para ello habría que esperar el momento futuro y comparar ambos valores y eso no resulta práctico, por eso se prefiere obtener los errores analizando la diferencia entre los comportamientos ya observados y los esperados, esto es, analizando cuán bien predijo el modelo los valores de la serie que ya se han producido. Existen muchas medidas para resumir estas discrepancias pero la mayoría de los autores recomiendan la utilización del error cuadrático medio y el porcentaje de error medio absoluto, este último tiene la ventaja adicional que no se ve afectado por los cambios de escala en la variable de estudio. Otra medida de evaluación del error de predicción que no se ve afectada por los cambios en la escala del fenómeno y que además, penaliza los errores de predicción de gran magnitud es el coeficiente de desigualdad de Theil y sus 3 componentes o coeficientes parciales de desigualdad (proporción del sesgo, proporción de la varianza y proporción de la covarianza); pero tienen la desventaja de que generalmente no aparecen entre los índices que proponen los softwares para estas evaluaciones y deben ser calculados aparte.^5-7

Para la obtención de pronósticos en series temporales de periodicidad anual que se supone tengan tendencia, se han propuesto 2 grandes grupos de métodos: ajuste de curvas mediante polinomios de diferente grado y la utilización de filtros lineales (medias móviles o alisamientos exponenciales) para suavizar las fluctuaciones locales de la serie y estimar su comportamiento medio.⁸

El ajuste de diferentes curvas mediante la minimización del error medio constituye el procedimiento de elección para muchos dado que permite extrapolar la tendencia futura del evento, a lo que se añade el atractivo adicional de la abundancia de programas computacionales con los cuales pueden obtenerse estimaciones bastante razonables con un mínimo de conocimientos teóricos.^9,10 Sin embargo, algunos autores no lo recomiendan por la necesidad de evaluación previa del cumplimiento de supuestos (normalidad, independencia y homocedasticidad) que se sabe de antemano que generalmente, las series temporales no cumplen.^11,12

Por otra parte, se tiene que los suavizamientos o alisamientos exponenciales descritos casi simultáneamente por Holt (1957), Brown (1959) y Winters (1960) para obtener pronósticos en series temporales, no se basan en el cumplimiento de supuesto alguno y no pretenden hacer una caracterización formal de la serie de tiempo, sino dar elementos para un pronóstico rápido y efectivo basado en el análisis integrado de los componentes de la misma; con estos métodos se suavizan las fluctuaciones locales y se puede apreciar la tendencia y/o la estacionalidad de la serie.

Los nuevos valores se obtienen reestimando cada valor de la serie como una combinación lineal de los anteriores, con coeficientes determinados por el valor de las constantes de suavizamiento (a, b o s, según se trate de una serie sin tendencia, con tendencia o con tendencia y estacionalidad). Estas constantes toman valores entre 1 y 0 y mientras más pequeño sea el valor de la constante, más suavizada estará la observación. Se han desarrollado 3 variantes:

· Alisamiento o suavizamiento exponencial simple o de Brown (para series sin tendencia). En este se usa solamente la constante a para describir el comportamiento medio de la serie.

· Alisamiento exponencial de Holt o con 2 parámetros (para series con tendencia). Se le adiciona la constante b para describir la tendencia.

· Alisamiento exponencial de Winters, de Holt- Winters o con 3 parámetros (para series con tendencia y estacionalidad). Además de a y b, se le adiciona la constante s para describir la estacionalidad).

La decisión de cuál utilizar está relacionada con el tipo de periodicidad que tenga la serie (anual, mensual, semanal, etcétera) y con los componentes que se supone estén o no presentes en la misma.^13,14

Los alisamientos exponenciales requieren de un valor inicial para la primera estimación, así como para las constantes de suavizamiento. El valor inicial de la primera observación puede ser la media de los valores de la serie y para las constantes de suavizamiento, Montgomery y colaboradores recomiendan utilizar valores dentro del intervalo (0,01; 0,3).¹⁵ Otros autores sugieren para obtener el valor óptimo de las constantes, asignarles valores diferentes y comparar la suma de cuadrados residual, pues la mejor opción es la que provea el menor valor para esta suma.^16,17 No obstante, aunque muchos softwares ofrecen la posibilidad de estimar y recomendar el valor óptimo de las constantes de suavizamiento mediante el procedimiento de control adaptativo descrito por Chow,¹⁸ es importante tener en cuenta que los valores pequeños de las constantes de suavizamiento, le dan un peso importante a muchas observaciones anteriores, mientras que los mayores valores le dan más peso a las observaciones recientes de la serie; de hecho, si se ofrece un valor muy cercano a 1 se está aceptando que el valor más reciente es el mejor estimador para los valores futuros, lo que resulta de mucha utilidad en series irregulares.

En la actualidad, estos métodos probablemente constituyan los más utilizados para obtener pronósticos de series temporales cortas debido a su simplicidad, su eficiencia computacional y su aceptable exactitud. En este trabajo se presentan los resultados obtenidos con ambos métodos (ajuste de curvas y alisamientos exponenciales de Holt o con 2 parámetros) en la obtención de pronósticos de la mortalidad por algunas enfermedades no transmisibles seleccionadas, realizados en la Unidad Nacional de Análisis y Tendencias en salud del Ministerio de Salud Pública de Cuba (MINSAP).

 

MÉTODOS

Se realizó un estudio descriptivo de análisis de series temporales correspondiente al período 1970-2006 en Cuba, para obtener una predicción de la mortalidad por algunas causas de muerte en los años 2007-2009. Las fuentes de información empleadas estuvieron constituidas por el conjunto de series cronológicas anuales de mortalidad por las enfermedades no transmisibles seleccionadas (enfermedades del corazón, tumores malignos, enfermedades cerebrovasculares, accidentes, diabetes mellitus, lesiones autoinfligidas intencionalmente) obtenidas de la Dirección Nacional de Estadística (DNE) del MINSAP.

Las características de la información disponible permitieron evaluar la calidad de las series y el aspecto necesario para poder comenzar el proceso de predicción. Se consideró al conjunto de las series como suficientemente consistente para realizar el análisis. Se decidió utilizar las tasas brutas para cada entidad en el período de 1970 a 2006 que se calcularon por cien mil habitantes por cuanto se deseaba obtener un pronóstico del riesgo real de morir en el período 2007-2009.

Dado a que se trataba de datos anuales y se esperaba obtener un pronóstico anual para los próximos 3 años, se utilizó el método del alisamiento exponencial con 2 parámetros el cual se aplicó a todas las series. También se ajustaron varios polinomios y se seleccionó el que tuviera el mayor valor del coeficiente de determinación (R²) y fuera más parsimonioso. Para evaluar la bondad de ajuste de ambos tipos de modelos se compararon los valores obtenidos para el porcentaje de error medio absoluto (PEMA) y se seleccionó el que tuviera menor valor. Se confeccionaron intervalos de predicción para cada valor estimado en el período 2007-2009 con un nivel de confiabilidad de 95 %. El procesamiento estadístico de las series y la obtención de pronósticos se realizó con el software Econometric Views versión 4,0.

 

RESULTADOS

En la tabla 1 se muestran las ecuaciones de los diferentes polinomios definitivamente ajustados a las series de causas de muerte. En todos los modelos el valor del coeficiente de determinación (R²) fue elevado, sobre todo en las series de mortalidad por tumores malignos y lesiones autoinfligidas intencionalmente (0,98 y 0,95, respectivamente). El grado del polinomio fue superior a 2 en todos los casos y la serie de mortalidad por diabetes mellitus requirió de un polinomio de orden 4 para su modelación, el cual a pesar de ser el mejor de todos los ensayados obtuvo el menor valor del R² (0,78) con relación al resto de las series.

En la tabla 2 se aprecia la comparación entre los modelos obtenidos con alisamiento exponencial y con ajuste de polinomios. En todos los casos el porcentaje de error medio absoluto (PEMA) es inferior en los modelos de alisamientos. En el caso de la mortalidad por diabetes mellitus fue notablemente menor (7,25 contra 18,71), mientras que en las series de mortalidad por tumores malignos y lesiones autoinfligidas intencionalmente presentó valores muy similares para ambos.

El buen ajuste de los modelos de alisamientos exponenciales seleccionados se aprecia en las figuras 1, 2, 3, 4, 5 y 6, donde apenas existen diferencias entre los valores reales de las series y los estimados. En varias series se observan retardos entre ambos conjuntos de valores.

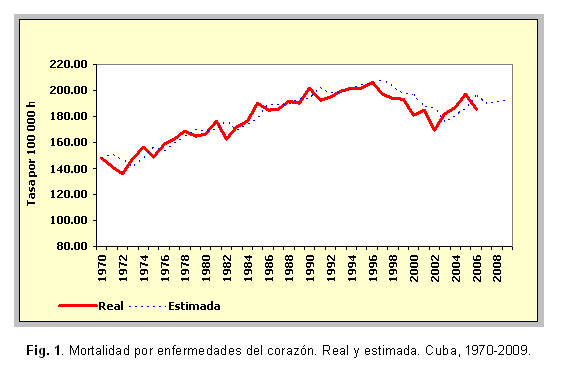
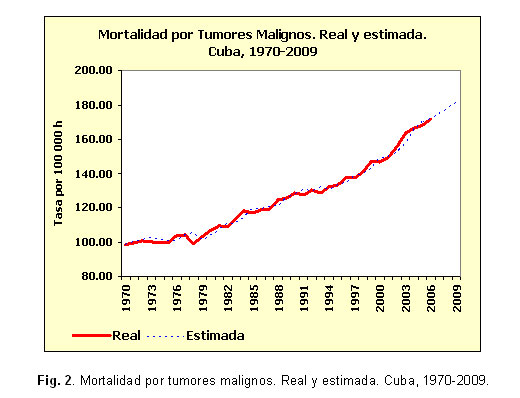
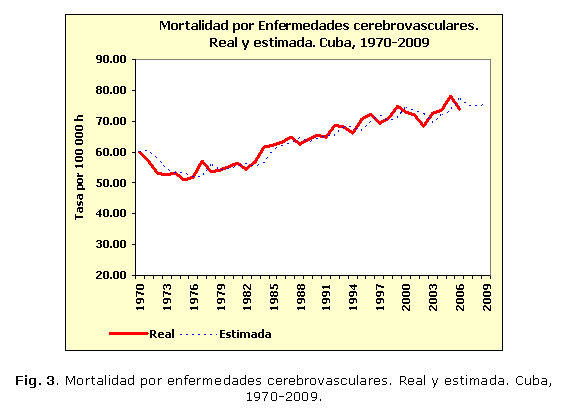
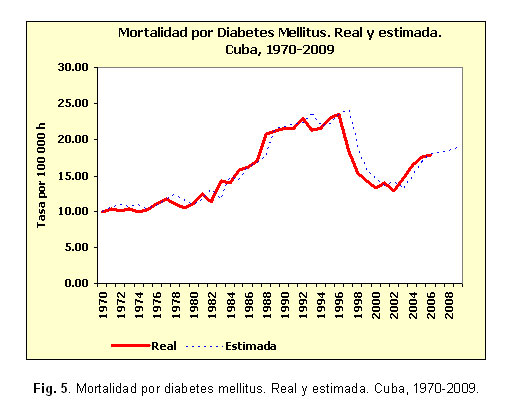
Los valores propuestos para las 2 constantes de suavizamiento involucradas en este modelo (a para la descripción del comportamiento medio y b para describir la tendencia) se observan en la tabla 3. Los mayores valores de la constante a se obtuvieron para las series de mortalidad por diabetes mellitus, lesiones autoinfligidas intencionalmente y tumores malignos. Mientras que los mayores valores de la constante b, se obtuvieron para las series de tumores malignos, enfermedades cerebrovasculares y accidentes. En el caso de la mortalidad por diabetes mellitus la serie exponencial suavizada quedó en función solamente de los valores anteriores de la serie misma puesto que a=1,00 y b=0,00.

Los pronósticos obtenidos, así como los intervalos de predicción para cada serie de mortalidad en el período 2007-2009 se aprecian en la tabla 4. En todos los casos los intervalos fueron bastante estrechos.

 

DISCUSIÓN

La utilización de un número grande de observaciones es según varios autores, una solución razonablemente correcta para el problema que representa la utilización del método de los mínimos cuadrados (MMC) para estimar los parámetros de una recta cuando no se cumple el supuesto de la normalidad, hecho muy frecuente en el ámbito del análisis de series temporales. Sin embargo, no establecen claramente cuán grande tiene que ser este tamaño.^19-21 Otros autores proponen para solucionar este problema, así como el de la heterocedasticidad presente también en las series, la utilización del método de los mínimos cuadrados ponderados.^22,23 En este estudio se consideró que la utilización de 36 años garantizaba el tamaño suficiente para poder utilizar el MMC con suficiente confianza para modelar las series.

El ajuste relativamente bueno obtenido con varios de los polinomios utilizados, dado por los valores elevados del R² y los errores de predicción relativamente pequeños, hubiera bastado para optar por estos para pronosticar el comportamiento anual de la mortalidad en el período 2007-2009, si no se hubieran obtenido algunos modelos poco parsimoniosos, de orden elevado y difíciles de interpretar para varias de las causas de muerte, notablemente para la serie de diabetes mellitus. Esto fue importante para preferir los modelos construidos con los alisamientos máxime cuando con ellos se obtuvieron valores aún menores para los errores de predicción.

Los alisamientos exponenciales constituyen métodos muy simples y la posibilidad de ponderar las observaciones a través de las constantes de suavizamiento le confieren gran poder para la predicción. Sin embargo, tienen algunos inconvenientes y uno de ellos es el retardo que se aprecia en el modelo estimado en la medida en que la tendencia crece o decrece (como en este estudio en la mortalidad por enfermedades del corazón, tumores malignos, diabetes mellitus y accidentes). Otro problema que presenta su utilización surge por la necesidad de actualización constante de los modelos cada vez que se produce una nueva información.²⁴ En este trabajo se considera que ambos inconvenientes no afectaron la buena calidad de los modelos de predicción puesto que la existencia de retardos no impide la interpretación adecuada de los gráficos y en la modelación de series de periodicidad anual las actualizaciones se hacen una vez cada año.

Estos métodos fueron desarrollados para abordar el pronóstico de una gran cantidad de series temporales sin grandes complicaciones y aunque algunos autores plantean que el modelo aditivo de Holt, como el utilizado en este trabajo, resulta más eficiente cuando se han realizado transformaciones previas de los datos (generalmente transformaciones logarítmicas), en este caso se lograron modelos de buena capacidad predictiva sin necesidad de recurrir a las mismas.^25,26

Makridakis y colaboradores señalan que en los alisamientos exponenciales es difícil el cálculo del intervalo de predicción y que deben evaluarse cuidadosamente los métodos que proponen los diferentes softwares en uso pues la no correlación de los errores es crucial para la elaboración de los intervalos;²⁷ mientras que Montgomery considera que si se ha seleccionado un modelo que represente adecuadamente la variación temporal del comportamiento medio del evento, este genera errores que se distribuyen aproximadamente normal y que no están correlacionados, de manera que puede utilizarse un estimador de la varianza del error, en este caso el error cuadrático medio (ECM) para construir intervalos de predicción bastante precisos, como los obtenidos en este estudio.

Una ventaja adicional de la utilización del método de Holt en este trabajo fue el hecho de permitiera poner en evidencia como el comportamiento de una serie exponencial suavizada puede ser expresado en función únicamente de sus propios valores anteriores, como sucedió con la serie de diabetes mellitus, resultados similares obtuvieron Valle y colaboradores en su estimación de modelos de pronósticos.²⁸ Esto resulta particularmente útil por cuanto las series temporales en el ámbito de la vigilancia en salud suelen ser bastante irregulares y difíciles de modelar. La obtención de series estimadas muy similares a las verdaderas, así como un pronóstico completamente coherente con el comportamiento anterior de todas las causas de muerte, unido a los intervalos de predicción estrechos, confirma a juicio de los autores, lo acertado de utilizar alisamientos exponenciales para la obtención de pronósticos anuales.

Se concluye que la vigilancia estratégica adecuada impone la necesidad de perfeccionar las técnicas que permiten la anticipación de modificaciones en el comportamiento de los problemas de salud y la preparación de planes de contingencia con limitada incertidumbre. Ofrecer pronósticos, que brinden cierto grado de confianza, acerca de la evolución futura de las causas de muerte en un horizonte de tiempo determinado contribuye a lograr una mejor preparación del sistema de salud para su enfrentamiento.

Además, la utilización de modelos de predicción de relativamente fácil construcción como los obtenidos con alisamientos exponenciales en este estudio, pueden resultar muy útiles para la vigilancia de eventos de salud diversos ya que permiten a las autoridades sanitarias el conocimiento previo que facilita en gran medida la toma de decisiones oportunas.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Rodríguez D. La práctica de la vigilancia en Cuba. [Consultado 9 de octubre de 2007]. Disponible en URL: http://bvs.sld.cu/uats/articulos_files/uats.pdf

2. Murillo C, Antó J. Métodos estadísticos de series temporales. Aplicaciones sanitarias. Barcelona: SG editors; 1998. p. 58-67.

3. Chatfield C. The análisis of time series. An introduction. Sixth Edition. USA: Chapman & Halll/CRC; 2004. p. 16-7.

4. Coutin G. El tiempo y el espacio en el análisis de situación de salud. Capítulo 4: En el Libro de Silvia Martínez Calvo: El análisis de la situación de salud. La Habana: Editorial Ciencias Médicas; 2005. p. 56-60.

5. Sánchez M. La demanda residencial de energía eléctrica en la comunidad autónoma de Andalucía: Un análisis cuantitativo. [Consultado 9 de octubre de 2007]. Disponible en URL: http://descargas.cervantesvirtual.com/servlet/SirveObras/01604185214584961880035/013293_13.pdf

6. Chatfield C. The análisis of time series. An Introduction. Sixt Edition. USA: Chapman & Halll/CRC; 2004. p. 90-5.

7. Parisi A. Técnicas de evaluación de modelos. [Consultado 9 de octubre de 2007]. Disponible en URL: http://parisinet.com/Cs/Cds/FINANZAS/cap7/7-4/texto7-4.htm

8. Aragon Y. Introduction aux series témporelles. Septembre 2002. [Consultado 9 de octubre de 2007]. Disponible en URL: http://w3.univ-tlse1.fr/GREMAQ/Statistique/Yvesweb/docs/IUP_st_cours.pdf

9. Chevillon G. Pratique de series temporelles. France 2004. [Consultado 9 de octubre de 2007]. Disponible en URL: http://guillaume.chevillon.free.fr/lecturenotes.pdf

10. Diggle P. Time series. A biostatistical introduction. United Kingdom: Oxfor Univesity Press; 2000. p. 21-7.

11. Pindyck R, Rubinfeld D. Econometric models and econometric forecasts. Fourth Edition. Chapter 6. Serial correlation and heteroscedasticity. New York: Wiley and sons; 1998. p. 135-40.

12. Wei W. Time series analysis: univariate and multivariate methods. Canada: Addison Wesley Publishing Company; 1994. p. 148-50.

13. Mc Nally R. Forecasting expenses related to SBLA and CBSFA Lending. [Consultado 10 de enero de 2007]. Disponible en URL: http://strategis.ic.gc.ca/internet/incsbfp-pfpec.nsf/en/la0028e.html

14. Davies C. Engineering statistics handbook. Exponential smoothing summary. [Consultado 12 de mayo de 2007]. Disponible en URL: www.itl.nist.gov/div898/handbook/mpc/section7/mpc7.html

15. Montgomery DC, Johnson LA, Gardiner JS. Forecasting and time series analysis. Second edition. New York: Mc Graw Hill; 1994. p. 83-7.

16. Brown RG. Smothing, forecasting and prediction of discrete time series. New Jersey: Prentice Hall; 1962.

17. Winters PR. Forecasting sales by exponentially weigthed moving averages. Man Sc.1960;6(3):324-42.

18. Chow WM. Adaptative control of the exponential smoothing constant. JIE. 1965;16(5):314-7.

19. Pindyck R, Rubinfeld D. Econometric models and econometric forecasts. Fourth Edition. Chapter 6. Serial Correlation and Heteroscedasticity. New York: Wiley and sons; 1998. p. 145-51.

20. Hamilton JD. Time series analysis. New York: Princeton University Press; 1994. p. 207-23.

21. Montgomery DC, Johnson LA, Gardiner JS. Forecasting and time series analysis. Second Edition. New York: Mc Graw Hill; 1994. p. 181-5.

22. Cameron CA, Triverdi PK. Microeconometrics: methods and applications. New York: Cambridge University Press; 2005. p. 77-83.

23. Aguirre Jaime A. Introducción al tratamiento de series temporales. Aplicación a las ciencias de la salud. Madrid: Díaz de Santos; 1994. p, 547-8.

24. Wei W. Time series analysis: univariate and multivariate Methods. Canada: Addison Wesley Publishing Company; 1994. 150-4.

25. Bermúdez J, Corberán A, Vercher E. Selección de transformaciones en la predicción de series temporales con el modelo de Holt. [Consultado 13 de octubre de 2007]. Disponible en URL: http://www.seio2006.ull.es/files/43/resumen_43_QlXLQafqfI.pdf

26. Hyndman RJ, Koehler AB, Zinder RD, Grose S. A state space framework for automatic use of exponential smoothing methods. International Journal of Forecasting. 2002;18:439-54.

27. Makridakis S, Wheelwrigth S; Hyndman RJ. Forecasting: methods and applications. Thitr edition. USA: Jonh Wiley and sons; 1998. p. 177-8.

28. Valle HA, Morán HE. Estimación y evaluación de modelos alternativos de pronósticos de inflación en Guatemala. CEMLA. VIII Reunión de la red de Investigadores de Bancos Centrales del continente americano. [Consultado 13 de octubre de 2007]. Disponible en URL: http://www.banguat.gob.gt/publica/doctos/bgdocto017.pdf

 

 

Recibido: 27 de mayo de 2008.
Aprobado: 18 de noviembre de 2008.

 

 

Gisele Coutin Marie. Unidad Nacional de Análisis y Tendencias en Salud Nacional/ Ministerio de Salud Pública, La Habana, Cuba. E-mail: [e-mail]