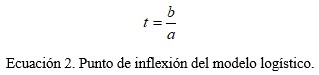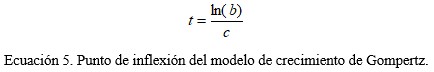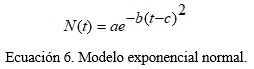Introducción
Una situación muy difícil con la salud se presenta en el planeta actualmente. La Organización Mundial de la Salud declara el 11 de marzo del 2020 la pandemia de la COVID-19 y plantea una serie de medidas para evitar el contagio entre las personas; el aislamiento se plantea como condición esencial así como el mantenimiento de una conducta de autorresponsabilidad, instando a la imposición de medidas sanitarias por los gobiernos de cada país.
En principios del mes de marzo del 2020 en Cuba se presentan las primeras manifestaciones de la COVID-19, y la dirección de país plantea medidas de cuarenta para enfrentarlo, algunas de ellas fueron: evitar concentraciones de personas, cerrar temporalmente las actividades en las universidades e implementar modalidades a distancias, que contribuyan a la formación de los profesionales, utilizando modalidades no presenciales y que los profesores se dediquen al desarrollo de las medios de enseñanza, el trabajo científico y las publicaciones.
Los científicos en el mundo comenzaron a trabajar en la modelación matemática de la epidemia provocada por el nuevo coronavirus SARS.CoV.2 causante de la COVID-19, utilizando diversas técnicas y modelos matemáticos. Han sido utilizadas diferentes vías para dicha modelación matemática:
Modelación clásica para las epidemias con modelos SIR basados en ecuaciones diferenciales ordinarias. Investigaciones en este sentido para la pandemia han sido:1,2,3
Modelación de la Covid-19 basadas en modelos estadísticos de series cronológicas.4
Modelos predictivos a través del uso de internet.5
Modelos basados en inteligencia artificial y Machine Learning.6,7
Las modelaciones antes expuestas tienen presente una serie de parámetros que permiten la inclusión de varios factores con el fin de expresar, lo mejor posible, las realidades de las epidemias, sin embargo, presentan alto grado de complejidad y nivel de procesamiento para la obtención de estos parámetros.
Dentro de los modelos estadísticos se encuentran los de ajuste de crecimiento poblacional logísticos y exponenciales (modelos de crecimiento de Gompertz). En algunas publicaciones se encuentra la utilización con éxito de estos en la epidemia de la Covid-19. Algunas publicaciones lo han hecho,8,9,10 y presentan una complejidad inferior a las modelaciones antes expuestas.
El objetivo fundamental del presente trabajo es obtener predicciones para el pico de casos confirmados y fallecidos en Cuba, haciendo uso de herramientas estadísticas e informáticas.
Métodos
El método de los mínimos cuadrados fue utilizado para la obtención de los parámetros de los modelos utilizando modelos lineales (MCL) y no lineales (MCNL).
Los modelos logísticos, como la curva de crecimiento logístico11 utilizada para modelar el crecimientos poblacional puede ser utilizada en el pronóstico del crecimiento de casos infectados y/o decesos respectivamente.
Un modelo básico logístico tiene la siguiente expresión (Ecuación 1):
Este modelo puede ser utilizado para el pronóstico de las epidemias teniendo presente que P(t) representa los casos acumulados (casos confirmados o fallecimientos), t representa el tiempo trascurrido luego de haberse presentados los primeros casos y a y b son parámetros que pueden ser obtenidos (luego de realizar transformaciones matemáticas) aplicando el método de los MCL. Para la utilización de este modelo los datos deben ser llevados a la escala de [0; 1] dividiendo cada dato entre el mayor obtenido. En este modelo un valor importante lo representa el punto de inflexión debido a que muestra el cambio de comportamiento de la curva lo cual puede ser interpretado como el pico de la epidemia. Este punto de inflexión está dado por la expresión (Ecuación 2):
Una modelación que ofrece mayor versatilidad, está representada en la Ecuación 3. En este caso no es necesaria la transformación de los datos a la escala de [0; 1], dado que el parámetro c representa el máximo de casos acumulados y el punto de inflexión es el mismo que el presentado anteriormente. Sin embargo, presenta un mayor nivel de complejidad para la obtención de los parámetros debido a que no es posible, mediante transformaciones matemáticas, obtener un modelo lineal con respecto a los parámetros por lo que se aplica el método de los MCNL para la obtención de los mismos.11
Modelos exponenciales, la curva de crecimiento exponencial de Gompertz11 pertenecen a la familia de curvas sigmoideas, inicialmente cóncavas y tras pasar el punto de inflexión, convexas. Su nombre procede del matemático Benjamin Gompertz, el cual utiliza la curva para describir la ley de la naturaleza que rige la mortalidad humana. Existen diferentes tipos de curvas Gompertz en función de les parámetros que la componen, sin embargo, están caracterizadas por una doble exponencial como elemento característico común. (Ecuación 4)
En este modelo G(t) representa los casos acumulados (casos confirmados o fallecimientos), t representa el tiempo trascurrido luego de haberse presentados los primeros casos y a, b y c son parámetros que pueden ser obtenido aplicando el método de los MCNL. El punto de inflexión está dado por la expresión (Ecuación 5):
Los modelos anteriores presentan estabilidad debido a que utilizan los valores acumulados de los casos, sin embargo, su representación geométrica, en ocasiones, limita su comprensión. Un modelo, de fácil interpretación geométrica, que puede ser utilizado para la representación de los casos por cada día, es el modelo exponencial basado en los modelos normales (Ecuación 6):
En este modelo N(t) representa los casos obtenidos por días (casos confirmados o fallecimientos), t representa el tiempo trascurrido luego de haberse presentados los primeros casos y a, b y c son parámetros que pueden ser obtenidos (luego de realizar transformaciones matemáticas) aplicando el método de los MCL. En este modelo es de gran importancia el punto estacionario que muestra el cambio de comportamiento de la curva que pasa de un crecimiento a un decrecimiento. Este punto está dado por la expresión t=c.
Para la bondad del ajuste de los modelos se utiliza el coeficiente de determinación ajustado R2, adecuado para modelos no lineales con respecto a los parámetros.
En la presente investigación se pretende realizar pronósticos de las fechas para el pico de casos confirmados y casos fallecidos por la enfermedad COVID-19 respectivamente para Cuba, así como el total de casos confirmados y fallecidos pronosticados.
Los datos utilizados para la estimación de los modelos son tomados del sitio web www.cubadebate.cu con la información diaria y acumulada en Cuba. Estos datos se encuentran actualizados hasta la fecha de escrito este informe, 22 de abril de 2020.
Para la aplicación de la metodología es importante la selección del primer día de conteo de datos. Se comenzó a contabilizar el primer día de aparición de casos para los datos confirmados diarios y acumulados y el primer día de fallecimiento de una persona por esta enfermedad para los datos de decesos diarios y acumulados.
Para el procesamiento de la información se utilizaron los programas informáticos Maxima 5.41.012 y R 3.6.113. Para el procesamiento de los modelos que utilizaron el método de los MCL se empleó el programa simbólico Maxima y para el procesamiento de los modelos utilizando el método de MCNL se empleó el lenguaje de programación R, de procesamiento numérico.14 En ambos casos se implementaron una serie de instrucciones que permiten el análisis, de forma rápida, de cualquier país afectado por la COVID-19 existente en la base de datos. Ambos ficheros de instrucciones (covid_19.mac para el caso de Maxima y covid_19.R para el caso de R) pueden ser descargados desde la dirección https://clasesvirtuales.ucf.edu.cu/course/view.php?id=1147. Para la utilización del método de los mínimos cuadrados se utilizó el paquete lsquare.mac en el programa Maxima y las instrucciones nls, SSlogis y SSgompertz del paquete stat de R.
Resultados
Estimaciones para la información de casos confirmados en Cuba.
Cuba presentó sus primeros casos el 11 de marzo, pero se registraron a partir del día posterior (12 de marzo). Al momento de escrito este informe investigativo habían transcurrido 42 días desde el primer reporte. (Tabla 1)
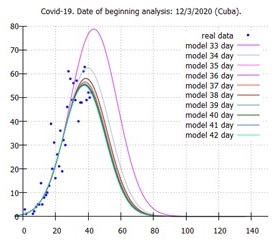
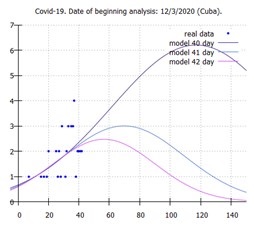
El gráfico que se muestra en la figura 1 expone las representaciones geométricas de los casos confirmados por días y diez modelos exponenciales (ecuación 6). Cada modelo representa la estimación obtenida para cada uno de los días de avance de la enfermedad a partir de pasado 33 días de inicio de la misma (13 de abril) hasta pasado 42 días (22 de abril). Estos modelos presentan estabilidad a partir de pasado 35 días de inicio de la enfermedad (15 de abril), un pico estimado pasado entre 38 (18 de abril) y 39 (19 de abril) días y coeficientes de determinación que oscilan entre 0,87 y 0,88.
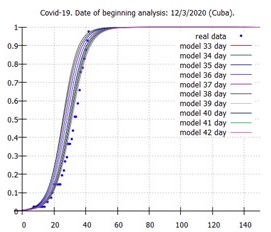
La figura 2 muestra la representación geométrica de los casos confirmados acumulados, llevados a la escala de [0,1] y diez modelos logísticos (ecuación 1). De igual forma estos modelos presentan estabilidad, un pico estimado pasado entre 24 (4 de abril) y 28 (8 de abril) días luego de confirmados los primeros casos en el país (12 de marzo) y R2 que oscilan entre 0,88 y 0,97.
La figura 3 muestra la representación geométrica de los casos confirmados acumulados y la del modelo logístico (ecuación 3). En este modelo se estima el pico pasado 34 días (14 de abril) luego de confirmados los primeros casos en el país (12 de marzo) y un R2 adecuado aproximadamente igual a 0,99865.
La figura 4 muestra la representación geométrica de los casos confirmados acumulados y la del modelo de crecimiento exponencial de Gompertz (ecuación 4). En este modelo se estima el pico pasado 39 días (19 de abril) luego de confirmados los primeros casos en el país (12 de marzo) y un R2 muy adecuado aproximadamente igual a 0,99936.

Fig. 4 - Modelos de crecimiento exponencial de Gompertz. Casos confirmados acumulados en Cuba. (Tomado de R)
A continuación, se presenta una comparación de las estimaciones realizadas mediante los modelos. (Tabla 2).
Los modelos logístico y de Gompertz presentan mejor bondad de ajuste dado que sus R2 son muy adecuados. A través de estos modelos se estima un pico de casos contagiados pasado entre 34 días (14 de abril) y 39 días (19 de abril) (a la fecha de escrito este informe se estima ya pasado el pico), luego de confirmados los primeros casos en el país (12 de marzo). Se pronostican, además, un total de contagiados con la COVID-19 entre 1482 a 2678.
Estimaciones para la información de casos fallecidos en Cuba.
Cuba presentó su primer caso de deceso el 18 de marzo. Al momento de escrito este informe investigativo han transcurrido 36 días desde este fallecimiento.
El gráfico que se muestra en la figura 5 expone las representaciones geométricas de los casos fallecidos por días y tres modelos exponenciales (ecuación 6). Cada modelo representa la estimación obtenida para cada uno de los días de avance de la enfermedad a partir de pasado 40 días (20 de abril) hasta 42 días (22 de abril) desde que se presentaron los primeros casos confirmados en el país. Estos modelos presentan inestabilidad y coeficientes de determinación bajos (entre 0.23 y 0.24), por lo que se pone de manifiesto que son poco adecuados para utilizarlo como predictores.
La figura 6 muestra la representación geométrica de los casos fallecidos acumulados, llevados a la escala de [0,1] y diez modelos logísticos (ecuación 1). Estos modelos presentan una estabilidad media, un pico estimado pasado entre 26 (6 de abril) y 32 (12 de abril) días luego de confirmados los primeros casos en el país (12 de marzo) y R2 que oscilan entre 0,79 y 0,98.
La figura 7 muestra la representación geométrica de los casos fallecidos acumulados y la del modelo logístico (ecuación 3). En este modelo se estima el pico pasado 32 días (18 de abril) luego de haber fallecido el primer caso en el país (18 de marzo) y un R2 adecuado aproximadamente igual a 0,99656.
La figura 8 muestra la representación geométrica de los casos confirmados acumulados y la del modelo de crecimiento exponencial de Gompertz (ecuación 4). En este modelo se estima el pico pasado 49 días (5 de mayo) luego de haber fallecido el primer caso en el país (18 de marzo) y un R2 adecuado aproximadamente igual a 0,99582.
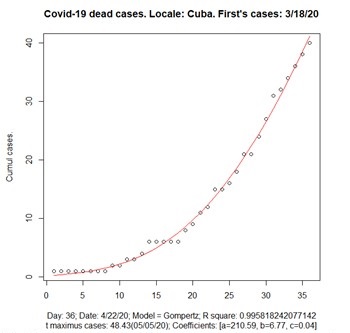
Fig. 8 - Modelos de crecimiento exponencial de Gompertz. Casos fallecidos acumulados en Cuba. (Tomado de R)
A continuación, se presenta una comparación de las estimaciones realizadas mediante los modelos (Tabla 3).
Los modelos logísticos y de Gompertz presentan mejor bondad de ajuste dado que sus R2 son adecuados. A través de estos modelos se estima un pico de casos fallecidos pasado entre 32 días (18 de abril) y 49 días (5 de abril) luego de que falleciera el primer caso en el país (18 de marzo). Se pronostican, además, un total de fallecidos por la COVID-19 entre 63 a 211.
Discusión
En el presente artículo de investigación se expusieron predicciones para los picos de casos confirmados y decesos en Cuba respectivamente, asociados a la COVID-19, así como las afectaciones en cantidad total de personas contagiadas y fallecidas.
Han sido utilizados modelos logísticos y exponenciales (específicamente el modelo de crecimiento de Gompertz) para obtener estas estimaciones. Estos modelos han sido contrastados, con resultados satisfactorios, con los datos publicados, por las afectaciones de esta enfermedad.
Cuba comienza a ser afectada por la pandemia COVID-19 alrededor de 20 días después de haber sido afectados Italia y España, lo cual le dio un margen de preparación basado en las experiencias de países como China, Corea del Sur y las propias Italia y España.
Se han obtenido las conclusiones siguientes:
Los modelos estadísticos de predicciones obtenidos dan resultados muy significativos para el estudio de la pandemia COVID.19 en Cuba.
El pico estimado de contagiados se debe haber alcanzado (con respecto a la fecha en que se ha escrito este informe de investigación 22 de abril), en un estimado aproximadamente, entre el 14 y 19 de abril, pronosticándose una cantidad total de contagios entre 1 482 y 2 678. Sin embargo, el pico de fallecidos se pronostica que debe alcanzarse entre el 18 de abril y 5 de mayo y se estima una cantidad total de deseos en un rango entre 63 y 211.
El sistema de salud cubano ha demostrado su solidez y efectividad diferente al que presentan otros países contagiados en el mundo y la certera política por parte del sistema de salud y el gobierno para tratar la posible epidemia es también distinta.