Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Energética
versión On-line ISSN 1815-5901
Energética vol.34 no.1 La Habana ene.-abr. 2013
APLICACIÓN DE LACOMPUTACIÓN
Efectividad del método de flujo con recurrencia en estudios en ciruitos de distribución primaria
Efectivity of the recurrect flux method in primary distribution studies
Dr. Raúl Nicolás Carvajal Pérez, Héctor Silvio Llamo Laborí
Centro de Investigaciones y Pruebas Electroenergéticas, CIPEL, Instituto Superior Politécnico José Antonio Echeverría Cujae, La Habana, Cuba.
RESUMEN
Los estudios de circuitos de distribución comienzan con el cálculo de flujo de potencia por el circuito. Este refleja su estado actual en cuanto a pérdidas y caídas de tensión; básicos para cualquier análisis. Cuando se trabaja con técnicas genéticas, estos cálculos se realizan miles de veces. En este trabajo se sugiere un método de cálculo de flujo de potencia en circuitos de distribución radiales. Se aplica éste cuando solo se conoce la demanda total del circuito utilizando "Ardvinson" para asignar una "demanda de cálculo" a cada nodo. En esencia se realiza una primera iteración utilizando esa demanda y la tensión nominal del circuito en una dirección. La segunda iteración recurre a los valores obtenidos en la primera. Se exponen los cálculos realizados en un circuito real utilizando un sistema de cálculo específico y el Microsoft EXCEL para demostrar la rapidez del método y su nivel de exactitud.
Palabras clave: circuitos primarios, estudios de flujo, flujo de potencia.
ABSTRACT
The first step in Distribution Circuits studios consist in power flux calculus. It shows the actual situation. of the circuit. When the studio is realized using genetic techniques, this step is repeated thousands times. A method to obtain power flux in distribution circuits is presented. The method is applied when only have the total circuit demand. Here is applied Ardvinson method to obtain "Calculus demand" in each node, realize the first iteration with these demand and nominal tension. Later, repeat the calculus using the values obtained before. An example of real circuit is resolved using specific software and EXCEL to demonstrate the efficiency of the method.
Key Words: primary circuits, flux studies, power flux.
INTRODUCCIÓN
Los estudios de circuitos de distribución primaria comienzan por el cálculo de flujo de potencia. Este es la base para los análisis del estado actual del circuito y la evaluación de mejoras. La confiabilidad en los resultados del cálculo de flujo es importante pero también lo es la rapidez del método utilizado cuando se tienen que realizar estos cálculos repetidamente. Aspectos importantes de estos estudios son la compensación de reactivo o la reconfiguración de la red que generalmente utilizan técnicasgenéticas.
En ellos hay que realizar cálculos de flujo de potencia miles de veces y la tendencia ha sido utilizar las técnicas de Newton Raphson [1-3]. Esta técnica consume mucho tiempo de cálculo y en los últimos años, algunos autores [4-5], han desarrollado métodos híbridos tratando de disminuir la cantidad de variantes que se evalúan.
Otra forma de abordar el problema del volumen de cálculo necesario hasta llegar al entorno del óptimo es la de reducir el tiempo de cálculo en cada variante. El objetivo de este trabajo es mostrar la efectividad y rapidez en el cálculo de flujo de potencia en redes radiales a partir de la utilización del método aproximado de la matriz topológica para obtener valores iniciales y recalcular el flujo utilizando estos valores; es decir, por recurrencia.
DEMANDA DE LOS NODOS Y POTENCIA CIRCULANDO POR LA RED
La información básica para el estudio de un circuito comprende: las potencias que circulan por las líneas, pérdidas de potencia y energía y caídas de tensión en los elementos de la red.
Frecuentemente, en el estudio de un circuito de distribución primaria, no se cuenta con los datos de demanda máxima, tensión, factor de carga y factor de potencia de los nodos del circuito; solo se tienen los datos de la curva típica de la subestación y en algunos casos de los principales nodos del circuito [6-7]. Es importante definir hasta qué punto es confiable trabajar a partir de esta información utilizando un método aproximado.
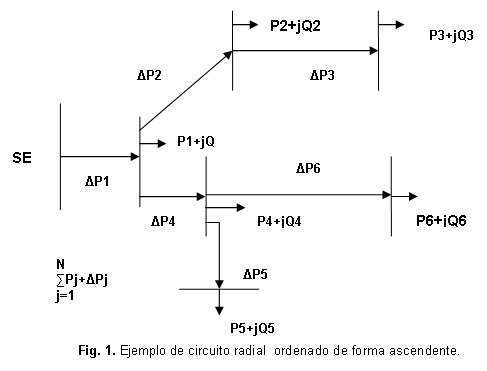
En la figura 1, se muestra un pequeño circuito que servirá de apoyo en el análisis. Se ha seguido la práctica conveniente de utilizar una numeración secundaria o de cálculo consistente en numerar los nodos por enteros continuos cumpliendo la condición siguiente: si el nodo i envía energía al nodo j; entonces i<j.
En este circuito radial, se observan diferencias entre la potencia de envío y recibo de cada tramo. Si las pérdidas en el tramo al nodo i son Δpi, entonces la potencia de envío del nodo:
![]()
Donde: Pr(i), Qr(i) son las potencias de recibo del tramo al nodo i.
En los nodos más alejados de la subestación SE, los valores de las pérdidas asociadas al tramo de alimentación (i) Δpi, Δqi normalmente son más pequeños que en los ramales que se encuentran más próximos a la subestación. El cálculo de las pérdidas de cada tramo se realiza con las potencias y tensiones del recibo de este.
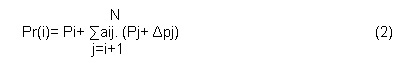

Aquí:
aij es el coeficiente de la matriz topológica que relaciona ambos nodos i y j.
La nomenclatura utilizada permite realizar la secuencia de cálculos con facilidad si se comienza desde el nodo N hacia la subestación dado que la matriz topológica es una matriz "booleana" y triangular.
Características de los circuitos de distribución primaria
Con excepción de algunos circuitos aislados, los circuitos de distribución del país, operan de forma radial y prestan servicio a tensiones entre 4,16 kV y 13,8 kV. La cantidad de servicios que prestan oscila entre 50 y 350 puntos de alimentación (Nodos). La mayoría de los usuarios de un circuito cuentan con equipos de medición de energía; solo algunos de ellos, por su importancia, tienen instalaciones adicionales. Estas condiciones obligarían a los especialistas en distribución a realizar un amplio trabajo de medición que permita obtener los datos de demanda, tensión, factor de carga y factor de potencia en cada nodo; medidos simultáneamente o en condiciones tales que haya congruencia entre las medidas realizadas a todos los nodos logrando que éstas sean compatibles con las mediciones en la subestación.
Análisis de los resultados de aplicar el método de Ardvinson
Suponga que en un circuito de distribución primaria con N nodos, existen N1 de ellos con la posibilidad o necesidad de realizar mediciones de los parámetros requeridos en el cálculo del flujo de potencia. (Llamados nodos "leídos"). Si a la demanda de la subestación se le resta el acumulado de esa demanda "leída", quedará una demanda S(t) que corresponde a la de los demás nodos más las pérdidas del circuito. En el momento de máxima demanda, sea Smax= S(t). El método de "Ardvinson" asigna una potencia de cálculo a cada nodo de acuerdo con la capacidad instalada (kVAinst). Para esto, calcula un factor de capacidad (Fcap) que es la relación entre la demanda de los nodos "no leídos" y la capacidad de transformación total de esos nodos. Fcap= (Smax /kVAinst)
También asume que el factor de carga y factor de potencia de estos nodos es uniforme e igual al del conjunto de los nodos "no leídos" Esta potencia asignada incluye la demanda del nodo y un aporte para tener en cuenta las pérdidas del circuito. El factor de capacidad se calcula sin tener en cuenta el efecto de los condensadores instalados.
Las suposiciones del método de Ardvinson no son confiables para la evaluación de la demanda de un nodo de forma aislada; sino para tener en cuenta el efecto del nodo en la evaluación del circuito en su conjunto. De esta forma, los nodos más alejados pueden dar resultados que difieren sensiblemente de los obtenidos por Ardvinson pero el conjunto ofrece mayor fiabilidad.
Para realizar un análisis más detallado se utilizará un circuito real. La figura 2, muestra un circuito de 53 nodos que fue estudiado utilizando el método de Ardvinson.
Los resultados de una primera iteración en el cálculo de flujo de potencia se muestran en las figuras 3 y 3(a). Las pérdidas totales de potencia activa son de 114 kW en el estado actual. En la figura aparecen los detalles de cálculo por tramos del circuito.
De acuerdo con la topología del circuito mostrada en la figura 2, hay tramos y ramales en los que la potencia de envío calculada ofrece gran confiabilidad y otros que no. Los tramos más confiables son:
Tramo Ptramo ( kW.) Perdidas (kW.) Observación
0-1 2305 13,02 Es exacto. Sale la potencia medida en la SE
1-2 2295 4,50 Incluye 52 de los 53 nodos del circuito.
2-4 2152 2,18 Incluye 51 nodos del circuito
4-5 2152 1,32 Incluye 50 nodos del circuito
5-6 2152 4,28 Incluye 49 nodos del circuito
6-7 363 0,48 Incluye 13 nodos del circuito
6-20 1789 7,61 Incluye 43 nodos del circuito
20-21 1747 1,55 Incluye 42 nodos del circuito
21-22 1711 6,57 Incluye 41 nodos del circuito
22-23 1711 2,52 Incluye 40 nodos del circuito
23-24 1665 7,94 Incluye 39 nodos del circuito
24-25 1610 8,97 Incluye 38 nodos del circuito
25-26 1527 11,84 Incluye 37 nodos del circuito
26-29 1469 7,58 Incluye 34 nodos del circuito
29-30 1432 2,20 Incluye 33 nodos del circuito
30-31 1395 10,20 Incluye 32 nodos del circuito
Estos 16 tramos representan solo el 30 % del total del circuito y acumulan 92,76 kW de pérdidas de potencia activa que representan el 81 % del total. Los restantes tramos (70% de los tramos) solo aportan el 19 % de las pérdidas totales.
Los tramos que no se han incluido como confiables individualmente, ofrecen como grupo una confiabilidad aceptable puesto que la potencia total de ellos se corresponde con el total asignado. Individualmente hay valores en exceso que son compensados por la potencia asignada a otros nodos en defecto y por tanto habrá un nivel de compensación de errores en los cálculos posteriores aunque este no se determine cuantitativamente.
AFECTACIONES POR CAÍDAS DE TENSIÓN FIJAS
En el cálculo de pérdidas y caídas de tensión por el método de la matriz topológica, se consideró la potencia de recibo de cada tramo que alimenta a un nodo y la tensión nominal del circuito sin tener en cuenta las caídas de tensión desde la subestación al nodo correspondiente. Si se considera el paso anterior como una primera iteración y se realiza una segunda iteración, tomando los valores de potencia y tensión de recibo obtenidas en cada nodo en esa primera iteración, como valores iniciales, se observan notables diferencias en los tramos más importantes (que transportan la mayor cantidad de potencia). Las pérdidas son mayores que en la primera iteración. En la tabla 1, aparece el cálculo inicial utilizando la matriz topológica para el circuito en estudio utilizando los sistemas "Edis" y en la tabla 2, se muestran los cálculos manuales utilizando el Microsoft "EXCEL". Se nuestra el cálculo inicial, la primera iteración con las potencias de cálculo y las potencias que se utilizan en la siguiente iteración. En esa tabla se puede apreciar que la primera iteración difiere de la segunda cerca de un 8 % pero ya la siguiente iteración no mejora prácticamente los resultados. Estos resultados tienen comportamiento similar en la generalidad de los circuitos de distribución primaria.
En la tabla 2, se muestran los cálculos manuales utilizando el Microsoft "EXCEL". Se nuestra el cálculo inicial, la primera iteración con las potencias de cálculo y las potencias que se utilizan en la siguiente iteración. En esa tabla se puede apreciar que la primera iteración difiere de la segunda cerca de un 8 % pero ya la siguiente iteración no mejora prácticamente los resultados. Estos resultados tienen comportamiento similar en la generalidad de los circuitos de distribución primaria.
Importancia de la cantidad de iteraciones en el cálculo de flujo en un estudio
La cantidad de iteraciones tiene notable importancia cuando es necesario realizar cálculos de flujo varias veces en el estudio de distribución. Los casos más frecuentes son: la optimización de la compensación de reactivo y la reconfiguración de la red utilizando técnicas genéticos como se explicó en la introducción. En estos estudios se generan miles de individuos que representan variantes de redes y para cada uno de ellos se realiza el cálculo de flujo de potencia puesto que cada individuo generado tiene una topología diferente o localización y tamaño de banco diferentes según el caso.
CONCLUSIONES
La compensación óptima de reactivo en un circuito de distribución utilizando técnicas genéticas obliga al cálculo del flujo de potencia de cada uno de los miles de individuos que se generan . Es conveniente utilizar métodos de cálculo que consuman el menor tiempo de cómputo posible con resultados confiables. El cálculo de flujo de potencia utilizando el método de flujo con recurrencia, ofrece resultados rápidos y confiables en general. Se ha podido comprobar que a partir de la segunda iteración, los resultados prácticamente no difieren de la iteración anterior. Este es útil en la realización de estudios de optimización del reactivo de redes de distribución utilizando técnicas genéticas.
REFERENCIAS
1. Edgar M., "Um algoritmo genético modificado no problema de minimizacao de perdas activas em redes de distribucao de energia". XIV Congreso brasileiro de automática. Brasil, 2004.
2. Wan Lou Shin. "Demonstrating an efficient capacitor location and sizing method for distribution system application to the Macau network". Macau Electric company INESC. Porto. Portugal: INESC Porto - Instituto de Engenharia de Sistemas e Computadores do Porto, 2005, [consulta: mayo 2012], Disponible en: http://power.inescn.pt/Portugal.
3. Leiva, M.A., "Localización óptima de condensadores en un sistema de distribución vía algoritmos genéticos". (Tesis de grado), Universidad de Santiago de Chile, 2001
4. Miranda, V., "A general methodology for distribution planning under incertainly, including genetic algorithm and fuzzy models in a multicriteria environment". INESC. Porto. Portugal: INESC Porto - Instituto de Engenharia de Sistemas e Computadores do Porto, 2005, [consulta: mayo 2012], Disponible en: http://power.inescn.pt/Portugal.
5. Miranda, V., "Experimenting in the optimal capacitor placement and control problem with hybrid mathematical- Genetic Algorithm". INESC. Porto. Portugal: INESC Porto - Instituto de Engenharia de Sistemas e Computadores do Porto, 2004, [consulta: mayo 2012], Disponible: http://power.inescn.pt/Portugal.
6. Y., Huang; H., Yang, "Solving the Capacitor Problem in a Radial Distribution System using Tabu Search Aproach". IEEE Trans. On Power System, November 1996, vol.11, n.4, p. 1868-1873.
7. M., Delfani; et al., "Optimal Capacitor Placement usin Deterministic and Genetic Algorithm". IEEE Trans. On Power System, August 2000, vol.15, n.3, p. 1041-1046.
Recibido: Octubre del 2012
Aprobado: Enero del 2013
Dr. Raúl Nicolás Carvajal Pérez, Ingeniero Electricista, Profesor Titular, Dr. en Ciencias Técnicas, Centro de Investigaciones y Pruebas Electroenergéticas, CIPEL, Instituto Superior Politécnico José Antonio Echeverría,Cujae, La Habana, Cuba. email: rncp@electrica.cujae.edu.cu