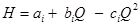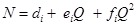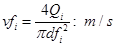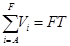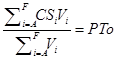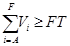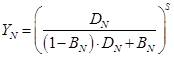Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
En las aplicaciones industriales se estima que solamente en el accionamiento de bombas, ventiladores, compresores y aplicaciones de tracción mecánica, los motores de inducción consumen cerca del 70% de la energía eléctrica utilizada. En las industrias químicas y del petróleo los accionamientos de bombas pueden superar el 50% del consumo de energía eléctrica [1]. En las industrias que procesan el mineral laterítico cubano, los sistemas de transporte de fluidos son consumidores de una parte importante de la energía utilizada con fines productivos.
Según [2, 3, 4], más del 60% de la energía total que se consume en la transportación de fluidos ocurre mediante los accionamientos eléctricos con motores de inducción, y de este consumo, más del 55% se utiliza en los accionamientos de bombas. La eficiencia energética de las bombas utilizadas en el transporte de hidromezclas laterítica depende considerablemente de las características reológicas del fluido trasegado; sin embargo, dado el insuficiente conocimiento disponible de estas características, la selección y explotación de las mismas se ha realizado históricamente bajo el supuesto de que el comportamiento reológico de los fluidos es newtoniano [5, 6, 7]. Es evidente, entonces, la especial importancia que tiene proponer alternativas que contribuyan a mejorar los índices de rendimientos de estos sistemas de bombeo por la variación de las características del fluido y del proceso industrial.
Desde el punto de vista clásico todo problema de optimización matemática consiste en la búsqueda de los valores extremos (máximos y mínimos) absolutos o relativos de una función objetivo F que depende de los datos del problema y de ciertas variables entre las que se encuentran las llamadas variables de decisión (sus valores definen el universo de solución del problema) y otras llamadas variables intermedias que en ocasiones representan perturbaciones externas sobre las que el investigador no puede influir pero aportan datos, informaciones y conocimientos significativos. Los valores de todas las variables están sujetos a restricciones que generalmente se expresan mediante ecuaciones e inecuaciones donde intervienen las variables de decisión y las variables intermedias. Es esencial determinar para cuales valores de las variables de decisión la función objetivo alcanza sus extremos.
Desde un punto de vista más moderno y en función de resolver problemas tecnológicos (por ejemplo, los diseños), la optimización matemática de F sujeta a restricciones consiste en encontrar un conjunto de soluciones factibles (soluciones que cumplen con las restricciones) y entre estas soluciones factibles se selecciona una (o más de una) que maximice o minimice la función objetivo o que, al menos, estén por encima en el caso de buscar máximos, o por debajo si se buscan los mínimos, de cierta cota predefinida para la función objetivo. Esta cota en muchas ocasiones se define atendiendo a criterios de racionalidad. Entonces, cuando encontramos estas soluciones racionales, también estamos optimizando [8, 9]. El objetivo de la investigación estuvo relacionado con incrementar la eficiencia energética en el transporte de fluidos en la industria niquelífera mediante su modelaje y la resolución de un problema de optimización.
En el caso de las pulpas lateríticas varios factores tienen efecto directo en el comportamiento reológico y sus niveles son esenciales para mejorar la viscosidad de los mismos. Entre los factores involucrados en el proceso de transporte de hidromezclas del proceso de lixiviación ácida se pueden analizar los efectos de la concentración total de sólidos, la distribución de tamaños de las partículas, el pH, y la composición mineralógica y como factor principal la temperatura de la suspensión. Una vez preseleccionados los factores que pueden influir en el comportamiento de los parámetros reológicos se requiere de trabajo de laboratorio y procesamiento matemático de los valores experimentales obtenidos así como de un gran volumen de datos históricos del proceso de espesamiento y precalentamiento de pulpas que permiten la caracterización de las principales suspensiones minerales que se manipulan en esta etapa del proceso productivo.
Materiales y metodos
Las variables dependientes que son de especial interés para diseñar adecuadamente la operación eficiente del sistema de bombeo son:
μa: viscosidad aparente de la suspensión (denominado también Y1, Pa·s)
t0: Esfuerzo cortante inicial (denominado también Y2, Pa)
K: índice de consistencia (denominado también Y3, Pa·s n)
n: índice de flujo (denominado también Y4, adimensional)
Las variables independientes son los factores que definen las características reológicas de las hidromezclas lateríticas
s: parámetro característico de la granulometría (Coeficiente de Polidispersión), identificada como X1.
%S: contenido de sólidos (por ciento másico de sólidos en la pulpa), identificada como X2.
pH, identificada por X5.
Nrmin: Número mineral, identificada como X4.
Debido a la complejidad para controlar las variables X1 y X4 se diseñó heurísticamente un Experimento Factorial Completo 5x7 para las variables o factores X2 y X3.
En resumen el muestreo tiene 210 muestras físicas y se caracteriza por:
2 Muestras Compósitos para garantizar la representatividad de las otras dos variables independientes, 3 repeticiones para cada caso que argumentan la precisión de los resultados.
Descripción del muestreo
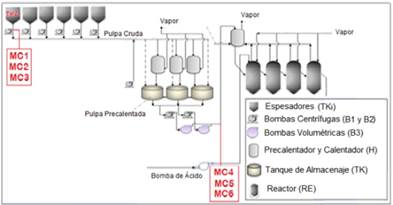
Se seleccionaron dos Unidades Demostrativas Productivas (UDP), ver Figura 1 y para el análisis experimental de la pulpa laterítica se tomaron dos puntos de muestreos:
Punto No. 1, pulpa laterítica a temperatura ambiente extraídas del fondo del espesador convencional (TK-1A) donde ocurre el proceso de sedimentación, donde debe lograrse un contenido de sólido en el cono del espesador entre (46 y 48) % por diseño.
Punto No. 2, pulpa laterítica con una temperatura de más de 90 oC, alcanzada esta temperatura en los precalentadores por contacto directo con vapor de 103,42 kPa a contracorriente. La muestra se toma en la descarga de las bombas B3 (bombas volumétricas).Vea figura 1.
Durante cuatro semanas alternas, según el frente minero de explotación y cada una hora de 7 am a 7 pm, se recogieron muestras en los puntos seleccionados de 500 ml de pulpa en un volumétrico de 1000 ml para preparar 12 compósitos en recipiente de 20 l. Se prepararon en total cinco muestras de 200 g con tres réplicas para las concentraciones de sólidos seleccionados de las Muestras Compósitos por UDP, contenidas en frascos tapados de 250 ml. Para la dilución de la pulpa inicial se añadió agua y para obtener concentraciones superiores al 40 % de sólidos se dejó sedimentar la pulpa y se le extrajo agua por decantación. A las muestras compósitos se le realizó el análisis químico, granulométrico y se le determinó el número de mineral, composición química y granulométrica.
Se decidió evaluar y tomar como referencias los históricos de cada variable:
Cinco intervalos de coeficiente de polidispersión: 0,1 a 3,0; 3,1 a 6,0; 6,1 de 9,0; 9,1 de 12,0; 15,1 de 19,0.
Cinco valores de porcientos de sólido: (37, 40, 43, 46 y 48) %.
Siete valores de temperaturas: (28, 40, 50, 60, 70, 80 y 90) °C.
Tres intervalos de Número de mineral: 0 de 6,9; 7 de 14; 14,1 de 20.
Equipos y Materiales
Los equipos utilizados para realizar los experimentos fueron los siguientes:
Para determinar características físicas de las muestras seleccionadas: espectrómetro de Fluorescencia de Rayos-X, analizador de tamaño de partículas del tipo “Analysette 22” COMPACT, balanza secadora Ohaus.
Para determinar propiedades reológicas: viscosímetro HAAKE VT 550, balanza técnica digital Mettler Toledo, balanza secadora Ohaus, agitador con impelente mecánico IKA RW 28, plancha térmica Cimarec, bomba de agua Master Flex Modelo 77601-10.
Además se utilizaron los utensilios: probetas de 500 ml, beakers de 500 ml, un recipiente de 20 l, jeringuillas de 20 ml, frascos de 250 y 1000 ml.
Procedimiento para la modelación y optimización operacional de sistemas de bombeo de pulpas crudas
La eficacia de un sistema de bombeo está dada por la garantía de ciertos valores (requeridos por el proceso tecnológico) de caudal y presión de las suspensiones en ciertos puntos del sistema de transporte. La eficiencia de estos sistemas está relacionada con el uso mínimo de los recursos humanos y materiales y del tiempo; en este caso reviste la mayor importancia el uso adecuado de la energía, adaptando la potencia de entrada del sistema a la carga mecánica exigida por las bombas en su transporte eficiente de hidromezclas de mineral laterítico. El diagnóstico operacional del sistema, una vez efectuado el diagnóstico a cavitación y sin detectar anomalías en cuanto a la ocurrencia de este fenómeno, se basa en la verificación de que el sistema se encuentra entregando el flujo requerido al proceso (Qreq) para el cual se brinda este servicio de transporte.
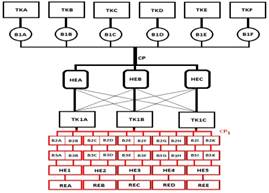
Esto es posible siempre y cuando el flujo de operación (QOp) sea mayor o igual al flujo requerido, o sea, QOp>Qreq. En caso contrario el sistema instalado no brinda los requerimientos industriales necesarios, por lo que se debe actuar para garantizar una operación eficiente mediante cambios en los parámetros de operación, la selección de una nueva bomba o el rediseño del sistema. El criterio económico debe decidir entre las variantes que se formulen. Parte de este diagnóstico operacional es la comparación entre el flujo de operación y el flujo para el punto de máxima eficiencia (Qd). Según [10], un equipo de bombeo se encuentra operando eficientemente cuando el flujo de operación posee una eficiencia que se diferencia en un 10 % de la eficiencia máxima de la bomba. Los flujos de operación que no se encuentren en esta zona de trabajo indican operaciones ineficientes producto de malas selecciones de los equipos de bombeo. El estudio se realizó en sistema de bombeo que va desde los espesadores hasta los tanques TK1A, TK1B y TK1C donde intervienen las bombas B1i (i=A,…, F), ver figura 2.
El bombeo de los flujos desde los depósitos de succión TKA,…, TKF hasta los depósitos de descargas TK1A, TK2B y TK2C, debe garantizar la productividad de la Planta de Lixiviación que son los requerimientos esenciales para estabilizar el flujo solicitado (FT) y la concentración de sólidos (PTo %).
También debe ser eficiente al considerar criterios energéticos.
Para cada tanque TKi (i=A, B, C, D, E y F) se conocen los siguientes datos:
Vai: Volumen actual, m3
Vui: Volumen actual útil, m3
CSi: Concentración de sólidos en el volumen actual útil, %
Ti: Temperatura, °C
Nrmini: Número de mineral, adimensional
si: Coeficiente de polidispersión, adimensional
Y se determinan los parámetros a partir del modelo reológicos obtenido:
μai: viscosidad aparente de la suspensión (denominado también Y1i, Pa·s)
t0i:Esfuerzo cortante inicial (denominado también Y2i, Pa)
Ki: índice de consistencia (denominado también Y3i, Pa·s n)
ni: índice de flujo (denominado también Y4i, adimensional)
Además se calculan las densidades ρi mediante la ecuación (1):
(1)
Para cada bomba centrífuga B1i se conocen los siguientes datos:
nrei: Velocidad estándar, r/min
nrmi: Velocidad máxima, r/min
Ecuación característica para la altura: vea ecuación (2).
(2)
Ecuación característica para la potencia: vea ecuación (3).
(3)
Nomograma de valores de la eficiencia R en función de los valores de Q y H.
Para cada tramo j de cada red hidráulica i se conoce:
Diámetro de la tubería: dtij (en m)
Longitud de la tubería: ltij (en m)
Coeficiente de resistencia de los accesorios [11]: ξij (adimensional)
Altura Hdescarga_i y Hsucción_i de la red hidráulica i: (en m)
Si se considera que todo este análisis se realiza para una hora de trabajo puede ser sustituido el volumen (dado en m3) por el flujo dado en m3/h. Entonces, se tiene que los flujos Q1, …, Q6 son numéricamente iguales a sus correspondientes volúmenes V1, …, V6.
Conociéndose la velocidad límite del depósito y la de sedimentación, se calculan las velocidades del fluido vfi[12, 13], para cada red hidráulica i mediante la ecuación (4):
(4)
El problema de optimización queda enunciado así:
¿Qué volúmenes de pulpa Vi (tal que 0≤Vi≤Vui) deberá aportar el correspondiente tanque TKi para garantizar en una hora de trabajo que cumplan las ecuaciones (5 y 6), de enlace CF1 y CF2 y se maximice una función objetivo relacionada con la eficiencia del proceso (CF3)
(5)
(6)
Condición de Máxima Eficiencia. Nótese que pueden ser una o varias expresiones cuantitativas o cualitativas
En la práctica la condición CF1 puede sustituirse por: ecuación (7).
(7)
Tal que la diferencia absoluta i=A F V i ≥FT sea tan pequeña como el proceso tecnológico lo permita.
Y la condición CF2 puede sustituirse por: ecuación (8).
(8)
Tal que la diferencia absoluta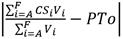 
sea tan pequeña como el proceso tecnológico lo permita.
Este problema cuyas variables de decisión Vi son continuas, es de complejidad significativa, por lo cual se propone la discretización de las variables de decisión para convertirlo en un problema de optimización combinatoria. Se propone el siguiente procedimiento:
Paso I. Discretizar con pasos h1i los correspondientes intervalos de búsqueda [0;Vi] en cada espesador. De esta manera queda planteado un Problema de Optimización Combinatoria sobre un espacio de búsqueda formado por todas las combinaciones posibles de los volúmenes tomados de cada Espesadores.
Paso II. Obtener el conjunto de soluciones factibles SF que son aquellas combinaciones C = (V1;V2;V3;V4;V5;V6) que cumplen las condiciones CF1 y CF2. Para ello se utiliza el método de búsqueda exhaustiva que prueba todas las combinaciones posibles y selecciona como factibles aquellas que cumplen dichas condiciones.
Paso III. Para cada combinación C del conjunto de SF hallar las velocidades nri, las potencias Ni y las eficiencias Ri para el transporte de pulpas.
Paso IV. Obtener para cada combinación C de SF el valor de cierta función objetivo y seleccionar cuáles combinaciones son las más convenientes para garantizar la eficiencia deseada.
Para concretar este paso IV pueden considerarse varias opciones para establecer la función objetivo. Las cinco propuestas que se presentan en esta investigación son las siguientes:
Minimizar 
Minimizar Dispersión de Flujos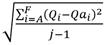 
donde j es el número de depósitos que se utilizan y Qai puede tomarse como:
Para todas las redes hidráulicas como la media aritmética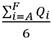 
Un valor deseado Qd que se asume para todas las redes hidráulicas según criterios tecnológicos del proceso real.
El valor particular para cada red hidráulica i que resulta de calcular: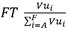 
Minimizar Dispersión de Velocidades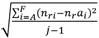 
donde nrai puede tomarse de maneras análogas a las explicadas en el inciso FO2.
Minimizar Dispersión de Potencias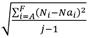 
donde Nai puede tomarse de maneras análogas a las explicadas en los incisos FO2 y FO3.
Maximizar el promedio de Eficiencia Mínima, o sea, tomar la combinación cuyo valor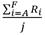 
sea máximo.
Nótese que con los argumentos correspondientes también pudieran establecerse otras funciones objetivo transformando y combinando las anteriores.
Paso V. Consiste en refinar las mejores soluciones obtenidas en el paso IV. Se aplica un procedimiento que consiste en:
Seleccionar los nuevos pasos h2i respectivamente menores que los pasos h1i definidos en el paso I y definir nuevas mallas en las vecindades de cada solución seleccionada en el paso anterior. Las vecindades deben tener dimensiones no menores que el correspondiente tamaño de h1i.
Para cada punto de cada nueva malla se comprueba si se cumplen o no las condiciones CF1 y CF2. De esta manera se obtiene un nuevo conjunto de soluciones factibles (SF).
Establecer una FO para este paso (la misma FO del paso IV u otra diferente), escogida entre las mencionadas anteriormente.
Se evalúa la FO seleccionada para este paso en cada punto de las nuevas mallas que son SF.
Las nuevas soluciones factibles se ordenan de acuerdo con los resultados de la nueva FO y se toma como solución óptima la mejor de esta lista.
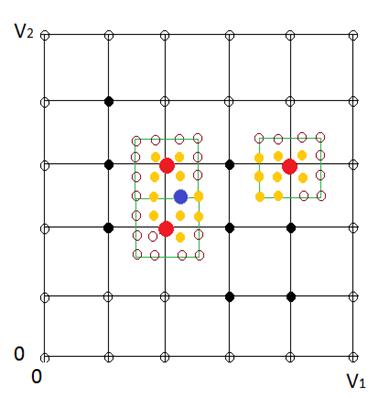
Después de ejecutarse los pasos IV y V (que en situaciones muy especiales pudiera repetirse para algunos puntos el paso V y obtenerse un segundo refinamiento) la solución óptima obtenida mediante la primera búsqueda discreta es una combinación de volúmenes Vi, tomados de cada espesador i, tal que cumple los requerimientos metalúrgicos CF1 y CF2 y además es energéticamente óptimo en el sentido de las FO escogidas. El procedimiento explicado se ilustra en la figura 3, donde se muestra el refinamiento para el caso de solo dos depósitos de succión con volúmenes V1 y V2. Se toman h11=V1/5 y h12=V2/5 de manera que es 36 el número de combinaciones de los valores del volumen de ambos depósitos.
Analizando el cumplimiento de las condiciones CF1 y CF2 para cada uno de los 36 puntos, se determina que 11 combinaciones las cumplen (puntos negros y rojos) y por tanto son soluciones factibles. Se seleccionó una FO entre las explicadas en IV y al evaluar las 11 SF en la FO, se encontraron los mejores valores en las marcadas con puntos rojos.
Ahora se toman nuevos valores h21=h11/3 y h22=h12/3 para formar nuevas mallas en las correspondientes vecindades de los mejores puntos (rojos). Cada nueva malla tiene 16 puntos (y algunos puntos pertenecen a más de una malla). Debe verificarse para cada uno de estos puntos si es solución factible (SF), obteniéndose con respuesta positiva las del color amarillo. Luego, después de seleccionar la FO para el refinamiento, evaluarla para cada solución factible de las mallas del refinamiento. La de mejor resultado en estas evaluaciones identifica la combinación volumétrica (con adecuado porcentaje de sólidos) más eficiente (en este caso en azul).
Debe señalarse que para seleccionar los mejores puntos de la segunda partición puede considerarse la misma función objetivo que se utilizó en la primera partición o pueden considerarse funciones objetivos diferentes e incluso combinaciones. Son los requerimientos tecnológicos de productividad, concentración de sólidos y los relacionados con la eficiencia energética, los factores que definen la selección de cada función objetivo. Por ejemplo podrían establecerse en conjunto las funciones objetivo:
Primera partición: FO2 + Segunda partición: FO1
Primera partición: FO2 + Segunda partición: FO5
Primera partición: FO5 + Segunda partición: FO2
En el proceso de bombeo de pulpa cruda puede notarse que en la tubería concentradora CP se produce un proceso de mezclado que homogeniza las propiedades de la pulpa. En el proceso de precalentamiento (HEA, HEB y HEC) varían en cada uno de ellos la temperatura y la concentración de sólidos de las pulpas y estos tres flujos de pulpa precalentada se envían a los tanques TK1A, TK1B y TK1C lo cual inicia cierta mezcla y homogenización que se completa en la red única CP1 desde donde succionan las 10 bombas B2i (i=A,B,…, K). Entonces puede asumirse que tienen valores únicos las propiedades concentración de sólidos, temperatura y número de mineral en CP1.
Composición química de las muestras utilizadas
La materia prima mineral que ingresan al proceso LAP poseen contenidos de Fe en el orden de 35,5 % a 53,4 %, incluyendo otros componentes como el Al (de 2,23 % a 5,99 %) y el Mg (de 0,1 % a 3,3 %), esto confirma la naturaleza ferruginosa de las muestras de laterita. En la tabla 1, se recoge las composición de las cuatros muestras seleccionadas.
Tabla 1 Composición química y número de mineral de las muestras estudiadas
| Elemento, % | Concentración de cada elemento en las muestras | |||
|---|---|---|---|---|
| MC1 | MC3 | MC5 | MC6 | |
| Ni | 1,21 | 1,28 | 1,22 | 1,23 |
| Co | 0,79 | 0,3 | 0,115 | 0,20 |
| Fe | 42,9 | 43,9 | 43,2 | 43,3 |
| Mg | 1,69 | 1,94 | 1,72 | 2,6 |
| Al | 4,41 | 4,32 | 4,42 | 4,44 |
| SiO2 | 2,25 | 7,12 | 6,39 | 6,52 |
| Cr | 1,51 | 1,63 | 1,56 | 1,57 |
| Mn | 0,38 | 0,75 | 0,74 | 0,73 |
| Cu | 0,027 | 0,04 | 0,028 | 0,028 |
| Zn | 0,034 | 0,036 | 0,036 | 0,036 |
| Ni + Co | 2,00 | 1,53 | 1,335 | 1,53 |
| Nrmin | 3,97 | 9,65 | 9,48 | 12,19 |
Distribuciones granulométricas
Existen varios modelos para describir la distribución granulométrica de partículas sólidas en procesos de reducción y de clasificación de tamaño. Entre ellos se encuentran los modelos de Gaudin-Schuhmann, de Rosin-Rammler-Sperling, de Gaudin-Meloy, en investigaciones recientes [14], se ha determinado que el método más efectivo para el análisis granulométrico es el de Rosin-Rammler-Sperling, pero se ha comprobado que ninguno es capaz de describir la granulometría de las materias primas del proceso de lixiviación ácida, por lo que se escoge el modelo matemático utilizado por [15] , de describir según esta autora la distribución granulométrica de estas suspensiones. Vea ecuación (9).
(9)
Donde: DN= Dp / D50 y YN = YB / Y50; DN: Diámetro normalizado; YN: Su correspondiente fracción normalizada; D50: Es la mediana de la distribución acumulativa; Y50 = 0,5 (50 %) es la fracción de sólidos correspondiente a la mediana de la distribución; BN: Coeficiente adimensional.
Las distribuciones granulométricas de la MC1 se presentan y puede apreciarse que todas están constituidas por partículas pequeñas, inferiores a 50 µm, que son las que le confiere propiedades plásticas a las pulpas. Existe un predominio de las fracciones finas de forma general y el D80 se corresponde con el de partículas menores a 7 µm, lo cual indica que el 80 % de la muestra presenta un diámetro inferior a este valor, por tanto, las partículas más finas son mayoritarias y determinan la velocidad de sedimentación de este mineral, así como su comportamiento reológico, es decir, las partículas de todos estos materiales tienen un comportamiento propio de sistemas polidispersos, como se muestra en la figura 4.
Resultados del análisis reológico de la pulpa laterítica a temperatura ambiente
Para obtener los valores de esfuerzo de corte se determinó una media aritmética de las tres réplicas por cada gradiente de velocidad con su desviación estándar y coeficiente de variación el cual no excedió del 5 %.
A partir de los gráficos de los valores de esfuerzo cortante y gradiente de velocidad todas las muestras describen el modelo de Bulkley-Herschell pseudoplástico, se obtienen los parámetros reológicos (esfuerzo cortante inicial, índice de consistencia e índice de flujo) con ayuda de la aplicación informática para la modelación de las curvas de flujo [5, 15].
Los resultados obtenidos en el análisis de la muestra del espesador TKA, ver tabla 2. Se evidencia la tendencia de los parámetros reológicos al aumentar las concentraciones de sólidos a temperatura ambiente, se incrementa la viscosidad aparente, el esfuerzo de corte inicial y el índice de consistencia y disminuye el índice de flujo, este comportamiento es el esperado, que demuestra las propiedades plásticas de las hidromezclas lateríticas [16, 17, 18, 19].
Tabla 2 Influencia de la concentración de sólidos en los parámetros reológicos TKA
| Concentración de sólidos, % | Viscosidad aparente, Pa·s | Modelo ajustado | R |
|---|---|---|---|
| 37 | 0,402 |
|
0,9997 |
| 40 | 0,660 |
|
0,9998 |
| 43 | 0,907 |
|
0,9999 |
| 46 | 1,299 |
|
0,9999 |
| 48 | 1,965 |
|
0,9999 |
Operación y optimización de sistemas de bombeo de hidromezclas lateríticas
Para garantizar la productividad diaria de Planta Lixiviación se necesitan entre 9 000 y 10 000 t/día de mineral, lo que equivale a 375-417 t/h. Para lograrlo se deben extraer entre 1600 y 1800 t/día de cada espesador, las bombas centrífugas deben tener un caudal de extracción de 450 a 478 m3/h y la concentración de sólidos deseada en el cono del espesador, como consecuencia de la velocidad de sedimentación que corresponda para los yacimientos en explotación. A continuación se caracteriza una situación típica de la operación con 5 espesadores en funcionamiento. Se conoce el volumen actual, el volumen útil de extracción, el % de sólidos, la temperatura ambiente, los parámetros reológicos y la densidad, ver tabla 3.
Tabla 3 Características físicas y reológicas de las pulpas contenidas de cada depósito TKi (i=A,…,K)
| Sedimentador | TKA | TKB | TKC | TKD | TKE | TKF |
|---|---|---|---|---|---|---|
| Volumen actual, m3 | 65000 | 55000 | 45000 | 25000 | 800 | 65000 |
| Volumen útil, m3 | 950 | 950 | 950 | 0 | 800 | 950 |
| Concentración de sólidos, % | 46 | 45 | 47 | 40 | 44 | 47 |
| Temperatura, °C | 28 | 28 | 28 | 28 | 28 | 28 |
| Viscosidad aparente, Pa·s | 1,44 | 1,22 | 1,68 | 0,62 | 1,03 | 1,69 |
| Esfuerzo cortante inicial, Pa | 29,86 | 27,22 | 35,49 | 10,92 | 36,04 | 41,65 |
| Índice de consistencia, Pa·sn | 9,49 | 8,57 | 10,97 | 5,23 | 8,77 | 11,33 |
| Índice de flujo | 0,65 | 0,64 | 0,66 | 0,62 | 0,60 | 0,65 |
| Densidad, g/cm3 | 1493,4 | 1477,6 | 1509,6 | 1403,1 | 1462,1 | 1509,6 |
Además, se tienen las características hidráulicas de cada tubería. Por ejemplo, en la tabla 4, se muestran las características de la tubería del depósito TKA.
Tabla 4 Características de la tubería del depósito TKA
| Tramo | Altura, m | Resistencia | Longitud, m |
|---|---|---|---|
| 1 | 5,95 | 6,85 | 112 |
| 2 | 6,65 | 9,6 | 314 |
Si se consideran las características del fluido a transportar y las características de la red hidráulica desde el fondo del TKA hasta los tanques de almacenaje, el coeficiente de corrección de carga es CH= 0,505 obtenido por el modelo matemático de la pulpa laterítica que relaciona la concentración de sólidos, la temperatura y el número de mineral [20], el que permite obtener los modelos de carga y potencia para las condiciones de operación. Para lograr la productividad de la bomba centrífuga del espesador TKA, tienen que vencer una altura de bombeo de 17,20 m y una presión de descarga 353,86 kPa, una potencia de bombeo de 80,60 kW, con una velocidad de 1158 r/min y una eficiencia del 72 %.
Este análisis se realiza para cada bomba centrífuga instalada en el fondo de cada espesador con un algoritmo de optimización para la toma de decisión de los parámetros de operación que permitan garantizar la productividad de la planta en volúmenes de mineral y con altas concentraciones de sólidos. En la figura 5, se muestra la ventana de la aplicación informática programada para esta ocasión que facilita la toma de decisión de las operaciones según los requerimientos productivos de las Plantas de Espesadores y Lixiviación.
Evaluación del algoritmo de optimización propuesto para pulpa cruda
Para aplicar el algoritmo de optimización se asumen las condiciones siguientes:
Se garantiza la productividad cada una hora con un volumen de (1600±5) m3 y un promedio de (46±1) % de sólidos.
Si el volumen útil de TKD es 0, entonces de este depósito no se bombea.
El número seleccionado de posibles valores por depósito se tomó igual a 61, de manera que el número de combinaciones a analizar es 19 770 609 664. De estas combinaciones, en la búsqueda general, 2 800 850 cumplieron las condiciones de factibilidad respecto al volumen solicitado, a la concentración de sólidos y la velocidad máxima permisible.
Las combinaciones factibles se ordenaron de mayor a menor promedio de eficiencia y para el refinamiento se consideraron las 100 combinaciones de mejor eficiencia promedio.
Para cada búsqueda refinada se tomaron redes de 7 puntos en cada depósito, de manera que se analizaron en cada refinamiento un total de 16 807 combinaciones de las cuales se aceptaron solo las que son factibles. El total de combinaciones factibles es 2 927 250.
Se asumen las características físicas y reológicas mostradas en la tabla 3.
La función objetivo (FO) a optimizar puede tomarse de diversas formas. Si asumimos que FO es la condición para que se minimice la suma de las potencias demandadas, se obtienen los resultados de la tabla 5.
Tabla 5 Resultados obtenidos con FO. Menor Suma de Potencia
| Variables | i=A | i=B | i=C | i=D | i=E | i=F |
|---|---|---|---|---|---|---|
| Qi, m3/h | 414,66 | 456,48 | 451,63 | 0 | 273,07 | 0 |
| Hi, m | 36,44 | 31,37 | 34,60 | 0 | 49,61 | 0 |
| ni, r/min | 1072 | 904 | 1017 | 0 | 1287 | 0 |
| Ni, kW | 83,86 | 76,80 | 85,83 | 0 | 87,06 | 0 |
| R i, % | 0,73 | 0,75 | 0,74 | 0 | 0,61 | 0 |
| Nmotor, kW | 92,24 | 84,48 | 94,41 | 0 | 95,76 | 0 |
Se evidencia en la tabla 5, que en la menor suma de potencias la extracción para el Espesador F, no se realiza y para el Espesador E es de 273,07 m3/h, para estos dos Espesadores la distancia es superior a los 800 m, por lo es preciso vencer mayor altura; en el caso del TKE es de 49,61 m.
Por otra parte, si se considera la FO como el Mayor Promedio de Eficiencia, se obtienen los resultados de la tabla 6.
Tabla 6 Resultados obtenidos con FO. Mayor Promedio de Eficiencia
| Variables | i=A | i=B | i=C | i=D | i=E | i=F |
|---|---|---|---|---|---|---|
| Qi, m3/h | 362,21 | 362,21 | 454,06 | 0,00 | 426,30 | 0,00 |
| Hi, m | 35,84 | 32,98 | 34,62 | 0,00 | 50,44 | 0,00 |
| ni, r/min | 1026 | 925 | 1019 | 0,00 | 1417 | 0,00 |
| Ni, kW | 73,39 | 66,44 | 86,14 | 0,00 | 118,96 | 0,00 |
| R i, % | 0,72 | 0,72 | 0,75 | 0,00 | 0,72 | 0,00 |
| Nmotor, kW | 80,72 | 73,08 | 94,75 | 0 | 130,85 | 0 |
Las concentraciones de sólidos que están en el TKA con 46 % y TKC con 47 % serían las mayores que se pueden alcanzar, con estas condiciones las bombas con velocidades por encima de 1000 r/min logran el caudal de extracción deseado.
Discusión y resultados
Una gran parte de los gastos capitales durante el hidrotransporte lo constituyen los gastos de energía eléctrica, su economía es una de las direcciones estratégicas de la producción en la actual etapa. Una correcta selección y organización en la explotación del equipamiento de bombeo en régimen económico permite el ahorro de la energía eléctrica y aumentar la efectividad del transporte hidráulico y los problemas que esta puede causarle al medio circundante. A partir de los modelos matemáticos de los parámetros energéticos pueden determinarse la productividad del sistema de bombeo de hidromezclas lateríticas cruda y precalentada como flujos, cargas, pérdidas hidráulicas, potencia y eficiencia en función de los parámetros reológicos de los fluidos que transportan. Mediante un diagnóstico de la operación en las instalaciones analizadas se fundamentó la aseveración de que en la actualidad la capacidad de bombeo está reducida al no tomarse en cuenta los puntos de máxima eficiencia de las bombas instaladas.
A partir de simulaciones y pronósticos facilitados por la aplicación informática auxiliar desarrollada se fundamentó que los resultados obtenidos tienen utilidad práctica para la toma de decisiones tecnológicas que generen impacto económico y ambiental positivo. Se obtienen modelos matemáticos de los parámetros reológicos de viscosidad aparente, esfuerzo cortante inicial, índice de consistencia e índice de flujo de las hidromezclas lateríticas cruda y precalentada, en función de los factores temperatura, contenido de sólidos y composición química y granulométrica que permiten resolver las ecuaciones que describen el comportamiento de las curvas características carga - descarga de las redes y de las bombas.Se obtienen modelos matemáticos de parámetros energéticos que determinan la productividad del sistema de bombeo de hidromezclas lateríticas cruda.
Conclusiones
A partir de una apropiada discretización del modelo del sistema de bombeo de pulpa cruda y de la aplicación del procedimiento de optimización combinatoria se obtuvieron los parámetros de explotación de este sistema como flujos, cargas, pérdidas hidráulicas, potencia y eficiencia en función de los parámetros reológicos de los fluidos que transportan. Se demostró con el diagnóstico de operación que en las instalaciones analizadas se reduce la capacidad de bombeo al no tomar en cuenta los puntos de máxima eficiencia de las bombas instaladas. Se demostró la utilidad práctica de los resultados para la toma de decisiones tecnológicas con un impacto económico positivo a partir de simulaciones y pronósticos que facilitan la aplicación informática.
