Artículo Original

Evaluación del comportamiento de un algoritmo para la secuenciación en un taller de flujo con tiempos dependientes de la secuencia

Evaluation of the behaviour of a sequences elaboration algorithm in a flow shop with depending on the sequence times

Alberto Fiol-Zulueta^I, José Arzola-Ruíz^I, Adriano da Silva-Carvalho^II
I. Departamento de Matemática. Facultad de Ingeniería Mecánica
Instituto Superior Politécnico "José Antonio Echeverría" - CUJAE
Calle 114 #11901 e/119 y 127. Marianao. La Habana. CP 19390. Cuba
E-mail: [e-mail], [e-mail]
II. Facultad de Ingeniería, Universidad de Oporto. Portugal
E-mail: [e-mail]

---

Resumen

En el trabajo se realiza la evaluación del comportamiento de un algoritmo propuesto para la secuenciación en un taller de flujo con tiempos dependientes de la secuencia, utilizando un método híbrido basado en el Algoritmo de Búsqueda del Extremo de una Función de un Código Variable y la metaheurística de Búsqueda Dispersa. Asimismo, se analizan casos obtenidos de la aplicación en un taller mecánico de una industria nacional.

Palabras claves: secuencias, taller de flujo, metaheurística.

---

Abstract

In this paper the evaluation of the behaviour of a proposed algorithm is made for the sequence of events in a stream flow in a workshop with dependent moments of the sequence using a hybrid method based on the SEARCH OF THE EXTREME OF A FUNTION OF A VARIABLE CODE ALGORITHM AND THE DISPERSED SEARCH METHOD ALGORITHM In the same way, cases obtained from the application in a workshop of the national mechanical industry are analysed.

Key words: scheduling, flow shop, metahuristic.

---

 

 

INTRODUCCIÓN

Scheduling o secuenciación es el proceso de seleccionar entre planes alternativos y asignar recursos y tiempos al conjunto de actividades del plan o schedule. En resumen, secuenciación es un proceso de optimización donde recursos limitados son asignados en el tiempo.

Con la temática de planificación y secuenciación se tienen un conjunto de modelos y técnicas de Investigación Operativa, los que permiten solucionar varios de los problemas que surgen en diferentes actividades de la vida real. En estas aparecen situaciones en las que se necesita de forma óptima solucionar la asignación de recursos a distintas actividades durante determinado instante de tiempo.

Los modelos iniciales relacionados con esta temática surgen en los años 50 del siglo pasado apareciendo en la literatura especializada muchos algoritmos que resuelven el problema de la planificación de n actividades sujetas a restricciones de precedencias, restricciones de retrasos (o sea, retrasos mínimos y máximos permitidos entre actividades) y restricciones de tiempo (o sea, tiempos de inicio más tempranos y tiempos de finalización más tardíos permitidos para cada actividad).

En esta dirección se presentan variados problemas reales que se pueden catalogar y estudiar en función de diferentes parámetros que permiten analizar las distintas posibilidades que se pueden presentar en la práctica. Una buena parte de las investigaciones que se realizan en esta dirección se centran en los problemas de planificación determínistica, para los que, a pesar de que han sido desarrollados muchos modelos y técnicas de solución, continúan surgiendo nuevas líneas con el objetivo de mejorar las técnicas existentes.

Además, se demuestra que muchos problemas de planificación existentes son "NP-completo".
Un problema de este tipo es tal que se presume que no existe un algoritmo capaz de solucionar el problema en una cantidad de tiempo acotada por una función polinómica del tamaño de los datos.

Para solucionar un problema "NP-completo" de un tamaño no trivial, es posible la utilización de alguno de los siguientes enfoques:

• Aproximación: un algoritmo que rápidamente encuentra una solución aproximada que está dentro de un cierto (y conocido) rango alrededor de la solución óptima. En realidad no se puede asegurar la existencia de buenos algoritmos de aproximación para todos los problemas "NP- completo" y en muchos casos es suficiente el hecho de encontrar una buena aproximación para solucionar el problema
• Solución probabilística: un algoritmo que pueda presentar un comportamiento promedio bueno para una distribución dada de instancias del problema.
• Casos especiales: un algoritmo que probablemente sea rápido si las instancias del problema pertenecen a cierto caso especial.
• Heurístico: un algoritmo que trabaja "razonablemente bien" en muchos casos, pero para el cual no existe prueba de que siempre sea rápido

En los últimos años se desarrolló y se publicó por Arzola [1] , el así llamado Enfoque Integrador para el Análisis y la Síntesis de Sistemas de Ingeniería para la Preparación y Toma de Decisiones bajo Criterios Múltiples. La solución de estas tareas tiene mucho que ver, por un lado, con el problema de la descomposición de tareas de gran complejidad y de la composición de soluciones entre las tareas resultantes de esta descomposición y, por el otro, con la conciliación de criterios interrelacionados. Esta conciliación se realiza mediante alguna estructura la que necesariamente tiene que ver con la estructura del modelo matemático del objeto o proceso asociado.

A partir de este enfoque se utiliza un método híbrido basado en el Algoritmo de Búsqueda del Extremo de una Función de un Código Variable [2] y la metaheurística de Búsqueda Dispersa [3, 4] para la solución de una tarea de secuenciación en un taller de flujo híbrido con tiempos dependientes de la secuencia analizado en un trabajo anterior presentado por los autores.

1. Características de la implementación computacional

La experiencia computacional se basa en la ejecución de tres procedimientos diferentes:

1. Aplicación del algoritmo de búsqueda de la solución inicial.
2. Aplicación de un algoritmo para obtener subpoblación, a partir de la utilización del algoritmo principal a un por ciento de toda la población y posteriormente la selección de una muestra de los elementos favorables obtenidos anteriormente.
3. Aplicación de un procedimiento de refinamiento de las soluciones.

La acción de repetir consecutivamente los métodos expuestos sobre el mismo conjunto de datos no reporta ninguna utilidad para el análisis, pues no se aprecian grandes variaciones desde una experiencia a la siguiente. El procedimiento de búsqueda de elementos que pertenezcan a las vecindades de los individuos que pertenecen a la población óptima y que tengan un valor menor de la función objetivo, para sustituir a cada uno de los elementos anteriores presenta una gran aleatoriedad, pero debe ser aplicado cuidadosamente, pues puede conducir a una degeneración de la población.

Dentro de la gama de soluciones que es posible calcular por la implementación computacional del algoritmo, ésta es la que mejores resultados proporciona al decisor, aunque se debe señalar que no se debe interpretar como soluciones óptimas globales, sino como aproximaciones más o menos cercanas a éstas. Precisamente la calidad de una heurística puede ser estimada por la proximidad media de las soluciones encontradas al óptimo global. Este hecho hace que no sea precisa la repetición de experiencias.

Para la implementación del algoritmo se trabaja sobre un conjunto de datos agrupados de la siguiente forma:

• Caso 5 trabajos y 3 máquinas
• Caso 8 trabajos y 6 máquinas
• Caso 10 trabajos y 9 máquinas

Cada juego de datos consta de una parte fija (los tiempos de preparación, los de proceso unitarios y la velocidad de cada máquina para fabricar cada artículo) y una parte variable (la asociada a los datos de los pedidos).

A fin de agilizar y automatizar los cálculos asociados al método de solución propuesto, se desarrolla una aplicación informática, el algoritmo de solución expuesto fue programado en lenguaje C++ en una Pentium IV de 512 Mb de RAM y disco duro con capacidad de 80 Gb.

Para la obtención de los resultados, los pasos a seguir son los siguientes:

1. En primer lugar, es necesario realizar la entrada de datos que se desea evaluar.

2. A continuación, utilizando en la Salida de Datos, el comando "Generar Población" permite obtener las mejores soluciones organizadas en función del valor de la función objetivo.

3. El comando "Simulación" muestra las opciones posibles a partir de la secuencia seleccionada y presenta el tiempo de ejecución del CPU y una tabla de resultados.

La implementación computacional del algoritmo que se diseña para secuenciar un conjunto de N trabajos en un sistema taller de flujo híbrido con K etapas, permite que se le trate como un sistema cerrado en el que entra una secuencia y se obtiene la asignación y secuenciación de los trabajos en las máquinas de cada etapa.

Las heurísticas que se utilizan se dividen en dos partes: un procedimiento para obtener una secuencia inicial y un procedimiento de optimización local sobre la secuencia inicial.

Los datos de entrada se conservan y actualizan en una base de datos diseñada al efecto. La información correspondiente a las variables de coordinación se introduce con ayuda de la interfase de entrada para cada corrida del software. En cada ejecución del software se genera una población de secuencias de producción correspondientes a los trabajos a programar. No se limita el umbral de planificación, pues este depende del esquema de planificación volumétrica establecido en la entidad dada: puede tratarse de un plan para la semana, el mes, el trimestre, etc. En todos los casos se trata de secuenciar de la mejor forma todo el paquete de órdenes de producción que deben ser satisfechas.

Los datos de entrada cuyos valores se introducen en cada ejecución del software son:

Las variables de coordinación cuyos valores se introducen en cada ejecución del software son:

• El número de trabajos que precisan ser secuenciados en la etapa inicial.
• El valor deseado de las tiempos de terminación y de la cantidad de trabajos atrasados, el que generalmente se adopta igual a 0
• Las fechas de realización sin tardanza de los trabajos
• Matriz de las fechas de realización de los trabajos
• Matriz de tiempos de proceso unitarios de cada artículo en cada máquina o etapa
• Matriz correspondiente a las velocidades relativas de las máquinas por etapas
• Matriz de tiempos de preparación para cada máquina al pasar de fabricar un artículo a otro diferente. Cada máquina j requiere unos tiempos de trabajo o procesado para elaborar cada uno de las piezas i, Tmp:
• Los tiempos de preparación, Tps, debido a la secuencia, los cuales se dan para cada una de las etapas en forma de tablas.
• Las fechas de finalización se calculan automáticamente
• El valor del peso l que es una decisión que puede tomar el decisor, de acuerdo a la importancia que le otorgue a los indicadores de eficiencia.

Una vez entrados los datos se procede a la subdivisión del número total de posibles secuencias, para obtener, una población de secuencias racionales para la etapa inicial, ordenadas de acuerdo al valor de la función objetivo. El decisor tiene la posibilidad de seleccionar una de ellas.

En el algoritmo, se utiliza que:

1. El tiempo de preparación, es el que incluye el tiempo de preparación debido a la secuencia y el tiempo de preparación debido a la máquina.

2. La fecha de finalización dj se calcula mediante la fórmula dada en [5] :
dj =[ Total de los tiempos medios de preparación del trabajo en todas las etapas] [Tiempo medio de

procesamiento del trabajo en una máquina] x U(0,1) donde:

• Tiempo medio de procesamiento del trabajo en una máquina es igual a la suma del tiempo medio de preparación y el tiempo de procesamiento unitario de todos los trabajos en todas las máquinas entre el número de máquinas.
• El primer sumando es la suma de todos los tiempos de preparación debido a la secuencia entre las cantidades de trabajos.
• El segundo sumando es la suma de los tiempos de procesamiento unitario de cada trabajo en todas las etapas.
• En el tercer sumando, el primer paréntesis es la cantidad de trabajos menos uno, el segundo paréntesis está explicado arriba, no obstante se suman todos los tiempos de preparación en cada una de las etapas y se divide por el número de etapas con la suma de todos los tiempos de preparación unitario y se divide entre el número de etapas y el último paréntesis toma valor 1 indicando que el trabajo está atrasado, de no estarlo se le da el valor 0.

3. El tiempo de operación se calcula o sea es igual al tiempo de procesamiento más el tiempo de preparación.
4. La fórmula para calcular donde los valores que intervienen en la división se sacan de la base de datos.

y así sucesivamente con cada trabajo, con el objetivo de en esta etapa organizarlos utilizando:

1. La regla llamada SPT: ordenar de forma creciente los tiempos de procesamiento.
2. La regla llamada MST: mínimo tiempo de holgura, donde la holgura se calcula mediante , o sea fecha de entrega menos el tiempo de operación.

Después de la selección que se realiza, una vez que comienza el primer trabajo de la secuencia seleccionada, es posible que se incorporen nuevos trabajos, incluidos los de clientes de alta prioridad, que no se corresponda con la secuencia previamente elaborada con la ejecución real del plan, como consecuencia de diferentes imprevistos o por la incertidumbre misma de los parámetros del modelo. Para estos y otros casos el algoritmo de manera dinámica realiza una nueva secuenciación, ajustada a las nuevas realidades de estos nuevos trabajos.

Por otra parte, comienza la preparación de la conciliación con la próxima etapa, a partir de considerar el tiempo de preparación entre las máquinas, para poder generar una secuencia para esta etapa. Este procedimiento se realiza en cada una de las etapas hasta obtener la secuencia para cada una de las etapas y de cada trabajo en su tránsito por el taller de flujo.

En cada nueva etapa, se tiene un inventario de trabajos a realizar en esta, al que se adiciona la salida de trabajos de la etapa precedente. La secuencia a realizar en esta nueva etapa se corresponde con sus condiciones internas y con las condiciones externas establecidas para la producción terminada.

Salida de resultados

• Los resultados de salida proporcionados por el software están constituidos por un listado de secuencias organizadas que dan lugar a los menores retrasos, para que pueda ser seleccionada una de ellas por el usuario.
• Permite también simular con los datos del problema el comportamiento de la secuenciación para las secuencias generadas y obtener la correspondiente matriz de los tiempos de procesamiento total y por etapa de cada trabajo.
• Se entrega la matriz de tiempos de procesamiento total y por etapa de cada trabajo
• Permite obtener el tiempo de máquina que demora la generación de las secuencias.

2. Comparación del procedimiento desarrollado con resultados de la bibliografía

En calidad de método de referencia para la comparación se utilizan los Algoritmos Genéticos reportados en las Memorias del proyecto Programación de pedidos en un taller con máquinas en paralelo y tiempo de preparación [6], por constituir uno de los más eficientes entre los que aparecen en la bibliografía especializada.

Se conoce que para el buen funcionamiento o desarrollo de una metaheurística es muy importante la apropiada calibración de los parámetros, lo cual constituye una parte integral en el desarrollo de cualquier procedimiento metaheurístico. Este proceso de calibración tiene como objetivo determinar un rango de valores de los parámetros, de tal modo que el desarrollo de la metaheurística trabaje bien sobre un amplio rango de tipos de problemas.

Para lograr esto, se busca un conjunto de parámetros que sean robustos para un pequeño conjunto de problemas representativos y después se emplean en los diferentes conjuntos o instancias de problemas. Para la calibración de los parámetros, en este trabajo se selecciona un pequeño número de instancias con diferentes atributos que abarca un rango de diferentes tipos de problemas, y con posterioridad se fijan los valores de estos parámetros.

El próximo paso para la selección de los problemas es identificar los valores de los parámetros que se requieren. En la Tabla 1 se puede observar el procedimiento de generación de los valores, con parámetros semejantes a los propuestos en 6 , el que se utiliza como patrón de comparación

Tabla 1. Características de los parámetros para los problemas seleccionados

En el desarrollo del experimento para cada uno de los casos que se analizan se generan 30 problemas diferentes y se obtiene el promedio de estas para cada una de las combinaciones.

Se comparan los resultados ofrecidos por el algoritmo de referencia frente a los obtenidos por el algoritmo desarrollado en este trabajo. A partir de esta comparación se discierne cuál de los dos ofrece los mejores resultados al tipo de problema tratado. De ahí que los datos empleados en la implementación del programa son idénticos en ambos trabajos.

Tratamiento de los resultados

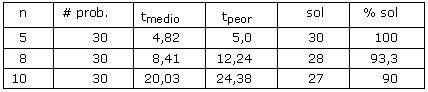
En la Tabla 2 se presenta el tiempo medio promedio de CPU, el peor de los tiempos de los problemas analizados y la cantidad de problemas solucionados mediante el algoritmo que se propone en este trabajo.

Tabla 2. Valores de los tiempos de CPU

donde:

# prob.: número de problemas generados

t_medio: promedio de los tiempos de ejecución

t_peor: máximo de los tiempos de ejecución entre los problemas que no exceden el tiempo límite

sol: número de problemas resueltos antes del límite de tiempo

% sol: % de problemas resueltos antes del límite de tiempo

Figura 1. Comparación de los tiempos de CPU

Como se puede observar en la Figura 1, el aumento de la cantidad de trabajos trae como consecuencia un mayor consumo de tiempo de CPU, pues la cantidad de evaluaciones aumenta en dependencia de dicho número.

A continuación se presentan las comparaciones que se realizan entre los dos algoritmos para cada uno de los casos que se analizan:

Tabla 3. Resultados de las comparaciones realizadas

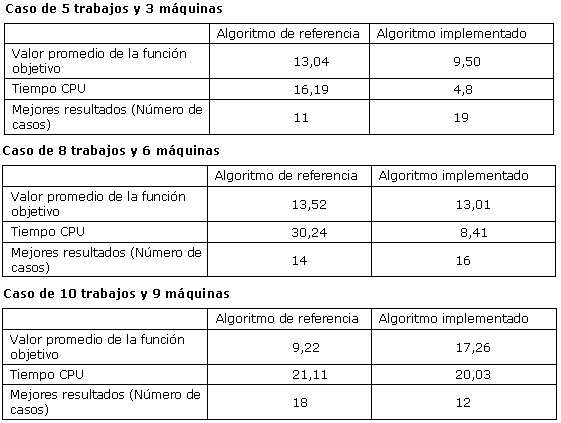
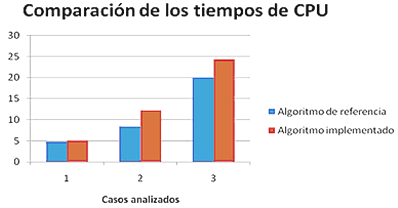
Figura 2 Comparación entre los valores promedios de la función objetivo

Conclusiones de la comparación

Se compara el algoritmo implementado con el de referencia para la evaluación de los resultados que se obtienen de una aplicación en igualdad de condiciones. Es decir, en ambos casos se aplican las heurísticas bases como único procedimiento de solución, sin emplear previamente otras heurísticas que proporcionen un punto de partida mejorado para el algoritmo.

En estas circunstancias, a tenor de los resultados, se pueden extraer ciertas conclusiones:

• El algoritmo que se implementa aporta, en líneas generales, mejores resultados que el algoritmo de referencia en lo que respecta al valor promedio de la función objetivo para los problemas más simples (dentro de la complejidad que presentan), como es el caso de determinar la secuencia de programación para el caso de 5 trabajos en 3 máquinas disponibles.
• Para problemas de complejidad intermedia, ambos algoritmos son apropiados, con una cierta ventaja para el algoritmo que se implementa.
• Para problemas con mayor complejidad, resulta más apropiado el algoritmo de referencia, pues en general, con él se obtienen un menor valor promedio de la función objetivo.
• Dentro de las experiencias de la implementación, se comprueba que a medida que se incrementa el tamaño del problema, toma un mayor tiempo computacional, la exposición de la solución.
• El tiempo de proceso de la CPU del algoritmo que se implementa es menor que el requerido por el algoritmo de comparación, siendo similar en todos los niveles de complejidad de los datos de entrada. Esto hace que, ante dos soluciones similares aportadas por ambos algoritmos, el tiempo de cálculo sea el factor que determine la elección de uno sobre el otro.

Por lo que respecta al valor promedio de la función objetivo, en líneas generales, si se comparan en las mismas condiciones, ambos métodos son adecuados para la obtención de una secuencia de programación de operaciones aceptable.

También cabe decir que la diferencia entre ellos no es significativa, pero aun así se aconsejaría utilizar la heurística que se implementa para solucionar el problema de secuenciación en un sistema de flujo de taller híbrido con tiempos de preparación dependientes de la secuencia.

3. Aplicación del algoritmo en procesos de producción en una industria cubana

Los casos expuestos se han localizado en el ámbito de una empresa real del sector de la industria metalmecánica, aunque es de aplicación a cualquier empresa en la que coexistan dos o más etapas de fabricación y exista la necesidad de procesar artículos en diferente orden en cada una de ellas para la disminución o eliminación de ineficiencias.

Se parte de los valores dados por las normas de tiempo establecidas en dicha empresa y se realiza la debida adecuación a la forma de entrada de datos que requiere la implementación computacional; se realizan las corridas y se presenta un conjunto de posibles secuencias, de las cuales el decidor puede seleccionar la que más se adecue a las condiciones reales de realización por parte de la empresa.

Todos los valores que se requieren para poder elaborar la secuencia de los trabajos responden a una serie de operaciones obtenidas, para poder fabricar la pieza, por los tecnólogos utilizando técnicas de planeación de procesos.

Ejemplo de proceso: Fabricación de excéntrica para dispositivos de conformado del arco

1. Se identifican las operaciones a realizar: corte de material con segueta, torno y recortador. Estas operaciones responden a cada una de las etapas.

2. Se caracterizan los trabajos que se realizarán:

3. Otros aspectos técnicos como son: tipo de material de la pieza a elaborar, maquinabilidad, tipo de elaboración, uso de refrigerantes, etc, se integran al problema mediante los tiempos debidos a la secuenciación y al cambio de operación en correspondencia con la carta tecnológica, ya diseñada.

4. Los datos correspondientes a este caso son:

Tiempos de procesamiento unitario de cada trabajo (min)

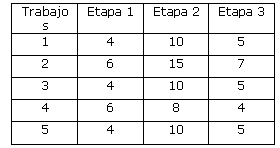
Velocidades de las máquinas por etapas (m/min)

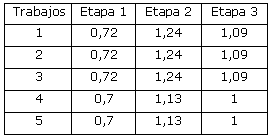
Tiempo de preparación entre máquinas (min)

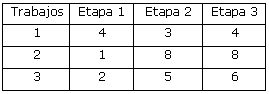
Fecha de realización (min)

Tiempo de preparación entre secuencias (min)

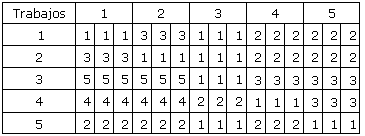
Una vez que se realiza la entrada de datos, se obtienen los siguientes resultados:

Salida de datos

Simulación de la población con número: 61

Tiempo de CPU para la obtención de sus parámetros: 8 segundos

Tiempo de procesamiento de cada trabajo en cada etapa (min)

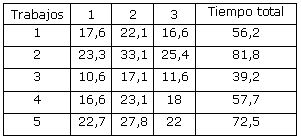
En otra evaluación del algoritmo implementado con el mismo juego de datos, solamente se varían algunos de los valores deseados para considerar el caso de la existencia de trabajos atrasados y se obtienen los siguientes resultados:

Salida de datos

Simulación de la población con número: 41

Tiempo de CPU para la obtención de sus parámetros: 8 segundos

Tiempo de procesamiento de cada trabajo en cada etapa (min)

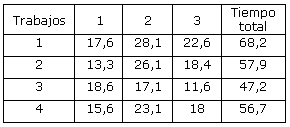
En ambos casos se obtienen secuencias de operaciones que responden a la problemática real de la empresa y que satisfacen las condiciones de trabajo, pues los tiempos de preparación que se utilizan tienen incorporados los problemas que se presentan en la acción diaria.

Desde el punto de vista del aspecto económico el algoritmo implementado está relacionado con los dos objetivos que conforman la función objetivo: el tiempo de completamiento de los trabajos y la cantidad de trabajos atrasados. La minimización de ambos objetivos influye sobre el salario del obrero directo, pues aunque no se incide sobre la cantidad de materiales que se gasta, si tiene influencia sobre maximizar la cantidad de producción, lo que conduce al aumento de los volúmenes de producción y por ende al aumento de los ingresos de la empresa.

Así mismo, la minimización de ambos objetivos incide sobre el costo, pues si disminuye el costo de operación asociado a la utilización de las mejores secuencias, en la cual se consideran los tiempos de preparación que se produce por el cambio de máquinas y el tiempo de preparación que se origina por la secuenciación de las operaciones, hay una incidencia real sobre los salarios y el costo indirecto, al ser estos función del tiempo de operación.

Al definirse las utilidades como la diferencia entre ingresos y costo, es evidente que al aumentar los ingresos y disminuir el costo, en sus componentes: costo variable y costo fijo, el cual viene asociado al costo indirecto, entonces hay un incremento de las utilidades, por lo que hay una mejoría en la componente económica y por lo tanto un aumento de la rentabilidad, que es una de las grandes necesidades de la industria, en particular la industria nacional que necesita de aumentos significativos en sus volúmenes de producción y en su rentabilidad.

Mediante la implementación del modelo y el algoritmo que se presenta en esta tesis, las secuencias que se obtienen a partir de la utilización de los datos reales permiten afirmar que hay un incremento de alrededor de un 2 % en la producción al ser utilizadas las mejores secuencias obtenidas, lo cual incide en el aumento de la eficiencia de los procesos productivos de los talleres a partir de la conciliación de las secuencias de trabajo en dichos talleres.

En particular, para el caso que se analiza la utilización de las secuencias que resultan del modelo que se implementa contribuyen a disminuir en 1,35548 unidades monetarias el gasto para producir una pieza, por lo que si además aumenta la cantidad de piezas producidas en x unidades, se tiene entonces que la disminución es igual a 1,35548 x unidades monetarias y el ingreso aumenta en similar magnitud y por ende las utilidades de la empresa.

La implementación en la industria de un programa de fabricación que mejore el tiempo de procesamiento total y la cantidad de trabajos atrasados implica la reducción de la duración total del proceso, lo que influye positivamente en el ahorro energético con una reducción del consumo de combustible, con los altos precios que presentan en la actualidad, además de reducir también la carga contaminante para la atmósfera.

Además, con la selección de una secuencia adecuada en la fabricación de pedidos consecutivos de una misma pieza, se eliminan los tiempos de preparación, lo cual conlleva a eliminar la necesidad de detener para limpiar la máquina o los moldes o cualquier otro componente necesario, eliminando la generación de cantidades de residuos y por ende la necesidad de su almacenamiento o de tratamiento.

Así mismo, contribuye a una utilización racional del transporte de carga, debido a la posibilidad de que los trabajos no se atrasen y disminuyan los viajes innecesarios, con el consabido gasto de combustible y emisiones de gases nocivos.

Finalmente, el hecho de disponer de una herramienta informática para establecer los programas de producción puede implicar la no necesidad de un soporte físico para los datos y cálculos, con la consiguiente reducción en el consumo de papel.

CONCLUSIONES

• La implementación computacional del modelo resultó ser efectiva y competitiva con respecto a otro método reportado en la bibliografía y permitió validar convenientemente el algoritmo metaheurístico híbrido elaborado; este requiere, como regla, de menos tiempo para proponer una selección de las mejores secuencias para que puedan ser seleccionadas por el decisor.
• Las experiencias realizadas en la industria muestran la factibilidad de la introducción en explotación del algoritmo desarrollado, para lo que se requiere del desarrollo de un software profesional con este fin.
• Se permite la presencia en los tiempos de procesamiento de los artículos en las máquinas valores iguales a cero, lo cual permite incluir piezas que no requieran del procesamiento en determinadas etapas de producción, lo que da la posibilidad de mayor flexibilización en el flujo, ya que los artículos pueden pasar de una máquina a otra manteniendo las características del taller de flujo.
• La implementación realizada del algoritmo propuesto para su validación experimental permite el cálculo del tiempo que se necesita para la solución del problema y desde el punto de vista computacional, el haber sido desarrollado sobre el lenguaje C++ da posibilidades para realizar mejoras en su programación.

 

REFERENCIAS

1. ARZOLA RUÍZ, J. Sistemas de Ingeniería. La Habana: Editorial Félix Varela, 2000.

2. ARZOLA RUÍZ, J.; SIMEÓN, R. E., et al. El Método de Integración de Variables: una generalización de los Algoritmos Genéticos. En Optimal Design of Materials and Structures. París, Francia. 2003.

3. GLOVER, E, KELLY, J.P y LAGUNA, M. "Genetic algorithms and tabu search. Hybrids for optimization". Computers and Operations Research
vol. 22, nº 11, 1995.

4. LAGUNA, M Y MARTÍ, R. Scatter Search: Methodology and Implementations in C. Kluwer Academic Publishers. 2003.

5. Universidad de Porto. Programación de pedidos en un taller con máquinas en paralelo y tiempo de preparación. Oporto, Portugal: Universidad de Porto. 2005.

6. Rajendran, C. y Ziegler, H. "Scheduling to minimize the sum of weighted flow time and weighted tardiness of jobs in a flow shop with sequence-dependent setup times". European Journal Operational Research. vol. 149(3). 2003.

Recibido el 20 de noviembre de 2009
Aceptado el 26 de febrero de 2010