Introducción
El proceso de soldadura CMT se basa en una modificación del proceso de soldadura con alambre metálico fusible y protección gaseosa (GMAW), cuyo calor de entrada puede ser relativamente bajo, en comparación con el proceso de ignición del arco convencional GMAW [1]. La palabra fría, en el nombre del proceso CMT, representa un término que sugiere la nueva forma de transferencia de las gotas del alambre de aporte (con baja intensidad de corriente).
El proceso CMT lo distinguen dos características fundamentales: a) el movimiento reciprocante del material de aporte; b) la transferencia de metal es casi libre de corriente [2,3].
En el proceso CMT la alternancia de los ciclos de corriente y tensión modifica la amplitud de sus respectivas ondas que, unidas con la oscilación del avance y retracción periódica del electrodo, convierten el aporte térmico del proceso en un ciclo alterno, en rangos de valores extremos máximos (Qmáx) y mínimos (Qmín) [4].
Igualmente, puede estimarse que el calor transferido a la unión soldada produce variaciones cíclicas en las temperaturas del baño de soldadura y en las posiciones del límite de fusión. La variación de la posición del límite de fusión puede producir fluctuaciones en las dimensiones de la zona fundida; es decir, en las dimensiones geométricas del baño de soldadura (ancho y profundidad de penetración, fundamentalmente).
Este aspecto es tratado por Azar [5] y Pérez [6], al proponer ambos modelos que pretenden explicar el comportamiento del modelo de fuente de calor doble elipsoidal desarrollado precedentementepor varios autores [7-9] para la simulación del calor introducido en soldadura, pero aplicado al proceso CMT.
La propuesta de Azar [5] se sustenta en la introducción de una integral de línea definida, en el modelo de fuente de calor doble elipsoidal de Goldak [7], dentro de la que se incorporan ecuaciones sinusoidales modulares, que simulan la variación de los parámetros geométricos de la poza de fusión.
La integral de línea definida propuesta por Azar [5] no establece respecto a qué variable se realiza la integración. La introducción simultánea de la integral de línea y de las funciones para la variación de todos los parámetros energéticos y geométricos altera el efecto real del calor introducido en la soldadura.
Por otra parte,Pérez [6] introduce una modificación eliminando la integración del modelo de Azar y variando los términos modulares en la forma sinusoidal de la fluctuación de los parámetros geométricos y de entrada de calor. Sin embargo, el efecto del módulo en las ecuaciones sinusoidales, referentes a los parámetros geométricos y a la energía, resuelve el problema de evitar valores negativos en los resultados estudiado por Pérez, pero tergiversan los valores reales.
Los modelos de fuente de calor publicados hasta el momento [10,11], no caracterizan suficientemente el comportamiento real de las oscilaciones de las dimensiones geométricas de los cordones, ni del aporte térmico, obtenidos de la aplicación del proceso de soldadura CMT.
Un análisis matemático sobre funciones seriadas y su extrapolación a la descripción de fenómenos cíclicos permitiría reevaluar las soluciones planteadas por Azar [5] y Pérez [6], para la simulación de la variación de la función del modelo de fuente de calor de Goldak, tal que se aporta un modelo matemático que se ajusta al comportamiento de los parámetros geométricos de la zona de fusión obtenida con la aplicación del proceso de soldadura CMT.
Por tal motivo, el objetivo del presente trabajoesestablecer un modelo matemático de fuente de calor que describa el comportamiento de las secuencias sinusoidales de solidificación de las ondulaciones superficiales correspondiente a los parámetros geométricos del baño de soldadura y de la fuente de calor en el proceso por transferencia metálica fría.
El modelo establecido encuentra aplicacionesen la determinación de los ciclos térmicos durante la ejecución del proceso de soldadura CMT sobre cualquier material, además de permitir estudiar la influencia de los campos térmicos sobre las deformaciones mecánicas producidas por las tensiones residuales y las transformaciones de fases en la pieza a soldar, de una forma más cercana a la realidad.
Métodos y Materiales
La energía térmica efectiva (Q efect ) aportada por la potencia del arco es directamente proporcional a las fluctuaciones instantáneas de la corriente (i) y el voltaje (u) aplicados en el proceso de soldadura CMT y se corresponde con el ciclo de desplazamiento (alimentación - retracción) del electrodo y de deposición de las gotas de metal.
Entonces, el ciclo de la onda energética (Q efect ) del proceso CMT puede aproximarse, también,a la evolución completa de una onda sinusoidal alterna variable con el tiempo y, de formasimilar, la onda característicaque representa eldesplazamiento del electrodo.
Luego, por analogía con la onda de desplazamiento del electrodo, puede establecerse la expresión instantánea de la onda sinusoidal que sufre la energía FQ
(t)
, ecuación 1, como una función directa y sinusoidal, que depende de la amplitud de la onda sinusoidal (
La frecuencia (f) del proceso CMT puede considerarse aproximadamente de 60 Hz o ciclos por segundo. La velocidad angular (ω) de la onda característica del proceso CMT representa el número de radianes (o grados) recorridos del electrodo en la unidad de tiempo, ecuación 2.
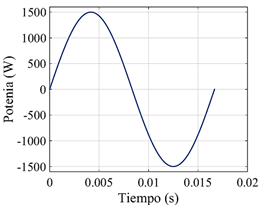
El ciclo mostrado posee valores, tanto positivos, como negativos, figura 1. Si bien, el ciclo de alimentación del alambre se corresponde con una onda sinusoidal sin valores negativos, aunque exista retracción del alambre de soldadura, la energía introducida tampoco puede tener valores negativos.
Si se considera que la contracción mínima de la energía FQ (t) , nunca debe tener valores inferiores a cero, ha de restringirse la función, con un mínimo (Q mín ≥ 0), ecuación 3.
De esta forma la onda que sufre el parámetro energético (Q) podría expresarse como una función periódica positiva, para todo el dominio de tiempo evaluado.
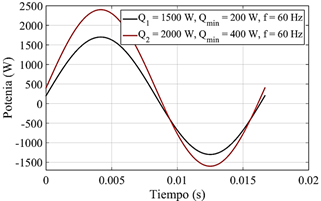
La onda sinusoidal se amplifica al introducirse el parámetro amplitud (Q), volviendo a alcanzar valores negativos; tanto mayores, cuanto lo sea el valor del parámetro amplitud.Además, la ecuación 3 desfasa el cruce por cero en dependencia del valor de Q min , figura 2.
Con la introduccióndel módulo para el cálculo de la ecuación 4, se elimina el efecto negativo de la sinusoide sobre los parámetros evaluados, pero los valores mínimos y máximos se distorsionan
En caso de que se evaluaran para Q max = 1500 W y Qmín = 200 W se obtienen valores de (FQ (t) ), que caracterizan con similar precisión a los extremos de la función graficada según la figura 3.
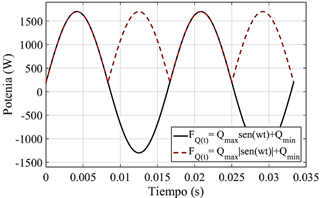
Fig. 3 Efecto de la rectificación (obtención de valores modulares) de la funciónFQ (t) =Q·sin(ω·t)+Q mín ; f = 60 Hz
La función seno puede desplazarse en el eje de las ordenadas, a partir de la introducción de coeficientes en la amplitud y el valor mínimo, ecuación 5. Esto permite la no obtención de valores negativos en las magnitudes dimensionales de la geometría del cordón, ni de la energía aportada, manteniendo la frecuencia de ocurrencia del proceso, ecuación 5
De la ecuación 5, aplicada a la descripción de las variaciones de la energía aportada por el proceso CMT, puede obtenerse un comportamientosinusoidal, siempre positivo, figura 4, enmarcado entre los valores máximos (Q máx ) y mínimos (Q mín ). Esta función describe matemáticamente la variación del parámetro Q respecto al tiempo (F Q(t) ).
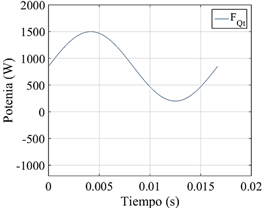
Fig. 4 Modelo propuesto para evaluar la potencial fluctuación de la potencia de arco en el proceso CMT (f = 60 Hz)
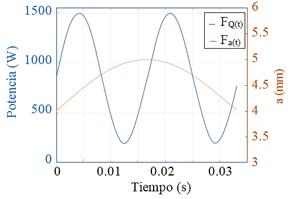
En los procesos de soldadura, los momentos de solidificación ocurren repetidas veces; tantas, como porciones del metal fundido se solidifican consecutivamente detrás del arco, toda vez que la porción del metal se encuentre en las condiciones termodinámicas adecuadas, lo que da lugar a ondulaciones superficiales. La frecuencia de solidificación (f s ) o del ciclo de formación de las ondulaciones superficiales del baño se puede estimar ente 5 y 10 veces menor que la frecuencia eléctrica (f d = 60 Hz) del proceso de soldadura. Para el caso del proceso CMT puede estimarse las frecuencias de solidificación (f s ) entre 11 Hz y 37 Hz, con períodos aproximados de 0,089 s y 0,027 s, respectivamente, figura 5, pudiéndose estimar para este proceso que la frecuencia de solidificación (f s ) puede ser entre 5,4 y 1,6 veces menor, que la frecuencia del ciclo de deposición de material (f d ) de solidificación (f s ).
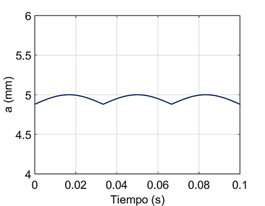
Fig. 5 Estimación de la variación del borde del cordón (del semiancho del cordón (a)), considerando una frecuencia de solidificación (f s =30 Hz)
La ecuación (Fa (t) ), que describe el comportamiento del límite de fusión o semiancho del cordón (a), puede expresarse (ecuación 6), a diferencia de la ecuación de la energía, con un núcleo modular en la sección sinusoidal, pero con el valor de la amplitud dada por la media entre los valores máximos (a máx ) y mínimos (a mín ) de la oscilación del semiancho del cordón (a).
En correspondencia con el estudio antes expuesto, se propone un modelo matemático, ecuaciones 7 y 8, basado en las secuencias sinusoidales independientes de la fuente de calor en soldadura, ecuación 9, y de solidificación de las ondulaciones superficiales, ecuaciones de la 10 a la 13, para el proceso CMT, que están en función de la frecuencia de ocurrencia de los procesos eléctricos (f d = 60 Hz) y térmicos (f s = 30 Hz), respectivamente.
Donde: f d , es la frecuencia de ocurrencia de los eventos eléctricos y de deposición de las gotas metálicas, para CMT que oscila entre 60 y 120 Hz;f s , es la frecuencia de solidificación o del ciclo de formación de las conchas del cordón, para CMT oscila entre 11 y 37 Hz;t, es el tiempo (s);a máx , b máx , c fmax , c rmax , son los valores máximos o amplitudes del semiancho (a), profundidad de penetración (b), longitud delantera (c f ) y trasera (c r ) del baño de fusión, respectivamente, en milímetros;a min , b min , c fmax , c rmax , son los valores mínimos de las dimensiones del semiancho (a), profundidad de penetración (b), longitud delantera (c f ) y trasera (c r ) del baño de fusión, respectivamente, en milímetros;Q max , Q min , son los valores máximos (amplitud) y mínimos de la energía de entrada (W·m-3).
Los valores máximos o de amplitud (Q max ) de la energía de entrada (W·m-3) y mínimos (Q min ) dependen de la combinación de los parámetros eléctricos de corriente máxima (I máx ) y mínima (I mín ) y de la tensión máxima (U I máx ) y mínima (U mín ) aplicados, ecuaciones 14 y 15, respectivamente, y de la eficiencia del arco (η) durante el proceso.
Las fracciones instantáneas tiempo-dependientes delanteras (f´ f ) y traseras (f´ r ) pueden ser calculadas geométricamente, ecuación 16, dependiendo de la sección que se trate (delantera o trasera) a partir de las variaciones de los parámetros geométricos del cordón.
Resultados
Para evaluar el comportamientodel modelo propuesto, se toman los resultados de las pruebas experimentales reportadas en [6], seleccionándose los parámetros reportados en la tabla 1. El valor del calor introducido por el proceso CMT (Q min , Q max ) está influenciado por un 85 % de eficiencia de la fuente de energía.
Tabla 1 Parámetros representativos del modelo propuesto
| Parámetro | Valor (mm) | Parámetro | Valor (mm) |
|---|---|---|---|
|
|
5 |
|
4,88 |
|
|
4 |
|
3 |
|
|
10 |
|
9 |
|
|
5 |
|
4 |
|
|
60 Hz |
|
0 W |
|
|
30 Hz |
|
1500 W |
Para simular la distribución de la densidad de potencia se emplea el software de programación MatLabR2016a. Se generan los gráficos tridimensionales correspondientes a los vectores de las matrices de línea (x, y, q f , q r ),con una dimensión de 1000,y representado en forma de superficie.
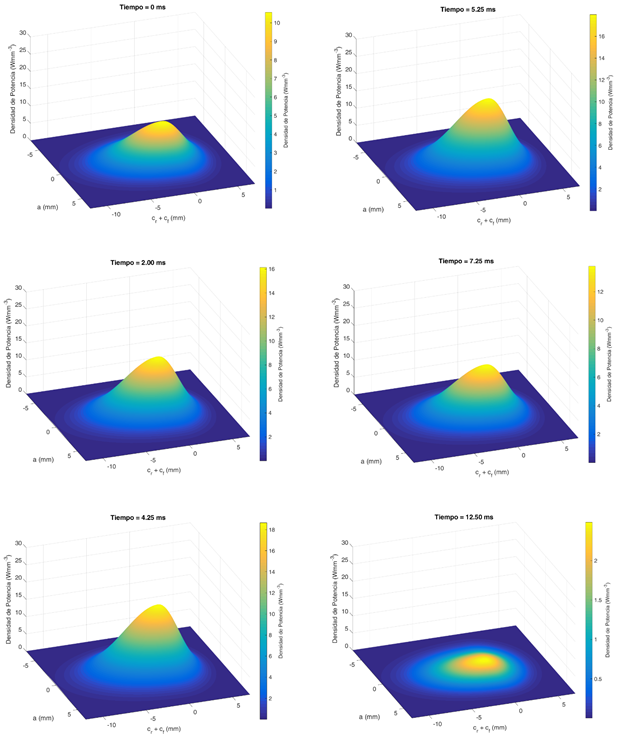
Para simular el ciclo de soldadura CMT, se considera el tiempo necesario para completar un ciclo o el período (T) de la onda de recorrido del electrodo de 0,01250 s.La variación de la densidad de potencia se simula entre 0 y 0,0125 s. Se obtiene una secuencia de gráficos superficiales en un dominio rectangular, figura 6.
Discusión
El proceso de soldadura CMT puede describirse, según se observa en la figura 6. Al inicio del periodo la fuente de calor representa los valores mínimos de densidad de potencia, coincidiendo con la ignición del arco eléctrico. Entre 0 ms y 4,25 ms el arco eléctrico alcanza la máxima densidad de potencia y el alambre electrodo se encuentra en la posición de extensión mínima (máxima longitud, desde la pieza hasta la boquilla). En este punto, la fuente de energía comienza a reducir la potencia y al mismo tiempo se desactiva el mecanismo retráctil del electrodo, acercándolo a la pieza, apreciándose una disminución del volumen de calor. En este momento se constata un decremento periódico de la densidad de potencia, se extingue el arco eléctrico y se deposita la gota de metal transcurridos12,5 ms. Culminado este ciclo se reactiva el mecanismo retráctil del alambre, reanudándose nuevamente el proceso, hasta finalizar la soldadura.
Desde el punto de vista energético, la figura 6 muestra que el voltaje y la corriente máximos comenzarán a disminuir, según lo definido por la forma de la onda sinusoidal alrededor de 4,25 ms, correspondiente al inicio de la disminución del proceso de ionización del arco eléctrico. Como consecuencia de la inductancia y la característica Volt-Ampérica de la fuente de potencia, el arco no se extinguirá instantáneamente. La energía de ionización de la fuente de energía comienza a disminuir siguiendo la forma de la onda sinusoidal que rige el modelo matemático y la columna se contraerá. Hasta este punto, no se aprecian variaciones en la dimensión de la fuente de calor.
A partir de los 2 ms, se produce el proceso de formación de la gota, que finaliza a los 4,25 ms con la extinción del arco eléctrico. Entre 10 y 12,5 ms, la entrada de calor alcanza sus valores mínimos y el flujo de calor disminuye y se produce la deposición de la gota de metal durante el cortocircuito. El tiempo transcurrido de 8,25 ms, una vez extinguido el arco eléctrico,permite que la gota de metal formada en la punta del electrodo sea transferidaal baño de soldadura en un gradiente de temperatura menor. Sin embargo, nunca llega a cero el flujo de calor al final del evento de transferencia de la gota de metal fundido al baño de soldadura, figura 6.
Los parámetros geométricos del modelo de fuente de calor controlan la dimensión del baño de soldadura.
En un análisis dimensional de las funciones del modelo de fuente de calor para el proceso de soldadura CMT propuestas por Azar [5] puede constatarse que no es consistente, al obtenerse su resultado con valores cuadráticos.
Por otra parte, el efecto producido por la introducción del módulo completo en las funciones sinusoidales referente a los parámetros geométricos y en la energía, según estudios realizados por Azar [5], no replica fielmente el comportamiento cíclico del proceso CMT.
La introducción del valor mínimo (Qmín) no resuelve el problema de los resultados negativos de la función y, por tanto, tampoco el ajuste al problema real; al menos con los valores máximos (Qmáx) y mínimos (Qmín) establecidos, volviendo a alcanzar valores negativos; tanto mayores, cuantolo sea el valor del parámetro amplitud.
Pérez et al. [6] introducen una mejora del modelo para simular el proceso de soldadura CMT consistente en un módulo parcial, modificando las funciones propuestas por Azar [5]. La introducción del módulo parcial, resuelve el problema dimensional y conduce a la rectificación de la onda, suponiendo, por ejemplo, el nivel mínimo en Q mín = 200 W, mayor que cero, y la amplitud en Q = 1500W. Al aplicar este modelo modular parcial solamente a la parte sinusoidal de la función (FQ (t) = Q·│sin(ω·t)│+ Q mín ), pero para los parámetros mínimos (Q min =200 W) y de amplitud (Q = 1500 W), se obtienen valores de la función semiancho del cordón (FQ (t) ) que caracterizan con similar precisión a los extremos de la función. Esto prueba que es más recomendable emplear el modelo modular parcial aplicado solamente a la parte sinusoidal de la función, que no el completo presentado por Azar.
Sin embargo, la onda obtenida con el módulo colocado solo en la función sinusoidal no posee un comportamiento simétrico en sus puntos de inflexión máxima y mínima.
Además, modular parcialmente la parte sinusoidal de la función reduce el período de la onda a la mitad, duplicando su frecuencia y su velocidad angular.
Azar [5], al emplear el módulo de la función, también emplea el valor de la velocidad angular solo como el producto π·f. Esta consideración reduce a la mitad (189 radianes·s-1) la velocidad angular real (377radianes·s-1). Este aspecto presupone la disminución a la mitad (T = 0,00834 s) el período de funcionamiento real (T = 0,01667 s) del proceso y, por tanto, del incremento (al doble) del número de ciclos (f = 120 Hz), lo cual no se ajusta al valor real de la frecuencia (60 Hz) del proceso CMT.
La no coincidencia de la frecuencia de operación (120 Hz) de la función modular completa con la del funcionamiento real del proceso (60 Hz), puede conducir a evaluar como aproximado el modelo propuesto por Azar.
A diferencia del modelo propuesto por Azar [5] en el presente trabajo,las dimensiones de la fuente de calor, que corresponden al baño de fusión, no disminuyen con la misma frecuencia que la densidad de potencia.Obsérvese que la frecuencia (f s ) de ocurrencia del evento (solidificación de la zona del baño de fusión) es diferente a la de ocurrencia de los eventos eléctricos, figura 7.
La oscilación de la superficie libre en el borde externo del baño de fusión (a) determina la ondulación de la superficie solidificada, la cual se verifica cada 3,3 10-3 s. Para un periodo registrado de 3,3 10-3 s, que describe la variación de las oscilaciones del baño de soldadura en el proceso de formación de las ondulaciones superficiales debido al ciclo de solidificación, se verifican dos ciclos de transferencia de metal, figura 7.
Estas ondulaciones superficiales pudieran estar asociadas a la profundidad de penetración de la zona de fusión producto de la variación de los parámetros eléctricos del proceso de CMT, tales como la corriente, la tensión, las correcciones de pulso, longitud de arco y la velocidad de soldadura.
Al aumentar la frecuencia eléctrica del proceso a 120 Hz y aumentar la frecuencia de solidificación a 37 Hz, disminuyendo la velocidad de soldadura,durante la simulación,semejora notablemente la rugosidad del cordón debido a la producción de ondulaciones superficiales más unidas, figura 8. Sin embargo, al aumentar la velocidad de soldadura se pueden obtener ondulaciones más gruesas.
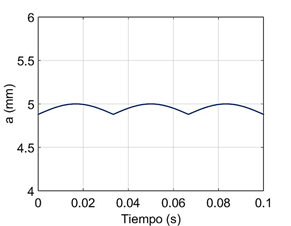
Fig. 8 Estimación de la variación del borde del cordón (del semiancho del cordón (a)), considerando una frecuencia de solidificación (f s = 37 Hz)
El modelo de fuente de calor propuesto para la soldadura CMT se ajusta a un ciclo ideal sinusoidal de energía aportada, dependiente de la frecuencia de los procesos eléctricos y de deposición de las gotas durante la transferencia de metal, de la oscilación dimensional del baño fundido y de la frecuencia de solidificación.
En la modelación se estima que las funciones sinusoidales modulares, que describen el comportamiento de ciclos de variación positiva del semiancho (a) del cordón de soldadura, su profundidad de penetración (b) y sus longitudes, tanto delantera (c f ), como trasera (c r ) de la zona de fusión, son coincidentes con la frecuencia, simetría y la ocurrencia de máximos y mínimos, producidos durante el comportamiento esperado de los ciclos en el proceso de solidificación del metal de las uniones soldadas con el proceso CMT.
La frecuencia (f d ) del ciclo de deposición de material o eléctrico, durante el proceso de soldadura CMT, no coincide con la frecuencia de solidificación (f s ) del ciclo de formación del cordón. Este fenómeno no es solo exclusivo del proceso CMT, sino que es común para todos los procesos de soldadura por arco, con o sin aporte metálico. La frecuencia de solidificación empleada para evaluar las dimensiones del cordón de soldaduradepende de la velocidad de soldadura y de la potencia eléctrica empleada en el proceso CMT.
El modelo de fuente de calor doble elipsoide oscilatorio que se desarrolla, se limita a la aplicación de la simulación de los cíclos térmicos, las tensiones y deformaciones residuales y las transformaciones de fase durante la soldadura empleando el proceso CMT, lo cual pudiera extrapolarse a otros procesos de soldadura por arco previa validación experimental.
Conclusiones
El modelo energético doble elipsoidal oscilatorio propuesto para soldadura por arco con transferencia metálica fría considera las fluctuaciones de las diferentes frecuencias sinusoidales de los parámetros eléctricos del arco y solidificación del baño de soldadura, sobre la simulación de la densidad de potencia transferida al material base.
El modelo desarrollado particulariza los valores de las frecuencias y mejora su tratamiento matemático permitiendo simular con mayor precisión la influencia de la densidad de potencia transferida al material base en el proceso de soldadura por arco con transferencia metálica fría.