Artículo Original

Algoritmo para el cálculo de la mantenibilidad usando la distribución gamma empleando el método de grafos dicromáticos

Algorithm to assess the maintenance using gamma distribution employing dicromatic graph

Reinaldo Ihosvanny Benítez-Montalvo^{I  *}  , Armando Díaz-Concepción^II  , Sergio Marrero-Osorio^III  , Alejandro Romero-Vega^III  , Leisis Villar-Ledo^IV  , Roberto García-Ramírez^V  , Jorge Enrique Tamayo-Mendoza^VI 

^I Centro de Inmunología Molecular. La Habana, Cuba

^II Universidad Tecnológica de la Habana, Centro de Estudios en Ingeniería de Mantenimiento. La Habana, Cuba

^III Universidad Tecnológica de la Habana, Facultad de Ingeniería Mecánica. La Habana, Cuba

^IV Universidad Tecnológica de la Habana, Facultad de Ingeniería Industrial. La Habana, Cuba

^V LATAMCONTROL S.L. Madrid, España

^VI Universidad Técnica de Manabí,.Manta, Ecuador

Resumen

El presente trabajo tuvo como objetivo diseñar un algoritmo para el cálculo de la mantenibilidad empleando el método de los grafos dicromáticos usando los parámetros de forma y escala de la distribución gamma, estimados a partir del método de aproximación de Thom. Para esto se utilizó el sistema para la solución de problemas de cómputo basado en el Método de los Grafos Dicromáticos. Las variables de entradas son el número de elementos no nulos, tiempo dereparación y el tiempo medio para reparar, con ellos se identifica el tipo de distribución. A partir de la síntesis de los grafos partiendo del modelo, se obtiene un algoritmo de cálculo que permite evaluar la mantenibilidad a partir del tipo de distribución de la data colectada. El algoritmo de cálculo obtenido permitió evaluar la mantenibilidad de las distribuciones más comunes en el cálculo de la mantenibilidad (normal, exponencial y Weibull) de forma más expedita que los métodos tradicionales.

Palabras-clave: grafos dicromáticos; distribución gamma; mantenibilidad; algoritmo; método de aproximación de Thom; sistema computacional

Abstract

To design an algorithm for the calculation of maintainability using the dichromatic graph method was the objective of this research which was done using the shape and scale parameters of the gamma distribution, estimated from Thom's approximation method. For that porpose, the system for the solution of computation problems based on the Dichromatic Graph Method was used. The number of non-zero elements, the repair time and the average time to repair were the input variables, identifying with them the type of distribution. From the synthesis of the graphs starting from the model, a calculation algorithm is obtained that allows to evaluate the maintainability from the type of distribution of the data collected. The calculation algorithm obtained was used to evaluate the maintainability of the most common distributions in the maintainability calculation (normal, exponential and Weibull) more expeditiously than traditional methods.

Key words: dichromatic graphs; gamma distribution; maintainability; algorithm; Thom’s approximation method; computational system

Introducción

La mantenibilidad como elemento integrante de la confiabilidad operacional e indicador de la gestión de mantenimiento es una función estadística que puede responder a varias distribuciones. Para evaluar este indicador es imprescindible conocer el tipo de distribución que siguen los tiempos de reparación, variable objeto de este estudio. Los métodos empleados para este fin comprenden los métodos estadísticos (paramétricos) y grafico-analítico (ajuste de la distribución).

La identificación del tipo de distribución por métodos estadísticos exige el uso de softwares especializados como el Statgraphic y otros, mientras que el grafico-analítico requiere de papel logarítmico o funciones empíricas donde el coeficiente de determinación de mayor valor representa la función. Este último tiene como desventaja que solo permite escoger entre dos funciones. La caracterización de la distribución a través de los parámetros de forma y escala de la distribución gamma estimados por el método de aproximación de Thom fue propuesta por ^[1]. Hasta el presente, el uso de la distribución gamma solo se limita al estudio de las variables meteorológicas ^[2]. Dado que fue demostrada la validez del método de aproximación de Thom en la personalización de las distribuciones normal, exponencial y Weibull, funciones más usadas en el cálculo de la mantenibilidad, se propone elaborar un algoritmo de cálculo a partir del mismo para evaluar este indicador.

Gasca 2017 ^[3] en su investigación recomienda un procedimiento para el cálculo de la mantenibilidad pero se basa en la prueba de distribuciones y el empleo de métodos clásicos de cálculo lo cual lo hace engorroso.

Gallegos 2018 ^[4] plantea elementos para el cálculo de al mantenibilidad siguiendo lo planteado el método de correlación para identificar el tipo de distribución lo cual continua siendo extenso en su implementación.

Los grafos dicromáticos permiten aprovechar las particularidades teóricas de los grafos dicromáticos durante el proceso de solución del problema, pasando por un proceso rigurosamente ordenado a partir de la caracterización del problema y su correcta formulación hasta la obtención del algoritmo ^[5, ^6].

La investigación tuvo como objetivo diseñar un algoritmo para el cálculo de la mantenibilidad empleando el método de los grafos dicromáticos usando los parámetros de forma y escala de la distribución gamma. Para dar cumplimiento se utilizó el sistema para la solución de problemas de cómputo basado en el Método de los Grafos Dicromáticos. El algoritmo obtenido permite evaluar la mantenibilidad de las distribuciones más comunes en el cálculo de la mantenibilidad.

Métodos y Materiales

Para desarrollar este trabajo se utilizó un modelo matemático el cual describe las ecuaciones que intervienen en el cálculo de la mantenibilidad y los métodos la forma de obtención de los valores de los parámetros de selección, selección del tipo de distribución y por último el algoritmo que describe la secuencia de cálculo y tres métodos:

• Método de aproximación de Thom.

• Método de estimación de las funciones normal, exponencial y Weibull a partir del método de aproximación de Thom.

• Método de Grafos Dicromático.

Modelo matemático para el cálculo de la mantenibilidad

Para la obtención del modelo matemático se utilizó como base las ecuaciones 1, 2, 3, y 4 propuestas por Thom para estimar los parámetros de forma y escala de la distribución gamma. La ecuación 4 representa una ecuación empírica propuesta por el mismo a fin de considerar solo los valores no nulos en el cálculo del algoritmo.

Tanto las ecuaciones restantes 5 - 10, como las condiciones necesarias para identificar el tipo de distribución en función de los parámetros de forma y escala ^[10-^12], la función mantenibilidad y la varianza se programaron en el resolvedor matemático TK Solver.

$\alpha =\frac{1}{4A}\left(1+2\sqrt{(1+\left(\frac{4A}{3}\right)}\right)$ (1)

$A=ln\overline{MTTR}-\sum \frac{lnTTR}{p}$ (2)

$\beta =\frac{\overline{MTTR}}{\alpha }$ (3)

$p=n-q$ (4)

$MTTR=\frac{\sum TTR}{p}$ (5)

$Mt=e^{-t/MTTR}$ (6)

$Mt=e^{{\left(\frac{t}{\beta }\right)}^{\alpha }}$ (7)

$Mt=\frac{1}{2.5*s}*e^{-\left(\frac{{\left(t-MTTR\right)}^2}{2*s^2}\right)}$ (8)

$s=\sqrt{\frac{\sum y}{n-1}}$ (9)

$y={\left(TTR-MTTR\right)}^2$ (10)

Donde:

α:	parámetro de forma (adimensional)
β:	parámetro de escala (adimensional)
q:	número de elementos nulos en el periodo que se analiza (adimensional)
P:	número de fallos en el periodo que se analiza (adimensional)
n:	total de elementos de la muestra en el periodo que se analiza (incluye los nulos) (adimensional)
TTR:	tiempo de reparación del activo (horas)
MTTR:	tiempo medio para reparar (horas)
A:	relación entre logaritmo de la media y la media del logaritmo.
t:	tiempo para reparar programado (horas)
dist:	distribución(Exponencial, Weibull y Normal)
Mt:	mantenibilidad (%)
x-	lista que contiene la diferencia de cuadrados para el cálculo de la varianza (horas)
y-	lista que contiene los tiempos de reparación del activo (horas)
s-	varianza (adimensional)

Métodos aplicados en la investigación

• Método de aproximación de Thom ^[8]. Consiste en determinar a través de tres ecuaciones los parámetros de forma y escala de la distribución gamma: α, A y β.

• Método de estimación de las funciones normal, exponencial y Weibull a partir del método de aproximación de Thom ^[2].Con este método se establecen los valores de los parámetros de forma y escala que permiten identificar el tipo de distribución.

• Método de Grafos Dicromáticos con base en el sistema para la solución de problemas de cómputo: Permite obtener un algoritmo de cálculo a partir de las ecuaciones que caracterizan el problema a resolver (cálculo de la mantenibilidad) y de las variables de entrada y salida ^[8].

Resultados y Discusión

Tomando como base lo establecido en los métodos de la investigación y en lo específico las ecuaciones del sistema se obtiene:

Caracterización del problema

El modelo matemático que describió el cálculo de la mantenibilidad consta de 13 variables y 10 relaciones (ecuaciones). Las variables se distribuyeron como se muestra a continuación:

Variables de entrada

q , TTR, t

Variables de salida

y, s, Mt, β, α, A, p, n, dist, MTTR

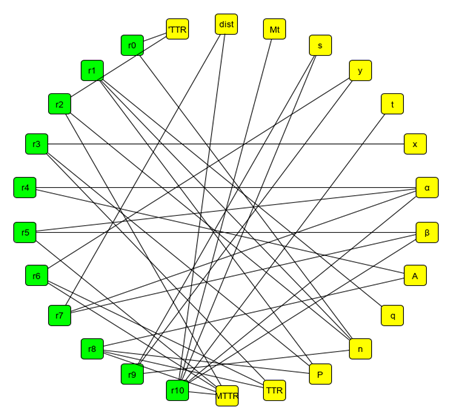
En la figura 1 se muestra el grafo del modelo que se genera a partir del conjunto de relaciones matemáticas que describen lo que ocurre físicamente en el caso analizado.

Fig. 1 Grafo del modelo 

Grafo del problema

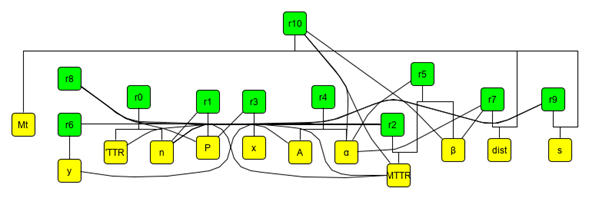
Partiendo del grafo del modelo, cuyos vértices representan las variables con un color y las ecuaciones (relaciones) con otro y las aristas simbolizan cuáles variables se encuentran en cada ecuación, figura 2.

Fig. 2 Grafo del problema 

Los métodos empleados por ^[3, ^4] permiten suponer un tipo de distribución a partir de una función empírica según el coeficiente de determinación, seleccionar el que posea mayor valor por ser representativo de la función a partir del análisis realizado en una hoja de cálculo (Excel). Este método tiene como desventaja que solo permite seleccionar entre dos funciones. El método grafico constituye otra alternativa aunque con un trabajo más engorroso, con la misma desventaja que el anterior ^[9, ^10]. El programa estadístico Stargraphic deja la decisión al analista de seleccionar a partir de la tasa de error entre 16 o 32 distribuciones, pues solo se limita a mostrar si existe o no la correspondencia con la distribución norma. Este método permite de manera automática determinar el tipo de distribución eliminando las dificultades anteriores.

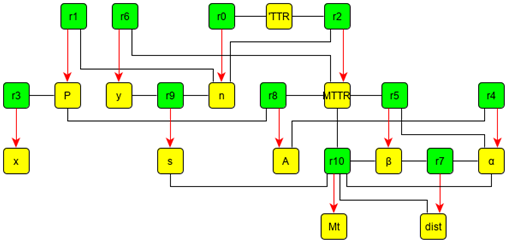
Grafo del problema pareado

Una vez planteado un problema de cómputo determinado, se descartan de dicho grafo las variables de entrada (datos), quedando transformado así en el grafo de la situación. A partir de este, suprimiendo las componentes conexas (islas) que no contengan variables de salida, se obtiene el grafo del problema; el cual es sometido a un pareo que orienta hacia su correspondiente variable a una sola de las aristas conectadas con cada ecuación, de modo que el mismo sea un pareo máximo, figura 3.

Fig. 3 Grafo del problema pareado 

A partir de lo anterior se obtiene una nueva representación llamada grafo del problema pareado. El problema pareado, tomando como base el modelo matemático anterior está compuesto por: un conjunto de variables de entrada y salida, dos incógnitas de control (y, MTTR), un pareo máximo 9, un problema compatible, determinado y realizable.

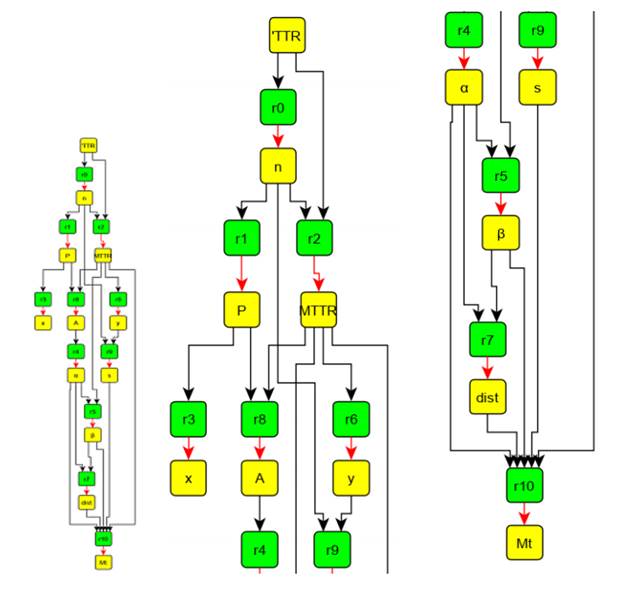
Algoritmo de cálculo

Posteriormente, se obtiene el grafo del resolvente, asignándole orientación, de variable a la ecuación, a las aristas que aún no la tienen. A partir de dicho resolvente (que ya se encuentra en su forma canónica) se alcanza el grafo del algoritmo descartando los caminos que no conducen a ninguna de las variables de salida definidas al plantear el problema ^[5, ^12] ver figura 4.

Fig. 4 Algoritmo de cálculo 

El algoritmo de cálculo obtenido para evaluar la mantenibilidad a partir del método de aproximación de Thom permite estimar los parámetros de forma y escala de la distribución gamma facilitó identificar las distribuciones más comunes (Normal, Exponencial y Weibull) a partir de los parámetros anteriores de manera más expedita que los empleados en las investigaciones por ^[9-^11]. Permite obtener directamente, previa obtención de los parámetros de forma y escala de la distribución gamma, la distribución de los datos sin recurrir al empleo de otro software estadístico empleado para este fin además de evaluar la mantenibilidad.

La limitación de este trabajo es que se restringe al uso de las 3 distribuciones más comunes en el cálculo de la mantenibilidad (Weibull, Normal y Exponencial)

Conclusiones

Se demostró que con el empleo de los grafos dicromáticos se obtuvo un algoritmo apoyado en el método de aproximación de Thom que simplifica los cálculos de la mantenibilidad, evitando el uso de los métodos tradicionales.

Referencias

1.  Benítez Montalvo RI, Díaz Concepción A, Rodríguez Piñero AJ, et al. Cálculo de la mantenibilidad usando la distribución gamma Ingeniería Mecánica. 2018;1(3):52-58.

2.  de Jesús Navar J. Estimaciones empíricas de parámetros de la distribución Weibull en bosques nativos del norte de México. Revista Forestal Latinoamericana. 2009;24(2):51-68.

3.  Gallegos Londoño C, Calderón Freire E, Cuzco Viscaino M, et al. Metodología para medir la mantenibilidad probabilística aplicada a grupos electrógenos. Perfiles. 2018;2(20)

4.  Gasca M, Camargo LL, Medina B. Sistema para Evaluar la Confiabilidad de Equipos Críticos en el Sector Industrial. Información Tecnológica. 2017;28(4):111-124.

5.  Rodríguez Puente R, Marrero Osorio S, Lazo Cortés MS. Algoritmo de reducción de grafos sin pérdida de información. Computación y Sistemas. 2014;18(1):185-194.

6.  Shi G, Chen W. A Graph Reduction Approach to Symbolic Circuit Analysis. In: Proceedings of the 2007 Asia and South Pacific Design Automation Conference. Yokohama, Japan: IEEE Computer Society; 2007. [Consultado 30 de septiembre de 2018]. Disponible en: Disponible en: http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4196031 6.

7.  Arroyo I, Bravo LC, Llinás H, et al. Distribuciones Poisson y Gamma: Una Discreta y Continua Relación. Prospect. 2014;12(1):99-107.

8.  Escalona Escalona Y, Romero Vega A, Marrero Osorio SA, et al. Sistema para la solución de problemas de cómputo basado en el Método de los Grafos Dicromáticos. Revista Internacional de Gestión del Conocimiento y la Tecnología. 2013;1(1):37-46

9.  Acosta J, Greiner C, Dapozo G . Herramienta para evaluar atributos de mantenibilidad en aplicaciones PHP. In: 15th Argentine Symposium on Software Engineering, ASSE 2014. Argentina: Sociedad Argentina de Informática (SADIO); 2014. [Citado 30 de septiembre de 2018] Disponible en: Disponible en: http://sedici.unlp.edu.ar/handle/10915/41674 9.

10.  Tarwani S, Chug A. Sequencing of Refactoring Techniques by Greedy Algorithm for maximizing Maintainability. In: Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India: IEEE; 2016. [Citado 4 de octubre de 2018] Disponible en: Disponible en: https://ieeexplore.ieee.org/abstract/document/7732243 10.

11.  Pérez González H, Martínez Pérez F, Nava Muñoz S, et al. Analizando la mantenibilidad de software desarrollado durante la formación universitaria. Revista Latinoamericana de Ingeniería de Software. 2015;3(6):231-236.

12.  Rodríguez Villalobos A. Grafos-Software para la construcción, edición y análisis de grafos. Madrid, España: Bubok Publishing; 2010.

Recibido: 13 de Febrero de 2019; Aprobado: 05 de Abril de 2019

^*Autor de correspondencia: [e-mail]