Introducción
La degradación de las propiedades de los dientes asociadas a traumas y enfermedades, es actualmente una de las problemáticas de la salud pública. Cuando faltan dientes ocurre la reabsorción del hueso alveolar. Para restaurar la función masticatoria, la estética y la fonética se incorpora una prótesis dental en sustitución de las piezas caídas [1, 2].
A comienzos del siglo XX se sientan las bases en la búsqueda del reemplazo de los dientes, apareciendo los implantes dentales, los cuales son un sustituto artificial de la raíz de un diente perdido. Habitualmente tienen forma roscada y están fabricados con materiales biocompatibles que permiten su unión al hueso [3].
Varios han sido los estudios realizados sobre los implantes dentales de aleaciones de titanio y cromo-cobalto [4, 5], incrementándose en las últimas décadas el interés por caracterizar su comportamiento a la fatiga mecánica; para lo cual habrá de prestarse especial atención a distintos factores como: las propiedades mecánicas de los materiales y las características geométricas de dichos implantes, en específico su rosca externa, por actuar como un concentrador de tensiones [6].
Esta situación de cargas cíclicas provoca que el fenómeno de la fatiga en implantes dentales sea un área de interés para los fabricantes, puesto que, aunque la tasa de éxito es muy elevada, algunos implantes pueden llegar a fracasar por fatiga.
Los pronósticos de durabilidad de los materiales utilizados en la fabricación de las prótesis dentales sometidos a fatiga, se hacen a partir de ensayos de laboratorio, donde finalmente se obtiene el comportamiento de las tensiones que son aplicadas con relación al número de ciclos de carga [7].
El objetivo del presente trabajo consiste en hacer un análisis del comportamiento a la fatiga de implantes dentales monocomponente, utilizando la modelación por elementos finitos y los modelos de la mecánica de la fractura.
Para lograr este fin, se tomaron como referencia nuevos diseños de implantes y los parámetros que se recomiendan según la norma ISO 14801 [8]. De este modo, se determinaron los valores de las tensiones equivalentes para el cálculo del número de ciclos de fatiga del implante y del factor de intensificación de tensiones durante el crecimiento de la grieta, hasta la rotura final.
Métodos y Materiales
Norma ISO 14801
Para evaluar la idoneidad de los diferentes diseños de implantes y componentes se realizan test de fatiga, definidos por la norma ISO 14801. Esta norma, titulada “Ensayo de fatiga para implantes dentales endoóseos”, especifica cómo se deben ensayar los implantes endoóseos de manera individual [8].
La misma establece un procedimiento general para realizar ensayos de fatiga a implantes dentales sencillos endoóseos, de tipo transmucosal y de sus componentes protésicos prefabricados. Este método resulta útil para la comparación de implantes dentales endoóseos de diferentes diseños o tamaños. Durante el ensayo se simula la carga funcional a la que se encuentra sometido el cuerpo de un implante dental endoóseo y de los componentes de su parte protésica, bajo las peores condiciones. Esta norma recomienda situar el nivel de carga máximo en torno al 80 % del valor de la carga de rotura estática del implante. La carga debe variar sinusoidalmente entre un valor pico y el 10 % de este valor para un coeficiente de asimetría de R = 0,1. El implante dental endoóseo se debe fijar de manera que su eje forme un ángulo de 30° ± 2°con la dirección de aplicación de la carga.
Para fijar el implante durante el ensayo se utilizó un soporte de cobre, el cual debe tener un módulo de elasticidad mayor de 3 GPa.
Determinación de las tensiones equivalentes por el método de los elementos finitos (MEF) aplicando la norma ISO 14801
El método de los elementos finitos permite predecir el comportamiento in vivo mediante la simulación de las tensiones, bajo las solicitaciones de carga que provocaron la fractura, así como la simulación y predicción de la formulación matemática convencional para el estudio de fatiga [9].
En esta sección se describe el procedimiento a seguir para realizar un estudio de elementos finitos mediante el software comercial Ansys Workbench 17.1 (Canonsburg, PA, USA) de un implante dental monocomponente.
Dimensiones específicas del ensayo
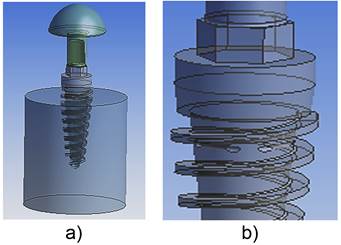
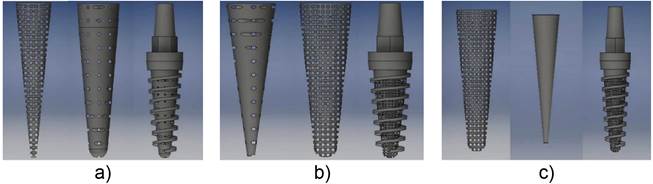
La configuración geométrica de los implantes fue obtenida de una propuesta de diseño previa, figura 1, siendo necesario únicamente la obtención de la geometría del miembro hemisférico y del soporte del implante. Estos tres elementos conforman el ensamblaje requerido para la simulación del ensayo de fatiga, figura 2. Los tres modelos propuestos fueron simplificados para evitar la complejidad en los cálculos. La simplificación se centra en un modelo con la presencia de 2 agujeros pasantes en el cuerpo del implante, figura 2.
 Fuente: Inventor 6
Fuente: Inventor 6Fig. 1 Modelos propuestos: a) Implante más poroso en el núcleo y menos en la superficie, b) Implante menos denso en el núcleo y más poroso en la superficie, c) Implante denso en el núcleo y poroso en la superficie.
Propiedades de los materiales del ensamblaje
En el ensamblaje del miembro hemisférico, implante y soporte cilíndrico se han considerado todos los materiales con comportamiento elásticos, isótropos y homogéneos. Las propiedades de los mismos fueron tomadas de los estudios realizados por Bacchi y Guerola [10, 11], tabla 1.
Mallado
Una vez obtenido el diseño del ensamblaje, éste se transfirió al software de elementos finitos Ansys Workbench 17.1 (Canonsburg, PA, USA).
El mallado del ensamblaje se realizó con elementos tetraédricos de 10 nodos de propósito general, recomendado para geometrías irregulares. La preferencia física seleccionada fue la mecánica, que es la que mejor se adapta a las tensiones y deformaciones. Se fijó una relevancia de 40 para obtener un mayor refinamiento bajo la condición de proximidad y curvatura. Esto permite suavizar las curvas y aumentar el número de celdas alrededor de las aristas.
Condiciones de contorno y cargas
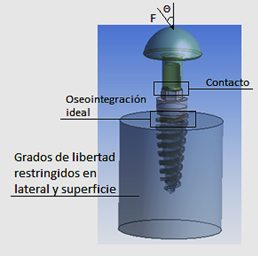
Todos los grados de libertad del cilindro de cobre fueron restringidos, figura 3. Se simularon siete niveles de carga (máximas y mínimas) sobre el miembro hemisférico con ángulo ϴ = 300, garantizando un coeficiente de asimetría R = 0,1, tabla 2.
 Fuente: Ansys Workbench 17.1
Fuente: Ansys Workbench 17.1Fig. 3 Esquema de las condiciones de contorno y la configuración de cargas.
Determinación del comportamiento a la fatiga de los implantes monocomponente utilizando los modelos de la mecánica de la fractura
Cálculo de la vida a fatiga
La falla por fatiga en un componente mecánico tiene lugar en dos etapas. Una fase inicial llamada de iniciación de grieta en la que se generan microgrietas, generalmente en una zona cercana a la superficie o en las proximidades de defectos del material [7, 12] Una fase posterior de propagación de grieta, caracterizada por el crecimiento estable de la misma. Esta fase termina con la fractura total del componente.
La vida de un elemento mecánico que esté sometido a fatiga (NT) puede ser calculada por la suma del período que transcurre hasta que aparece la grieta (Ni) o período de incubación más el tiempo o período necesario para que la grieta se propague hasta la rotura final (Nf), expresión 1.
Determinación de los ciclos de inicio de una grieta de fatiga
El surgimiento de la grieta de fatiga a partir de un determinado defecto (rosca, chavetero, cambio de sección, poro, nódulo, inclusión) puede ocurrir con cargas que no sobrepasan el límite elástico del material, aunque localmente a nivel del grano las tensiones provocan el movimiento de las dislocaciones que dan origen al surgimiento de las grietas [7, 12].
El número de ciclos necesarios para el inicio de una grieta en la interface metal inclusión puede ser determinado por la expresión 2 [14].
Donde, γ es la energía de fractura por unidad interfacial de área, ρ radio del defecto en el eje de mayor magnitud y ΔWd es la energía de deformación en la punta de la grieta.
Cálculo de los ciclos de propagación de una grieta de fatiga
La fase de propagación de una grieta comienza cuando la misma ha alcanzado un tamaño considerable desde el punto de vista macroscópico, de forma tal que su ritmo de crecimiento se estabiliza y no se ve afectado por la microestructura del material y las características de la superficie donde se ha generado. Bajo estas condiciones, el material puede ser considerado continuo y homogéneo, y el crecimiento de la grieta puede ser caracterizado haciendo uso de los conceptos tradicionales de la mecánica de la fractura, ya sea elástica lineal o elasto-plástica [12].
La propagación de la grieta por fatiga constituye la segunda y última etapa en el proceso de rotura. Para determinar su comportamiento es utilizada la expresión (3) de Paris-Erdogan [12, 13], que relaciona la velocidad de propagación de una grieta
Aplicando integral a la expresión 3 se obtiene el número de ciclos hasta la rotura, C0 es el tamaño del núcleo de la grieta inicial y Cf la longitud final de la grieta, expresión 4.
Para el cálculo del factor de intensificación de tensiones se puede utilizar la expresión 5 [13].
Donde a es la longitud de la grieta, Y es un parámetro geométrico,
Procedimiento utilizado para determinar el número de ciclos de fatiga en presencia de defectos
Para el estudio del efecto que genera la presencia de un defecto, se parte del punto de vista desarrollado por Griffith [12, 13], al introducir en el material una discontinuidad o grieta de forma elíptica. En el caso de los agujeros o valle de la rosca, ambos constituyen un defecto. Se admite que la grieta se propagará si la disminución de la energía elástica resultante del aumento de la longitud de esta, es mayor que el incremento de la energía superficial debido al aumento del área de la superficie de la grieta. La energía de deformación Wd se determina utilizando la expresión dada por Petch [12], que para el caso de las tensiones tangenciales queda de la forma siguiente, expresión 6.
Donde, C es la semilongitud del defecto, τ tensión tangencial, G módulo de elasticidad tangencial. El incremento ΔWd en cada ciclo de carga es obtenido sustituyendo las tensiones tangenciales por Δτ = τmáx-τmin y por 2τf que es la resistencia del material al movimiento de las dislocaciones. La expresión anterior quedaría de la forma siguiente, expresión 7.
Iniciación de grietas de fatiga
El inicio de una grieta está acompañado del movimiento de las dislocaciones, por lo que es necesario tener en cuenta que las mismas después que se agrupan son irreversibles. En correspondencia con esto, el número de ciclos debe ser afectado por el coeficiente de irreversibilidad f. Sustituyendo 7 en 2 se obtiene la expresión 8.
En el caso de que el defecto tenga la forma esférica ρ es igual a C, la expresión anterior queda de la forma siguiente.
Propagación de grietas de fatiga
El análisis para la propagación de la grieta se realiza a partir de la expresión 3 de Paris-Erdogan [13], a la cual se le aplica la integral definida, obteniéndose el número de ciclos hasta la rotura Nf, expresión 10.
Para el cálculo del factor de intensificación de tensiones (ΔK) se toma la expresión 5.
El número de ciclos totales se puede determinar sustituyendo la expresión 8 y 10 en 1. Obteniéndose la expresión 11.
Cálculo de la vida útil del implante (NT) y del factor de intensificación de tensiones (∆K)
Utilizando la expresión 11 se puede calcular el ciclo de vida del implante. Los términos de las expresiones son conocidos. Solamente resta adaptarlos a la geometría de los elementos analizados y a las condiciones de carga, las cuales son obtenidas por el análisis de elementos finitos. Siempre se consideró un cuerpo homogéneo y continuo con comportamiento elástico.
Datos requeridos para determinar (NT) y (∆K)
A = 1.8 x 10-14, es un coeficiente que está caracterizado por las propiedades del material e influye linealmente sobre la velocidad de propagación de la grieta [13].
P = 3, es otro coeficiente que depende de las propiedades del material y tiene una influencia exponencial sobre la propagación de la grieta [13].
Y = 1, es un parámetro que depende de la geometría del elemento analizado e influye linealmente sobre el factor de intensificación de tensiones (∆K).
El valor del ∆K se calculó para cada ciclo de carga utilizando la expresión 5 con diferentes longitudes de grieta “a” en la sección transversal crítica del implante. En este caso se propuso para 1, 2, 3, 4 mm.
El comportamiento de la vida útil (NT) del implante con relación a las cargas simuladas se determinó utilizando el valor de la carga máxima (
Resultados y Discusión
Distribución de las tensiones equivalentes Von Mises
Este análisis se realizó en la zona de interés donde ocurre la unión del implante con el casquillo de cobre, según la norma ISO 14801. A continuación se muestran los resultados para diferentes cargas simuladas.
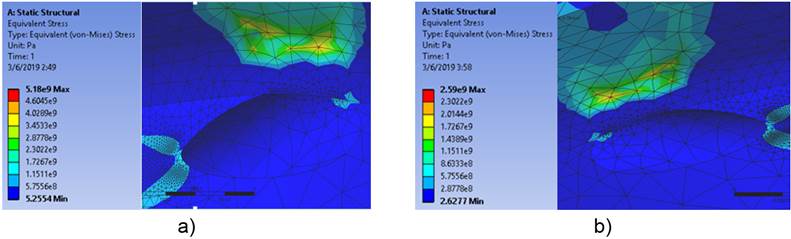
En la figura 4 se puede apreciar que para una carga de 220 N las máximas tensiones equivalentes aparecen en la zona cercana al agujero de manera puntual. El mismo comportamiento ocurre con una carga de 110 N.
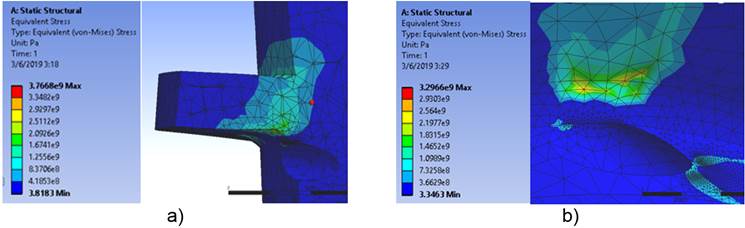
En la figura 5 (a) se evidencia que la concentración de las tensiones aparecen justamente debajo de la unión de la hélice de la rosca con el cuerpo del implante. Constituyendo esta región el punto de partida de una grieta de fatiga [11, 15].
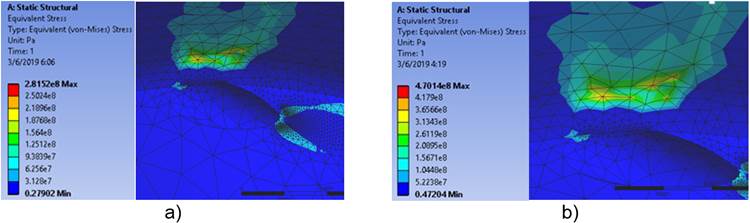
En las figuras de la 5 (b) a la 6(b) la distribución de tensiones está presente en el mismo lugar que para las demás cargas aplicadas. La diferencia radica en la magnitud de los esfuerzos, tabla 3.
Magnitud de las tensiones obtenidas en la modelación por elementos finitos
Los resultados de las tensiones se pueden apreciar en la tabla 3. Estos valores fueron utilizados en las expresiones de predicción de vida, propuestas por la mecánica de la fractura. Las tensiones equivalentes para apertura máxima de grieta que aparecieron durante la simulación entre 220 N y 110 N de carga nominal son de 4604 MPa y 2302 MPa respectivamente, superando el límite de rotura del titanio, el cual es de 737 MPa. Esto es un fenómeno que ocurre puntualmente en la zona del radio de unión entre la hélice y el cuerpo del implante. Igual comportamiento ha sido obtenido por otros autores [10, 14], donde la tensión de apertura máxima de grieta lograda por simulación, alcanzó el valor de 2000 MPa.
Resultados del cálculo del factor de intensificación de tensiones (∆K)
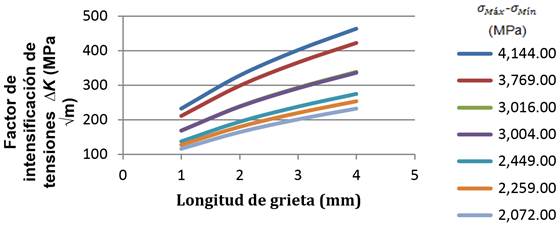
La tabla 4 muestra la evolución del factor de intensificación de tensiones en el vértice de la grieta, conforme esta avanza a través del espesor del cuerpo del implante. Se puede observar el bajo valor que presenta el ∆K cuando la grieta es pequeña.
Tabla 4 Comportamiento del factor de intensificación de tensiones durante el crecimiento de la grieta. Fuente: elaboración propia
| Niveles de tensiones |
Factor de intensificación de tensiones (∆K) para diferentes tamaños de grieta (MPa |
|||
|---|---|---|---|---|
| (MPa) | a = 1mm | a = 2mm | a = 3mm | a = 4mm |
| 2072 | 116,11 | 164,20 | 201,10 | 232,21 |
| 2259 | 126,58 | 179,02 | 219,25 | 253,17 |
| 2449 | 137,23 | 194,07 | 237,69 | 274,46 |
| 3004 | 168,33 | 238,06 | 291,56 | 336,66 |
| 3016 | 169,00 | 239,01 | 292,72 | 338,01 |
| 3769 | 211,20 | 298,68 | 365,81 | 422,40 |
| 4144 | 232,21 | 328,40 | 402,20 | 464,42 |
En la figura 7 se aprecia una tendencia al incremento significativo del factor de intensificación de tensiones con el aumento de las tensiones Von Mises y el tamaño de la grieta.
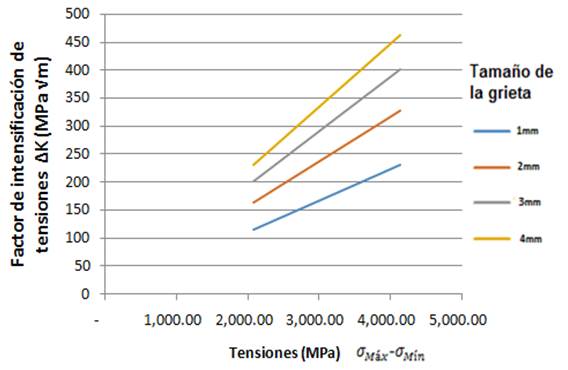
Fig. 7 Comportamiento del factor de intensificación de tensiones para los siete niveles de carga con diferentes tamaños de grieta.
En la figura 8 se muestra el comportamiento del factor de intensificación de tensiones, en función del tamaño de grieta y de las tensiones Von Mises para los siete niveles de carga, evidenciándose un incremento inicial de estos valores y una disminución posterior de los mismos en la medida que aumenta la diferencia entre
Resultados de la vida a fatiga
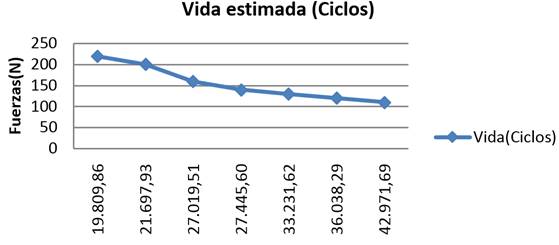
En la tabla 5, la cual muestra la vida estimada en ciclos, se aprecia que la etapa de iniciación de la grieta es mayor que la de propagación. Esta es la fase en la que se generan microgrietas en la zona cercana a la superficie o en las proximidades de defectos del material. Los ciclos iniciales tienden a crecer conforme lo hace la vida estimada para bajas cargas. Para valores altos de la carga, la vida de iniciación es pequeña igual que la vida total.
Tabla 5 Vida estimada del implante (Ciclos). Fuente: elaboración propia
| Niveles de carga (N) |
|
|
|
|---|---|---|---|
| 110 | 39074,42 | 3897,27 | 42971,69 |
| 120 | 35785,12 | 3007,33 | 36038,29 |
| 130 | 32957,15 | 2360,28 | 33231,62 |
| 140 | 27108,93 | 1278,88 | 27445,60 |
| 160 | 26681,50 | 1263,68 | 27019,51 |
| 200 | 21275,53 | 647,62 | 21697,93 |
| 220 | 19322,71 | 487,16 | 19809,86 |
En la figura 19 se aprecia el comportamiento de la vida a fatiga del implante en los siete niveles de carga. Con la aplicación de una carga máxima de 220 N el implante tiene una vida de 1,98x104 ciclos, mientras que al disminuir esta, existe un incremento de los ciclos hasta 4,2
Este comportamiento sugiere hacer nuevas consideraciones en el diseño del implante, sobre todo en aquellos lugares donde la geometría provoca un incremento en la intensificación de las tensiones.
Conclusiones
El uso combinado de ANSYS Workbench 17.1 e Inventor 16 ha permitido, no sólo caracterizar el estado tensional en el sistema de implante, sino que también ha sido posible determinar la evolución del factor de intensificación de tensiones (∆K) durante el desarrollo de una grieta, el cual alcanzó un valor máximo de 464 MPa
De acuerdo a los resultados del número de ciclos iniciales de grieta (1,93 x 104) y de propagación de la misma (4,8 x 102) se evidencia que en el proceso de rotura prevalecerá la etapa de iniciación, la cual depende en gran medida de las propiedades y microestructura del material.
El diseño del implante analizado para las condiciones de simulación a máximas cargas es de 1,98x104 ciclos con relación a lo que exige la norma