Un acercamiento teórico a la modelación del transporte de solutos en el suelo. Primera Parte

A theoretical approach modeling solute transport in soil

 

Dr.C., Prof. Tit.  María T. Alonso González¹, E-mail: [e-mail] ;  Dr.C., Inv. y  Prof. Tit.  Teresa López Seijas² y  Dr.C., Prof. Tit.  María Elena Ruiz³

 

1 Universidad de La Habana, Cuba.

2 Instituto de Investigaciones de Riego y Drenaje, La Habana, Cuba.

3 Universidad Agraria de La Habana, Grupo de Investigaciones Agrofísicas, La Habana, Cuba.

---

 RESUMEN

En la actualidad existen gran variedad de modelos capaces de ayudar en la interpretación de los procesos de transferencia de agua y solutos en la agricultura. En el presente trabajo se exponen enfoques teóricos que fundamentan el transporte de contaminantes en suelos, los cuales son imprescindibles para la comprensión e implementación de herramientas que permitan un acercamiento eficiente a la compleja realidad del sistema agua-suelo-planta-atmósfera. En esta primera parte se tratan las interacciones de los solutos con el perfil del suelo, específicamente el transporte con y sin difusión molecular. Así como, se analiza el modelo matemático del desplazamiento en un volumen representativo elemental y reemplazable, haciendo uso de estudios resumidos por Pfannkuch en 1962, en los cuales relacionaba el valor de D a con el número de Peclet (P e) de difusión molecular. De esta forma se sientan las bases para dar paso a la piedra angular del transporte de contaminantes en medio poroso, la comúnmente conocida Ecuación de Convección-Dispersión.

Palabras clave: contaminación, transporte de agua, convección-dispersión lixiviación.

---

ABSTRACT

At the present time exist great variety of models able to help in the interpretation of the processes of water and solute transport in the agriculture. Presently work theoretical focuses are exposed that base the transport of pollutants in soils, which are indispensable for the understanding and implementation of tools that allow an efficient approach to the complex reality of the system water-plant-soil. In this first part leaves the interactions of the solutes within the profile of soil, specifically the transport with and without molecular diffusion. As well as, the mathematical pattern of the displacement in r epresentative elementary volume , making use of studies summarized by Pfannkuch in 1962. in which it related the value of D a to the Peclet number of molecular diffusion. This way gived the bases to open the angular stone of the solute transport in porous media, the commonly well-known Equation of Convection-Dispersion.

Keywords: contamination, water transport, convection-dispersion, lixiviation.

---

 

 

INTRODUCCIÓN

Es conocido que la fase líquida en el suelo no es agua pura, y que además podemos definir de manera rigurosa el potencial del agua en el suelo considerando la cantidad y diversidad de solutos en la solución del mismo. No obstante, es importante considerar los procesos químicos, físicos y biológicos en el perfil del suelo que distribuyen, diluyen ó concentran la variedad de solutos en la fase líquida del suelo. Considerando que la concentración relativa en la fase líquida es gobernada no sólo por la retención y transporte de agua en el suelo sino también por el manejo de la calidad del agua, así como el movimiento a través de las raíces de las plantas, es que puede considerarse el comportamiento de solutos en el suelo a través de los macro y microporos (Kutilek and Nielsen, 1994).

En estudios primarios Slichter (1905) explicó que el hilo central del agua en cada poro capilar del suelo se mueve más rápido que el agua a través de las paredes de los poros. Treinta años después Kitagawa (1934) estudiando la dispersión del cloruro de sodio desde un punto fuente en un suelo arenoso saturado expresó el proceso mixto como una función de la media de la velocidad del agua a través de los poros. Aproximadamente 20 años después, Bosworth (1948) y Taylor (1953) examinaron las contribuciones de la difusión molecular en un tubo capilar cilíndrico. Durante los siguientes cuarenta años las investigaciones se aceleraron debido al crecimiento de la importancia de la calidad del agua (Kutilek, and Nielsen, 1994).

Arnolds (2006) señala que la Ciencia del Suelo, tiene retos grandes que afrontar: resolver problemas que le permiten realizar una interacción dinámica entre esta ciencia y las nuevas fronteras entre las que se encuentran la Microbiología y Bioquímica enfatizando al tema de la biodiversidad, las interacciones suelo-planta y el paso de químicos a través del suelo y del ecosistema en general. Otros aspectos relacionados con la salud humana y la conservación de agua y suelos, están demandando cada día mayor atención en la mayoría de los países del mundo. Es decir, se requiere una aproximación más integrada.

Teniendo en cuenta que el movimiento de solutos a través del suelo es gobernado por dos tipos de procesos conceptualmente diferentes: el transporte en la fase de agua y las interacciones con las otras fases en la frontera de esta, y que en general, ambos son procesos complejos no-lineales; constituye entonces un reto realizar una adecuada descripción de los mismos, especialmente en sistemas como los suelos naturales (Roth and Jury, 1993).

La heterogeneidad del medio poroso es un problema que incide en diferentes aplicaciones o estudios del campo agrícola e incluso fuera del mismo como es el caso de la Ingeniería de Petróleos. En particular para la Física de Suelos la predicción del movimiento del agua y los solutos se hace más compleja en la medida en que la modelación del sistema agua-solutos-suelo-planta sea más cercana a la realidad, es por ello que para lograr establecer elementos de análisis, en general, es preciso simplificar al máximo el modelo del sistema físico y describir sus interacciones y parámetros de la manera más simple posible.

Este ensayo pretende abordar en una primera parte las bases teóricas del transporte de solutos en los suelos agrícolas, enfatizando en los modelos matemáticos que han sido abordados por diferentes autores y su evolución a lo largo de más de 60 años, precisando aquellos parámetros e interacciones más importantes para una mejor comprensión de los modelos de simulación más utilizados en los últimos años en aplicaciones agrícolas y medioambientales.

Consideraciones teóricas en la modelación del transporte de solutos en los suelos agrícolas

Interacciones de Solutos. Se consideran las interacciones físicas de solutos que juegan un papel primario en la distribución de solutos en el perfil del suelo.

•  Difusión Molecular

La energía térmica proporciona, un movimiento continuo y constante de la fase líquida y gaseosa de un sistema de suelo. Fick (1855) proporcionó una base teórica para este movimiento mostrando que la difusión molecular obedece a la misma ley matemática que Newton obtuvo para la velocidad de flujo y Fourier para el flujo de calor según la primera Ley de Fick de difusión de estado, ya sea gaseoso o de solutos , estos se mueven o difunden relativo a una mezcla ó solución en la dirección en que decrece la concentración de estas especies justo como el flujo de calor por conducción en la dirección del decrecimiento de temperatura. (Kutilek and Nielsen, 1994). Para estas condiciones se cumple:

(1)

donde:

q -flujo difundido [M·T^-1], A–área de la sección transversal [L²], C -la concentración [M L^-3], x – coordenada espacial, D - coeficiente molecular
[L²·T^-1].

La compleja geometría de un suelo con relación al paso de la difusión y al área de la sección transversal es usualmente descrita en términos de dos parámetros: la tortuosidad y la porosidad. Si se asume que las condiciones isotérmicas prevalecen, el volumen de un suelo que queda es constante, los sólidos del suelo son inertes, y por conveniencia, se considera la difusión gaseosa en una dimensión en un suelo completamente seco. Bajo condiciones de estabilidad con C(0) = C₁ y C(L) = C₂ , el flujo de difusión para un poro cilíndrico de longitud L e , se convierte en:

(2)

donde: D 0-coeficiente de difusión gaseosa, A_e-APL/L_e-área de la sección transversal de un poro cilíndrico. P -porosidad .A-área de la sección transversal de suelo.

Igualando (2) con un modelo para longitud L se obtiene:

(3)

Esta es la forma sugerida por Buckingham (1904), donde el término (L/L_e) es llamado tortuosidad e igual a cos²a. En el trabajo de Penman (1940) es usado comúnmente el valor de (L/L_e )² = 0.66 y el ángulo de 0,61 ó 35 0 entre el poro y la partícula sólida del suelo.

Ecuaciones similares a (3) son fácilmente derivadas para los coeficientes de difusión en un suelo parcialmente saturado de agua así como para la difusión de solutos en suelos saturados y no saturados. Por ejemplo: Sallam et al. (1984), experimentalmente mostraron que el producto P·(L/L_e)² en la ecuación (4) para la difusión gaseosa en suelos no saturados es más cercano a a^{3.10 P-2} que a a^{10/3 P-2} (Millington y Quirk, 1959), dónde a– es la porosidad ocupada por aire. Incluso para condiciones isotérmicas, y adicionando el gradiente de concentración, se tiene para simplificar más la discusión, la omisión del gradiente de presión y las fuerzas externas que actúan de forma desigual en los gases y tipos de solutos. Se debe recordar que el valor del coeficiente de difusión depende de la naturaleza de los gases que se oponen a la difusión ó del tipo de solutos (Kutiklek and Nielsen, 1994).

•  Desplazamiento sin difusión molecular

De la definición de viscosidad, la fuerza por unidad de área, t , requiere ser expresada como un flujo de viscosidad, h,

(4)

donde:

v –es la velocidad del flujo y r–la coordenada normal a la fuerza.

Teniendo en cuenta la distribución de velocidad dentro de un tubo capilar horizontal de radio a durante un flujo continuo e integrando se tiene la conocida distribución de velocidad parabólica:

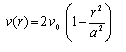(5)

donde:

v(0=2v₀. La razón de flujo volumétrico Q (cm³·s^-1) a través de los capilares es fácil de obtener integrando v(r) con el área de la sección transversal del capilar.

(6)

 

Si asumimos que no hay difusión molecular y que solo depende de la velocidad del fluido, cuál será la distribución de un segundo flujo de concentración C₀ como desplazamiento de un flujo de concentración inicial cero en un capilar? Considere que la solución C₀ entra en el tubo, desde x=0 en un tiempo t=0. La concentración C promediada sobre el corte de la sección del capilar a una distancia x es:

(7)

 

FIGURA 1. Distribuciones parabólicas de una solución C0 invadiendo un capilar (a) que da lugar a una distribución media de la concentración a lo largo del tubo (b).

En esta figura, el paraboloide del flujo desplazado C₀ en un capilar da lugar a una distribución lineal de la concentración. Cuando el frente invadido de C₀ a alcanzado la distancia de 2L, la concentración media a través del plano normal a una distancia del capilar de es C₀/2 .De manera interesante, la concentración media en el flujo que se mueve a través del plano L desde el instante no es C₀/2 y sí 3 C₀/4. La concentración media del flujo para x=L es:

(8)

donde r^t=a(1-L/2v₀t)^1/2 es la 1/2 frontera radial entre el flujo desplazado (C=C₀ para r< r´) y el flujo original (C=0 para r> r´). Ver ecuaciones siguientes:

Integrando (8) conlleva a:

Donde: p=v₀ t/L es la proporción entre el volumen del flujo que pasa por x=L y el volumen del capilar entre 0=x=L. El volumen de poros del efluente ó simplemente volumen del poro es conocido comúnmente como p. El valor de C=3 C₀/4 para p=1 y aproximado a la unidad para p® ¥.Ver Figura 2.

 

FIGURA 2. a-Diagrama del corte transversal del volumen elemental del flujo que se mueve en un capilar. b- Concentración media relativa al flujo saliente del capilar de longitud L como función del volumen poral del efluente.

 

•  Desplazamiento con difusión molecular

Taylor (1953) proporcionó enfoques para separar la dispersión de solutos en un capilar, causado por la difusión molecular de este en la distribución de velocidad de un fluido. Asumiendo que la concentración de soluto en un capilar es simétrica al eje central y la velocidad del flujo es descrita por (5), la mezcla de un soluto por difusión y convección es descrita por:

(9)

Donde se asume que el coeficiente de difusión molecular D m es independiente de la concentración.

Las siguientes condiciones iníciales y de fronteras aproximan la suposición de que la solución desplazada C₀ que entra en un capilar con velocidad uniforme desde x=0 comenzando en t=0:

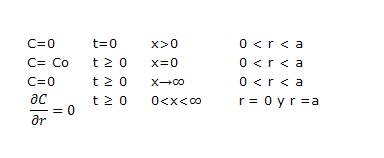(10)

Detalles sobre la solución numérica de (9) sujeta a (10) son dados por Amanthakrishnan y otros (1965). El caso límite para pequeñas velocidades de flujo, cuando v®0, la solución analítica es:

,

encontró que la densidad del flujo del soluto de x₁ es:

(11)

Aris (1956) extendió el análisis anterior para capilares irregularmente formados que también incluye la contribución mixta de la difusión molecular longitudinal. Su análisis permite una distribución de velocidad local no parabólica en capilares irregulares y una concentración dependiente del coeficiente de difusión molecular, lo que está dado por el coeficiente de difusión aparente:

(12)

donde:

a-es un número adimensional que depende del corte de la sección, ã es el radio efectivo y u_o-la velocidad media del flujo.

  Desplazamiento en un volumen representativo elemental y reemplazable en medio poroso

La difusión molecular, la convección de solutos y el flujo de agua en poros individuales son descritos a escala poral mientras que la difusión ó dispersión de solutos en agua ocurre a escala macroscópica. Bear y Bachmat imaginaron el medio poroso como una red de canales estrechos aleatoriamente interconectados de varias longitudes, cortes seccionales y orientaciones. El líquido químicamente inerte y no compresible de viscosidad variable y densidad que satura los poros obedece a la Ley de Poiseulle y tiene dos componentes, uno solvente y otro soluto. Después de derivar y promediar la ecuación de conservación y movimiento de masa para un líquido en y a través de los canales, estas ecuaciones locales fueron promediadas para obtener las ecuaciones macroscópicas. Se repite aquí la ecuación final de conservación de masa en una dirección evitando la notación tensorial de segundo orden necesario para el análisis tridimensional (Kutilek and Nielsen, 1994):

Donde u y C- son los valores promedios en un REV (Volumen Elemental Representativo) y D_c y D_m -son los coeficientes de la dispersión convectivo (ó mecanicista) y de difusión molecular respectivamente. Combinando los últimos coeficientes en un único término D_a (comúnmente llamado coeficiente de dispersión hidrodinámica ó coeficiente de difusión aparente), tenemos que:

(13)

Para la cual varios investigadores han buscado las relaciones teóricas y experimentales entre el valor D_a (que abarca la mezcla de solutos en las dos escalas: escala poral y secuencial en un REV) y el valor u (promedio de la velocidad del agua que pasa por los poros usualmente estimada por la razón de la densidad del flujo darciano y el contenido de humedad q).

El resultado de varios estudios resumidos por Pfannkuch (1962) relacionan el valor de D a con el número de Peclet de difusión molecular P_e- igual a ud/D_m , donde d–tamaño medio de la partícula sólida u otras características de longitud del medio pososo. Reconociendo que los efectos de ambas: difusión molecular y convección en la mezcla de solutos en experimentos típicos de una sola dimensión son difíciles de separar; Fried y Combarnous (1971) sugirieron cinco rangos de los números de Peclet ó zonas para delinear las relativas magnitudes en cada proceso. Para el laboratorio ó campo, se sugiere que las siguientes cuatro zonas serán suficientes excepto bajo algunas condiciones de campo cuando el flujo turbulento debajo de las grandes hendiduras y grietas prevalecen durante períodos de rápida infiltración:

Zona 1 Pe<0.3 Da=Dm Dc<<Dm

Zona2 0.3<Pe<5 Da=(Dm+Dc) Dc»Dm

Zona3 5< Pe<20 Dc<Da<(Dc+Dm) Dc>Dm

Zona4 Pe<20 Da=Dc Dc>>Dm

Las Zonas 1 y 2 son ilustradas en la Figura 3 para un experimento de desplazamiento miscible conectado con una columna uniformemente cubierta con 390 µ inicialmente saturada con 0,10 de N NaCl.

 

FIGURA 3. Curvas de ruptura del 36Cl para un desplazamiento de 0.10 N NaCL en dos cantidades de flujo a través de una columna uniforme.

Esta solución inicial fue desplazada con dos diferentes velocidades de agua en poros (0.499 y 7.80 cmh^-1)con una solución de igual composición química, conteniendo Na 36 Cl para observar el proceso donde se mezclan y se igualan la distribución de concentración medida en x=30 cm con una solución de (13) sujeto a las siguientes condiciones (Kutilek and Nielsen, 1994):

C=0 x>0 t=0

C=C o x =0 t>0 (14)

C=0 x®¥ t = 0

Donde C_o es la concentración de ³⁶CL. Para cada una de las dos velocidades de agua en los poros, la Figura 4, muestra los valores medidos de la concentración relativa C/C₀ y la suavidad de las curvas que satisfacen (13) y (14) ajustados a los datos por una selección de la única entidad no medible Da. Los valores de Da para cada valor de u satisfacen la ecuación (Fried and Combarnous, 1971):

(15)

donde:

Dm =1,98·10^-5 cm²·s^-1 (Wang, 1952) y d=3,9·10^-2 cm. Experimentalmente se determinaron los valores de a=0,51 y n=1,02 de acuerdo con los sugerido por Fried y Combarnous (1971). Para bajas velocidades de agua en los poros (0,499 cm·h -1 ) con Pe=0,27 (correspondiente al extremo superior de la zona1), 83% de la mezcla es causado por la difusión molecular. Para velocidades mayores (7,80 cm·h^-1) con P_e=0,43 (correspondiente al extremo inferior de la Zona2), solo el 23% de la mezcla es causada por la difusión molecular.

La ecuación (15) frecuentemente es reducida a:

Da=0,67 Dm+ß· n (16)

Para las Zonas 3 y 4 se desprecia el término de la difusión molecular y se toma el valor de n=1. En tales instancias ß es llamado dispersividad.

Piedra angular de la descripción teórica del transporte de solutos en medio poroso.

Para la presentación de la piedra angular de la descripción teórica del transporte de solutos en medio poroso, se reconoce que su forma es provisional en varios aspectos, además de estar llena de incertidumbres en la aplicación a escala temporal (Skopp, 1986)y espacial (Dagan, 1986), las cuales no son fáciles de resolver.

En este punto se deben abordar conceptos actuales importantes como la concentración residente y concentración en el flujo y pueden plantearse las siguientes interrogantes:

•  ¿Cuando se podría estar interesado en una concentración en el flujo y qué relación habrá entre las mismas?

•  ¿Qué relación existirá entre el flujo del agua y el transporte de contaminantes?

Estas y otras respuestas importantes complementaran los fundamentos teóricos en el transporte de solutos en suelos que se expondrán en la segunda parte de este trabajo.

  CONSIDERACIONES PARCIALES

•  Existe una relativa importancia de la difusión molecular comparada con la convección, debido a esto es posible completar las reacciones químicas y de intercambio que tienen lugar en la estructura microscópica del suelo.

•  Bajo condiciones de saturación, la cantidad relativa de solutos que está siendo desplazado depende de la concentración de solutos en agua, cuando la velocidad media en los poros es mayor comparada con el transporte por difusión molecular.

•  Si asumimos que no hay difusión molecular la velocidad del flujo puede estimarse por (5) por lo que la distribución de un flujo de concentración C 0 con concentración inicial cero en un capilar estará expresada por la concentración promedio resumida en la tabla de este epígrafe. Además, aún para geometrías muy simples como un tubo capilar, no resulta sencillo conciliar con la forma de la curva de la distribución de concentración en un tubo vista en la Figura 1.b.

•  Si se asume la difusión molecular, la densidad del flujo dado por (11) muestra que un soluto es dispersado relativo al plano en que se mueve con una velocidad v₀ , exactamente como si estuviera mezclado por la difusión molecular (comparándolo con (1) ), pero con un coeficiente aparente de difusión D_a definido por: D_a=a²/48D_m

•  Varios investigadores usan (11) u otros tipos de difusión molecular como: ∂C/∂t=D·∂² C/∂x² con suposiciones particulares considerando el papel de la difusión molecular longitudinal y transversal de una relación teórica ó experimental de Da como una función de u ( (13) ó (14) ). Simpson (1969), en un artículo referativo sobre la relación entre la velocidad del agua en los poros y el valor del coeficiente longitudinal de dispersión expone “Los experimentos críticos restantes pueden llevarse a cabo con una investigación sistemática del efecto en la dispersión de los cambios en la difusividad molecular”. Años más tardes Expósito y otros (1979) presentaron una revisión crítica de diferentes teorías utilizadas para describir el transporte de solutos en medio poroso. Sus comentarios relacionados con los enfoques de las bases teóricas sobre mecánica de fluidos y cinemática empleando varias técnicas estadísticas muestran las mejores oportunidades para perfeccionar la comprensión del desplazamiento miscible en un medio poroso reemplazable.

 

REFERENCIAS BIBLIOGRÁFICAS

1. AMANTHAKRISHNAN, V, W.; N. GILL and A.J.BARDUHHN: Laminar dispersion in capillaries: Part I, Mathematical Analysis, Am. Inst. Chem. Eng. J., 11:1063-1072, 1965.

2. ARIS, R.: On the dispersion of solute in a fluid flowing through a tube, London A Proc. Roy. Soc. 235: 67-77, 1956.

3. ARNOLDS, OLAFUR: The future of soil science, edited by Alfred E. Hartemink (1964). Wageningen: IUSS International Union of Soil Sciences. ISBN 90-71556-16-6, Agricultural University of Iceland , Faculty of Environmental Sciences, Keldnaholt, 112, Reykjavik, Iceland, E-mail: [e-mail] 2006.

4. BEAR, J. and BACHMAT: A generalized theory of hydrodynamic dispersion in porous media. Proc. Intl. Assoc. Sci. Hydrol. Symp. Haifa, Publ. No. 72, 1967.

5. BOSWORTH, R.C.L.: Distribution of reaction times for laminar flow in cylindrical reactors. Phil. Mag. 39: 847-862, 1948.

6. DAGAN, G.: Statistical theory of groundwater flow and transport: Pore t6o laboratory, laboratory to formation and formation to regional scale. Water Resource, Res., 22: 103-135, 1986.

7. EXPOSITO, G., V.J. GUPTA and R.N. BHATATTACHARYA: Foundation theories os solute transport in porous media: a critical review, Advances in Water Res., 2: 59-68, 1979.

8. FICK, A.: "Uber Diffusion", Leipzig, Ann, Der ohys, 94:59-86, 1855.

9. FRIED, J.J. and M.A. COMBARNOUS: Dispersion in porous media, Advances Hydrosci., 7: 169-282, 1971.

10. KITAWA, K.: «Sur le dispersement et l´écart moyen de l´écoulement des eaux sonterraines», Kyoto Imp. University, Mem. Coll. Sci., Series A, 17: 37-42 and 431-441, 1934.

11. KUTILEK and NIELSEN: Soil Hydrology, 274-279, Textbook for the students of soil science, Cremlingen-Destedt: Catena-Verl, 1994.

12. MILLINGTON , R.J. and QUIRK: Permeability of porous media, Nature, 183: 387-388. 1959.

13. PENMAN, H.L: “Gas and vapor movements in the soil: The diffusion of vapors through porous solid. II. The diffusion of carbon dioxide through porous solids”, J. Agr. Sci., 30: 436-462 and 570-581, 1940.

14. PFANNFUCH, H.O. «Contribution a l´étude des dleplacements de fluids mscibles dans un milieu poreux», Revue de l´Intitut Frnacais du Petrole 18: 215-270, 1962.

15. ROTH, K. and W.A. JURY: Modeling the transport of solutes to groundwater using transfer functions, J. Environ. Qual., 22: 87-493, 1993.

16. SALLAM, A., W.A. JURY and J. LETEY: Measurement osf gas diffusion coefficient under relatively low air filled porosity, Soil Sci. Soc Am. J., 48: 3-6, 1984.

17. SIMPSON, E.S.: Velocity and the losngitudinal dispersion coefficient in flow through porous media, pp.201-214, In: R.J.M. De Wiest ( Ed): Flow through porous media, Acadenic Press , New York and London , 1969.

18. SKOPP, J. Analysis of time dependent chemical processes in soils, J. Environ Qua., 15: 205-213, 1986.

19. SLICHTER, C. S.: Field measurements of the rate of movement of underground waters. Water Supply and Irrigation, pp. 9-122, paper No. 140, series O, U.S. Dept Interior, U.S. Geol. Survey, 1905.

20. TAYLOR, G.I.: Dispersion of soluble matter in solvent flowing slowly through a tube, London A., Proc. Roy. Soc., 219: 186-203. 1953.

 

Recibido 20/12/09, aprobado 12/09/10 , trabajo 37/10, puntos de vista.