Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr v.19 n.4 San José de las Lajas oct.-dic. 2010
Análisis de neumático por elementos finitos con vistas a la determinación de coeficientes de cargas dinámicas en estructuras de máquinas agrícolas
Analysis the tires for finite element to determination coefficient of dynamics loads in structures of agricultural machines
Ing., Adiestrado Raudel Flores Moreno1, E-mail: raudelfm@isch.edu.cu ; Dr.Cs., Inv. Tit. Arturo Martínez Rodríguez1; Estudiante Gelasio Valerio Pacheco Sánchez2; Estudiante Vladimir Lenin Reyes de la Cruz2; e Ing. Egresado Alberto Iraldo Dávila García1.
1 Universidad Agraria de La Habana (UNAH), Centro de Mecanización Agropecuaria, Apto. Postal: 18-19, San José de las Lajas, La Habana, Cuba, CP:32 700.
2 Universidad Autónoma Chapingo, Departamento de Ingeniería Mecánica Agrícola (DIMA), México.
RESUMEN
La determinación incorrecta de los coeficientes de cargas dinámicas, traen aparejadas otras dificultades relacionadas con el sobredimensionado de las piezas, lo cual da lugar a exceso de peso y gastos adicionales. En las máquinas agrícolas es de vital importancia el estudio de los sistemas de amortiguación, ya que estos son capaces de absorber las cargas de impacto disminuyendo de esta forma las afectaciones que estas provocan en las estructuras. En el presente trabajo se abordan métodos de cálculo mediante modelación con herramientas de diseño asistido por computadora y análisis por elementos finitos con vistas a calcular los coeficientes de cargas dinámicas ante la presencia de elementos de amortiguación tales como los neumáticos típicos de máquinas agrícolas. Una evaluación del modelo, empleando el análisis por elementos finitos combinado con métodos de cálculo tradicionales de coeficientes de cargas dinámicas, durante un impacto provocado sobre un puente trasero de carreta agrícola apoyado sobre neumáticos, sometido a una caída brusca desde una altura de 5cm, arrojó una disminución del 17,54% de las tensiones en los puntos más peligrosos de dicha estructura, producto de la acción amortiguadora de los neumáticos.
Palabras clave: impacto, elementos finitos.
ABSTRACT
The incorrect determination of the dynamic load coefficient, are joint to other difficulties related to the over dimensioned of the parts, which produce and excess of weight and additional expense. In the agricultural machines is of great importance the study of the shock systems, due to the fact that they are able to absorb the impact load decreasing in this way the affectations that produce on the structures. In the present Work approach mainly methods of calculation by means of Assisted Design by Computer and finite element analysis for determination dynamic load coefficient with presence of shock elements how the typical tires of agricultural machine. An evaluation of the model, use finite element analysis combines with traditional calculation methods of dynamic load coefficient, during an impact cause in back beam of agricultural trailer leaning on tires, subjected to an abrupt fall of a height of 5 cm, throw a decrease of 17,54% in the tensions in the danger point of the structure, product of sock action of the tires.
Keywords: impact, finite element.
INTRODUCCIÓN
Las exigentes condiciones de los terrenos y características pesadas de los suelos, hacen habitual en la agricultura cubana los ejemplos de máquinas e implementos, tanto de fabricación nacional como de importación, que sufren deformaciones en su estructura o roturas frecuentes en sus órganos de trabajo.
La determinación de coeficientes de cargas dinámicas que posibiliten obtener, con un grado de exactitud aceptable, los estados tensiónales y deformacionales en piezas y estructuras sometidas a cargas de impacto, presenta un alto nivel de dificultad, sobre todo cuando los elementos sometidos a la acción de dichas cargas presentan una configuración que no sea simple, siendo necesario implementar otros métodos que simplifiquen el cálculo y permitan abordar casos no contemplados como típicos.
En el caso de acciones dinámicas de impacto los métodos menos rigurosos de determinación de coeficientes de cargas dinámicas, contemplan el cálculo de la energía potencial gravitatoria o de energía cinética del cuerpo que impacta, así como la energía de deformación del cuerpo impactado (Burr, 1995; Pisarenko, 1989).
Sin embargo, otros métodos más rigurosos, consideran además la energía cinética del cuerpo impactado, y tiene en cuenta el efecto de la masa de dicho cuerpo, lo cual ha sido demostrado que incide en los resultados finales del cálculo, excepto cuando la masa del elemento impactado es muy inferior a la del elemento que impacta (Martínez et al., 2009).
Por lo general este tipo de determinación implica operaciones complejas, tales como hallar la ecuación de la curva elástica de la pieza o estructura y determinar la velocidad a partir de la derivada con respecto al tiempo de la deformación (Roark y Young, 1989). Este tipo de cálculo ha sido realizado para casos típicos (los más sencillos) de vigas sometidas a determinados tipos de solicitaciones, ofreciéndose en manuales y libros los factores de corrección que permiten determinar, para estos casos tipos, los coeficientes de cargas dinámicas. Sin embargo, en los casos con algún grado de complejidad, o que sencillamente se diferencien de los casos típicos, se incrementa notablemente el nivel de dificultad en los cálculos analíticos.
En lo relacionado con la consideración y cálculo de coeficientes de cargas dinámicas durante el cálculo de elementos de máquinas agrícolas, solo se reporta en Cuba una investigación realizada por Goitizolo (2007), en la que aplica el método tradicional de Pisarenko (1989), durante el cálculo de un puente delantero de tractor al que se le incrementa la capacidad de paso.
Modernamente, el método de los elementos finitos ha venido empleándose con éxito no solo en el análisis de estructuras si no que también se han realizado estudios en neumáticos como importantes elementos amortiguadores, debido a que en la mayoría de los casos son los primeros en recibir los impactos, esto se debe a que todo el tiempo se encuentran en contacto con la superficie del suelo y en el caso particular de la maquinaria agrícola deben transitar por terrenos irregulares con la existencia de obstáculos físicos que inciden directamente sobre ellos.
Los primeros trabajos de aplicación del MEF donde se tienen en cuenta los neumáticos, se realizaron en el estudio de interacción neumático-suelo que se hicieron a finales de la década del 60 y principios del 70, estos fueron publicados por Perumpral (1969), Perumpral et al. (1971), Coleman y Perumpral (1974), Yong y Fattah (1976), Yong et al. (1978). Pero es importante destacar que en estos estudios no se representa la interacción neumático-suelo sólo se simula el efecto de una presión uniforme, distribuida sobre un área de contacto circular aplicada a una superficie rígida o deformable o en algunos casos como la acción de una rueda rígida.
Varios investigadores consideran que la más exacta aproximación del desempeño de un neumático fue hecha en el Instituto de Investigaciones del Automóvil, en la Universidad de las Fuerzas Armadas de Alemania, en Hamburgo, por Aubel (1994), con fines de estudios de traficabilidad. En este modelo se representa por separado el neumático y el suelo, los cuales interactúan durante la simulación. Sin embargo, el neumático es desarrollado por una banda más o menos elástica alrededor de una llanta, el efecto del neumático lleno de aire no se representa. Este modelo fue mejorado por Fervers (1999), llevando a una representación plana todas las partes componentes del neumático, simulando además, el efecto de la presión de inflado y la transmisión de fuerzas por la carcaza, entre la llanta y la banda de rodadura (Schmid, 1995; Shoop, 2001).
El comportamiento mecánico de los neumáticos ha sido modelado en computadora por diversos autores. Nackenhorst y Ziefle (2005), usan procedimientos numéricos que consideran los problemas de contacto entre los elementos, incluyendo materiales provistos de elasticidad. Bolarinwa y Olatunbosun (2004), realizan la modelación de un neumático mediante elementos finitos, lo que les permite modelar el efecto de explosión del neumático cuando es inflado a presiones más allá de la máxima recomendada por el fabricante. Para el análisis emplean un modelo procesado mediante el programa ABACUS.
Kazuyuki Kabe y Masataka Koishi (2000), aplicaron el método por elementos finitos para el estudio de neumáticos, la mayoría de estos análisis fueron realizados de forma estática, debido a que los neumáticos constituyen una estructura demasiado complejo para su modelación debido a la cantidad de elementos que posee en su interior.
El presente trabajo está dirigido a determinar, a partir de métodos basados en el empleo de herramientas de diseño asistido por computadora, en particular el método de los elementos finitos, el efecto de un neumático agrícola como elemento amortiguador en estructuras de máquinas agrícolas sometidas a cargas de impacto.
MATERIALES Y MÉTODOS
Determinación de los coeficientes de cargas dinámicas del neumático
En un estudio realizado por Martínez et al. (2009), se abordó la comparación de los resultados de los cálculos efectuados por los dos métodos tradicionales de calculo de coeficientes de cargas dinámicas, de manera de poder valorar el error que implica la no consideración de la masa del cuerpo impactado en la exactitud de los cálculos y poder determinar si existe diferencia o no en el empleo de un método con respecto a otro.
Según dicho estudio se aprecia que para valores de la masa inferiores en el orden de la masa del objeto que impacta, o menor, la diferencia entre los coeficientes de cargas dinámicas calculados por ambos métodos no es significativa y que esa diferencia aumenta cuando se incrementa la masa del cuerpo impactado, resultando hasta un 60% mayor el coeficiente calculado por el método simplificado cuando la masa del elemento golpeado es 10 veces superior a la del cuerpo que impacta.
Para este estudio en la Tabla 1 se muestra los datos empleados para la evaluación de las expresiones para kd y KD.
TABLA 1. Datos empleados para la evaluación de las expresiones para kd y KD.
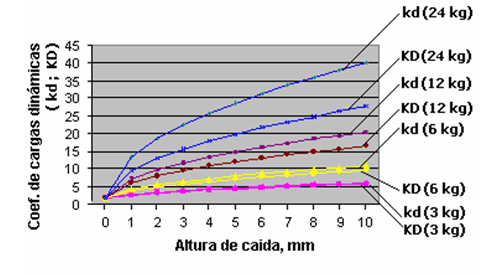
En la Figura 1 se muestra los resultados de los cálculos evaluado por los dos métodos para kd y KD respectivamente. De la figura se aprecia que en todos los casos evaluados, el valor obtenido para el coeficiente de cargas dinámicas kd, que no considera la masa del cuerpo impactado, es superior al coeficiente KD que tiene en consideración esta masa. Asimismo se aprecia que la diferencia entre los coeficientes de cargas dinámicas calculados por ambos métodos, no es significativa cuando la masa de la viga impactada es del orden o menor que la masa del objeto que impacta, y que esta diferencia se incrementa a medida que aumenta la masa del cuerpo impactado.
FUGURA 1. Coeficientes de Cargas Dinámicas (kd y KD) en función de la altura de caída de la carga que impacta y de la masa del elemento impactado.
En la Tabla 2 se muestra los datos de las masas del cuerpos impactado (neumático 7.50-20-6), y la del cuerpo que impacta (remolque agrícola).
TABLA 2. Masa de los objetos de estudio
Analizando estos datos, puede determinarse que el neumático agrícola, que se considera el objeto impactado con respecto al cuerpo que impacta (remolque agrícola), poseen una relación masa impactada/masa que impacta de 1/9, siendo factible aplicar el método más sencillo para la determinación de los coeficientes de cargas dinámicas (kd), que no tiene en cuenta la masa del cuerpo impactado. En este caso el más sencillo, se parte del planteamiento de que la energía potencial del cuerpo que impacta (m . g . H) se convierte en energía potencial elástica que acumula el cuerpo impactado durante la deformación.
Según la teoría clásica las tensiones dinámicas máximas (sdmáx) durante la flexión provocada por el impacto se determinan por medio de la expresión:
donde:
sest- tensión estática;
kd- coeficiente de cargas dinámicas (Pisarenko, 1989).
El método tradicional más sencillo está dado por la expresión:
donde:
dest-es la flecha máxima de la viga (cuerpo impactado) bajo la carga estática (m.g).
El cálculo de las tensiones y deformaciones estáticas en el elemento de amortiguación objeto de estudio, requeridos para la determinación de los coeficientes de cargas dinámicas, se efectuó a partir de la modelación digitalizada de dichos elementos empleando herramientas de diseño asistido por computadora (CAD).
Para la determinación del coeficiente de cargas dinámicas, el valor obtenido de deformación máxima (flecha estática) mediante el análisis por elementos finitos se sustituye en la expresión de Pisarenko, (1989), señalada con el número 2, para cuya evaluación se elaboró un software en soporte Mathcad 2000 Professional. Este software posibilita variar los valores de los diferentes datos de entrada, ofreciendo los resultados, tanto en forma tabulada, como gráfica.
RESULTADOS Y DISCUSIÓN
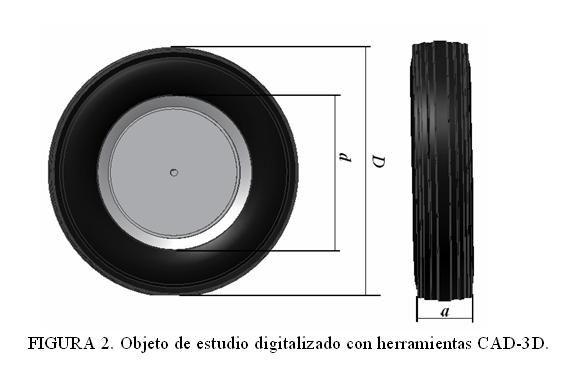
Se obtuvo como resultado un modelo del neumático de máquinas agrícolas (7.50-20-6), que posee un diámetro exterior D, un diámetro interior d y con un ancho a, como se muestra en las Figura 2.
La presión de inflado determina la carga que puede soportar el neumático de maquinas agrícolas (7.50-20-6), según los datos que se muestran en la Tabla 2 del catalogo de la empresa de fabricación de neumáticos Poligom de San José de las Lajas, se pude determinar que este neumático con su máxima presión de inflado (3,10 kg/cm2) es capas de soportar cargas cercanas a los 1 000 kg.
En la Tabla 3 se muestran los parámetros de entrada empleados para la corrida del programa de análisis por elementos finitos y en la Tabla 4 las características de la malla utilizada durante la aplicación estática de la carga en los elementos de amortiguación objetos de estudio.
TABLA 2. Presión de acuerdo con la carga aplicada
TABLA 3. Parámetros de entrada empleados para el análisis por elementos finitos durante la aplicación estática de la carga
TABLA 4. Característica de la malla
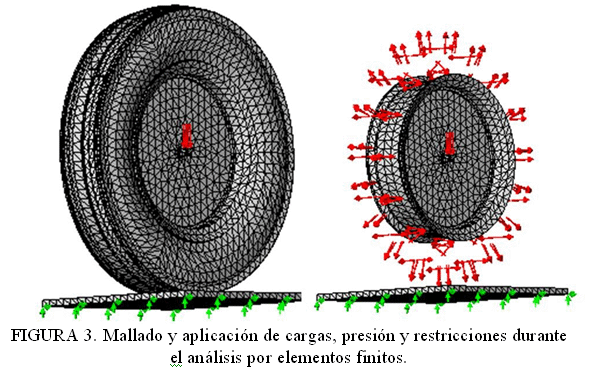
En la Figura 3 se muestra el mallado realizado para el análisis, así como los lugares de aplicación de las cargas y la presión en el interior del neumático (color rojo), y las restricciones (color verde). Los contactos entre los elementos fueron soldado, de manera de poder observar la deformación. El nivel de carga aplicado fue de 10 000 N correspondiente con la capacidad de presión de aire suministrado al neumático (3, 10 kg/cm2).
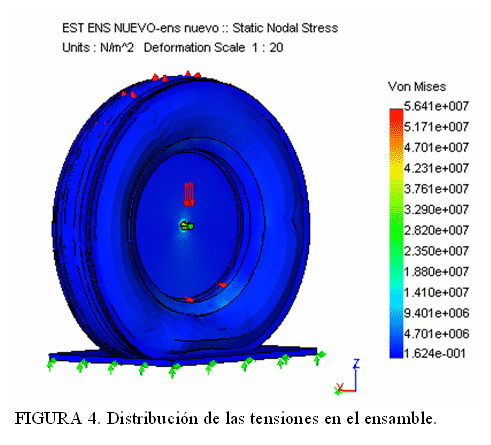
En la Figura 4 se muestra la distribución de tensiones equivalentes (Criterio de Von Mises) en el ensamble para una carga aplicada de 10 000 N, pudiendo apreciarse que las tensiones máximas no superan los 60 MPa.
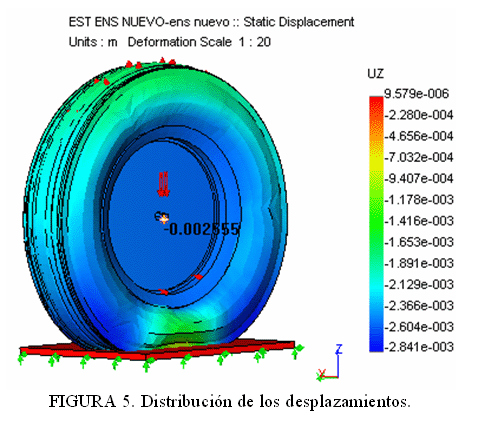
La Figura 5 muestra una vista isométrica de la deformación que sufre el ensamble bajo la carga aplicada en el eje Z. El valor de la deformación máxima correspondió a 0,284 cm, produciéndose un desplazamiento del eje del neumático de 0,255 cm como se aprecia en la figura.
En la Tabla 5 se muestran los resultados de la determinación de tensiones y desplazamientos en el neumático típico de máquinas agrícolas, bajo la acción de cargas estáticas mediante análisis por elementos finitos.
TABLA 5. Resultados de tensiones y deformaciones
Resultados de la determinación de coeficientes de cargas dinámicas en modelos objeto de estudio.
En la Figura 6 se muestra la corrida del software para obtener el resultado del coeficiente de carga dinámica en el neumático de máquinas agrícolas. En la figura se aprecia que para un rango evaluado (H=0…5 cm) el coeficiente de cargas dinámicas kd en el objeto de estudio (neumático típico de máquinas agrícolas), asume valores entre 2 y 7,336.
Multiplicando el coeficiente obtenido para cada altura del impacto, por la tensión o la deformación estática, entonces se determinan las tensiones o deformaciones en condiciones dinámicas.
FIGURA 6. Resultados del cálculo de coeficientes de cargas dinámicas por métodos tradicionales para neumático típico de máquinas agrícolas.
Después de haber analizado los resultados del cálculo de coeficientes de cargas dinámicas, podemos interpretar que; si la estructura no contara con el neumático de máquinas agrícolas (7.50-20-6), con una deflexión estática máxima del eje de 3,99 mm y una altura de impacto de 5 cm el coeficiente de cargas dinámicas es de 6,1 (Flores, 2009). Cuando posee el neumático sin ningún otro elemento de amortiguación, el coeficiente de cargas dinámicas para la misma altura del impacto y una deflexión estática de 6,54 mm, es de 5,03; por lo que se redujo un 1,07. Se determino que el neumático típico de maquinas agrícolas (7.50-20-6), redujo los coeficientes de cargas dinámicas para el remolque agrícola de 4t en un 17,54%.
CONCLUSIONES
• Los desplazamientos estáticas obtenidas mediante el análisis por elementos finitos fueron de 0,255 cm en el eje del neumático para una presión de inflado de 3,10 kg/cm2.
• El neumático típico de maquinas agrícolas (7.50-20-6) con una presión de inflado de 3,10 kg/cm2 fue capas de reducir en un 17,54% los coeficientes de cargas dinámicas del remolque agrícola de 4 t.
• Esta reducción de los coeficientes de cargas dinámicas implica, en el caso y las condiciones objeto de estudio, determinar si se producirá o no el fallo por fluencia del puente trasero del remolque analizado, cuando se introduce la acción amortiguadora de los neumáticos.
REFERENCIAS BIBLIOGRÁFICAS
1. AUBEL, T.H.: Simulationsverfahren zur untersuchung der wechselwirkung zwischen reifen und nachgiebiger fahrbahn auf der basis der Finite Elementhe Methode, Tesis (en opción al grado científico de Doctor en Ciencias Técnicas), Instituto de Ingeniería Automotriz de la Universidad de las Fuerzas Armadas, Hamburgo, 1994.
2. BOLARINWA, E.O. and A OLATUNBOSUN: Finite element simulation of the tyre burst test, Proc. Instn Mech. Engrs Part D: J. Automobile Engineering, Vol. 218, 2004.
3. BURR A.H. and J.B.CHEATHAM. Mechanical Analysis and Desing, 2ª edicion, cap. 14, Prentice hall: Englewood Cliffs, N.J. USA, 1995.
4. COLEMAN, G.E. and J.V. PERUMPRAL: The finite element analysis of soil compaction, Transaction of ASAE, 17: 856-860, 1974.
5. FERVERS, W.: Phänomene von luftreifen und Geländeböden–Untersuchungen mit FEM. 210pp., Tesis (en opción al grado científico de Doctor en Ciencias), Universität der Bundeswehr Hamburg–Institut für kraftfahrwesen und kolbenmaschinen, Editorial Shaker Verlag, Hamburg, 1999.
6. FLORES, R y A. MARTÍNEZ: “Análisis por elementos finitos de cargas de impacto. Estudio de caso de viga de tren de rodaje de remolque agrícola”, Revista Ciencias Técnicas Agropecuarias, 18(4): 21-27, 2009.
7. GOITIZOLO, R.; L. VILLA; E. ZAYAS; P.M. HERNÁNDEZ; J.G. NOA y H. HERNÁNDEZ: “Modificación del Alto Despeje del Tractor YUMZ 6M”, Revista Ciencias Técnicas Agropecuarias, 16(4): 11-16, 2007.
8. KAZUYUKI, K.; K. MASATAKA; R. YOKOHAMA; OIWAKE, HIRATSUKA: Tire cornering simulation using finite element analysis. Computational Mechanics Lab. Research and Development Center, Co., 2-1, Kanagawa 254-8601, Japan, 2000.
9. MARTÍNEZ, R. A; R. FLORES y J. SAMÁ: Influencia de la masa del cuerpo impactado sobre los coeficientes de cargas dinámicas calculados por métodos tradicionales, Revista Ciencias Técnicas Agropecuarias, 18(2): 22-26, 2009.
10. NACKENHORST, U.; M. ZIEFLE: Finite element modelling of rolling tires. Universität Hannover, Institut für Baumechanik und Numerische Mechanik Allemagne, 58(6):322-326, 2005.
11. PERUMPRAL, J.V.: The finite element method for predicting the stress distribution and soil deformation under tractive device. Tesis (en opción al grado científico de Doctor en Ciencias). Purdue University, Lafayette, Indiana, 1969.
12. PERUMPRAL, J.V.; J.B. LILJEDAHL; W.H. PERLOFF: The finite element method for predicting the stress distribution and soil deformation under a tractive device. Transaction of ASAE, 14: 1184-1188, 1971.
13. PISARENKO, G.S.: Manual de Resistencia, 2ª Reimpresión, Moscú, URSS, 1989.
14. ROARK, R.J. and W.C. YOUNG: Formulas for stress and Strain 6ª Edición, McGraw-Hill: Nueva York, 1989.
15. SCHMID, I.: “Interaction of vehicle and terrain results from 10 years research at IKK”. Journal of terramechanics, 32(1): 3-26, 1995.
16. SHOOP, A.S.: Finite element modeling of tire terrain interaction, US Army Corps of Engineers, erdc/crrel tr, 01-16, 2001.
17. YONG, R.N.; E.A. FATTAH and R. BOOSINUK: Prediction of wheel-soil interaction and performance using the finite element method, Journal of Terrramechanics, 15(1):43-63, 1978.
18. YONG, R.N. and E.A. FATTAH: Prediction of wheel-soil interaction and performance using finite element method, Journal of Terramechanics,13(4): 227-240, 1976.
Recibido 04/04/09, aprobado 21/07/10, trabajo 48/10, investigación.













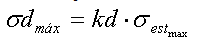 (1)
(1)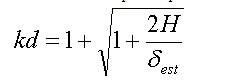 (2)
(2)