ARTÍCULO ORIGINAL

 

Metodología para determinar la fuerza de arrastre de productos agrícolas a partir de la Dinámica de Fluidos Computacional (CFD)

 

Methodology to determine the drag force in agricultural products under computer fluid dynamic tools (CFD)

 

 

Alexander Laffita Leyva, Arturo Martínez Rodríguez, Vilma Toledo Dieppa, Yolanda Sabín Rendón, Pedro A. Valdés Hernández

Universidad Agraria de La Habana, Facultad de Ciencias Técnicas, Centro de Mecanización Agropecuaria, San José de las Lajas, Mayabeque, Cuba.

 

 

---

RESUMEN

El objetivo del trabajo consiste en obtener una metodología para la determinación, con el apoyo de herramientas de la Dinámica de Fluidos Computacional (CFD), de la fuerza de arrastre en productos agrícolas u otro tipo de sólido sometidos a una corriente de aire. Conociendo la distribución de presiones en la superficie y las coordenadas de posición de los nodos de la malla de elementos finitos generada, se elabora una metodología matemática, sobre la base de la geometría analítica y vectorial, que permite determinar la fuerza de arrastre que actúa sobre el modelo digitalizado.

Palabras clave: elementos finitos, corriente de aire, método matemático.

---

ABSTRACT

The objective of the work consists on obtaining a methodology for the determination, with the support of the Dynamics of Flowing Computational (CFD) tools, of the haulage force in agricultural products or another solid type subjected to a draft. Knowing the distribution of pressures in the surface and the coordinates of the nodes position of the finite elements´ generated mesh, a mathematical methodology is elaborated, on the base of the analytic and vectorial geometry that allows determining the haulage force that acts on the digitized pattern.

Key words: finite elements, air stream, mathematical method.

---

 

 

INTRODUCCIÓN

Por su importancia las propiedades físico–mecánicas de granos de productos agrícolas han sido abarcadas por diferentes autores con el objetivo de diseñar instalaciones para el almacenamiento, secado y transporte en equipos industriales. Mohsenin, (1980); Molenda et al., (1998), según refieren Jouki & Khazaei, (2012), en la tasa de intercambio de calor y masa durante el proceso de secado influyen fundamentalmente la densidad, el coeficiente de fricción estático, el ángulo de fricción interno y las características dimensionales de los granos.

Para evaluar el comportamiento aerodinámico de productos agrícolas se utilizan dos vías: experimental y la simulación por software especializados. La primera requiere el uso de un túnel de viento aerodinámico, utilizados, además, por las industrias aeroespacial, y automovilística, entre otras disciplinas. El mismo permite estudiar el comportamiento del aire cuando un objeto se encuentra en el interior del flujo, obteniéndose datos de presiones, fuerzas, visualización de las líneas de corriente, entre otras (Farrarons, 2005). Así mismo tiene la ventaja que permite tener controladas las variables termodinámicas del aire: densidad, temperatura y presión, requiriendo de instalaciones relativamente grandes y complejas que repercute directamente en los costos. Por otro lado, las técnicas de análisis por el método de la dinámica de fluido computacional poseen: bajo costo, simplicidad, facilidad y disminución del tiempo de duración de la investigación, pudiendo ser comprobados posteriormente por el método experimental como vía de validación.

Sarker et al., (1989); Lu y Sibenmorgen, (1992); Yang et al., (2003), citados por Bhagwati & Zhongli, (2011) investigaron, aplicando el método de los elementos finitos, el comportamiento del gradiente de humedad durante el proceso de secado de granos de arroz.

Para hallar la fuerza resultante actuante sobre el grano se deben conocer las presiones sobre su superficie. Con el apoyo de herramientas de la Dinámica de Fluidos Computacional (CFD) se obtiene el campo de velocidades y presiones actuantes sobre el modelo en función de las condiciones fronteras. Vu-Quoc et al. (2000) y Gorham & Salman (2005), según reportan Medina et al. (2010), desarrollan modelos matemáticos: el primero para el transporte de partículas elipsoidales en conductos en forma de paralelepípedo, mientras que el segundo para el acarreo neumático en conductos horizontales de partículas esféricas, desarrollando Gorham & Salman (2005) un algoritmo, empleando el método de los elementos finitos, para modelar el comportamiento de un grano de soya sometido a una corriente de aire vertical.

Couto et al. (2004), desarrollan una metodología sobre la base de subdividir en elementos finitos de área, anillos de la superficie de un fruto de café, tomando como valor promedio la presión en 37 puntos ubicados en los bordes extremos del anillo. Posteriormente determinan, para incrementos en la dirección del eje x según se muestra en la Figura 1, el valor de la fuerza de arrastre que ejerce el fluido sobre el fruto.

Existe en la literatura valores establecidos de coeficientes de arrastre para determinadas formas geométricas (NASA, 2014; Drag Coefficients, 2014a; Drag Coefficients, 2014b). El mismo no es una constante absoluta para una geometría dada de un cuerpo. Este coeficiente varía con la velocidad del flujo o de manera más general, con el número de Reynolds, la dirección del flujo, la posición del objeto, el tamaño del objeto, la densidad del fluido y la viscosidad del mismo. Empleando herramientas de Dinámica de Fluidos Computacional, basadas en el empleo del Método de Elementos Finitos, por lo general, es posible obtener la fuerza de arrastre que ejerce un fluido sobre un cuerpo (Staffan, 2006).

Sin embargo, los trabajos anteriores no proporcionan una metodología que permita determinar la fuerza de arrastre que ejerce el fluido sobre un cuerpo a partir, de conocer el campo de presiones actuantes sobre el modelo obtenido de las herramientas CFD, por lo que es necesario su desarrollo.

 

MÉTODOS

A partir de que el programa computacional divide en elementos tetraédricos de cuatro nodos el modelo en estudio, se utiliza como elementos de entrada para el desarrollo de la metodología, las coordenadas de cada nodo extremo, combinaciones de nodos que conforman los elementos en la superficie analizada y los valores de presión actuante en cada nodo del área analizada del cuerpo solido. En la Figura 2 se muestra los elementos finitos de área triangulares con el objetivo de determinar los baricentros de los triángulos de superficie sobre el que actúan las presiones resultantes en cada nodo o vértice del triángulo. Teniendo en cuenta la condición de simetría de algunos productos agrícolas se puede modelar la mitad de la geometría en cualquier software de modelación de sólidos.

En la Figura 3 se muestra una ampliación de un elemento finito de área, en donde se identifica un ordenamiento de la numeración local de los nodos elementales identificados como P1; P2; P3, los vectores de posición con origen en el sistema de coordenadas hacia los nodos y hacia el baricentro . De este último sale el vector unitario o versor que son utilizados para identificar la dirección normal a la superficie.

Las coordenadas del baricentro, vector unitario, elemento finito de área de la superficie y componentes vectoriales de la fuerza sobre el baricentro, se determinan aplicando los fundamentos de la geometría analítica y vectorial (Lehmann, 1974), lo cual se desarrolla a continuación:

Determinación de las coordenadas del baricentro (B)

A partir del conocimiento de los vectores de posición de los nodos extremos del elemento triangular de superficie, se pueden determinar las coordenadas (X_B;Y_B;Z_B) del baricentro (B) del elemento de superficie según la expresión:

donde:

X_i ;Y_i ; Z_i - coordenadas de los nodos que conforman el triángulo.

Determinación de las componentes del vector unitario que sale del baricentro

El vector unitario se determina como el cociente entre un vector normal u ortogonal a la superficie y su norma o módulo según la expresión:

Los vectores con origen en el baricentro hacia dos nodos del triángulo se determinan por las siguientes expresiones:

El producto vectorial de dos vectores con origen en el baricentro hacia dos nodos del triángulo nos permite determinar el vector ortogonal como:

Este producto se desarrolla mediante una matriz de determinante de orden tres como:

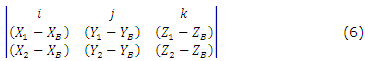
Las componentes del vector ortogonal se obtienen resolviendo la matriz aplicando el método de menores de la siguiente forma:

Determinación de las componentes del vector fuerza de arrastre actuando sobre el baricentro

A partir de conocer los valores de la presión resultante actuando en el baricentro (P_Rb), el vector unitario asociado a este y el elemento finito de área (A) del triángulo, pueden determinarse las componentes de la fuerza de arrastre resultante actuando en el baricentro del triángulo como:

Conociendo el valor de la presión de cada nodo en ese pequeño dominio triangular se obtiene la presión resultante actuando en el baricentro de la siguiente forma:

Aplicando la expresión de Herón (Lehmann, 1974) se determina el área (ΔA) de la cara triangular del elemento finito contenido en la superficie, mediante:

donde:

p. -semi-perímetro del triángulo, mm;

a; b; c. - distancia de cada lado del triángulo, mm.

El semi-perímetro se determina como:

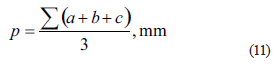
Mediante las coordenadas de cada nodo del triángulo se determinan las distancias de cada lado mediante las expresiones:

En la Figura 4 se muestra el sentido, dirección y punto de aplicación de la fuerza de arrastre resultante actuando en el baricentro de un triángulo opuesto al sentido del vector unitario.

El vector de la fuerza de arrastre total actuante sobre el cuerpo se obtiene mediante la sumatoria de las componentes vectoriales de la fuerzas de arrastre resultantes en el baricentro de cada uno de los triángulos de la superficie analizada del mismo, quedando finalmente la sumatoria de las componentes de la fuerza de arrastre total en la dirección de la velocidad del aire, al anularse las otras dos componentes radiales por la condición de simetría.

 

CONCLUSIONES

La metodología propuesta, sobre la base de la geometría analítica y vectorial, permite obtener la fuerza de arrastre total que ejerce el fluido sobre la superficie a analizar de un cuerpo sólido, a partir de conocer las coordenadas de cada nodo extremo de los diferentes elementos finitos de área en que se subdivide el modelo, las combinaciones de nodos que lo conforman y los valores de presión actuantes en cada nodo.

 

 

REFERENCIAS BIBLIOGRÁFICAS

1. Drag Coefficients [en línea], Disponible en: http://web.archive.org/web/20070715171817/http://aerodyn.org/Drag/tables.html [Consulta: 10 de diciembre de 2014a].

2. BHAGWATI, P. & P. ZHONGLI: Modeling Moisture Movement in Rice, Edited by University of California, USDA, United States, 2011.

3. Drag Coefficient: [en línea], Disponible en: http://www.engineeringtoolbox.com/drag-coefficient-d_627.html [Consulta: 10 de diciembre de 2014b].

4. GORHAM, D. A. & D. SALMAN: “The failure of Spherical particle under impact”, Wear magazine, 258 (1-4): 580-587, 2005.

5. LEHMANN, H. CH.: Geometría Analítica, Instituto Cubano del Libro, Editorial pueblo y educación, 2da Edición, La Habana, Cuba, 1974.

6. JOUKI, M & N. KHAZAEI: Some Physical Properties of Rice Seed, Faculty of Agricultural Engineering, University of Urmia, Iran, 2012.

7. LU, R. & J. SLEBENMORGEN: “Moisture diffusivity of long-grain rice components”, Transactions of the ASAE, 35(6), 1955-1961, 1992.

8. COUTO, M. S.; O. DOS SANTOS; M.J. VIEIRA; P. DA SILVA: “Determinacao da forca de arrasto e da velocidade terminal de frutos de café pela técnica de elementos finitos”, Rev. bras. eng. agríc. ambient. [en linea] 8(2-3) Campina Grande, Brasil, 2004. , ISSN 1807-1929. Disponible en: http://dx.doi.org/10.1590/S1415-43662004000200017 [Consulta: enero 2013].

9. MEDINA, M; M. MATTARA Y R. PONSO: Modelización para el cálculo de velocidades de acarreo del aire en el transporte de granos de soja, Ed. Avances en Energías Renovables y Medio Ambiente, 14, Argentina, 2010.

10. MOHSENIN, N. N.: Physical Properties of Plant and Animal Materials, New York, USA, 1980.

11. MOLENDA, M; SZOT, B. & A. FERRERO: “Binding force and mechanical strength of rice grain”, Int. Agrophysics, [version electrónica] (12): 227-230, 1998.

12. NASA: Modern Drag Equation. [en línea], Disponible en: http://wright.nasa.gov/airplane/drageq.html [Consulta: 10 de diciembre de 2014].

13. SARKER, N. N & N. FAROUK: “Some Factor Causing Rice Milling Losses in Banggladesh”, Agric. Mech. in Asia, Africa and Latin America, 20(2), 40-49, 1989.

14. STAFFAN, H.: Drag Estimations on experimental aircraft using CFD, 10pp., Ed. MDH.IMA. FLY. 0180. 10p., 2006.

15. VU-QUOC, L.: “Discrete element method for dry granular flows of ellipsoidal particles", Mech. Eng., (187): 483-528, 2000.

16. YANG, W. JIA & C. HOWELL: “Relationship of Moisture Content Gradients and Glass Transition Temperatures to Head Rice Yield during Cross-Flow Drying”, Biosystems Engineering, 86(2): 2003.

 

 

Recibido: 6 de enero de 2014.
Aprobado: 22 de julio de 2014.

 

 

Alexander Laffita Leyva. Universidad Agraria de La Habana, Facultad de Ciencias Técnicas, Centro de Mecanización Agropecuaria, San José de las Lajas, Mayabeque, Cuba. Correo electrónico: [e-mail]