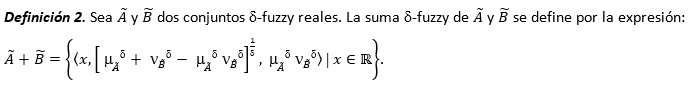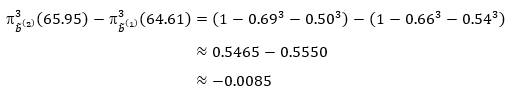Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Corría el año 1944, justo en los inicios de la Guerra Fría, cuando el general Henry Harley Arnold encargó un informe para la U.S. Army Air Corps, sobre las capacidades tecnológicas del futuro que podrían servir de uso militar. Dos años más tarde, surgió la Corporación RAND, un laboratorio de “tanques pensantes” dedicado, por aquellos tiempos, al estudio de conflictos bélicos intercontinentales. Este contexto fue el inicio del proyecto “Delphi”, denominación inspirada en el célebre oráculo griego erigido al dios Apolo. También fue el comienzo de un largo e intermitente proceso de desarrollo de un método prospectivo denominado, precisamente, “método Delphi” (Keeney, et al., 2011).
Investigadores de la RAND observaron que los métodos tradicionales de pronóstico mostraban una efectividad limitada, justo en escenarios renovadores de construcción de futuro. Allí el procesamiento de información normalizada, como en el caso de series cronológicas, no resulta viable (Dalkey & Helmer, 1963). Para superar estos obstáculos, los primeros estudios desarrollaron una teoría del concepto de “experto predictivo”, donde confluye el pensamiento racional y reflexivo con la noción de “probabilidad personal”, una especie de medida de la confianza individual o convicción subjetiva acerca de la verdad de una hipótesis (Helmer & Rescher, 1958).
Tampoco el empleo del conocimiento experto, por sí solo, resultó efectivo. Investigaciones psicológicas de la primera mitad del siglo pasado ya advertían sobre ciertas deficiencias, vinculados con las técnicas grupales. Por ejemplo, la influencia de individuos dominantes, el ruido, el efecto “halo”, y la conformidad relacionada con la presión social (Cruz, 2009). A raíz de ello, en 1953 Dalkey & Helmer (1963), introducen características adicionales que determinan el método Delphi. Al decir de estos autores, en su versión convencional, el objetivo consiste en “obtener el consenso de opinión más confiable de un grupo de expertos” (Dalkey & Helmer, 1963, p. 458). Son tres los rasgos definitorios: anonimato de un panel de expertos, aplicación iterada de encuestas con retroalimentación controlada, y respuesta estadística de grupo (Cruz, et al., 2020).
Con el paso del tiempo, el método Delphi sobrevivió a críticas incisivas y también experimentó modificaciones amplias y heterogéneas, conducentes a una amplia tipología: e-Delphi, Delphi fuzzy, Delphi de nube, mini-Delphi, max-min Delphi, Delphi online, entre numerosas variantes descritas en la literatura (Hasson & Keeney, 2011). Estudios cienciométricos recientes no solo reflejan esta diversificación, sino también la extensión hacia campos disímiles de la ciencia y la tecnología, e incluso el mejoramiento sistemático del propio método (Flostrand, et al., 2020).
También el método Delphi ha cobrado impulso significativo con base en las matemáticas. Probablemente, el caso más emblemático ha consistido en el enfoque proveniente de los conjuntos fuzzy. Ejemplos recientes dan cuenta de ello, como el caso del Delphi difuso (Kumar & Dash, 2017; Lee & Seo, 2015), el Delphi difuso intuicionista (Roy & Garai, 2012; Rajaprakash & Ponnusamy, 2015), el Delphi difuso pitagoreano (Özkan, et al., 2020), y el Delphi indeciso borroso (Jafarnejad, et al., 2019).
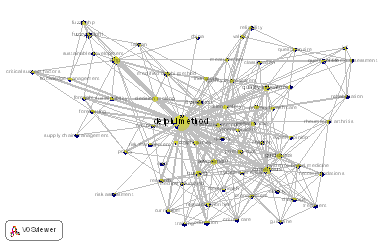
La Fig. 1 refleja el procesamiento con VOSviewer de las palabras claves de más de 11 mil documentos referenciados en Scopus, relacionados con el método Delphi durante el periodo 1960-2019 (se visualizan los términos observados al menos 30 veces). La palabra clave “fuzzy Delphi” forma un pequeño clúster vinculado a la toma de decisiones, al pronóstico, a la gestión de cadenas de suministro, a los factores críticos de éxito, a los AHP (procesos analítico-jerárquicos, por sus siglas en inglés), al desarrollo sostenible, entre otros aspectos.
Llaman la atención dos aspectos particulares: primero, que el clúster contentivo del enfoque fuzzy se encuentra relativamente desvinculado del resto de los conceptos afines al empleo del método Delphi (ver parte superior izquierda de la Fig. 1) y, segundo, que la conexión más fuerte del Delphi fuzzy se establece con los estudios AHP. El gráfico refleja las 300 relaciones más fuertes. Si este número se incrementa añadiendo otras 200 relaciones menos fuertes, apenas se observa un vínculo entre el clúster mencionado y los conceptos de fiabilidad y validez, ubicados en la parte superior de la figura. Todo ello aporta evidencia acerca de un énfasis marcado en los componentes matemáticos y tecnológicos, en detrimento de otros aspectos teóricos estrechamente vinculados al método Delphi, tales como el consenso y la evaluación.
El presente trabajo tiene el objetivo de presentar un enfoque fuzzy generalizado para el Delphi de pronóstico, el cual comprende una clase amplia y con oportunidades de desarrollo de órdenes teórico y práctico. A continuación, se presentan elementos básicos de los conjuntos (-fuzzy, que constituyen un camino de generalización del enfoque borroso intuicionista. Seguidamente, se desarrolla el método Delphi de tipo pronóstico, con base en los conjuntos (-fuzzy. Finalmente, se ejemplifican los resultados, en el marco de un pronóstico real de resultados académicos.
Un conjunto (-fuzzy constituye una generalización de los conjuntos difusos clásicos (Zadeh, 1965), intuicionistas (Atanassov, 2012), y pitagoreanos (Yager, 2013). Este concepto ha sido desarrollado de manera reciente, con un enfoque predominantemente matemático. Las aplicaciones descritas en la literatura todavía no son suficientemente ilustrativas de las amplias posibilidades de desarrollo teórico y empírico. El Delphi de tipo pronóstico, generalmente requiere de métodos matemáticos poco sofisticados. La estimación de una fecha probable para cierto acontecimiento, o bien la estimación de un resultado, implican el cálculo de estadígrafos elementales relacionados con los valores empíricos que sugieren los expertos ronda tras ronda. Esta versión ha sido objeto de críticas, en el sentido de que el hecho de solicitar una estimación puntual, pone al experto en una situación embarazosa. Ya el enfoque fuzzy clásico ha superado este problema, desde el mismo momento en que se le pide al experto un intervalo probable y no un valor puntual. Sin embargo, existen situaciones que requieren de modelos matemáticos más generales.
Seguidamente se presentan cinco conceptos necesarios para llevar a término el presente estudio. Aunque se trata de elementos básicos que están lejos de describir los avances existentes en este campo, sirven para erigir el método Delphi con un enfoque difuso más general, específicamente en el campo del pronóstico. En primer lugar, se requiere de un concepto de conjunto difuso generalizado, el cual se denominará (-fuzzy. Luego se mostrará cómo operar con tales conjuntos y cómo medir la distancia entre ellos. Seguidamente, se presentará una generalización de números (-fuzzy, similar a la idea de número difuso triangular como caso especial de conjunto difuso clásico. Para concluir, se introduce la noción de promedio (-fuzzy de los números antes definidos. Las primeras cuatro definiciones han sido tomadas de estudios recientes (Shabani & Jamkhaneh, 2014; Jamkhaneh & Nadarajah, 2015). La última constituye una generalización natural del concepto de media artimética (-fuzzy (Jamkhaneh & Garg, 2017).
De esta definición se derivan directamente los conjuntos difusos intuicionistas para (=1, los pitagoreanos para (=2, etcétera. Es obvio que si ( 1 < ( 2 entonces, todo conjunto ( 1 -fuzzy es también ( 2 -fuzzy. Para los objetivos del presente estudio será necesaria la operación de suma entre conjuntos (-fuzzy y el cálculo de la distancia entre conjuntos (-fuzzy donde el universo de discurso es el conjunto de los números reales.
Puede verificarse que esta operación suma es una ley interna que cumple los axiomas correspondientes a una 𝑡-conorma, mientras que el conjunto potencia del universo, provisto de la operación suma constituye un monoide abeliano.
En el caso real, puede demostrarse con relativa sencillez que si el universo de discurso es acotado (por ejemplo, un intervalo real), entonces se cumple que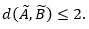 
Los conjuntos (-fuzzy adquieren mayor significado a partir de sus aplicaciones prácticas. Por ejemplo, existen situaciones tales como los sondeos electorales, donde suele quedar cierto margen para la incertidumbre. Así, en los conjuntos difusos intuicionistas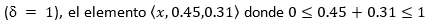 
puede significar que el candidato 𝑥 tiene un 45% de intenciones de voto a favor, un 31% en contra, mientras que resta el margen de un 24% de electores indecisos. Por su parte, en las escalas de actitud, cuando una persona expresa su preferencia acerca del grado en que una alternativa satisface cierto criterio, su reflejo subjetivo de la situación contraria no necesariamente se expresa de forma excluyente. Yager (2013), presenta algunos ejemplos donde el modelo intuicionista no explica las evidencias empíricas, sin embargo sirve de soporte el modelo pitagoreano (( = 2). De forma general, el enfoque (-fuzzy asegura una amplia clase de posibilidades.
Desde el punto de vista práctico, en las aplicaciones se utilizan los conjuntos difusos triangulares, los cuales constituyen casos particulares muy simplificados que pueden denominarse “números”. Asimismo, en el presente trabajo se emplearán números (-fuzzy triangulares definidos por Shabani & Jamkhaneh (2014).
Definición 4. Un número (-fuzzy triangular es un conjunto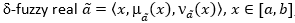 
, donde las funciones de pertenencia y de no pertenencia vienen dadas respectivamente por las expresiones:
En vista de que la aplicación del método Delphi de tipo pronóstico suele requerir del cálculo de promedios, será necesario también utilizar una generalización (-fuzzy del concepto de media aritmética.
Puede demostrarse que el promedio 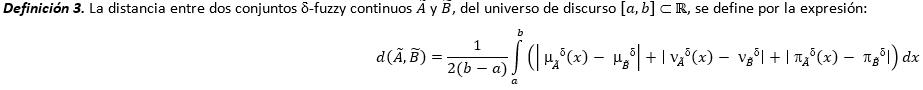es también un número (-fuzzy triangular. Ahora, a partir de un conjunto finito de números (-fuzzy triangulares, es posible construir un promedio, cuyo dominio constituye una tripla de medias aritméticas, mientras que su imagen expresa una dupla de medias aritméticas, cuadráticas, cúbicas, etcétera, conforme a 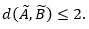respectivamente. Con estas herramientas matemáticas, es posible establecer la base estructural y funcional de un Delphi (-fuzzy.
Tal como se señaló anteriormente, el método Delphi se define esencialmente por medio de tres rasgos distintivos. Sin embargo, son varios los modos de implementación donde sus características se expresan de forma concreta, muchas veces adaptadas a condiciones específicas de cada investigación. De forma general, este método posee sendos componentes personal y estructural-funcional. En el primero de ellos concurren dos actores fundamentales: el panel de expertos y un grupo coordinador que funge como responsable en la conducción del proceso. Este grupo define los objetivos a cumplir, selecciona los integrantes del panel, prefija la condición de parada sobre el conjunto de rondas, elabora los cuestionarios y precisa la información que devuelve al panel, y toma decisiones a partir de los resultados finales, previo análisis y discusión acerca de la calidad del proceso y del cumplimiento de los objetivos trazados. Algunas veces, en lugar de un grupo figura un único investigador respondiendo a motivos prácticos, pero ello tiene el inconveniente de poner en riesgo la parsimonia y objetividad necesarias en el análisis/síntesis de la información que aportan los expertos. La Fig. 2 contiene un flujograma donde se ilustran las relaciones entre los componentes señalados.
El flujograma expresa algunos tipos de relaciones que han sido ponderadas en estudios dirigidos al mejoramiento del método Delphi. Por ejemplo, antes de cada ronda es conveniente mejorar la fiabilidad y validez de los cuestionarios, aplicando un pilotaje en el estrato remanente de expertos potenciales que fueron desestimados tras la aplicación del dispositivo de selección. Asimismo, resulta gratificante empoderar a todos los expertos, al proveerles información de los resultados finales que resulte de su interés.
Cada una de las fases de preparación, desarrollo de rondas, procesamiento y conclusión, tienen sus propias particularidades y niveles de complejidad. En la primera de ellas, el flujograma sugiere la confección de instrumentos para el cálculo de índices de competencia experta. Este no es el único mecanismo de discriminación, pero suele resultar bastante práctico. Sin embargo, la elaboración implica el diseño, donde existen problemas epistémicos relacionados con el concepto de experticia, problemas de selección y ponderación de indicadores de medida, así como problemas en la determinación de un punto de corte sobre la escala de experticia (Cruz, 2009). El propio establecimiento de la condición de parada constituye un problema muchas veces solapado bajo la fijación anticipada y espontánea del número de rondas. En general, el criterio de finalización del proceso responde a medidas de consenso, de estabilidad, a la proporción del número de expertos que modifican su respuesta, entre otros aspectos que han sido analizados en estudios experimentales (Landeta, 1999).
En el presente trabajo, resulta de interés la etapa de procesamiento que aparece mediada por subprocesos de codificación y decodificación (-fuzzy. El procedimiento aplicado para la toma de decisiones responde a los objetivos específicos de cada investigación y depende, en mayor medida, a la naturaleza de los datos. Por ejemplo, en estudios prospectivos de tipo “almanaque”, regularmente los cuestionarios demandan la estimación de un conjunto de fechas eventuales, así que el procesamiento seguirá un enfoque borroso solo en aquellos casos en que esto haya sido previsto durante el diseño de los cuestionarios.
Por otro lado, el Delphi de pronóstico constituye una de las variantes más sencillas, pero a la vez más útiles por su marcada naturaleza prospectiva. Con base en el flujograma de la Fig. 2, la versión (-fuzzy del Delphi de pronóstico se caracteriza por las siguientes particularidades:
En la fase de preparación se prefija la escala de cada variable a pronosticar. Generalmente se emplean escalas de razón, donde se conservan invariables las longitudes entre segmentos, las proporciones tienen sentido, y existe un punto especial que sirve de cero absoluto.
Durante las rondas Delphi, generalmente se mantiene el mismo cuestionario, enfocado a la determinación de la fecha más probable en que tendrá lugar un evento objeto de estudio. Por este motivo, el pilotaje se realiza solo en el estadio inicial. El diseño de los cuestionarios debe tener suficiente sensibilidad, de manera que el instrumento logre captar todos los valores que definen un número (-fuzzy triangular. La retroalimentación controlada, por su parte, consiste en informar al panel acerca del valor medio de las fechas propuestas en cada ronda precedente. También puede proveerse información adicional, relacionada con estadígrafos de dispersión.
Al transcurrir la fase de procesamiento, existen dos etapas esenciales que singularizan este tipo de estudio: la codificación y decodificación (-fuzzy. En la primera se determina el valor ( mínimo para establecer el modelo matemático adecuado. Con ello, se construyen los correspondientes números (-fuzzy triangulares, los cuales son procesados con ayuda de las herramientas matemáticas definidas anteriormente. En la segunda etapa se interpretan los resultados, conforme a las variables objetivas de investigación. La condición de parada está relacionada con la noción ideal de consenso, que puede medirse con base en la distancia (-fuzzy entre promedios de rondas consecutivas.
La fase conclusiva constituye la expresión materializada del procesamiento Delphi. En el caso del pronóstico (-fuzzy, la toma de decisiones debe considerar en qué medida el modelo matemático empleado se ajusta a las evidencias empíricas.
Seguidamente se presentan los resultados de un ensayo experimental, donde se ilustra la necesidad del enfoque (-fuzzy durante un Delhpi de tipo pronóstico.
Materiales y métodos
En el presente trabajo se implementa un estudio Delphi de tipo pronóstico con enfoque (-fuzzy en la Universidad de Holguín (Cuba), durante la aplicación de una prueba de ingreso a la educación superior en la asignatura de Matemática. Este tipo de examen se realiza a escala nacional desde hace más de 30 años, con el fin de elevar la calidad del ingreso a las universidades del país. La Fig. 3 contiene una encuesta dirigida a especialistas que fueron seleccionados para calificar este tipo de examen. Las tres primeras preguntas tratan de captar el pronóstico de los expertos (expresado en porciento), de forma similar al enfoque difuso clásico, con sendos valores mínimo y máximo junto al valor más probable. Las dos últimas preguntas tratan de captar el grado de certidumbre/incertidumbre de cada experto, respecto a su propia opinión.
Las tres primeras preguntas refieren valores porcentuales aproximados, enmarcados en el intervalo real [0, 100]. Para las dos últimas, a cada casilla marcada se le hace corresponder respectivamente un valor discreto 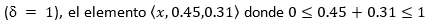de izquierda a derecha, como elementos modales que marcan estadios de cambio perceptible, dentro del intervalo real 
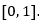Todas las preguntas refieren valores reales no negativos, de modo que la escala de cada variable correspondiente es de razón.
La encuesta se aplica en dos ocasiones: antes de tener acceso al examen y a su norma de calificación, y luego de tener acceso. De esta manera se espera observar ciertos cambios en el pronóstico individual y colectivo. La retroalimentación no proviene de un procesamiento sintético de la respuesta del panel, sino de la incidencia externa de una situación objetiva.
Para conformar los números (-fuzzy triangulares se procede de la siguiente manera. Las tres primeras respuestas corresponden, en su orden, a las componentes de cada dominio. Por ejemplo, si un experto responde respectivamente 60, 70 y 65 en la primera ronda, se tiene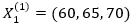 
. Los valores de las dos últimas respuestas refieren un mismo fenómeno, pero con enfoques diferentes. La cuarta pregunta es directa, de manera que su respuesta se identifica con el grado de pertenencia del valor más probable. Por el contrario, la quinta pregunta es indirecta, así que su complemento se identifica con el grado de no pertenencia del valor más probable. Con ello se forma la imagen de cada número (-fuzzy triangular, seleccionando el valor modal correspondiente a la casilla de la cuarta pregunta, y calculando la diferencia entre 1 y el valor correspondiente en la quinta pregunta. Finalmente, los resultados se procesan conforme a los conceptos matemáticos antes descritos.
Resultados y discusión
El estudio se desarrolló en el mismo escenario de calificación y en tiempo real. La distribución del instrumento la ejercieron directamente los responsables de la calificación de cada pregunta (en locales independientes). Estos especialistas recibieron una capacitación previa y fueron los encargados de explicar los objetivos de la investigación y las características del instrumento. La encuesta se aplicó a todo el equipo formado por 56 evaluadores (expertos), seleccionados de forma conjunta por la Universidad de Holguín y la Dirección Provincial de Educación para calificar más de 1400 estudiantes, en octubre de 2020.
Las respuestas en la primera ronda estuvieron condicionadas probablemente por vivencias previas de los evaluadores, donde el 78.6% posee experiencia en este tipo de actividad. Para ilustrar la codificación (-fuzzy expuesta en el flujograma de la Fig. 2, sirve de ejemplo las respuestas del primer experto, el cual estimó un mínimo del 50%, un máximo del 70% y un valor más probable del 62%, También marcó respectivamente la octava y la secta casillas de las dos últimas interrogantes, respectivamente, así que los valores modales son 0.7 y 0.6 en este orden. Por tanto,
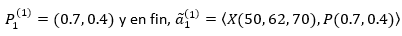. Está claro que las componentes de la imagen de 𝑎 1 1 no satisfacen el modelo borroso tradicional. Puede verificarse que el valor mínimo 
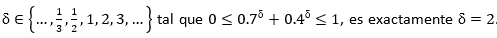. Por tanto, para el primer experto y en la primera ronda, sirve el modelo pitagoreano. Sin embargo, el valor de ( debe seleccionarse de manera que responda a todas las evidencias empíricas.
Después de inspeccionar globalmente los datos, se eliminan las respuestas de cuatro expertos, por no ser concordantes respecto al modelo. Por ejemplo, en la segunda ronda el sexto experto marcó el equivalente a un valor de pertenencia 
. Como puede apreciarse, en el primer caso no da margen a la incertidumbre y asegura que su respuesta será acertada, pero ello contradice lo expresado en el segundo caso, para todo valor ( en el modelo propuesto. En realidad, este tipo de respuesta es eventual y obedece a percepciones subjetivas del experto, el cual manifestó un cambio de apreciación. Su respuesta no es objeto de crítica, sino que se desecha ya que no puede ser explicada bajo el modelo matemático construido. En realidad, el valor mínimo encontrado para ambas rondas fue 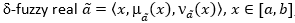, para al menos una quinta parte del panel de expertos.
El cálculo de los números (-fuzzy promedio, condujo a los resultados siguientes. En la primera ronda se obtuvo 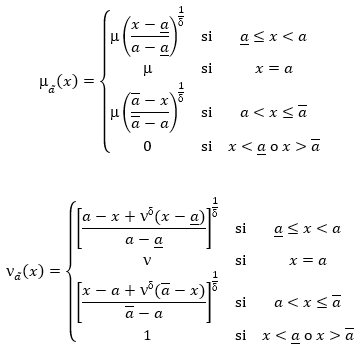, mientras que en la segunda ronda el resultado fue 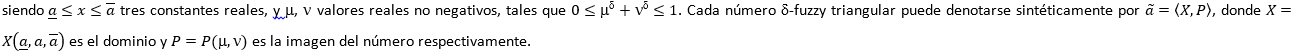. Las siguientes sentencias de GeoGebra facilitan la visualización y el cálculo de la distancia entre ambos números (-fuzzy triangulares, donde puede verificarse directamente que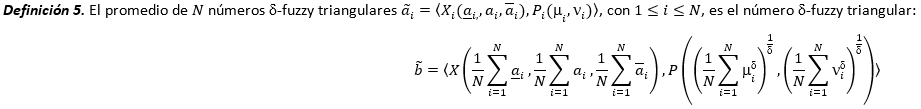
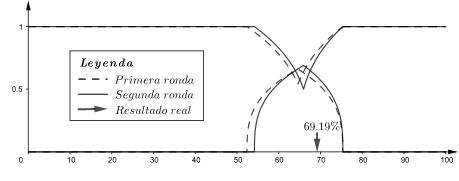
Los resultados de la visualización se ilustran en la Fig. 4
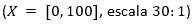. Con líneas discontinuas se representa la respuesta promedio 
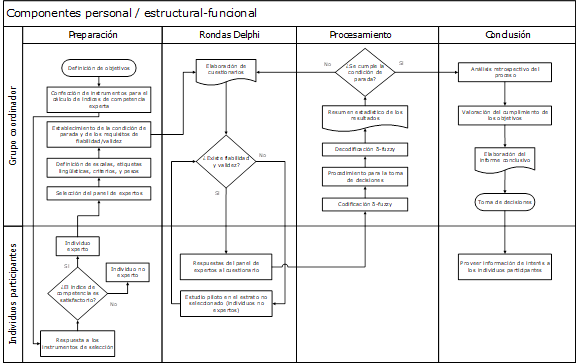en la primera ronda, y con líneas continuas se representa la respuesta promedio 
en la segunda ronda. Puede notarse que los límites superiores de ambos dominios cambian relativamente muy poco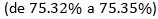 
. Sin embargo, el límite inferior alcanza un incremento perceptible de una ronda a otra 
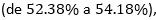y lo mismo ocurre con ambos valores medios .
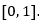Las evidencias empíricas sugieren que los expertos estimaron un rango admisible, basado en los resultados tradicionales obtenidos por la provincia durante los últimos años (aproximadamente 𝑋 =73.85 y (=5.81 en el último quinquenio). El cambio en el límite inferior responde, probablemente, a una percepción del examen con un grado de dificultad ligeramente inferior a lo esperado. A su vez, la rigidez experimentada en el límite superior puede ser el efecto de una actitud conservadora, motivada por los resultados históricos de la provincia en ese tipo de examen. Cabe destacar el hecho de que el resultado real obtenido en esta prueba de ingreso fue del 69.19 %, poco distante de la percepción prospectiva de los expertos.
Por otro lado, una mirada a las imágenes de ambos números 3-fuzzy triangulares revela otro tipo de cambio. Los máximos de las funciones de pertenencia tienden a crecer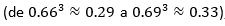 
, mientras que los mínimos de las funciones de no pertenencia tienden a decrecer 
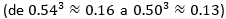. Ello significa que el acceso al examen, en la segunda ronda, les proporcionó a los expertos un nivel mayor de seguridad. Sin embargo, el modelo 3-fuzzy revela que ambos niveles de incertidumbre son superiores al 50 % y apenas disminuyen en menos de una unidad porcentual. Efectivamente:
Esta última observación pone de manifiesto la utilidad de implementar un enfoque (-fuzzy, el cual sirve de modelo para una clase más amplia de respuestas posibles. Finalmente, es importante significar que el cálculo de la distancia 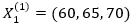expresa una medida del cambio acontecido entre una ronda y otra, pero no bajo la óptica comparativa entre los dominios y las imágenes de ambos números 3-fuzzy triangulares por separado, sino bajo una mirada más omnímoda. El factor 
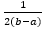de la integral en la Definición 3 elimina la influencia de la longitud del universo X, en el cálculo de la distancia. Además, el valor de distancia calculado 
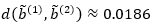representa un 0.93 % de la máxima variación posible pues, como se dijo antes, el valor máximo alcanzable para casos de universo de discurso real y acotado es igual a 2. Si se diseña un Delphi con un número indeterminado de rondas, el hecho de prefijar un valor mínimo para esta distancia puede servir como condición de parada, como se indica en el flujograma de la Fig. 2.
Conclusiones
La presente investigación define estructural y funcionalmente el método Delphi con enfoque (-fuzzy, para el caso específico del pronóstico. Se trata de una generalización de varios enfoques difusos existentes en la literatura, relacionados con estudios prospectivos. Las herramientas matemáticas empleadas sirven para modelar fenómenos reales, tales como respuestas subjetivas aparentemente contradictorias, de carácter más amplio que otros hallazgos descritos bajo los modelos difusos intuicionistas. El ejemplo presentado responde a un suceso real, que si bien no puede ser explicado con efectividad para valores tradicionales del parámetro (, se ajusta a un modelo 3-fuzzy.
Existen también elementos perfectibles, como la necesidad de no excluir respuestas del tipo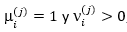 
, las cuales son objetivamente posibles, pero que no se ajustan exactamente al modelo desarrollado. En el ejemplo expuesto, un recurso práctico para sortear esta dificultad puede consistir en asignar un valor < 1, pero suficientemente cercano a la unidad, como valor modal del límite superior en las escalas de las dos últimas preguntas de la Fig. 3. Por otra parte, es necesario valorar en qué medida la adopción del valor ( mínimo es realmente útil en la investigación. En el ejemplo descrito pudo ocurrir que la cantidad de respuestas que conllevaron a tomar 
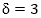fuese muy pequeño respecto a la cantidad de expertos que conforman el panel. En un caso así, el investigador puede valorar si es más viable desechar estas respuestas y adoptar un modelo que responda a la amplia mayoría, como el caso pitagoreano para 
.
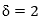Para estudios futuros, resulta interesante valorar la aplicabilidad de otras medidas borrosas de tendencia central. Por ejemplo, las medias geométrica y aritmética (-fuzzy definidas por Jamkhaneh & Garg (2017), las cuales son claramente compatibles con el enfoque adoptado. Asimismo, quedan pendientes problemas relacionados con la ponderación del juicio individual de cada experto, así como la evaluación de respuestas de tipo multicriterio. Todo ello demarca nuevos caminos para dar continuidad al presente trabajo.
