Introducción
El estudio del comportamiento de la precipitación es importante para poder evaluar y predecir las distintas amenazas naturales que tienen como factor común esta variable, la cual en muchas situaciones es el factor desencadenante de desastres como ser inundaciones, sequías, deslizamientos de ladera, entre otros (Romero et al., 2020). Es por ello la importancia de caracterizar la precipitación en términos de sus cantidades, inicio, duración, finalización, así como disponer de información de calidad sobre su intensidad e impactos sobre la zona de estudio. La precipitación incide de manera directa en los distintos procesos que se generan en el sistema climático; y es por ello por lo que existe un consenso sobre la importancia de estudiar su variabilidad espacial y temporal en el marco del cambio climático global.
Honduras es un país que año tras año es afectado por sequias o inundaciones debido a la variabilidad que presenta el régimen pluviométrico en la región, las investigaciones nacionales en el análisis de la precipitación son escasas y debido a esto la necesidad de comprender mejor esta variable meteorológica ha dado origen a este trabajo.
El Distrito Central se ubica en el centro del territorio hondureño, presenta dos estaciones bien definidas: una lluviosa, que inicia en promedio en el mes de mayo y termina en el mes de noviembre, con un descenso en las cantidades de lluvia entre julio y agosto, que se le conoce como canícula; y una seca que se extiende desde el mes de noviembre hasta el mes de abril. Uno de los aspectos relevantes de la importancia de esta investigación es que la economía del país se encuentra basada en la agricultura y los impactos producidos por las inundaciones y sequias a este sector son cuantiosos. Estos términos, inicio y fin de la temporada lluviosa, son tomados en cuenta por los agricultores para calendarizar sus cosechas y optimizar sus producciones (Priyan, 2015).
Realizando análisis estadísticos, es posible establecer un rango de fechas en las cuales se da el inicio de una temporada de lluvia, así como su culminación en la región que se estudie (Alfaro & Hidalgo, 2021), además, es posible determinar la existencia de tendencias de aumento o disminución de la cantidad de lluvia acumulada que pueda presentarse cada cierto tiempo (Paliz et al., 2021).
Materiales y métodos
En este trabajo se analizó la precipitación agrupándola en péntadas, para un intervalo de tiempo de treinta años en el Distrito Central con el fin de identificar el comportamiento del inicio y finalización de la temporada lluviosa, delimitando en el proceso un rango de tiempo en el cual se evidencia el retraso o adelanto del inicio y finalización del periodo de lluvias en el área de estudio, así mismo se utilizó la transformada de Fourier para detectar la presencia de componentes estacionales en la serie temporal de precipitación y tendencias de aumento o disminución en los montos anuales de esta.
Resultados y discusión
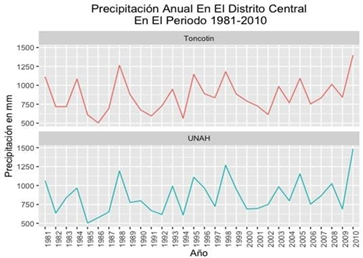
Se analiza el comportamiento de la precipitación anual acumulada durante 30 años abarcando desde 1981 hasta 2010 para las estaciones de Toncontín (Figura 1) y de la Universidad Nacional Autónoma de Honduras (UNAH), cuyas características se describen en la tabla 1.
Tabla 1 - Características de las Estaciones Meteorológicas en el Periodo 1981-2010.
| Periodo | Latitud | Longitud | Altura | ||||||
|---|---|---|---|---|---|---|---|---|---|
| N° | Estación | Años | Grados | Minutos | S” | Grados | Minutos | S” | msnm |
| 1 | Toncontín | 1981-2010 | 14 | 3 | 31 | 87 | 13 | 10 | 1000 |
| 2 | UNAH | 1981-2010 | 14 | 5 | 13 | 87 | 9 | 46 | 1063 |
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 1 - Ubicación de la estación de Toncontín en el aeropuerto de Toncontín (1) y la estación de la UNAH en Ciudad Universitaria (2).
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 2 - Precipitación anual en el Distrito Central para la estación de Toncontín ubicada en el aeropuerto y la estación de la UNAH ubicada en Ciudad Universitaria en el periodo 1981-2010.
Los resultados obtenidos son apreciables en el anexo A en Cuadro 7 que se encuentran expresados visualmente en Figura 2.
Las diferencias que se presentan entre ambas estaciones son debidas a algunos factores como ser la ubicación de las estaciones en el Distrito Central, estas se encuentran a una distancia aproximada de 8 km, las lluvias en la ciudad se deben al ingreso de humedad proveniente de los océanos que rodean al país, en un porcentaje a precipitaciones convectivas, a la humedad proveniente del ingreso de la zona de convergencia intertropical y a la incidencia que tienen los ciclones tropicales y las ondas del este. En promedio para el Distrito Central se determinaron los siguientes valores extremos de precipitación, así como un valor medio durante el intervalo de 30 años seleccionado que pueden observarse en la tabla 2.
Tabla 2 - Valores de Precipitación para el Distrito Central en el Periodo 1981-2010.
| Precipitación Alcanzada | Precipitación en mm |
| Precipitación Máxima | 1441.67 |
| Precipitación Mínima | 539.15 |
| Precipitación Media | 860.95 |
Fuente: Elaboración propia
Un máximo de 1441.67 mm de precipitación para el año más lluvioso y un mínimo de 539.15 mm de lluvia para el año más seco. Además, fueron detectados cuatro años que presentaron valores elevados para cada estación como se muestra en la tabla 3 y en la tabla 4.
Tabla 3 - Precipitación Alta en la Estación de Toncontín en el Periodo 1981-2010.
| Año | Precipitación en mm |
| 1988 | 1264.40 |
| 1995 | 1146.30 |
| 1998 | 1180.00 |
| 2010 | 1399-06 |
Fuente: Elaboración propia
Tabla 4 - Precipitación Alta en la Estación de UNAH en el Periodo 1981-2010.
| Año | Precipitación en mm |
| 1988 | 1193.30 |
| 1995 | 1109.20 |
| 1998 | 1268.50 |
| 2010 | 1484.27 |
Fuente: Elaboración propia
Entre los cuales se encontró un valor máximo de precipitación en el año 2010 para ambas estaciones como es mostrado en la tabla 3 y tabla 4. De estos años, algunos se encentran dentro de la ocurrencia del fenómeno de La Niña, un evento atribuido al enfriamiento del Pacífico más de lo normal y la amplificación de las lluvias, a pesar de que el año 1998 se encuentra dentro de los años del fenómeno de El Niño, tuvo lugar el evento del huracán Mitch (Poveda & Mesa, 1996).
También se encontraron cuatro años con valores bajos de precipitación en la tabla 5 y tabla 6.
Tabla 5 - Precipitación Baja en la Estación de Toncontín en el Periodo 1981-2010.
| Año | Precipitación en mm |
| 1985 | 610.3 |
| 1986 | 503.0 |
| 1991 | 595.4 |
| 1994 | 564.3 |
Fuente: Elaboración propia
Tabla 6 - Precipitación Baja en la Estación de UNAH en el Periodo 1981-2010.
| Año | Precipitación en mm |
| 1985 | 504.5 |
| 1986 | 573.3 |
| 1991 | 668.6 |
| 1994 | 610.8 |
Fuente: Elaboración propia
Con un valor mínimo en el año de 1986 para la estación de Toncontín y en el año de 195 para la estación de la UNAH como se observa en la tabla 5 y tabla 6, respectivamente. En su mayoría, estos años con baja precipitación concuerdan con las manifestaciones del fenómeno de El Niño, adjudicándose al calentamiento del Pacífico y a periodos secos fuertes y prolongados (Poveda & Mesa, 1996).
Luego se procede a visualizar la precipitación de manera mensual para ambas estaciones, apreciándose el comportamiento en la figura 3.
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 3 - Precipitación mensual en el Distrito Central para dos estaciones en el periodo de 1981-2010.
Observando la figura 3 para ambas estaciones presentan los valores más altos de precipitación en los meses de mayo, junio, septiembre y octubre. Además, valores muy bajos de precipitación en los meses de enero, febrero, noviembre y diciembre.
Para ambas estaciones se encontró un valor máximo en el mes de septiembre y un mínimo en el mes de enero de 154.75 mm y 4.52 mm respectivamente para la estación de Toncontín; 162.43 mm y 4.48 mm para la estación de la UNAH. Además, la distribución para ambas estaciones posee un comportamiento bimodal, esto se refiere a los dos puntos con mayor precipitación en los meses de junio y septiembre; y un punto mínimo relativo entre los meses de julio y agosto, el cual es conocido como la canícula, que es el periodo del año donde el calor es más fuerte con una duración alrededor de 40 días (Peralta-Hernández et al., 2008).
Se realizó un estudio de precipitación en el Distrito Central a lo largo de treinta años abarcando desde 1981 hasta 2010. El conjunto de datos de lluvia acumulada al día durante un año se reduce a péntadas (precipitación recolectada durante 5 días), para realizar este proceso no se toma en cuenta el 29 de febrero de los años bisiestos para obtener un total de 73 péntadas por año (Alfaro & Cid, 1999), esto permite tener una cantidad uniforme de datos en todos los años estudiados lo que facilita los cálculos al momento de sacar un promedio de precipitación de la muestra.
Comparando a precipitación de dos años consecutivos en la secuencia de treinta años (por ejemplo: 1981 con 1982, luego 1983 con 1984, etc.) de manera gráfica puede apreciarse en qué péntadas comienza a presentarse una precipitación creciente que es un indico de la temporada lluviosa y los comportamientos decrecientes que muestran las culminaciones de las lluvias.
Guiado del trabajo realizado por (Uriarte, 1981), para cada año se calcula el total de lluvia acumulada y cada péntada se expresa como porcentaje con respecto a la precipitación anual. Para los treinta años se obtiene un promedio para cada péntada, resultando en 73 promedio y se calcula el promedio de todos los datos, lo que se conoce como la gran media, que es el valor representativo si en cada péntada lloviese lo mismo. Lo anterior efectuado para comparar mediante un gráfico el porcentaje que se desvía cada péntada de la gran media, indicando los valores por debajo de esta, ausencias de precipitación y los valores por encima de ella, presencia de lluvias.
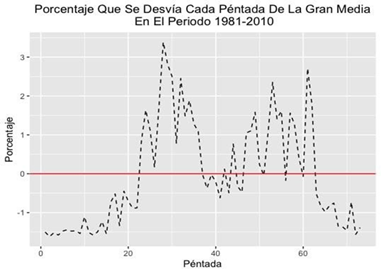
En la figura 4 se representa la diferencia de la gran media con el valor promedio de cada péntada de los 30años. Los intervalos por encima de la línea roja indican periodos con exceso de lluvias y aquellos por debajo muestran periodos deficientes en precipitación.
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 4 - Comparación de cuánto se desvía cada péntada de su valor medio en el periodo de 1981-2010.
Las series temporales se definen como un conjunto de observaciones 𝑦𝑡, cada una registrada en un tiempo específico 𝑡, estas observaciones describen la evolución de un fenómeno o variable a lo largo del tiempo (Brockwell & Davis, 2002). En este caso, la variable a estudiar es la precipitación; y el interés de emplear series de tiempo es analizar los cambios de esta variable con respecto al tiempo y mediante el comportamiento que presente el fenómeno predecir resultados futuros buscando la existencia de estacionalidad de algún evento, es decir, identificar alguna característica que se repita de manera periódica a través del tiempo (Alonso, 2015).
Para el respectivo análisis utilizaremos el proceso de descomposición estacional clásico ETS (Error, Tendencia y Estacionalidad), donde una serie temporal 𝑦𝑡 puede expresarse como la suma de series temporales como se ve en el siguiente modelo aditivo: yt = Tt + St +Rt; donde, 𝑇𝑡 representa la componente de ciclo-tendencia de la serie temporal; 𝑆𝑡 representa la componente de estacionalidad de la serie temporal; 𝑅𝑡 representa la componente de error aleatorio o “ruido blanco” de la serie temporal; 𝑡 ∈ [𝑎. . . 𝑏] tal que 𝑎, 𝑏 ∈ ℤ, donde 𝑡es la representación del tiempo en la serie
Temporal.
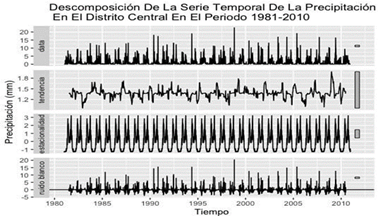
En la figura 5, se muestra cómo se observa la serie temporal 𝑦𝑡 y sus respectivas componentes anteriormente mencionadas, por separado.
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 5 - Descomposición de la serie temporal en sus componentes de tendencia, estacionalidad y ruido blanco en la precipitación por péntadas en el Distrito Central en el periodo de 1981-2010.
Una de las componentes importantes de estudio en las series temporales es la componente de estacionalidad. Esta componente nos ayuda a entender en qué periodos de tiempo suceden variaciones que influyen sobre la serie temporal. Cabe mencionar que la componente de estacionalidad se obtiene dado su unidad de tiempo es una partición de un año (e.g, 73 péntadas existen en un solo año). El estudio de esta componente tiene como motivación el hecho que algunos periodos de tiempo son más importantes en términos de actividad, como es natural preguntarse, en qué periodo de tiempo (¿cada cuántas péntadas?) existe un incremento o decremento en la precipitación a lo largo del tiempo.
La transformada de Fourier se utiliza para descomponer una señal en el dominio del tiempo en todas las frecuencias posibles que la componen, este proceso es reversible, es decir, es posible transformar una serie en el dominio de la frecuencia al dominio del tiempo. Para realizar este procedimiento se hizo uso del lenguaje de programación R, que contiene las herramientas necesarias para computar este algoritmo. La transformada de Fourier comienza con la menor frecuencia posible en este caso, la señal está hecha por 2190 puntos (73 péntadas al año por los 30 años analizados9, entonces la frecuencia más pequeña posible es 2190 = 4.57 × 10−4 𝐻𝑧
La transformada de Fourier comienza con la menor frecuencia posible. En este caso, la señal está hecha por 2190 puntos (73 péntadas al año por los 30 años analizados), entonces la frecuencia más pequeña posible es 2190 = 4.57 × 10−4 𝐻𝑧.
Con esa frecuencia la señal se descompone en un círculo obteniendo todas las medidas en dos dimensiones llamados “vectores” y al sumarlos juntos esto dará la “potencia” final de la frecuencia, lo que ocurre cuando todos los vectores se alinean y apuntan en la misma dirección, creando valores altos que representan la potencia de la frecuencia. Para completar la transformada de Fourier se repite el proceso con diferentes frecuencias hasta calcular toda la potencia de cada posible frecuencia. Cabe resaltar que las frecuencias con valores de potencia más altos representan la mayor periodicidad, de estas, la frecuencia con la potencia más alta expresa la estacionalidad principal de la serie (Anomaly, 2015).
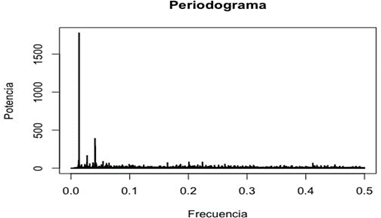 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 6 - Periodo grama de la Serie Temporal de Precipitación en Péntadas en el Distrito Central en el periodo de 1981-2010.
Notemos que en la figura 6 obtenemos dos picos con potencias, uno fuerte, uno débil y luego se va perdiendo a medida que la frecuencia aumenta a valores más altos hasta que tiende a cero, por lo que es señal visual que existen dos periodos de estacionalidad. Para saber cuáles son estos periodos en unidades de péntadas, utilizamos la fórmula 𝑇 = 1, donde 𝑇 es el periodo de tiempo y 𝑓; 𝑓 es la frecuencia a través del análisis de Fourier. Los datos se muestran en la tabla 7.
Tabla 7 - Resultados Obtenidos Utilizando el Algoritmo de la Transformada de Fourier para Detección Específico de Estacionalidad
| Espectro | Frecuencia | Periodo |
|---|---|---|
| 1776.60 | 0.01 | 72.58≈73 |
| 389.22 | 0.04 | 24.46 ≈24 |
Fuente: Elaboración propia
Notemos que, en efecto, se puede apreciar los dos periodos fuertes donde ocurren patrones estacionales, que fueron estimados con anterioridad a través del algoritmo de la transformada de Fourier.
El concepto de tendencia de manera intuitiva nos indica si la serie de tiempo sigue algún patrón (lineal) para indicar cómo podría llegar a comportarse a lo largo del tiempo, es decir, si sigue un patrón monótono ascendente o descendente, pero no ambos. Estudiando la componente de la tendencia nos ayuda a ilustrar y verificar variaciones a lo largo del tiempo y qué fenómenos podrían estar influyendo sobre estas.
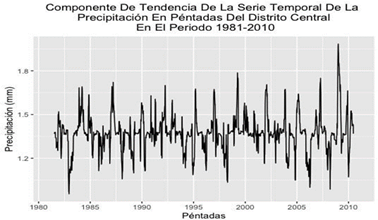 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 8 - Componente de Tendencia de la Serie Temporal de la Precipitación en Péntadas en el Distrito Central en el periodo de 1981-2010.
Notemos que en la figura 8 la componente de tendencia no se logra suavizar de manera clara para encontrar un patrón, esto puede ser a causa del exceso de ruido blanco (error) o la componente estacional puede estar influyendo sobre esta misma, una solución es utilizar un método de “suavizado” con ajuste estacional, es decir, vamos a eliminar los efectos estacionales de la serie de tiempo con el objetivo de analizar la componente de tendencia, ya que se conoce que en algunas estaciones del año esto hace impacto en la precipitación, como por ejemplo, los periodos de lluvia de octubre. Para lograr el ajuste estacional, utilizaremos el algoritmo STL que es el acrónimo de Descomposición Estacional de la Serie Temporal por Suavizado de Diagrama de Dispersión Estimado Localmente (LOESS o Regresión Móvil), entonces la componente de tendencia queda de la siguiente manera:
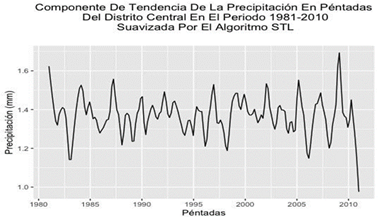 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 9 - Descomposición Estacional de la Serie de Tiempo por Suavizado de Diagrama de Dispersión Estimado Localmente de la Serie Temporal de la Precipitación en Péntadas en el Distrito Central en el periodo de 1981-2010.
Podemos notar en la figura 9 que se observa el patrón de tendencia, aun así, no se aprecia una tendencia monótona lineal.
El Test de Mann-Kendall es utilizado para detectar la existencia de alguna tendencia en la serie de tiempo (Miró et al., 2009). Posee dos ventajas, primero que no es una prueba paramétrica y no requiere que los datos sigan una distribución en particular (en este caso, una distribución gaussiana). Segundo, el test muestra mínima sensibilidad a fuertes interrupciones debido a series temporales que no sean homogéneas. Para este proceso se plantean dos hipótesis: una hipótesis nula 𝐻𝑜 que asume que no hay una tendencia monótona lineal y una hipótesis alternativa 𝐻𝑎 que es la existencia de una tendencia monótona lineal. Al aplicar el test se busca rechazar la hipótesis nula con un valor ?? < 0.05 dado que la significancia a utilizar es de 𝖺= 0.05 (Karmeshu, 2012).
Analizando la figura 8 y figura 9 se sospecha que no hay una tendencia, por lo que se procede a aplicar el test utilizando la siguiente función en el paquete estadístico R (McLeod, 2005).
> 𝑀𝑎𝑛𝑛𝐾𝑒𝑛𝑑𝑎𝑙𝑙 (𝑝𝑒𝑛𝑡𝑎𝑑𝑎. 𝑡𝑠) 𝑡𝑎𝑢 = −11.989, 2 − 𝑠𝑖𝑑𝑒𝑑 𝑝𝑣𝑎𝑙𝑢𝑒 = 0.425
En la primera línea se plantea la función con los datos a tratar y en la segunda nos da los resultados, donde es apreciable un valor 𝑝 = 0.425 el cual no cumple la condición para rechazar la hipótesis nula, lo que indica que no hay una tendencia monótona lineal.
Para determinar el inicio y fin de la temporada lluviosa es necesario tomar en cuenta algunos criterios y trabajar los datos en péntadas. Para aplicar estos criterios hay que tomar en cuenta un valor N que representa el 10% de precipitación acumulada al año dividida por 5 (N/5 mm/día), el cálculo del inicio, fin y duración de la temporada lluviosa se basó en el trabajo de Zambrano, E.; Hernández, F. (Zambrano & Hernández, 2007). Los procedimientos descritos a continuación fueron realizados para dos estaciones ubicadas en el Distrito Central, la estación de Toncontín y la estación de la UNAH, puesto que ambas presentaron información más detallada respecto a datos de precipitación diarios durante una cantidad suficientemente amplia de años, de los cuales se escogieron 30 años abarcando desde 1981 hasta 2010 para realizar el estudio.
Se considera que la estación lluviosa inicia cuando una péntada presenta un valor 𝑁 mm o más de lluvia, al menos una de las dos péntadas siguientes (en orden creciente) también presente un valor de 𝑁 mm o más de lluvia y que las péntadas anterior y posterior a esta última, tengan 0.5 mm de precipitación acumulada. Es decir, 𝑡 = 𝐼𝐸𝐿𝐿 siempre y cuando se cumpla una de las siguientes condiciones:
𝑥𝑡 ≥ 𝑁 𝑚𝑚 𝑦 𝑥𝑡+1 ≥ 𝑁 𝑚𝑚 𝑦 𝑥𝑡+2 > 0.5 𝑚𝑚
(2)
𝑥𝑡 ≥ 𝑁 𝑚𝑚 y 𝑥𝑡+2 ≥ 𝑁 𝑚𝑚 𝑦 𝑥𝑡+1 > 0.5 𝑚𝑚 𝑦 𝑥𝑡+3 > 0.5 𝑚𝑚
(3)
Donde 𝑥𝑡 es el valor de la precipitación acumulada en la péntada 𝑡, con 𝑡 ∈ [1. . .73]. Para ambas estaciones fueron encontrados los siguientes resultados:
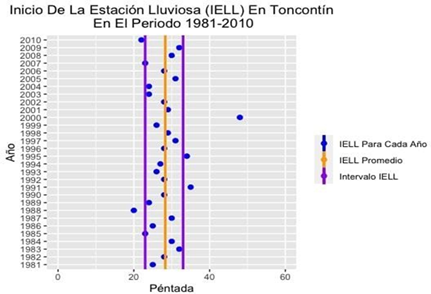 Fuente: Elaboración propia
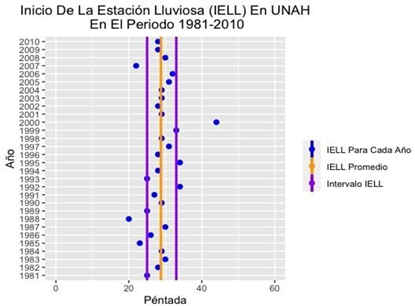
Fuente: Elaboración propiaFig. 10 - IELL para 30 Años con Datos Obtenidos de la Estación de Toncontín en el periodo de 1981-2010.
En la figura 10 se presentan los valores obtenidos para la estación de Toncontín. En color azul, se representan los valores que indican el inicio de la estación lluviosa para cada año. El valor promedio de la péntada que corresponde al IELL, en color naranja que corresponde a 28.3, es decir la péntada 28 más un día (21 de mayo). Y en color morado está expresado el intervalo dentro del cal se encuentra el valor verdadero del IELL que va aproximadamente desde la péntada 23 hasta la 33 (25 de abril al 15 de junio).
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 11 - IELL para 30 Años con los Datos Obtenidos de la Estación de la UNAH en el Periodo de 1981-2010.
De la misma manera que para la estación de Toncontín, en la figura 11 se representan los datos para la estación de la UNAH. En este caso, el valor promedio es 28.8, es decir, 28 péntadas más 4 días (24 de mayo), muy cercano a la péntada 29 con un intervalo aproximado que abarca de la péntada 25 hasta la 33 (5 de mayo al 15 de junio).
Los valores que se presentan fuera del intervalo para ambas estaciones pueden ser causa de las precipitaciones que se producen debido a la ubicación de la estación y en el caso en los cuales estos valores coinciden se debe a un retraso en el inicio de la temporada lluviosa producto de las condiciones atmosféricas de ese periodo de tiempo.
En cuanto a la diferencia de la péntada de IEEL encontrada para cada estación de tres días se relaciona a factores como la distancia a la que se encuentran una de la otra, las corrientes de viento, entre otros, como fue mencionado en las precipitaciones anuales. Sin embargo, la discrepancia de este valor entre ambas estaciones no es significativa puesto que el intervalo superior de la estación de Toncontín se traslapa con el intervalo inferior de la estación de la UNAH, por tanto, las dos presentan un valor aceptable.
Es importante tener en cuenta que 𝑡 no es la misma que en el cálculo de IELL. Para las estaciones se obtuvo lo siguiente:
 Fuente: Elaboración propia
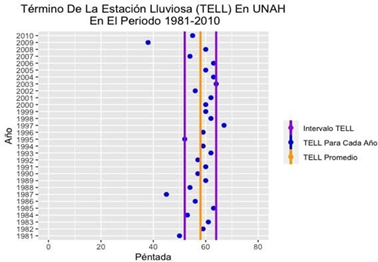
Fuente: Elaboración propiaFig. 12 - TELL para 30 Años con los Datos Obtenidos de la Estación de la Toncontín en el Periodo de 1981-2010.
Para Toncontín, en la figura 12, el valor promedio de TELL se ubica aproximadamente en la péntada 58 (20 de octubre) con un intervalo que se extiende desde la péntada 52 hasta la 64 (20 de septiembre al 20 de noviembre).
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 13 - TELL para 30 Años con los Datos Obtenidos de la Estación de la UNAH en el periodo de 1981-2010.
Para la estación de la UNAH, (Figura 13) se encuentra un valor promedio para TELL ubicado muy próximo a la péntada 58 (20 de octubre) entre las péntadas 52 y 64 (20 de septiembre al 20 de noviembre).
Al igual que para los valores calculados de IELL, los datos encontrados para TELL que están fuera de los intervalos se encuentran afectados por el comportamiento de las precipitaciones locales.
Duración de la Estación Lluviosa (DELL), Para obtener un valor estimado de la duración de la estación lluviosa se realiza un cálculo sencillo el cual consiste en la diferencia de la péntada en que se da el término de la estación lluviosa y la péntada del inicio de la estación lluviosa.
Se observan los siguientes resultados para cada estación en la figura 14 y figura 15.
 Fuente: Elaboración propia
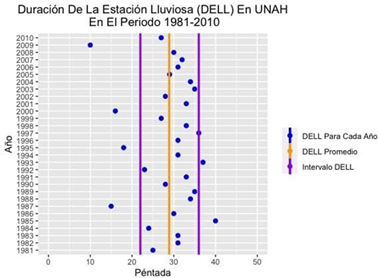
Fuente: Elaboración propiaFig. 14 - DELL para 30 Años con los Datos Obtenidos de la Estación de Toncontín en el Periodo de 1981-2010.
Para Toncontín, en la figura 14, se detectó un DELL promedio correspondiente a 29.9 péntadas (29 péntadas y 4 días) que ronda los 149 días (cercano a los 5 meses), con un margen que abarca alrededor de 21 a 39 péntadas (105 a 195 días), respectivamente.
 Fuente: Elaboración propia
Fuente: Elaboración propiaFig. 15 - DELL para 30 Años con los Datos Obtenidos de la Estación de la UNAH en el Periodo de 1981-2010.
En la estación de la UNAH, figura 15, se encontró un DELL promedio de 28.9 péntadas (28 péntadas y 4 días) que son unos 144 días (4 meses y su tercera semana), con un intervalo que va aproximadamente desde 22 a 36 péntadas (110 a 180 días, respectivamente).
Los valores fuera de los intervalos para ambas estaciones están ligados a las mismas causas de IELL y TELL. La diferencia de los valores presentados por ambas estaciones está relacionado a la discrepancia encontrada en los cálculos para el IELL.
Medias Ponderadas para Cálculo de IELL, TELL y DELL Utilizando Resultados de Ambas Estaciones; para obtener un solo resultado a partir de los valores encontrados para cada estación meteorológica se requiere aplicar la teoría de medias ponderadas, que es utilizada al realizar medidas de cierta cantidad física en distintos laboratorios (en este caso, las dos estaciones). Para realizar este procedimiento se hace uso de las siguientes ecuaciones (Taylor, 1997).
Si tenemos dos mediciones:
𝑚𝑒𝑑𝑖𝑐ión 𝐴: 𝑥 = 𝑥𝐴 ± 𝜎𝐴
(7)
𝑚𝑒𝑑𝑖𝑐ión 𝐵: 𝑥 = 𝑥𝐵 ± 𝜎𝐵
(8)
Donde A y B representan las estaciones meteorológicas, 𝑥𝐴 y 𝑥𝐵 son el valor promedio de la péntada en la que se da el evento para su estación respectiva, 𝜎𝐴 y 𝜎𝐵 son las incertidumbres para cada medición (nos indica el intervalo en el que se encuentra el valor verdadero).
Con los valores de ambas estaciones se determinaron los siguientes resultados:
Tabla 8 - IELL, TELL y DELL en 30 Años para el Distrito Central
| Valor | IELL | TELL | DELL |
|---|---|---|---|
| 𝑋𝑤𝑎𝑣 | 28.5798 | 57.9233 | 29.2818 |
| 𝜎𝑤𝑎𝑣 | 3.3150 | 4.1250 | 5.34414 |
Fuente: Elaboración propia
En la tabla 8 se muestran los valores unificados de ambas estaciones para el Distrito Central, donde
𝑋𝑤𝑎𝑣 representa el valor de la péntada en la que se presenta el inicio de la estación lluviosa (IELL), su término (TELL) y su duración en péntadas (DELL). También se muestran valores de 𝜎𝑤𝑎𝑣 que expresa el margen de error para cada uno de estos índices.
En la precipitación presentada como porcentaje del acumulado anual de lluvias, se encuentras los primeros valores por encima del 0% entre las péntadas 25 y 28 correspondientes a los días 5 y 20 de mayo, respectivamente y entre las péntadas 39 (15 de julio) y 47 (25 de agosto) se expresan valores cercanos y menores al 0% que representan la canícula, con una duración de 40 días. También, entre las péntadas 58 (20 de octubre) y 61 (5 de noviembre) comprenden valores próximos y por debajo del 0%, representando indicios del cese de lluvias.
Se presentan valores mayores en las péntadas 31 y 55, ambas con una magnitud aproximada del 3% de la precipitación anual que corresponden a los días 5 de junio y 5 de octubre, respectivamente, presentan el momento en que hubo mayor cantidad de lluvia acumulada al año. También, en las péntadas 2 y 70 con un valor aproximado del 1.3% por debajo de la media, que se encuentran alrededor de los días del 10 de enero y 20 de diciembre, respectivamente, muestran los días más secos del año. Lo anterior se puede observar en la figura 4.
Sobre el test de Mann Kendall, con un valor 𝑝 = 0.425 no es posible rechazar la hipótesis nula planteada, por lo tanto, no existe una tendencia monótona lineal en la serie de tiempo, esto concuerda con la figura 8 y figura 9, donde no es posible visualizar una tendencia creciente o decreciente.
La sospecha de la existencia de dos periodos estacionales fue confirmada aplicando el algoritmo de la Transformada de Fourier, donde los periodos estacionales se reflejan en las 73 péntadas (el pico con mayor potencia en la figura 7), siendo esta una estacionalidad anual; y cada 24 péntadas (el segundo pico más alto en la figura 7).
Se calcularon los valores para IELL, TELL y DELL para un periodo de 30 años, observándose en el anexo B, en la tabla 11, muestra el valor de la péntada que representa cada índice para la estación de Toncontín y en la tabla 12 se muestran los valores para la estación de la UNAH. Para la estación de Toncontín se encontraron los siguientes valores de péntadas:
𝐼𝐸𝐿𝐿 = 28.3 ± 5.2, 𝑇𝐸𝐿𝐿 = 58 ± 6 y 𝐷𝐸𝐿𝐿 = 29.9 ± 8.5 (alrededor de 150 días, es decir, 5 meses); y para la estación de la UNAH se encontró que 𝐼𝐸𝐿𝐿 = 28.8 ± 4.3, 𝑇𝐸𝐿𝐿 = 58 ± 6 y 𝐷𝐸𝐿𝐿 = 28.9 ± 6.9 (cerca de 145 días).
Con los resultados de la tabla 8, se encontró que la péntada que corresponde al inicio, término y duración de la estación lluviosa corresponden a los siguientes valores: 𝐼𝐸𝐿𝐿 = 29 ± 3, 𝑇𝐸𝐿𝐿 = 58 ± 4, 𝐷𝐸𝐿𝐿 = 29 ± 5.
Conclusiones
El inicio de la temporada lluviosa en el Distrito Central se presenta en promedio en la péntada número 29±3 que corresponde aproximadamente a los días 21 al 25 de mayo, se observó una variación en su inicio a través de los años, mientras que su finalización se presenta en promedio en la péntada 58±4, esto demuestra una variabilidad amplia en el inicio de la temporada lluviosa que genera impactos perjudiciales a los cultivos de los agricultores de subsistencia, los cuales dependen directamente del inicio de las lluvias para iniciar sus siembras. A esta problemática se suma el hecho de que, en esta región de estudio, las cantidades de precipitación anuales históricas son de las más bajas en el territorio hondureño con valores promedio de 860 mm al año y alcanzando valores máximos de 1484.26 mm en el año del 2010 y valores mínimos de 503 mm en 1986, en los periodos de baja precipitación anual se presentan problemas relacionados al acceso del agua por parte de la población en una de las ciudades más grandes del territorio hondureño.
Se confirmo que el régimen pluviométrico del Distrito Central presenta un comportamiento bimodal con máximos en los meses de mayo y septiembre, así mismo la canícula se presenta entre los meses de Julio y agosto. El comportamiento de la precipitación no presenta tendencias monótonas lineales de aumento o disminución en el periodo de tiempo analizado.














