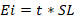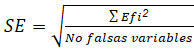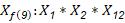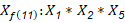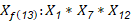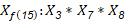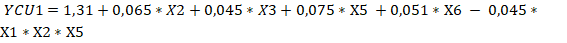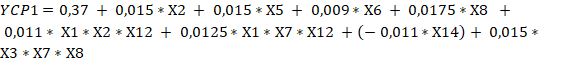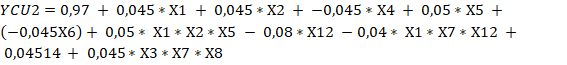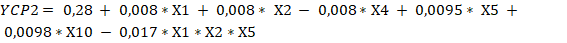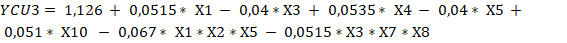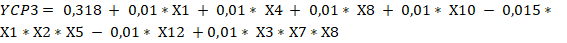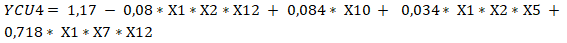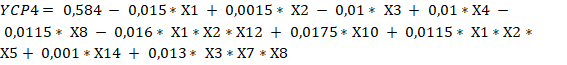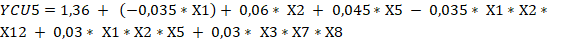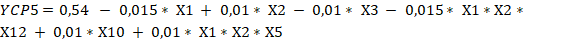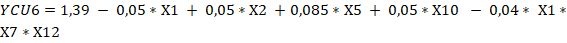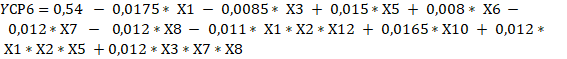Artículo Original

PLANES EXPERIMENTALES PARA MEDIR LA INCIDENCIA DE VARIABLES TECNOLÓGICAS EN LOS INDICADORES DE UNA INVERSIÓN

EXPERIMENTAL PLANS TO MEASURE THE INCIDENCE OF TECHNOLOGICAL VARIABLES IN THE INDICATORS OF AN INVESTMENT

0000-0002-3428-7869Lester A. Alemán Hurtado¹  , 0000-0002-0884-1109Binko Mamady Toure²  , 0000-0003-4232-0646Yoelvis Fleites Avila^{3  *}  , 0000-0003-4363-4401Yailet Albernas Carvajal³  , 0000-0001-5741-8959Erenio González Suárez³ 

¹ Empresa Refinería de Petróleo “Sergio Soto Valdés” de Cabaiguán. Céspedes No. 1 Final, Cabaiguán, Sancti Spíritus, Cuba.

² Departamento de Informática. Universidad de Conakri. República de Guinea.

³ Departamento de Ingeniería Química, Facultad de Química y Farmacia. Universidad Central “Marta Abreu” de Las Villas. Carretera a Camajuaní Km 5 ½. Santa Clara, Villa Clara, Cuba.

RESUMEN

Introducción:

Como la incertidumbre incide en los indicadores económicos de las instalaciones una vez hecha la inversión, se propone cuantificar cada variable tecnológica, con ayuda de diseños experimentales para trabajar en minimizarla.

Objetivo:

Anticipar con rapidez los impactos de la incertidumbre en las variables tecnológicas del diseño de una instalación industrial para definir la estrategia investigativa para introducir la tecnología.

Materiales y Métodos:

Mediante el conocimiento de una tecnología, se realizaron ensayos teóricos para medir la incidencia de las variables del proceso, en indicadores económicos de seis variantes tecnológicas. Debido al alto número de variables independientes se utilizó una combinación de diseños factoriales parciales para medir la sensibilidad de los indicadores a la desviación de las variables.

Resultados y Discusión:

De los resultados de costo por litro de etanol y por peso de producción, se determinaron mediante el diseño de Plackett - Bürman, la significación de los coeficientes de las variables para las seis variantes. Descartando las variables no significativas, y reducidos los diseños a factoriales parciales, se identifica la significación de las variables como medida de la incertidumbre y cuales deben investigarse para resolver los problemas que limitan la introducción de las tecnologías.

Conclusiones:

Aplicando diseños factoriales parciales se definió, con mínimo trabajo experimental, la significación de variables incidentes en los indicadores económicos de las variantes tecnológicas, permitiendo trazar políticas de investigación a fin de minimizar gastos asociados a la tecnología.

Palabras-clave: diseños experimentales; incertidumbre; indicadores económicos; inversión; tecnología

ABSTRACT

Introduction:

As uncertainty affects the facilities economic indicators once the investment has been made, it is proposed to quantify it using experimental designs, in those, each technological variable was minimized.

Objective:

To anticipate quickly the uncertainty impacts in technological variables on an industrial facility design in order to define the research strategy to introduce a technology.

Materials and Methods:

By means of technology knowledge, theoretical tests were carried out to measure the process variables incidence in economic indicators of six technological variants. Due to the high number of independent variables, a combination of partial factorial designs was used to measure the indicators sensitivity to variables deviation.

Results and Discussion:

From the results of cost per liter of ethanol and production weight, the variables coefficients significance for the six variants was determined using the Plackett-Bürman design. Discarding the non-significant variables, and reducing the designs to partial factorials, the variables significance is identified as a measure of uncertainty and which ones should be investigated to solve the problems that limit the introduction of technologies.

Conclusions:

Applying partial factorial designs, the significance of incident variables in the economic indicators for technological variants was defined, with minimal experimental work, allowing the design of research policies in order to minimize expenses associated with technology.

Key words: experimental designs; uncertainty; economic indicators; investment; technology

INTRODUCCIÓN

La meta en el diseño de una instalación industrial es el desarrollo y presentación de una planta completa que pueda operar sobre bases industriales efectivas, esto se logra en los procesos tecnológicos de la industria química sobre la combinación de muchas unidades y partes de equipos dentro de la operación uniforme de una planta, si la planta final es exitosa, cada parte de los equipos deberá de ser capaz de cumplir sus requeridas funciones.

No obstante, muchas veces en los estudios de laboratorio no se pueden resolver problemas sobre el funcionamiento de una planta industrial, por lo que se hace necesario obtener información sobre estos aspectos, esta falta de conocimiento se conoce normalmente como incertidumbre en los datos de diseño (^{González et al., 2021}) y su minimización es una de las tareas fundamentales de las investigaciones actuales en la industria de procesos químicos que requiere minimizar como siempre los costos de producción, los inversionistas, de insumos energéticos y de impactos ambientales negativos.

La aproximación clásica al diseño asume que no existen incertidumbres o variaciones en las corrientes de alimentación, en las temperaturas, en las velocidades de flujo, en las composiciones. Asume que, en los métodos de diseño, las propiedades físicas y los modelos son exactos. Sin embargo, es conocido que existen errores en los datos, errores en los modelos, flujos, temperaturas, concentraciones, etc (^{Lauchy y González, 2005}).

Una vía, científicamente fundamentada, para determinar la sensibilidad de las desviaciones de los efecto de las variables independiente de un proceso tecnológico, son planes experimentales que adecuadamente formulados aseguran la calidad de los resultados y su proyección, (^{Akhnazarova y Kafarov, 1982}) y muestran resultados cercanos a la región del optimo (^{Adler et al., 1975}) esenciales para la optimización del proceso industrial.

Los problemas de incertidumbre inciden esencialmente en la realidad de los indicadores económicos de las instalaciones una vez hecha la inversión. Es por ello que se requiere anticipar con rapidez los impactos de la incertidumbre en las variables tecnológicas del diseño de una instalación industrial para definir la estrategia investigativa y los problemas a resolver para introducir la tecnología siendo este el objetivo de la presente investigación y que es y siempre será de actualidad (^{Miño y González, 2015}).

MATERIALES Y MÉTODOS

Para demostrar las posibilidades de lograr anticipar con tiempo los impactos de la incertidumbre en las variables tecnológicas del diseño de una instalación industrial se utilizó la información disponible de una tecnología desarrollada por el propio equipo de investigación (^{Mesa, 2010}), (^{Mesa et al., 2011a}), (^{Mesa et al., 2011b}), (^{Morales et al., 2011}), (^{Albernas et al., 2012}), (^{Albernas et al., 2014}), (^{Mesa et al., 2016}), (^{Albernas et al., 2017}).

En el trabajo se realizó el cálculo de una planta industrial de etanol de segunda generación a partir de bagazo de caña, considerando una capacidad de 500 hl/día. Este estudio se realizó a partir de trabajos previos donde se definieron las variantes tecnológicas y se precisaron los parámetros esenciales del proceso lo que permitió una vía para desarrollar los balances de masa y energía, el dimensionamiento del equipamiento, así como el cálculo inversionista de dicha planta. Unido a esto se realizó un análisis de sensibilidad a las variables que más incidían sobre los indicadores económicos estudiados (costo unitario y costo por peso). Para ello se realizó un diseño de experimento parcial saturado basado en el método de (^{Plackett y Bürman, 1946}) para definir cuál de las variaciones de las variables era la más significativa y además verificar la existencia los posibles efectos cuadráticos o interacciones entre las mismas utilizando para ello “ensayos de mesa en computadora”.

El propósito fundamental en la aplicación del diseño factorial altamente fraccionado es su capacidad de estudiar todas las variables posibles que afecten el sistema mediante un reducido número de ensayos.

Finalmente, con ayuda de un plan experimental de (^{Box y Hunter, 1961}) se determinaron las interacciones significativas de las variables.

Estos resultados de significación de las variables minimizando el número de experimentos a realizar, al no tenerse que duplicar al ejecutar los referidos al diseño de (^{Plackett y Bürman, 1946}) y poder utilizarlos además como primera réplica del (^{Box y Hunter, 1961}) permitió, al determinar la significación o no de los coeficiente, conocer con rapidez y precisión la sensibilidad de las respuestas estudiadas a la incertidumbre en las variables consideradas y cuantificar su incidencia en el intúbalo de incertidumbre en el caso de ser significativas lo cual era el propósito de la investigación.

2.1 Definición del esquema tecnológico

Según las tecnologías existentes para la obtención de bioetanol, reportadas en la literatura, por diferentes autores y con los estudios reportados por (^{Mesa, 2010}) se llegó a definir un esquema tecnológico.

Este esquema consta de dos etapas de fraccionamiento. En la primera, cuando se obtiene xilosa como producto para la obtención de etanol, la biomasa se somete a la acción de una solución de Ácido Sulfúrico al 1% v/v en presencia de vapor a 120ºC y una relación sólido/líquido de 1:4 kg/l. Cuando la primera etapa está dirigida a la obtención de furfural, la temperatura es 175ºC, la concentración de ácido sulfúrico es 1% en masa en base a la fibra seca y la relación sólido-líquido es 1:1 kg/l. El tiempo de residencia de ambas alternativas es 40 minutos. Posteriormente, el sólido resultante de cada alternativa se trata con una solución de hidróxido de sodio y etanol al 5% masa en base a fibra seca y 30 % v/v respectivamente, también con vapor a 185ºC (^{Mesa et al., 2014}). La relación sólido-líquido es 1:7 y el tiempo de residencia de la segunda etapa de pretratamiento es 60 minutos considerando tiempos de carga y descarga de 20 minutos para cada variante.

Luego de terminado el pretratamiento en dos etapas, la biomasa se somete a la acción de las celulasas por un término de 24 a 36 horas, en el cual se obtiene una solución de azúcares listos para fermentar con levaduras del tipo S. Cerevisiae. Esta operación se puede realizar de tres formas diferentes:

1. Sacarificación y Fermentación Separadas.

2. Presacarificación y Fermentación.

3. Sacarificación y Fermentación Simultáneas.

2.2 Análisis de las diferentes alternativas.

Derivado de este proceso se obtiene un fermento con el grado alcohólico necesario para ser destilado en una columna de destilación.

De lo anteriormente expuesto se derivan seis variantes tecnológicas las cuales se enumeran a continuación:

• Variante 1: Sacarificación y fermentación Separadas con primera etapa a 120ºC.

• Variante 2: Presacarificación y Fermentación con primera etapa a 120ºC.

• Variante 3: Sacarificación y Fermentación Simultáneas con primera etapa a 120ºC.

• Variante 4: Sacarificación y fermentación Separadas con primera etapa a 175ºC.

• Variante 5: Presacarificación y Fermentación con primera etapa a 175ºC.

• Variante 6: Sacarificación y Fermentación Simultáneas con primera etapa a 175ºC.

Las temperaturas de la primera etapa definen si el coproducto es Furfural (^{Morales et al., 2011}), (^{Mesa et al., 2014}) o Xilitol que es además un producto de gran interés (^{Rabassa et al., 2015}).

2.3 Definición de las bases y ecuaciones para el diseño de los equipos

De acuerdo a las características peculiares de cada etapa básica, la producción de bioetanol y sus coproductos, se llevarán a cabo en una planta de forma semicontinuo. Capacidad de producción de 500 hl de etanol diario, se operará 24 horas al día, durante 300 días al año.

Para cada una de las seis variantes tecnológicas se calcularon los balances de materiales y energía y se seleccionó el equipamiento adecuado según ^{Mesa, (2010}).

El dimensionamiento de los equipos se realizó tomando como base las ecuaciones de diseño de cada uno de ellos reflejado en la literatura (^{Lauchy y González, 2005}).

Con los estimados de costo reportados por (^{Peters y Timmerhaus, 1991}) y los resultados del diseño y del balance de materiales se calcularon los costos inversionistas y los costos totales de producción.

Sin embargo, este resultado puede conducir a un análisis incompleto sobre cuál de las variaciones de las variables son las más significativas, ya que no se tiene en cuenta la combinación de dos o más de ellas al mismo tiempo, sus interacciones ni sus posibles efectos cuadráticos.

Es por ello que se propuso un estudio de sensibilidad utilizando para este propósito un diseño fraccional saturado como el de (^{Plackett y Bürman, 1946}) que puede resolver este problema con un mínimo de trabajo “experimental de mesa”.

Para el estudio se propuso un diseño de 11 variables reales y 4 falsas variables. Conformando una matriz de 15 variables, con 16 experimentos. El Plan Experimental a ejecutar para cada una de las variantes tecnológicas se muestra en la Tabla 1.

Tabla 1 Matriz del plan experimental de Plackett - Bürman para 11 variables (Factores) 

No.	X1	X2	X3	X4	X5	X6	X7	X8	Xf	X10	Xf	X12	Xf	X14	Xf
1	1	1	1	1	-1	1	-1	1	1	-1	-1	1	-1	-1	-1
2	1	1	1	-1	1	-1	1	1	-1	-1	1	-1	-1	-1	1
3	1	1	-1	1	-1	1	1	-1	-1	1	-1	-1	-1	1	1
4	1	-1	1	-1	1	1	-1	-1	1	-1	-1	-1	1	1	1
5	-1	1	-1	1	1	-1	-1	1	-1	-1	-1	1	1	1	1
6	1	-1	1	1	-1	-1	1	-1	-1	-1	1	1	1	1	-1
7	-1	1	1	-1	-1	1	-1	-1	-1	1	1	1	1	-1	1
8	1	1	-1	-1	1	-1	-1	-1	1	1	1	1	-1	1	-1
9	1	-1	-1	1	-1	-1	-1	1	1	1	1	-1	1	-1	1
10	-1	-1	1	-1	-1	-1	1	1	1	1	-1	1	-1	1	1
11	-1	1	-1	-1	-1	1	1	1	1	-1	1	-1	1	1	-1
12	1	-1	-1	-1	1	1	1	1	-1	1	-1	1	1	-1	-1
13	-1	-1	-1	1	1	1	1	-1	1	-1	1	1	-1	-1	1
14	-1	-1	1	1	1	1	-1	1	-1	1	1	-1	-1	1	-1
15	-1	1	1	1	1	-1	1	-1	1	1	-1	-1	1	-1	-1
16	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1

Las variables consideradas según la experiencia del grupo investigador fueron:

Variables independientes

X1: Precio bagazo ($/kg); X2: Precio enzimas ($/kg); X3: Precio vapor ($/t)

X4: Precio Hidróxido de Sodio ($/t); X5: Cantidad de enzimas (kg); X6: Hidromódulo segunda etapa; X7: % De Etanol segunda etapa; X8: % Hidróxido de Sodio segunda etapa; X10: Capital Fijo Invertido ($); X12: Capacidad instalada de etanol y con ello de coproducto (hl/día); X14: Producción de coproducto (Xilosa o Furfural) (t/día)

Con rangos de variación estudiados por ^{Mesa (2010}) y recomendadas de oportunidades de mercado (^{Rabassa et al., 2015}).

Siendo: X9, X11, X13 y X15 falsas variables o posibles interacciones

Y los parámetros de respuesta:

• Y₁: CU: el costo unitario en pesos por litro de etanol producido

• Y₂: CP: el costo en peso de cada peso producido

Aquí no es necesario hacer réplicas para establecer las varianzas y los errores estándares con vistas a determinar la significación de los coeficientes pues eso se logra a través del valor de los coeficientes de las falsas variables (^{Isaccson, 1970}), (^{González et al., 2021}) mediante la expresión 1:

() 1

En la cual t, es la t de Student tabulada para un número de grados de libertad igual a la cantidad de falsas variables (nf) y el Error Estándar, SE, se determina de la expresión 2:

() 2

Lo que permite fijar la significación de las variables independientes en los parámetros de respuesta y proponer decisiones sin repetir ensayos y minimizar la incertidumbre.

Al descartar variables es posible recomendar la reducción del diseño de Plackett -Bürman a uno de (^{Box y Hunter, 1961}) lo que se ha hecho para experimentos de laboratorio, (^{González et al., 2021}) y tasar qué aspectos interactúan en las variaciones de los indicadores económicos. Para valorar el posible efecto de las interacciones se consideró las relaciones generadas para un diseño factorial parcial de (Box y Hunter, 1961) que para el diseño se muestran en las expresiones 3, 4, 5 y 6.

() 3

() 4

() 5

() 6

RESULTADOS Y DISCUSIÓN

Una vez realizados los cálculos pertinentes para cada una de las combinaciones de las variables se obtuvieron los resultados para cada ensayo de la matriz de diseño del Plan Experimental que se presentan en la Tabla 2 para las seis variantes tecnológicas.

Tabla 2 Resultados de los cálculos del efecto de los factores, en el experimento teórico, en los parámetros de respuesta de costo unitario (CU) y costo por peso (CP) en cada ensayo y variante tecnológica 

No.	VAR 1		VAR 2		VAR 3		VAR 4		VAR 5		VAR 6
	CU	CP	CU	CP	CU	CP	CU	CP	CU	CP	CU	CP
1	1,35	0,38	0,889	0,259	0,989	0,28	1,41	0,56	1,24	0,51	1,28	0,52
2	1,45	0,34	1,450	0,344	1,45	0,34	0,72	0,48	1,33	0,46	1,32	0,45
3	1,34	0,38	0,920	0,267	1,07	0,31	0,78	0,43	1,43	0,56	1,35	0,54
4	1,42	0,40	1,020	0,294	1,14	0,33	0,80	0,60	1,29	0,52	1,44	0,56
5	1,24	0,35	0,840	0,2462	1,06	0,30	1,54	0,58	1,37	0,54	1,44	0,56
6	1,18	0,34	0,839	0,246	0,97	0,28	1,44	0,56	1,22	0,51	1,13	0,48
7	1,21	0,35	0,839	0,246	1,06	0,30	1,51	0,58	1,35	0,54	1,35	0,54
8	1,52	0,43	1,140	0,326	1,36	0,38	1,82	0,65	1,61	0,60	1,65	0,61
9	1,21	0,35	1,020	0,294	1,10	0,32	0,78	0,59	1,22	0,50	1,29	0,52
10	1,21	0,35	0,889	0,259	1,06	0,30	1,48	0,57	1,27	0,52	1,24	0,51
11	1,41	0,40	1,019	0,294	1,21	0,35	0,83	0,61	1,53	0,57	1,50	0,57
12	1,20	0,34	0,839	0,246	0,95	0,27	1,34	0,53	1,29	0,51	1,24	0,51
13	1,26	0,36	0,839	0,246	1,07	0,31	1,63	0,60	1,40	0,55	1,46	0,56
14	1,50	0,42	1,020	0,294	1,19	0,34	0,85	0,62	1,44	0,56	1,60	0,60
15	1,56	0,44	1,012	0,294	1,25	0,35	0,89	0,64	1,55	0,58	1,64	0,61
16	1,02	0,29	0,920	0,267	1,12	0,32	0,79	0,59	1,32	0,53	1,31	0,53

Los coeficientes de las variables se hallaron según ^{Isaccson, (1970}) como sigue en la Tabla 3 y Tabla 4.

Tabla 3 Estimados de los coeficientes de las variables para el método de Plackett- Bürman para los casos en los cuales la primera etapa es a 120 ^oC 

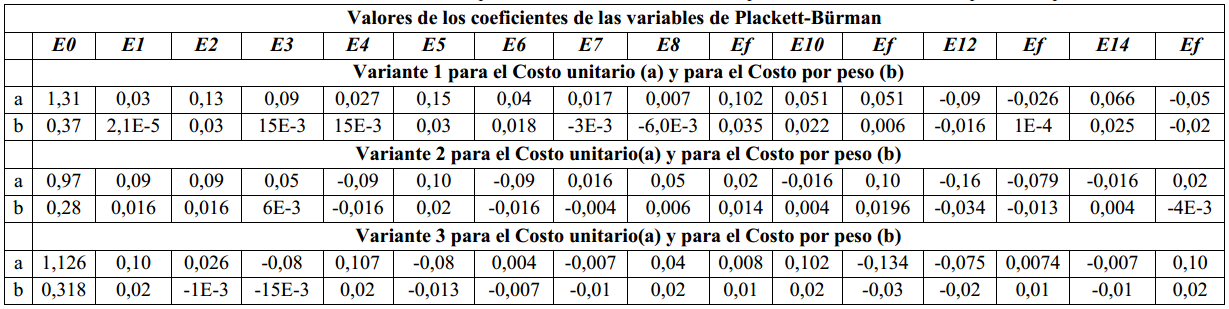
Tabla 4 Estimados de los coeficientes de las variables para el método de Plackett- Bürman para los casos en los cuales la primera etapa es a 175 ^oC 

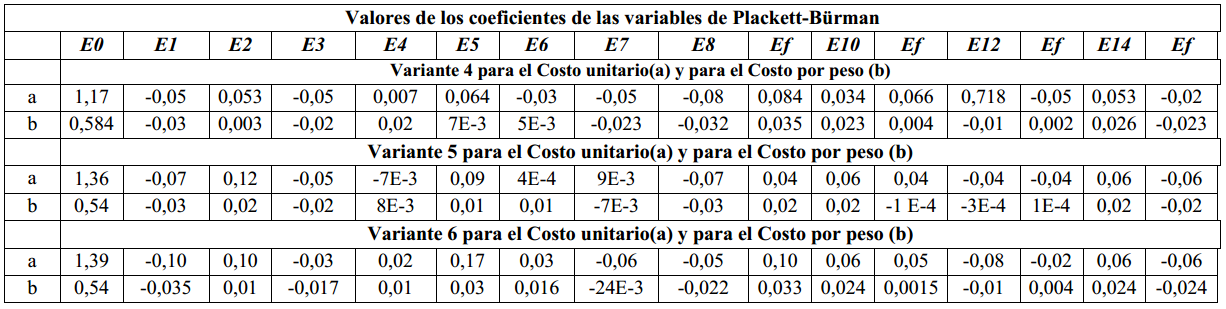
De estos resultados considerando los valores de las falsas variables se encontró para cada experimento los Errores Estándar (EE) y de allí considerando los valores de la t de Student de interés en el estudio (^{Adler et al., 1975}) de determinaron los intervalos de significación como se resume en la Tabla 5 Aquí se tuvo en consideración la recomendación de ^{Isaccson, (1970}), cuando se utiliza el método de Plackett- Bürman cuando se trabaja con datos industriales de estimar la t de Student con una probabilidad del 85 % y cuatro grados de libertad, es decir: 1,19.

Tabla 5 Intervalos de significación de los estimados mediante el método de Plackett- Bürman para el caso en el cual la primera etapa es a 120 ^oC y 170 ^oC 

∆Ei	VAR 1	VAR 2	VAR 3	VAR 4	VAR 5	VAR 6
CU	0,0760	0,0792	0,0798	0,0711	0,0523	0,0733
CP	0,0154	0,0163	0,0169	0,0161	0,0158	0,0166

Un análisis de los resultados de significación de las variables permite concluir que todas las funciones de respuestas de las seis alternativas tienen que considerar interacciones, ajustándose a diseños factoriales parciales del tipo (^{Box y Hunter, 1961}), pero considerando diferentes cantidades de variables independientes, por lo tanto, y de acuerdo con los contrastes tomados para definir las falsas variables y la forma de determinar el valor de los coeficientes para un diseño factorial fraccionado las ecuaciones 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 y 18 evidencian los resultados.

() 7

() 8

() 9

() 10

() 11

() 12

() 13

() 14

() 15

() 16

() 17

() 18

Siendo significativo que tanto los costos unitarios de producción de etanol como los por peso de valor producido, en el caso que se utiliza como temperatura de la hidrólisis ácida 120ºC y cuando se utiliza 170ºC el efecto de las diferentes variables independientes no se manifiesta por igual en todas las alternativas o variantes. Para su estudio deben considerarse los aspectos generales y los de interés por cada alternativa lo que es factible a partir de los resultados obtenidos al aplicar el diseño factorial de experimentos para determinar el impacto de cada uno de los factores sobre los indicadores económicos.

Para el precio o costo del bagazo (X1)

Se encontró que el precio del bagazo incide significativamente en todas las alternativas de forma directa o en interacción con otras variables en indicadores seleccionados para cualquiera de las variantes tecnológicas por lo que se requiere profundizar de inmediato en las vías para disminuirlo.

Para el precio de las enzimas (X2)

El efecto del precio de las enzimas es significativo por si solo con alto nivel de trascendencia, siéndolo también en algunos casos con sus interacciones y de forma perjudicial a los indicadores por lo que se debe trabajar en minimizar los precios de las enzimas.

Para el precio del vapor (X3)

El impacto no es tan alto como en el caso de las enzimas pues solo aparece significativo por si solo en las últimas alternativas vinculadas al uso de altas temperatura en la hidrólisis ácida y en forma de interacciones, lo que indica que para introducir las variantes tecnológicas que incluyen la producción de Furfural se debe minimizar los costos del vapor.

Para el precio del Hidróxido de Sodio (X4)

El comportamiento para las primeras variantes tecnológicas si es significativo el efecto del precio del Hidróxido de Sodio con alto nivel de significación mientras que en las otras variantes, no lo es siempre con alto nivel de significación, lo que indica que no es un aspecto a priorizar minimizar los costos del Hidróxido de Sodio.

Para la cantidad de enzimas (X5)

El comportamiento requiere trabajar en disminuir las cantidades de enzimas a utilizar explorando en el reciclado de este producto.

Para el Hidromódulo de la segunda etapa (X6)

La incidencia del hidromódulo en la segunda etapa es también solo apreciable para las dos primeras variantes tecnológicas y en los costos por peso de la variante número 6 por lo que trabajar en esta dirección no es de prioridad inmediata.

Para el % de etanol de la segunda etapa (X7)

El comportamiento es similar al caso de la variable anterior con significación limitada.

Para el % de Hidróxido de Sodio de la segunda etapa (X8)

En este caso el nivel de significación es muy bajo presente solamente con una probabilidad por lo que prácticamente puede dejar de considerarse en todas las variantes tecnológicas.

Para el Capital Fijo Invertido (X10)

El Capital Fijo Invertido (X10) es una variable frecuentemente significativa en el rango estudiado. La misma es de vital importancia al ser esta función del costo de los equipos y de su capacidad, por lo que debe trabajarse en la secuencia de la estrategia inversionista para recuperar los valores invertidos.

Capacidad instalada de etanol y con ello de coproducto (X12)

El incremento de la capacidad instalada, como era de esperar, incide positivamente en los indicadores económicos de la mayoría de las alternativas de forma directa o en las interacciones por lo que debe trabajarse en posibilitar el uso de la mayor capacidad posible de materias primas para utilizar las más altas capacidades de producción.

Producción de coproducto (Xilosa o Furfural) (X14)

La alternativa tecnológica a utilizar no incide en general en los indicadores económicos por lo que una u otra producción podrá acoplarse a las instalaciones que utilicen la hidrólisis ácida, lo que permite mayores respuestas al mercado y más flexibilidad en los análisis inversionistas (^{Rabassa et al., 2015}).

Aquí queda demostrado que elementos desarrollados en esta investigación pueden anticipar los impactos de la variable tecnológicas en el diseño de equipos de forma más rápida que la forma tradicional aplicada hasta el momento.

CONCLUSIONES

1. Con el uso del método de Plackett-Bürman se pueden definir la significación de la variación de las variables que más inciden en los indicadores económicos de las variantes tecnológicas, lo que demuestra las potencialidades del método para trazar políticas de investigación con el objetivo de minimizar los gastos inversionistas en una nueva tecnología.

2. En las variables estudiadas no existen influencias cuadráticas, pero sí interacciones entre las mismas, lo cual está demostrado por la significación de las falsas variables incluidas en la matriz de diseño y el procedimiento aplicado.

3. La combinación del uso de un diseño factorial parcial con los mismos experimentos permite valorar el efecto de las interacciones de las variables en los indicadores económicos, lo cual posibilita trazar una estrategia en las inversiones pues son significativas las valoraciones extremas de una variable en presencia de valores máximos o mínimos de otras.

4. El análisis de sensibilidad de las diferentes variables demostró que no son de interés en el estudio todas las variables incluidas inicialmente por lo que solo debe considerarse un grupo de ellas en cada variable seleccionada, lo cual dependerá de las demandas del mercado.

5. Resalta de los resultados la importancia la investigación en la anticipación de la influencia de la variabilidad en las decisiones del diseño del proceso e inversionista.

REFERENCIAS

Adler, Y., Markova, E.V., & Granovsky, Y.V., The Design of Experiments to find optimal conditions., Editorial MIR, Moscow, 1975, pp. 1- 287.

Akhnazarova, S., & Kafarov, V., Experiment optimization in chemistry and chemical Engineering., Editorial MIR, Moscow ,1982, pp. 1-312.

Albernas, Y., Corsano, G., González, M., Verelst, H., & González, E., Metodología para la síntesis y diseño óptimo de plantas discontinuas., Afinidad, Vol. 69, No. 560, 2012, pp. 295-300.

Albernas, Y., Corsano, G., Morales, M., González, M., Santos, R., & González, E., Optimal design for an ethanol plant combining first and second-generation technologies., CT&F - Ciencia, Tecnología y Futuro, Vol. 5, No. 5, 2014, pp. 97-120.

Albernas, Y., Corsano, G., González, M., & González, E., Preliminary design for simultaneous saccharification and fermentation stages for ethanol production from sugar cane bagasse., Chemical Engineering Research and Design, Vol. 126, 2017, pp. 232-240.

Box, G.E.P., & Hunter, J.S., The 2^k-p fractional, Factorial Designs., Technometrics, Vol. 3, No. 3, 1961, pp. 311-351.

Lauchy, A., & González, E., Vías para el diseño de nuevas instalaciones de la industria química, fermentativa y farmacéutica., Capítulo 5: Incertidumbre económica en las inversiones de plantas de la industria química, Editorial Científico Técnica, La Habana, Cuba, 2005, pp. 223-243.

González, E., Concepción, D.N., Miño, J.E., Pérez, A., & Cerda, V., Gestión del conocimiento en la industria de procesos con apoyo de herramientas matemáticas., Editorial Samuel Feijóo, Universidad Central “Marta Abreu” de Las Villas, Cuba, 2021, pp. 1-196.

Isaccson, W.B., Statistical Analyses for Multivariable Systems, Chem Eng., Vol. 6, 1970, pp. 69-75.

Mesa, L., Estrategia investigativa para la tecnología de obtención de etanol y coproductos del bagazo de la caña de azúcar., Tesis presentada en opción al Grado Científico de Doctor en Ciencias Técnicas, Especialidad Ingeniería Química en la Universidad Central “Marta Abreu” de Las Villas, Cuba, 2010.

Mesa, L., González, E., Cara, C., González, M., Castro, E., & Mussatto, S.I., The effect of organosolv pretreatment variables on enzymatic hydrolysis of sugar cane bagasse., Chemical Engineering Journal, Vol. 168, 2011a, pp. 1157-1162.

Mesa, L., Gonzalez, E., Romero, I., Ruiz, E., Cara, C., & Castro, E., Comparison of process configurations for ethanol production from two-step pretreated sugarcane bagasse., Chemical Engineering Journal, Vol. 175, 2011b, pp. 185-191.

Mesa, L., Morales, M., Gonzalez, E., Cara, C., Romero, I., Castro, E., & Mussatto, S., Restructuring the processes for furfural and xylose production from sugarcane bagasse in a biorefinery concept for ethanol production., Chemical Engineering and Processing, Vol. 85, 2014, pp. 196-202.

Mesa, L., Albernas, Y., Morales, M., Corsano, G., & González, E., Integration of organosolv process for biomass pretreatment in a Biorefinery., in: Biomass fractionation technologies for a lignocellulosic feedstock based biorefinery, Elsevier, 2016, pp. 229-254.

Miño, J.E., & González, E., Acciones para la correcta terminación y valoración de resultados en la industria química y fermentativa., Editorial Universitaria, Universidad Nacional de Misiones, Posadas, Argentina, 2015, pp. 61-88.

Morales, M., Espino, I., Mesa, L., Acosta, D., González, E., & Castro, E., Evaluación de residuales de la hidrólisis ácida del bagazo como productos de alto valor agregado., Afinidad, Vol. LXVIII, No. 555, 2011, pp. 1-6.

Peters, M.S., & Timmerhaus, K.D., Plant design and economics for Chemical Engineers., McGraw Hiill International Edition, 1991, pp. 1-897.

Plackett, R.L., & Bürman, J.P., The design of optimun multifactorial experiments., Biometrika, Vol. 33, 1946, pp. 305-325.

Rabassa, G., González, E., Pérez, A., Miño, J.E., & Pérez, A., D-Xilosa y Glucosa a partir de residuos de la Industria Azucarera., Revista Científica de la UCSA, Vol. 2. No. 2 2015, pp. 6-22.

Recibido: 01 de Febrero de 2021; Revisado: 20 de Febrero de 2021; Aprobado: 26 de Marzo de 2021

^* Autor para la correspondencia: Yoelvis Fleites, Email:[e-mail]

Los autores declaran que no existen conflictos de interés.

M.Sc. Lester A. Alemán Hurtado. Contribuyó a la concepción de la investigación.

Dr.C. Binko Mamady Toure. Contribuyó a la concepción de la investigación y realizó parte de los cálculos del diseño experimental.

Ing. Yoelvis Fleites Avila. Realizó parte de los cálculos del diseño experimental.

Dra.C. Yailet Albernas Carvajal. Contribuyó con la estimación de los valores inversionistas y de los costos de producción.

Dr.Sc. Erenio González Suárez. Contribuyó a la concepción de la investigación y realizó el diseño del plan experimental.