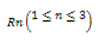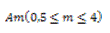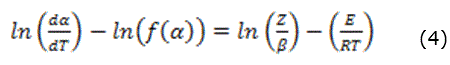ARTICULOS

 

Cinética de la pirólisis de residuos madereros ecuatorianos

 

Kinetic of ecuadorian wood residues pyrolysis

 

 

Ms. C. Manuel Angel Cantos-Macías^I, Dra. C. Omaida Quesada-González^II, Lic. Alejandro Ross-Mesa^II, Dr. C. Angel Luis Brito-Soubanell^III, Lic. Abdel Casanova-Gómez^IV

 

^IUniversidad Técnica de Manabí, Ecuador
^IIFacultad de Ciencias Naturales y Exactas. Universidad de Oriente, Cuba, [e-mail]
^IIIFacultad de Ingeniería Mecánica e Industrial. Centro de Energía y Refrigeración, Universidad de Oriente, Cuba
^IVCentro de Investigaciones para la Industria Minero Metalúrgica, La Habana, Cuba

 

 

---

RESUMEN

El uso de los alimentos como fuente de energía ha sido muy cuestionado y en este sentido, los residuos agroforestales muestran potencialidades. El objetivo del trabajo es caracterizar química y energéticamente estos residuos procedentes del Ecuador y estudiar la cinética de su pirolisis, como alternativa para su aprovechamiento. Se realizó análisis elemental, inmediato y se aplican técnicas de análisis térmico. El mayor contenido de carbón y menor humedad y cenizas de teca, favorecen su aprovechamiento energético, con respecto a Fernán Sánchez. Sus contenidos de nitrógeno y azufre inferiores al 1 % garantizan bajas emisiones de NO_x y SO₂ reduciendo su impacto ambiental. El uso combinado de ATG, TGD y CDB permiten identificar las tres etapas del craqueo pirolítico, la descomposición de hemicelulosa, celulosa y lignina respectivamente. Su estudio cinético demostró que la primera y tercera etapas están determinadas por procesos difusivos fundamentalmente y en la segunda prevalecen diferentes modelos cinéticos.

Palabras clave: residuos madereros, pirólisis, cinética, teca, Fernán Sánchez.

---

ABSTRACT

The use of food as a source of energy has been questioned and agroforestry waste shows potential for these purposes. The objective of the work is to realize the chemical and energetic characterization of waste from Ecuador and study the kinetics of its pyrolysis, as an alternative for its use. Elemental, immediate analysis was carried out and thermal analysis techniques were applied. The higher carbon content and lower humidity and ash of Teak, favor its energétic use, with respect to Fernán Sánchez. In addition, its nitrogen and sulfur contents below 1 %, guarantee low NO_x and SO₂ emissions, reducing its environmental impact. The combined use of TGA, DTG and DSC allows to identify the three stages of pyrolytic cracking, the decomposition of hemicellulose, cellulose and lignin. His kinetic study showed that the first and third stages are determined by diffusive processes fundamentally and in the second, different kinetic models prevail.

Keywords: wood residues, pyrolysis, kinetic, teka, Fernán Sánchez.

---

 

 

INTRODUCCIÓN

Las reservas de combustibles fósiles son finitas y su utilización para la generación de energía ha contribuido al aumento de emisiones gaseosas, que contaminan el medio ambiente e incrementan el calentamiento de la atmósfera terrestre. Además, su regeneración es mucho más lenta que la velocidad con que se consumen éstos, viéndose así afectado el ciclo del carbono [1]. La utilización de tecnologías de energías renovables como la eólica, geotérmica, hidráulica, solar y la obtenida a partir de la biomasa, se presentan como alternativas en el mediano y largo plazo para el reemplazo parcial de estos combustibles fósiles [2]. Esta última resulta centro de atención en esta investigación.

La biomasa es toda la materia que se puede derivar directa o indirectamente de la fotosíntesis de las plantas, es decir es energía solar transformada. La misma para fines energéticos, puede provenir de fuentes como las plantaciones perennes, las herbáceas de cosecha anual, las gramíneas y las oleaginosas, entre otras. También se obtiene de los residuos de la agricultura, de la industria procesadora de alimentos, de la manufacturera de productos de madera y de los residuos sólidos industriales o urbanos. Actualmente se estima que los combustibles obtenidos a partir de biomasa, hacen una contribución cercana al 10 %, al suministro primario de energía en el mundo [3].

La ciencia actual centra su atención en el tratamiento de residuales. La realidad es que, durante el aprovechamiento de las maderas para la actividad humana, se generan grandes cantidades de residuos sólidos. En Ecuador, desde el año 2005 hasta el 2015, como resultado de un programa de reforestación de árboles de rápido crecimiento y explotación, han sido sembradas 404,10 ha de Fernán Sánchez (Triplaris guayaquilensis) lo que equivale a 161 640 árboles y 8 994 ha de teca (Tectona grandis) equivalentes a 3 238 408 árboles [4].

Los procesos fundamentales de transformación de la biomasa se concentran en tres grupos: combustión directa, los bioquímicos y los termoquímicos. Los procesos de transformación termoquímica son la pirólisis, la gasificación y la combustión. A través de estos procesos se producen diferentes fracciones de combustibles sólidos, líquidos y gaseosos y energía térmica. La fracción en masa de cada uno de estos productos puede ser influenciada por medio de la variación de los parámetros del proceso. El presente trabajo se enfoca especialmente en el proceso de pirólisis.

La pirólisis es la degradación térmica o volatilización de la biomasa en ausencia de oxígeno. A través de la variación de los parámetros del proceso de pirólisis como: tipo de biomasa, temperatura máxima, condiciones de la atmósfera de reacción, velocidad de calentamiento y el tiempo de permanencia de los productos en el reactor, es posible influir en la distribución y características de sus principales productos. El material sólido o carbonizado obtenido se puede utilizar como combustible en procesos industriales, en la cocción de alimentos o como materia prima para la producción de carbón activado. El gas producido se utiliza para la generación de energía mecánica y térmica o puede ser transformado en otros productos químicos. El producto líquido, también identificado como condensado o bioaceite, puede ser convertido en un combustible rico en hidrocarburos para su combustión en motores y en la generación de energía mecánica y térmica [3].

Cada tipo de biomasa exhibe un comportamiento particular en cuanto a las características de los productos obtenidos, bajo determinadas condiciones de operación; siendo fundamental el conocimiento del comportamiento cinético del material, para el desarrollo de sistemas de conversión tecno-económicos factibles, mediante procesos de termodescomposición [5]. El análisis termogravimétrico es la técnica más utilizada para el análisis cinético de los procesos termoquímicos y este análisis es indispensable para el diseño, escalado, operación y viabilidad de sistemas de conversión de biomasa a nivel industrial. Es por ello que este trabajo tiene como objetivo caracterizar química, energética y estructuralmente algunos residuos forestales del Ecuador, procedentes de las maderas teca y Fernán Sánchez y abordar un estudio de la cinética de su pirólisis, con la finalidad futura de obtener carbón vegetal.

 

FUNDAMENTACIÓN TEÓRICA

Para estudiar la velocidad de una reacción heterogénea, cuando se emplean métodos no isotérmicos, la expresión básica que define este parámetro es:

Este modelo describe la dependencia de la velocidad de reacción con el grado de avance (a) de la reacción (tabla 1) [6].

En cinética de sistemas heterogéneos, la validez de la ecuación de Arrhenius está asociada a la interpretación física que se les atribuya a los valores experimentales de la energía de activación y el factor pre-exponencial. La primera está directamente relacionada con la entalpía de activación y el segundo con la frecuencia de vibración de los átomos en la red cristalina [7].

TABLA 1. FUNCIONES DIFERENCIALES f(α) E INTEGRALES g(α) MÁS COMUNES UTILIZADAS EN EL MÉTODO DE AJUSTE DE MODELO [6]

Modelo	Símbolo	.f(a)	.g(a)
Difusión unidimensional	D1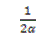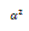
Difusión bidimensional	D2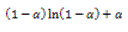
Difusión tridimensional (Jander)	D3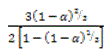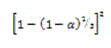
Difusión tridimensional (Ginstring-Brounshtein)	D4
Crecimiento unimolecular	F1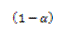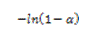
Fase de frontera controlada
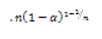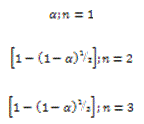Nucleación y crecimiento (Avrami-Eroteev)

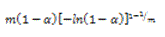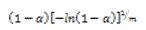Para el estudio de la cinética de estas reacciones a partir de técnicas de análisis térmico, pueden utilizarse el método de ajuste de las funciones con sus diversas expresiones diferenciales o integrales o los métodos de isoconversión o de cinética libre.

Método de ajuste de las funciones

De forma general, el método se basa en el ajuste por correlación estadística de una serie de modelos matemáticos (diferenciales o integrales) que describen la cinética de una reacción heterogénea [7]. Para el estudio cinético se tomaron las ecuaciones de Coats-Redfern (método integral) y Achar (método diferencial), las que se explican a continuación.

Método de Coats-Redfern

Integrando la ecuación (1) y aproximando la integral de temperatura (la cual no tiene solución exacta) mediante la serie asintótica y tomando hasta el primer término de la serie, al aplicar logaritmos y reordenar, para un programa de calentamiento no isotérmico se tiene la ecuación (3):

Graficando el miembro izquierdo para cada función g(a) con respecto a 1 000/T se obtiene E y Z de la pendiente y el intercepto respectivamente. El modelo se obtiene por el mejor ajuste lineal a través del coeficiente de correlación.

Desde el punto de vista matemático, que un modelo cinético muestre un r ≈ 1, significa que los datos experimentales se ajustan mejor a la expresión matemática que representa dicho modelo en particular. Desde el punto de vista físico significa, que la velocidad de esa reacción en particular está determinada por ese modelo, porque es la etapa más lenta de la misma [8].

Ecuaciones diferenciales:

Estas son más empleadas cuando se puede medir directamente la velocidad del cambio de la propiedad física da/dt que, al tener solución exacta, brinda más confiabilidad en los resultados [9].

Método de Achar o Método diferencial directo

A partir de reordenar y aplicar logaritmo natural a la expresión (1) se obtiene la (4):

Al graficar el miembro izquierdo vs. 1 000/T para cada función f (a), el modelo cinético que mejor describe la reacción es seleccionado a partir de los valores del coeficiente de correlación (r); la Ea (kJ/mol) y el factor pre exponencial (Z) se calculan de la pendiente y del intercepto respectivamente. Entonces, el valor de la pendiente estará relacionado con el término E/R y el intercepto con ln Z/ß [9].

 

MATERIALES Y MÉTODOS

Las maderas estudiadas son de origen ecuatoriano y se obtuvieron en el Centro de Comercialización ubicado en Portoviejo, Manabí. Allí, el tronco es acerado y preparado para su comercialización en dependencia de sus diferentes usos. Las muestras objeto de estudio, forman parte de los residuos forestales del centro de comercialización y se escogieron en forma de pequeños trozos por un mes, en particular los días 1, 10, 20 y 30.

Estos trozos fueron transportados debidamente empacados hasta el laboratorio BIOLAB de la Universidad Carlos III de Madrid. En dicho laboratorio se trituró cada biomasa por separado, pero uniendo los días de recolección 1-20 y 10-30, utilizando molino de cuchillas Tipo MS 2000 marca ReTsch hasta tamaño de partícula de 4 mm (medido con el tamiz interior del molino). Posteriormente se mezclaron ambas porciones para la misma biomasa y se trituró dos veces más en dicho molino, hasta disminuir tamaño de partícula a 2 y menor a 1 mm respectivamente.

A continuación, se seca el material en estufa universal marca Memmert, según Norma UNE-EN_14774-1:2010. Finalmente se tamizó en una máquina cribadora AS 200 marca ReTesch durante 15 min, utilizando una frecuencia 180 vibraciones/min y se selecciona la porción cuyo tamaño de partícula se encuentra comprendido entre 53-106 micras para cada biomasa. Las cantidades de sólidos triturados de cada especie forestal fueron reducidas, aplicando varias veces la técnica de cuarteo, hasta obtener 4 kg de muestra homogénea, para cada una de las maderas estudiadas. Las mismas se almacenaron en recipientes de polietileno, lugares frescos no expuestos al sol y protegidas de contaminación.

El análisis inmediato de las muestras se realizó utilizando dos equipos: la humedad (Norma UNE-EN_14774-1: 2010) y materia volátil (Norma UNE-EN_15148: 2010) a través de un TGA Q 500 TA Instruments, mientras que cenizas (Norma UNE-EN_14775:2010) en una mufla marca Lenton, SAF. El poder calórico superior se realiza en un calorímetro Parr 6300 según norma ASTM D 1989-96. Utilizando muestras de 1+/-0.5 g por triplicado para garantizar su repetividad. Los resultados de análisis inmediato para ambas maderas se compararon por el Método de Observaciones Pareadas.

Para el análisis termogravimétrico se empleó equipo TGA Q500, marca TA Instruments. Se utilizaron cuatro velocidades de calentamiento 5, 15 25 y 35 ° C/min para ambas biomasas, con un flujo de nitrógeno de 60 ml/min para garantizar la atmósfera inerte en muestras de 9 +/- 0,5mg. El análisis estadístico de la influencia de la velocidad de calentamiento sobre la variable respuesta masa residual, se realizó utilizando el software Statgraphics Centurion y se aplicó una Comparación Múltiple de Muestras, utilizando el criterio de Cochran y el criterio LSD de Fisher. Se fijaron valores de temperatura desde 50 – 750 °C, con una variación de 50 °C para las velocidades de calentamiento ya definidas y ambas biomasas. Los gráficos de porciento de masa residual versus temperatura se realizaron con el software Origin 6.1.

El análisis térmico simultáneo se efectuó en un equipo NETZSCH STA 449 F3m, con técnicas TGA, ATD y DSC combinadas. Se utiliza la velocidad de calentamiento 15 ° C/min y un flujo de nitrógeno de 60 ml/min para garantizar la atmósfera inerte en muestras de 0,5 mg.

Para el estudio cinético aplicando el método de ajuste de las funciones, tanto para la Ecuación de Coats (integral), como la ecuación de Achar (diferencial), se utiliza el software Microsoft Excel 2010 para el cálculo de cada uno de los modelos cinéticos seleccionados y para el análisis de correlación lineal se utilizó el software Origin 6.1, a través del cual se calcula r (coeficientes de correlación lineal) y Ea (energía de activación).

 

RESULTADOS Y DISCUSIÓN

Análisis elemental e inmediato de las maderas estudiadas

La caracterización de la biomasa por análisis elemental involucra la determinación de los contenidos de carbono, nitrógeno, hidrógeno, azufre y oxígeno en las maderas Fernán Sánchez y teca. Mientras que el análisis inmediato permite estimar de manera sencilla el comportamiento de un combustible, al determinar: humedad, volátiles, carbono fijo (o char) y cenizas. Previo a la realización del análisis cualitativo de dichos resultados, se efectúa una Prueba de Observaciones Pareadas para comprobar si existen diferencias significativas entre los valores determinados para ambas maderas. Los valores experimentales y los resultados estadísticos de desviación estándar y P valor son presentados en la tabla 2.

TABLA 2. ANÁLISIS ELEMENTAL DE LAS MADERAS INVESTIGADAS
(VALORES EXPERIMENTALES Y RESULTADOS ESTADÍSTICOS)

	teca			Fernán Sánchez			DS	P valor
C(%)	49,54	49,56	49,55	46,22	46,26	46,25	1,15 · 10^-2	4,06.10^-6
N(%)	0,18	0,19	0,23	0,38	0,36	0,34	4,58 . 10^-2	2,63.10^-2
H(%)	4,03	4,06	4,00	4,12	4,13	4,17	5,29.10^-2	6,92.10^-2
S(%)	0,52	0,49	0,47	0,33	0,37	0,36	4,36.10^-2	3,08.10^-2
O(%)	44,35	44,37	44,36	48,92	48,91	48,93	1,73.10^-2	4,81.10^-6

Del análisis estadístico realizado se demuestra que, existen diferencias significativas en el contenido porcentual de C, N, S y O entre las dos maderas estudiadas, porque los p valor son menores que 0,05; no así para el contenido de Hidrógeno. Es conocido de la literatura que la composición de la madera puede variar de una especie a otra y dentro de una misma especie de acuerdo a su hábitat, edad y por la parte del árbol objeto de estudio (raíz, tallo, hojas, etc.), entre otros [1], de ahí que la mayor parte de los contenidos elementales varíen significativamente entre una madera y otra.

Una vez realizado este análisis estadístico se comparan los valores medios del contenido elemental de las maderas investigadas, con los resultados reportados en la literatura para materiales lignocelulósicos de características similares, que han sido tradicionalmente estudiados y utilizados con fines energéticos (ver tabla 3). El resultado del % C de la teca Ecuatoriana es similar al reportado para la teca Nigeriana por Balogun [9] y para el bagazo de la caña de azúcar [10]; no así el de Fernán Sánchez que es algo menor. El mayor contenido de carbono explica el también mayor poder calórico superior en las tecas. Ha sido reportado que, los recursos biomásicos, comparados con los combustibles fósiles sólidos como los carbones bituminosos (hulla), se caracterizan en términos generales por presentar un bajo contenido en carbono (menor que 50 %) y un alto contenido en oxígeno (mayor del 40 %) [1]. Los contenidos de carbono y oxígeno en las maderas estudiadas coinciden con estos valores.

Los porcientos de N y S menores que 1 % en ambas biomasas (tabla 3), garantizan menores emisiones de NOx y de SOx al ambiente, lo que reduce su impacto ambiental. Contenidos de humedad menores al 5 % caracterizan las biomasas lignocelulósicas y justifican aprovecharlas a través de su pirólisis.

TABLA 3. COMPARACIÓN DE LA COMPOSICIÓN ELEMENTAL DE LAS MADERAS
ESTUDIADAS CON RESULTADOS PROPUESTOS POR OTROS AUTORES

Componentes	teca	Fernán Sánchez	teca nigeriana [9]	Bagazo de caña [10]
C	49,55	46,24	49,6	49,6
N	0,20	0,36	0,4	0,21
H	4,03	4,14	6,3	5,71
S	0,49	0,35	-	0,03
O	44,36	48,91	43,7	41,1

TABLA 4. RESULTADOS DEL ANÁLISIS INMEDIATO DE LAS MADERAS Y SU
COMPARACIÓN CON LO REPORTADO POR OTROS AUTORES

Componentes	teca	Fernán Sánchez	teca nigeriana	Bagazo de caña	Paja de maíz
Humedad (%)	3,80	4,28	-	-	8,67
Volátiles (%)	76,77	75,49			70,87
Carbón Fijo (%)	17,68	14,47	3,8		14,87
Cenizas (%)	1,75	5,76	0,7	3,31	5,53
HHV (MJ/kg)	19,07	18,04	19,8	18,9

La biomasa lignocelulósica en comparación con el carbón bituminoso tiene un alto contenido de volátiles (entre 60 y 80 %) que pueden suponer más de dos terceras partes del poder como combustible. Los volátiles en teca y Fernán Sánchez son de 76,77 % y 75,49 % respectivamente y son resultados fundamentalmente de la degradación de la hemicelulosa y celulosa (tabla 4).

El mayor contenido de cenizas de Fernán Sánchez (tabla 4) es un factor que influye negativamente en su poder calórico. Este es un parámetro de gran importancia cuando se utiliza la biomasa como materia prima en procesos termoquímicos, debido a su influencia directa en la eficiencia energética y su tendencia a elevar los costos de mantenimientos, producto a las incrustaciones que se crean por la fusión de las cenizas.

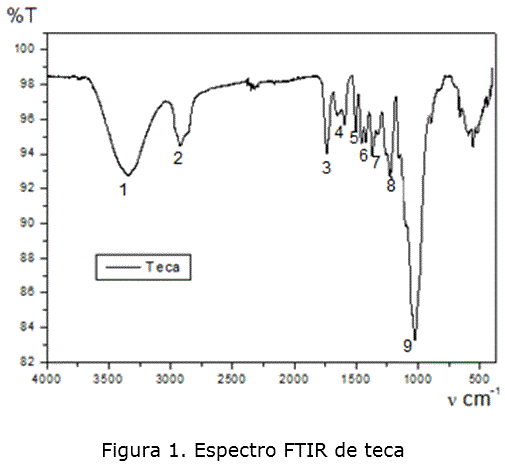
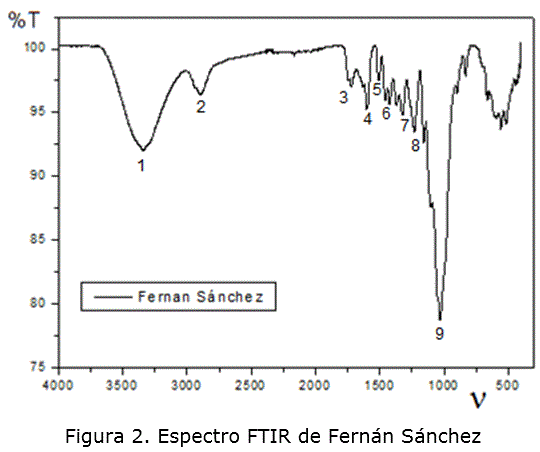
Caracterización de las biomasas por espectroscopia infrarroja

Los resultados obtenidos por FTIR para teca y Fernán son los mostrados en las figuras 1 y 2. La asignación de las bandas fundamentales que corresponden a las vibraciones características de los componentes principales de ambas biomasas, se encuentran en la tabla 4, con lo que se identifica la presencia de los mismos y coinciden con lo reportado por otros autores [11].

En dicha tabla se pueden identificar varias bandas asociadas a los grupos funcionales de los componentes mayoritarios de la biomasa y se observa en la zona de más alta energía, la banda intensa y ancha relacionada con agua no enlazada y los grupos OH, como fue identificado. Además, se distinguen pequeñas diferencias en cuanto a los valores de las frecuencias experimentales y reportadas, lo que se debe a pequeños corrimientos de las bandas, ocasionados por interacciones entre sustancias, lo que anuncia la complejidad del material objeto de estudio.

TABLA 5. ASIGNACIÓN DE LAS PRINCIPALES BANDAS PRESENTES EN
EL IR-TF DE AMBAS MADERAS

	Frecuencia Experimental (cm^-1)	Asignación	Frecuencia Reportada [11] (cm^-1)	Polímero asociado
1	3 345	O-H Stretching	3 421	-
2	2 928	C-H Stretching	2 937	Lignina
3	1 730	C=O Stretching Cetona y Aldehído	1 730	Hemicelulosa
4	1 596	Anillo aromático C=O Stretching	1 595	Lignina
5	1 502	Anillo Aromático	1 500	Lignina
6	1 419	Deformación en el plano C-H	1 425	Lignina
7	1 336	Vibración C-H Deformación en el plano O-H	1 335	Hemicelulosa, Celulosa y Lignina
8	1 220	C-C y C-O Stretching	1 215	Lignina
9	1 036	C-O, C=C,C-C-O Stretching	1 035	Hemicelulosa,Celulosa y Lignina

Análisis de la influencia de la velocidad de calentamiento (ß) sobre las curvas ATG para ambas maderas

Los perfiles térmicos por ATG para ambas muestras, a diferentes velocidades de calentamiento (5, 15, 25 y 35 °C/min), se muestran en la figura 3 y se utilizan para llevar a cabo análisis estadístico, con el fin de conocer si la velocidad de calentamiento influye sobre las curvas térmicas, representado en este caso a partir de la masa residual considerada variable respuesta.

Al comparar los perfiles térmicos por ATG de las biomasas objeto de estudio se observa una gran similitud para una misma biomasa a diferentes velocidades de calentamiento, lo que puede indicar que aparentemente la ß no influye en la forma de la curva térmica. Aunque es evidente que un aumento de ésta provoca un desplazamiento de las curvas hacia mayores temperaturas, lo que se explica porque se suministra más calor a la muestra en el mismo tiempo. Además, esa ß mayor afecta la primera etapa relacionada con la deshidratación del material.

En las tablas 6 y 7 se muestran las variables dependiente e independiente del análisis estadístico seleccionado, en este caso la prueba de Comparación Múltiple de Muestras utilizando el criterio de Cochran, para analizar la homogeneidad de la varianza; en la que se escoge la temperatura como variable control y se analizan la variación del porciento de masas residuales.

TABLA 6. DATA DE LA TECA, PARA EL ANÁLISIS DE LA INFLUENCIA DE LA ß SOBRE
LA MASA RESIDUAL

Temperatura (°C)	B = 5 °/min	B = 15 °/min	B = 25 °/min	B = 35 °/min
50	97,754	98,256	98,28	98,215
100	95,232	96,309	96,35	96,333
150	94,941	96,102	96,17	96,144
200	94,238	95,636	95,79	95,779
250	89,972	92,966	93,61	93,907
300	69,309	80,09	83,77	85,877
350	28,78	43,488	53,25	59,864
400	23,514	24,115	25,02	26,069
450	21,297	21,39	22,07	22,761
500	20,1	19,968	20,51	21,036
550	19,258	19,059	19,55	20,048
600	18,62	18,365	18,82	19,293
650	18,177	17,865	18,29	18,705
700	17,821	17,551	17,95	18,318
750	17,426	17,269	17,69	18,052

El valor de la probabilidad de esta prueba fue de p = 0,998 0 para Fernán Sánchez y p = 1,000 0 para teca, los cuales son mayores que el valor establecido para el nivel de significación (α = 0,05), por lo que no existen diferencias estadísticamente significativas entre las dispersiones de los grupos analizados, es decir los grupos son homogéneos.

Un criterio adicional fue obtenido al analizar las posibles diferencias entre los valores medios de los grupos, utilizando la prueba de Rangos Múltiples siguiendo el criterio LSD de Fisher (Lowest Significant Difference). El análisis realizado ratifica que no existen diferencias significativas entre los valores medios de los grupos analizados, de lo cual se infiere que la ß no influye en el porciento de masa residual a un 95 % de probabilidad. Estos resultados estadísticos nos permiten utilizar indistintamente cualquiera de las curvas térmicas para el análisis cinético, utilizando el método de ajuste de las funciones.

TABLA 7. DATAS DE FERNÁN SÁNCHEZ PARA EL ANÁLISIS INFLUENCIA DE LA ß
SOBRE LA MASA RESIDUAL

Masa Residual (%)
Temperatura (°C)	B = 5 °/min	B = 15 °/min	B = 25 °/min	B = 35 °/min
50	98,51	95,69	98,44	98,20
100	96,59	96,13	96,34	96,20
150	95,98	95,57	95,77	95,67
200	95,16	95,04	95,34	95,29
250	88,48	91,21	92,37	92,73
300	65,75	75,09	79,64	81,86
350	29,33	39,79	49,82	55,26
400	25,51	26,10	27,19	27,02
450	23,47	23,70	24,59	24,21
500	21,54	21,64	22,85	22,48
550	20,67	20,66	21,386	20,83
600	19,35	19,87	20,67	20,09
650	18,53	18,45	19,29	18,99
700	18,14	18,07	18,72	18,08
750	17,75	17,78	18,41	17,80

Curvas térmicas y análisis cinético del craqueo pirolítico de las biomasas investigadas

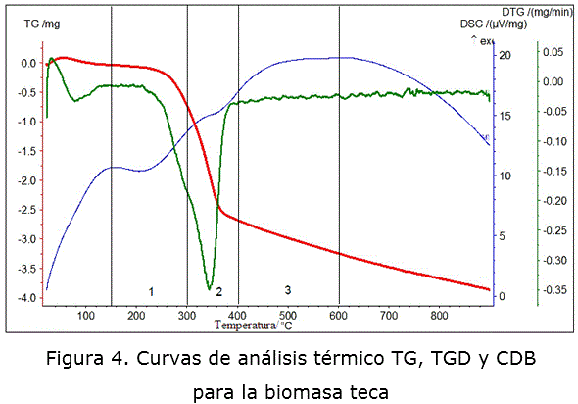
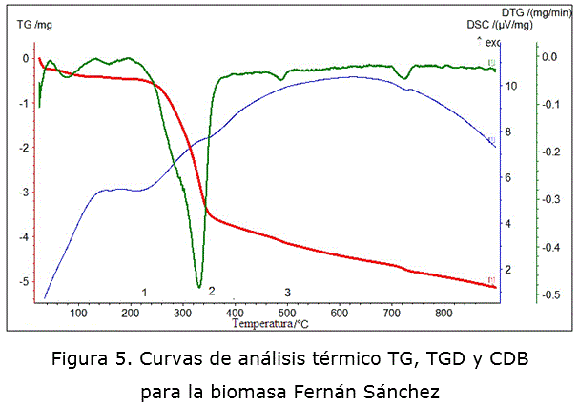
El análisis térmico es un conjunto de técnicas termoanalíticas en el que se mide una propiedad física de la sustancia, cuando la muestra se somete a un programa de temperatura. El perfil térmico de la biomasa lignocelulósica es aproximadamente la suma de las contribuciones de sus constituyentes fundamentales, hemicelulosa, celulosa y lignina y es característico de estos materiales [12]. Algunos estudios por ATG han revelado, que la degradación de estos componentes tiene lugar en rangos de temperaturas muy concretos, indicando que etapas claves en el proceso de descomposición de la biomasa ocurren en intervalos de temperatura específicos [5].

Con base en lo anterior y en los evidentes cambios que experimentan las curvas ATG y TGD, en los registros térmicos simultáneos de las biomasas objeto de estudio representados en las figuras 4 y 5, se identifican en las mismas 3 etapas involucradas en el craqueo pirolítico de estos materiales y que están relacionadas con la desvolatilización de la hemicelulosa, celulosa y lignina respectivamente. Otros autores [5, 8, 9, 13] han considerado la existencia de estas etapas, en las que prevalece la ocurrencia de las reacciones ya referidas. Estos intervalos de temperatura que identifican dichas etapas y reacciones, constituyen la base para la realización del estudio cinético.

La cinética del craqueo pirolítico de la biomasa describe el desarrollo de la reacción en función de la temperatura y es importante porque ofrece información relacionada con el diseño y dimensionamiento de los reactores para el escalado tecnológico.

A continuación, se discuten los resultados obtenidos al abordar la cinética de las 3 etapas involucradas en este proceso, cuando se aplican el método de ajuste de las funciones y en particular las ecuaciones de Coats (Integral) y Achar (Diferencial).

De forma general, para la selección del modelo cinético se utiliza el criterio del coeficiente de correlación lineal cercano a uno, debido a que las ecuaciones cinéticas utilizadas responden a una línea recta. Cuando para una reacción o etapa del proceso en particular, varios modelos presentan valores de r cercanos entre ellos y próximos a uno, se considera hasta un Δr = 0,06 para distinguir los modelos más probables, dentro de una misma ecuación cinética, en este caso Coats o Achar. Luego de identificado los modelos más probables, se comparan los resultados obtenidos para ambas ecuaciones cinéticas y se escogen los modelos cinéticos que se repiten entre los probables, como los que determinan la velocidad de la reacción, para esa etapa del proceso de descomposición pirolítica [8, 9, 14, 15].

Las tablas 8 y 9 muestran los resultados obtenidos al estudiar la cinética de la descomposición de la hemicelulosa contenida en las biomasas teca y Fernán Sánchez (etapa 1 en las figuras 4 y 5).

TABLA 8. DESCOMPOSICIÓN PIROLÍTICA DE LA HEMICELULOSA, PARÁMETROS CINÉTICOS
CALCULADOS AL UTILIZAR EL MÉTODO DE AJUSTE DE LAS FUNCIONES

TECA- HEMICELULOSA
	METODO DE COATS		METODO DE ACHAR
MODELO	r	Ea (KJ/mol)	r	Ea (KJ/mol)
D1	0,98	129,6	0,98	127,9
D2	0,98	133,0	0,97	134,5
D3	0,97	142,7	0,95	142,7
D4	0,98	137,3	0,87	45,2
F1	0,96	67,5	0,85	71,0
R1	0,98	60,6	0,90	56,3
R2	0,97	65,2	0,88	63,4
R3	0,96	67,2	0,87	65,9
A 0,5	0,98	127,0	0,94	150,7
A1	0,97	51,2	0,85	71,0
A2	0,54	0,7	0,67	37,1
A3	0,03	0,8	0,48	24,5
A4	0,10	5,5	0,34	18,2

A partir de los criterios ya referidos se seleccionan para ambas biomasas, los modelos D1, D2, D3 y A0,5 como los que determinan la velocidad de descomposición de la hemicelulosa, por ser los que se repiten entre los más probables para las ecuaciones cinéticas utilizadas.

Los valores de energías de activación para esta etapa se encuentran entre 127 - 150 kJ/mol para la teca y 125 - 154 kJ/mol para Fernán Sánchez. Resalta la gran coincidencia entre los parámetros cinéticos calculados para ambas biomasas y vuelven a estar los modelos difusivos entre los que determinan esta etapa, en relación al estudio cinético del craqueo pirolítico realizado a la madera Guachapelí (ecuatoriana) y el marabú (cubano) [14]. A diferencia de ese trabajo, para esta etapa se identifican un menor número de modelos cinéticos, particularmente a partir de la ecuación de Achar, lo que resulta explicable considerando la mayor exactitud de las ecuaciones diferenciales, utilizadas para estos estudios.

TABLA 9. DESCOMPOSICIÓN PIROLÍTICA DE LA HEMICELULOSA, PARÁMETROS CINÉTICOS
CALCULADOS AL UTILIZAR EL MÉTODO DE AJUSTE DE LAS FUNCIONES

FERNAN SANCHEZ- HEMICELULOSA
	MÉTODO DE COATS		MÉTODO DE ACHAR
MODELO	r	Ea (KJ/mol)	r	Ea (KJ/mol)
D1	0,96	128,6	0,94	133,6
D2	0,95	131,5	0,94	141,0
D3	0,93	142,2	0,93	149,5
D4	0,95	136,5	0,72	48,4
F1	0,93	66,9	0,78	74,8
R1	0,95	60,2	0,80	59,7
R2	0,94	64,9	0,79	67,1
R3	0,93	66,9	0,79	69,7
A 0,5	0,96	125,3	0,89	154,6
A1	0,94	50,2	0,78	74,8
A2	0,52	12,7	0,58	42,0
A3	0,03	0,1	0,42	29,5
A4	0,12	6,1	0,31	23,2

Las tablas 10 y 11 muestran los resultados cinéticos de la desvolatilización de la celulosa contenida en las biomasas teca y Fernán Sánchez, respectivamente (etapa 2 en las figuras 4 y 5).

En el caso de la teca los modelos que se seleccionan son D3, F1 y R3, a diferencia de Fernán Sánchez que son F1, A3 y A0,5. Si bien pudiera escogerse F1, es decir el crecimiento unimolecular como el modelo que determina la velocidad de reacción en esta etapa, porque es el único que se repite entre los más probables para ambos métodos y porque varios autores suponen a priori que estos procesos de descomposición pirolítica de biomasas lignocelulósicas están determinados por este modelo, no se excluyen los modelos de nucleación A3 y A0,5 porque son los que prevalecieron para esta etapa, durante los estudios cinéticos de la pirólisis de las maderas Guachapelí y Marabú [14]. Vale destacar, que es la única etapa en la que se seleccionan modelos cinéticos diferentes, para ambas biomasas.

Los valores de energía de activación están entre 115 - 255 kJ/mol para teca y 146 - 215 kJ/mol para Fernán Sánchez. Ambos coinciden con los calculados por otros autores para estos procesos [1, 8, 9, 12-16].

TABLA 10. DESCOMPOSICIÓN PIROLÍTICA DE LA CELULOSA, PARÁMETROS CINÉTICOS
CALCULADOS AL UTILIZAR EL MÉTODO DE AJUSTE DE LAS FUNCIONES

TECA- CELULOSA
	MÉTODO DE COATS		MÉTODO DE ACHAR
MODELO	r	Ea (KJ/mol)	r	Ea (KJ/mol)
D1	0,74	162,1	0,78	91,6
D2	0,81	203,5	0,94	161,6
D3	0,88	240,4	0,99	255,4
D4	0,82	205,5	0,68	132,9
F1	0,92	146,0	0,94	176,3
R1	0,71	75,8	1,00	5,2
R2	0,83	102,2	0,95	90,7
R3	0,87	115,0	0,94	119,3
A 0,5	0,48	121,5	1,00	342,6
A1	0,11	35,0	0,94	176,3
A2	0,78	113,2	0,76	108,0
A3	0,87	139,3	0,59	81,8
A4	0,90	152,3	0,47	68,8

TABLA 11. DESCOMPOSICIÓN PIROLÍTICA DE LA CELULOSA, PARÁMETROS CINÉTICOS
CALCULADOS AL UTILIZAR EL MÉTODO DE AJUSTE DE LAS FUNCIONES

FERNAN SANCHEZ- HEMICELULOSA
	MÉTODO DE COATS		MÉTODO DE ACHAR
MODELO	r	Ea (KJ/mol)	r	Ea (KJ/mol)
D1	0,68	149,6	0,15	43,6
D2	0,76	191,9	0,00	21,6
D3	0,84	228,8	0,72	118,4
D4	0,77	193,1	0,41	314,1
F1	0,89	141,5	0,72	68,3
R1	0,65	69,6	0,80	108,1
R2	0,78	96,2	0,11	20,5
R3	0,83	109,2	0,02	9,1
A 0,5	0,4	106,7	0,88	215,9
A1	0,22	45,1	0,72	68,3
A2	0,84	121,0	0,01	11,8
A3	0,91	46,3	0,40	37,1
A4	0,94	158,9	0,54	49,7

TABLA 12. DESCOMPOSICIÓN PIROLÍTICA DE LA LIGNINA, PARÁMETROS CINÉTICOS
CALCULADOS AL UTILIZAR EL MÉTODO DE AJUSTE DE LAS FUNCIONES

TECA- LIGNINA
	METODO DE COATS		METODO DE ACHAR
MODELO	r	Ea (KJ/mol)	r	Ea (KJ/mol)
D1	0,82	114,2	0,82	54,53
D2	0,87	131,0	0,94	84,28
D3	0,92	151,8	0,95	121,03
D4	0,89	136,3	0,74	71,59
F1	0,93	80,0	0,72	60,82
R1	0,79	50,7	0,67	9,18
R2	0,88	63,8	0,63	26,03
R3	0,90	69,5	0,68	37,62
A 0,5	0,72	101,1	0,94	155,97
A1	0,01	8,3	0,72	60,82
A2	0,46	38,1	0,12	16,76
A3	0,65	53,5	0,03	1,29
A4	0,71	61,3	0,01	6,44

TABLA 13. DESCOMPOSICIÓN PIROLÍTICA DE LA LIGNINA, PARÁMETROS CINÉTICOS
CALCULADOS AL UTILIZAR EL MÉTODO DE AJUSTE DE LAS FUNCIONES

FERNAN SANCHEZ -LIGNINA
	METODO DE COATS		METODO DE ACHAR
MODELO	r	Ea (KJ/mol)	r	Ea (KJ/mol)
D1	0,83	116	0,75	54,6
D2	0,87	133,1	0,91	83,1
D3	0,92	153,6	0,96	120,2
D4	0,89	138,1	0,68	72,1
F1	0,94	81,3	0,80	59,7
R1	0,79	51,6	0,47	10,4
R2	0,88	64,7	0,72	24,5
R3	0,9	70,4	0,77	36,2
A 0,5	0,73	102,9	0,96	155,4
A1	0,01	8,9	0,80	59,7
A2	0,49	38,1	0,12	14,3
A3	0,68	53,8	0,02	1,3
A4	0,75	61,6	0,03	9,2

Por último, la etapa de descomposición de la lignina contenida en las biomasas investigadas (Etapa 3 en las figuras 4 y 5), cuyos resultados cinéticos se presentan en las tablas 12 y 13, están determinadas por procesos difusivos y en particular los modelos D2 y D3, es decir difusión bidimensional y tridimensional con simetría esférica respectivamente, para ambas biomasas. Estos modelos coinciden con los determinados para esta etapa en las maderas Guachapelí y Marabú [14]. Los valores de energía de activación son de 84-151 kJ/mol para teca y de 83-153kJ/mol para Fernán Sánchez, los mismos concuerdan con los propuestos por otros autores.

 

CONCLUSIONES

Las características químicas y energéticas de ambos residuos madereros ecuatorianos demuestran sus potencialidades para ser utilizados en aplicaciones energéticas. No obstante, el de teca resulta ser más atractivo para estos fines. El análisis estructural por FTIR permitió identificar las vibraciones características de los constituyentes principales de ambas biomasas. La velocidad de calentamiento y el tipo de biomasa influyen en menor medida en la cinética de la descomposición pirolítica de los residuos estudiados, no así los intervalos de temperaturas que distinguen las principales etapas de este proceso y que están relacionadas con la descomposición de hemicelulosa, celulosa y lignina respectivamente. El estudio cinético realizado permitió demostrar que la primera y tercera etapa están determinadas por procesos difusivos (D1, D2 y D3) y en la segunda prevalecen modelos F1 y de nucleación (A3 y A0,5). El predominio de modelos diferentes a los F1 en estos procesos, demuestra el riesgo de asumir preliminarmente que es éste, sin calcularlo a partir de los datos experimentales. Los valores de energía de activación calculados para ambas biomasas, en sus diferentes etapas de desvolatilización, se encuentran entre 83 - 255 kJ/mol y coinciden con lo reportado por otros autores.

 

REFERENCIAS BIBLIOGRÁFICAS

1. SEBASTIÁN, N. F.; GARCÍA, G.; D Y REZEAU A. Energía Renovable. Energía de la Biomasa (I). Zaragoza: Prensa Universitaria de Zaragoza, 2010. ISBN 978-84-92774-91-3.

2. URIEN, P. A. Obtención de biocarbones y biocombustibles mediante pirólisis de biomasa residual. Tesis de Maestría, Oviedo, Universidad de Oviedo, Instituto de Investigaciones Energéticas, 2013.

3. ÁLVAREZ R. A. Caracterización química de biomasa y su relación con el poder calorífico. Tesis de Maestría, Oviedo, Universidad de Oviedo, Instituto de Investigaciones Energéticas, 2013.

4. VINUEZA, M. Ficha técnica de maderables. Ecuador Forestal, 2012.

5. NOGALES, S. Reducción de las emisiones asociadas a la combustión y pirólisis de la biomasa mediante diversos métodos. Tesis Doctoral. Universidad de Extremadura, 2015.

6. JANKOVIC, B. "Kinetic analysis of the no isothermal decomposition of potassium metabisulfite using the model-fitting and isoconversional (model-free) methods". Chemical Engineering Journal. 2007, 30, 12-22. ISSN 1385-8947

7. GALWEY, A.; BROWN, M. "Application of the Arrenius equation to solid state kinetics: can this be justified?". Termochimica Acta. 2002, 386, 91-98. ISSN 0040-6031

8. QUESADA, O.; TORRES, E.; ALFONSO, F. E. "Estudio de la degradación térmica del residuo de la naranja". Revista Cubana de Química. 2011, 23(1), 25-33. ISSN 0258-5995

9. BALOGUN, A. O.; LASODE, O. A.; MCDONALD, A. G. "Devolatilization kinetics and pyrolytic analyses of tectona grandis (teak)". Bioresourse Technology. 2014, 156, 57-62. ISSN 0960-8524

10. COBO, B. F. Pirólisis de residuos de cosecha de caña de azúcar (rac) como alternativa de aprovechamiento en procesos de cogeneración. Tesis de Maestría. Universidad del Valle, 2012.

11. XU, F.; YU, J.; TESSO, T.; DOWELL, F.; WANG, D. "Qualitative and quantitative analysis of lignocellulosic biomass using infrared techniques: A mini-review". Applied Energy. 2013, 104, 801–809. ISSN O306-2619

12. DAMARTZIS, TH.; VAMVUKA, D.; SFAKIOTAKIS, S.; ZABANIOTOU, A. "Thermal degradation studies and kinetic modeling of cardoon (Cynara cardunlucus) pyrolysis using thermogravimetric analysis (TGA)". Bioresource Technology. 2011, 102, 6230-6238. ISSN 0960-8524

13. NARANJO, R. Utilización energética de la biomasa ligno-celulósica obtenida del Dichrostachys cinerea mediante procesos de termodescomposición. Tesis de Doctorado. Universita Politecnica delle Marche, Italia, 2015.

14. RODRÍGUEZ, Mc .R.; QUESADA, O.; CANTOS, M. A.; BRITO, L. "Guachapelí contra Marabú y la cinética de sus pirolisis". Revista Cubana de Química. 2017, 29(3), 362 - 378 . ISSN 2224-5421

15. ROSS, A.; QUESADA, O.; CANTOS, M. A.; BRITO, L. Craqueo pirolítico de residuos madereros ecuatorianos. Trabajo de Diploma. Universidad de Oriente, Cuba, 2017.

16. PENEDO, M.; SÁNCHEZ, A.; FALCÓN, J. "Pirolisis de bagazo de caña a escala de laboratorio. Parte I: Influencia de condiciones de operación en el rendimiento de productos". Tecnología Química. 2008, 28, 61-70. ISSN 0041-8420.

 

 

Recibido: 21/12/2017
Aceptado: 3/03/2018

 

 

Dra. C. Omaida Quesada-González, Facultad de Ciencias Naturales y Exactas. Universidad de Oriente, Cuba, [e-mail]