ARTÍCULO ORIGINAL

 

Método para el modelado y prueba de Diagramas de Casos de Uso mediante redes de Petri

 

Method for modeling and test of Use Case Diagrams by Petri nets

 

 

Lionel Rodolfo Baquero Hernández^1*, Luis Enrique Argota Vega¹, Osviel Rodriguez Valdés¹, Febe Ángel Ciudad Ricardo²

¹Universidad de las Ciencias Informáticas, Facultad 6, Carretera a San Antonio de los Baños, km 21/2, Torrens, Boyeros, La Habana, Cuba. CP.: 19370
²Universidad de las Ciencias Informáticas, FICI, Carretera a San Antonio de los Baños, km 21/2, Torrens, Boyeros, La Habana, Cuba. CP.: 19370

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

El modelado de software es clave en el desarrollo de aplicaciones informáticas, es una forma gráfica de visualizar, construir y documentar un sistema, además de que pueden utilizarse para la comunicación con el cliente. Una red de Petri puede ser definida como una traducción gráfica o matemática de un sistema a eventos discretos con la cual se puede describir su comportamiento. En el presente trabajo se propone un método para el modelado y prueba de diagramas de caso de uso mediante redes de Petri. El método propuesto ha sido demostrado matemáticamente a través de una adaptación a la definición formal de las redes de Petri específica para estos tipos de diagramas.

Palabras clave: modelado de software, pruebas, redes de Petri, diagrama de caso de uso.

---

ABSTRACT

The modeling software is key to the development of informatical applications, is a graphic way of visualizing, constructing, and documenting a system, also it can be used for communication with the client. A Petri net can be defined as a graphical or mathematical translation of a discrete event system with which to describe their behavior. In this investigation is proposed a method for modeling and test use case diagrams using Petri nets. The proposed method has been mathematically demonstrated through an adaptation to the formal definition of Petri nets specific to these types of diagrams.

Key words: modeling software, testing, Petri nets, use case diagram

---

 

 

INTRODUCCIÓN

Las redes de Petri (PN, por sus siglas en inglés) son un formalismo que surge en 1962 con el trabajo doctoral de Carl Adam Petri ¨Kommunikation mit Automaten¨ (Comunicación con Autómatas), en Alemania (Petri, 1962). Una PN puede ser definida como una herramienta gráfica y matemática de modelación que se puede aplicar en muchos sistemas. Particularmente son ideales para describir y estudiar sistemas que procesan información y con características concurrentes, asíncronas, distribuidas, paralelas, no determinísticas y/o estocásticas (Meneses, 2002). Desde su aparición hace ya más de cinco décadas se han realizado numerosos trabajos que han desarrollado una estable teoría para la especificación y verificación de sistemas concurrentes. Sin embargo, la teoría clásica de redes se enfrenta al desafío de adecuarse a las nuevas necesidades de los sistemas informáticos que los ingenieros diseñan en la actualidad (Rosa, 2007).

En el proceso de análisis del software de la disciplina Ingeniería de Software se realiza la ingeniería o análisis de requisitos que es el uso sistemático de procedimientos, técnicas, lenguajes y herramientas para obtener el análisis, documentación, evolución continua de las necesidades del usuario y la especificación del comportamiento externo de un sistema que satisfaga las necesidades del usuario. Una vez recopilados los requisitos se crean un conjunto de escenarios que identifiquen una línea de utilización para el sistema que va a ser construido, estos escenarios son llamados casos de uso y facilitan la descripción de cómo el sistema se usará. En general, un caso de uso es, simplemente, un texto escrito que describe el papel de un actor que interactúa con el acontecer del sistema (Pressman, 2002).

El presente trabajo se ha desarrollado con el objetivo de proponer un método basado en la bibliografía consultada para el modelado y prueba de diagramas de caso de uso con PN, lo cual fue resuelto siguiendo las tendencias del modelado de software actual. El método propuesto ha sido matemáticamente demostrado mediante una adaptación a la definición formal de las redes de Petri específica para estos tipos de diagramas.

 

MATERIALES Y MÉTODOS

Definición formal de redes de Petri

Para la presente investigación se asumirá como definición formal de redes de Petri la de (Zapata, 2005), como se expone a continuación:

Una red de Petri es una cuádrupla donde P={p1,p2,...pn}, es un conjunto finito y no vacío de lugares, T={t1,t2,...tn}es un conjunto finito y no vacío de transiciones, , es la función de incidencia posterior.

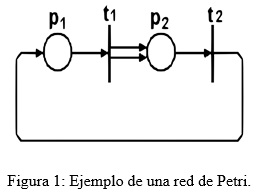
Una red de Petri se representa gráficamente por un grafo dirigido bipartido. Los lugares se representan por círculos, las transiciones por barras. Los lugares y las transiciones se conectan por arcos dirigidos. Un arco dirigido de un lugar pi a una transición tj existe sí y sólo sí . Análogamente, un arco dirigido de una transición tk a un lugar pi existe sí y sólo sí   . Cada arco se etiqueta con un entero natural, que se denomina peso del arco. En la Figura 1 se muestra un ejemplo de representación gráfica. En esta Figura se tiene una red de Petri con dos lugares y dos transiciones, el lugar pi está unido de la transición t1 mediante un arco , mientras que la transición t1 está unida al lugar p2 por dos arcos, entonces

Una red se representa matricialmente por medio de dos matrices. Sea (P) = n (número de lugares de la red), y sea (T) = m (número de transiciones de la red). Se denomina matriz de incidencia previa a la matriz:

en la que

Es decir, en las matrices de incidencia los lugares numeran las filas (i) y las transiciones numeran las columnas (j), y cada elemento (i,j) expresa la incidencia que el lugar i tiene sobre la transición j. La representación matricial para la red de la Figura 1 es de la siguiente manera:

Una red de Petri es pura si ninguna transición contiene un lugar que sea simultáneamente de entrada y de salida. La representación matricial de una red pura se simplifica definiendo una única matriz, C, denominada matriz de incidencia:

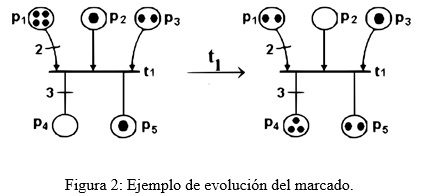
Las redes de Petri están dotadas de unos conceptos dinámico-estructurales como el marcado, la sensibilidad y la evolución del marcado. El marcado es la asignación de un número entero no negativo a cada lugar (número de marcas). Si (P) = n, entonces un marcado se representa, en forma matricial, por un vector de n elementos denominado vector de marcado M (Pi). La evolución del marcado le otorga a la PN un comportamiento dinámico que permite modelar evoluciones simultáneas de sistemas discretos. Una transición está sensibilizada si: , El disparo de una transición sensibilizada t, es representado por la expresión siguiente:

En la Figura 2 se puede ver la evolución del marcado de una red, una vez la transición t 1 sensibilizada ha sido disparada.

En las redes de Petri se tiene por lo general una secuencia de disparos a partir de un marcaje inicial M0, y se representa por una secuencia de disparo de transiciones tal que:

Se dirá que la secuencia es aplicable a partir de M0. A una secuencia de disparos σ se le asocia un vector característico σ, cuya i-ésima componente es el número de ocurrencias del disparo de ti en la secuencia σ. A partir de la definición de C y de la regla de evolución del marcado se puede obtener la ecuación de estado de una red de Petri (pura y marcada):

Una red de Petri temporizada, es un par (R,Z) tal que y Z es una función que asigna un número real no negativo, zi, a cada transición de la red. A este zi se le denomina tiempo de disparo de la transición ti. La evolución del marcado es idéntica a la de una red de Petri normal, la única diferencia es que el disparo de la transición ti tarda zi unidades de tiempo en suceder una vez quedó sensibilizado.

Modelado de diagramas de casos de uso mediante redes de Petri

El caso de uso es un concepto que ayuda a un analista a comprender la forma en que un sistema deberá comportarse. Le ayuda a obtener los requerimientos desde el punto de vista del usuario. Una de las finalidades del proceso de análisis es generar una colección de casos de uso (Schmuller, 2001), que posteriormente se traducirá en diagramas de casos de usos.  Los diagramas de caso de uso son una técnica para capturar requisitos o información de cómo un sistema o negocio trabaja, y están compuesto por los casos de uso, los actores que se pueden definir como algo con comportamiento, como una persona (identificada por un rol), sistema informatizado u organización (Larman, 2003), y las relaciones existentes entre ambos.

Para la construcción de diagramas de casos de uso utilizando redes de Petri, partiendo de su definición formal será necesario asumir que los actores y los casos de uso pertenecerán al conjunto P, las relaciones existentes entre ellos formarán parte de los conjuntos α y β en dependencia del lugar que ocupen en el grafo, y las transiciones o conjunto T constituirán subprocesos intermedios que deben existir entre unos y otros o el cambio de un estado a otro. Para ello se seguirán los patrones que se describen las Figura 3, Figura 4, Figura 5, Figura 6 para cada tipo de relación existente en estos tipos de diagramas respectivamente, que pueden ser de tipo comunicación, extensión, inclusión y de especialización o generalización (Megino, 2013).

Pruebas de redes de Petri basadas en diagramas de casos de uso

El flujo en estos tipos de diagramas comienza cuando un actor inicializa un caso de uso. Un diagrama de caso de uso es una PN pura y marcada por lo que para las pruebas de redes de Petri basados en un diagrama de caso de uso será necesario partir de lo siguiente:

• Para el conjunto P deberá cumplirse que la cantidad de lugares sea mayor que uno ((P)>1), dado que en un diagrama de caso de uso no puede existir solo un actor o solo un caso de uso. 

• El vector M0 tendrá m filas donde m=|p| (cantidad de lugares), los valores serán 1 en las filas que se correspondan con los lugares asociados a los actores que inicializan el sistema y 0 en otro caso.

• Los vectores M1, M2, ........Mk se calcularán a partir de la expresión 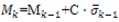, la cual es una adaptación a la definición formal de las PN específica para el modelado de diagramas de casos de uso, los valores serán 1 en las filas que se correspondan con los lugares marcados y 0 en otro caso. Donde k<=(P), dado que a partir de k=(P) el marcaje de la red es cíclico y se repetirá si son sensibilizadas las mismas transiciones.

• El vector característico 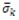tendrá n filas donde n=(T) (cantidad de transiciones), será actualizado para cada marcaje y los valores serán 1 en las filas donde se corresponda con las transiciones sensibilizadas y 0 en otros casos.

• Para el marcaje de la red deberá cumplirse que dos iteraciones consecutivas siempre serán distintas 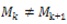, dado que si esto no se ocurre podrá ser interpretado como sinónimo de que el marcaje no ha cambiado de estado lo que significa que hay algún error en el diseño de la misma o esta no se corresponde con una PN basada en un DCU.

• En el marcaje de la red un lugar 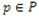no debe permanecer marcado por dos iteraciones consecutivas de la misma; si esto ocurre podemos interpretar que el actor o caso de uso correspondiente a este lugar no está correctamente relacionado con los demás.

• Durante el marcaje de la red todos los lugares 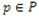deben haber sido marcados al menos en una ocasión si todas las transiciones han sido sensibilizadas.

Por lo que se puede plantear que si M0 coincide con Mk en alguna iteración para k<=(P) el DCU ha sido en teoría correctamente modelado evitando de esta forma los errores de concepto, aunque no necesariamente satisfaga las necesidades y especificaciones para el sistema en cuestión. Se puede demostrar esto aplicando el procedimiento descrito a los patrones de las Figura 3, Figura 4, Figura 5 y Figura 6.

Para el ejemplo de la Figura 3 se cumple que:

Entonces:

Por lo que queda demostrado matemáticamente que M0 = Mk lo que gráficamente significa que el actor es el que inicializa y finaliza el caso de uso, dado que el marcaje inicial y final se corresponderán con los lugares asociados a los actores. En las relaciones de tipo comunicación se cumple que M0 = Mk= M2, en las del tipo extensión M0 = Mk= M2 o M0 = Mk= M3 en dependencia de si se sensibiliza t2 o t3 respectivamente; para las del tipo inclusión M0 = Mk= M3 y en las del tipo generalización o especialización se deberá cumplir que M0 = Mk= M2 independientemente de si se sensibiliza t1 o t3. Esto es lo mismo que decir que un DCU modelado con PN está diseñado correctamente si el marcaje final coincide con el inicial sin importar que transiciones han sido sensibilizadas para llegar a él en una iteración tal que k<=(P).

 

RESULTADOS Y DISCUSIÓN

El marco teórico (Sampieri et al., 2006) o revisión de la literatura (Creswell, 2012), (Mertens, 2014) evidenció con claridad la necesidad de adaptar la teoría clásica de las PN a las nuevas necesidades del software. Partiendo de esto se desarrolló un método basado en una adaptación de la definición formal de las mismas. Con la aplicación de este método se podrá evitar errores que comúnmente se cometen en el modelado de los DCU. Para la demostración de la efectividad de la investigación desarrollada y de los resultados arrojados se realizará un experimento como método empírico. Se asumirá en este caso la definición ofrecida por (Chagoya, 2008), quien plantea que el experimento es la actividad que realiza el investigador donde:

• Aísla el objeto y las propiedades que estudia, de la influencia de otros factores no esenciales que puedan enmascarar la esencia del fenómeno.

• Reproduce el fenómeno objeto de estudio en condiciones controladas.

• Modifica las condiciones bajo las cuales tiene lugar el fenómeno de forma planificada.

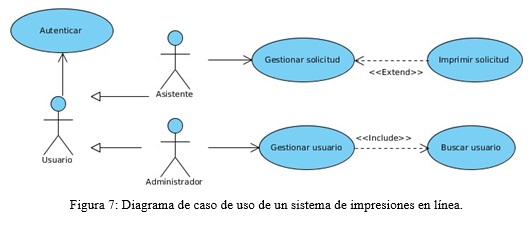
El método propuesto cobra verdadero sentido e importancia cuando el modelado de DCU se hace complejo para un sistema e incluye varios actores y tipos de relaciones. Para exponer los resultados de la investigación realizada se realizará una experimentación con un diagrama de caso de uso referente a un sistema de impresiones en línea que se muestra en la Figura 7.

Este diagrama al transformarlo en una red de Petri según el método propuesto queda modelado como se muestra en la Figura 8.

Si se aplica a esta red el método de prueba para redes de Petri basadas en diagramas de caso de uso propuesto se puede concluir que:

• (P) = 2 puesto que existen 3 actores y 5 casos de uso,
• (T)= 13 puesto que existen trece transiciones (t1, t2,..., t13),

 

• y para este marcaje existen tres posibles vectores característicos, en dependencia de si se sensibiliza t1, t3 o t4 respectivamente tendremos:

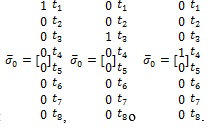
Por lo tanto se puede afirmar que M0 y Mk coincidirán en una iteración donde el valor de k dependerá de las transiciones que han sido sensibilizadas durante el marcaje de la red.

A continuación se enunciarán los posibles marcajes de la red y para cada uno el valor de k para el que M0 = Mk:

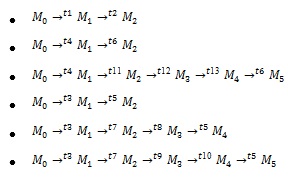
Para todos los posibles marcajes de la red se cumple que k<=(P), en ninguno de los casos dos iteraciones consecutivas coinciden, además de que ningún lugar se mantiene marcado por más de una iteración, quedando de esta forma comprobada la veracidad y efectividad del método propuesto.

 

CONCLUSIONES

El método propuesto podrá ser utilizado para cualquier diagrama de caso de uso que se desee representar matemáticamente. Se demostró durante la investigación la efectividad del mismo a partir de una adaptación del formalismo de las redes de Petri específica para los diagramas de casos de uso. Este método es capaz de detectar errores comunes que se cometen en el modelado de estos diagramas.

 

REFERENCIAS BIBLIOGRÁFICAS

Chagoya, E. R. Métodos y técnicas de investigación. Alianza, 2008.  

Creswell, J. Educational research: Planning, conducting, and evaluating quantitative and qualitative research. Pearson Education, 2012. 672p.

Larman, C. UML y Patrones. Madrid, Pearson Educación. 624p. 2003.

Megino, J. M. Tipos de relaciones en diagramas de caso de uso. [En línea] SEAS, 2013. [Consultado el: 19 de marzo de 2015]. Disponible en: [http://www.seas.es/blog/informatica/tipos-de-relaciones-en-diagramas-de-casos-de-uso-uml/].

Meneses, A. Redes de Petri. [En línea] CINESTAV, 2002. [Consultado el: 11 de marzo de 2015]. Disponible en: [http://computacion.cs.cinvestav.mx/~ameneses/pub/tesis/mtesis/node5.html].

Mertens, D. M. Research and evaluation in education and psychology: integrating diversity with quantitative, qualitative, and mixed methods. Sage Publications, 2014. 536p.

Petri, C. A. Kommunikation mit Automaten. Tesis Doctoral, Institut fur Instrumentelle Mathematik, Bonn. 1962.

Pressman, R. S. Ingeniería de Software, Un Enfoque Práctico. McGraw-Hill Companies. 640p. 2002.

Rosa, F. Redes de Petri móviles para la especificación y verificación de propiedades de seguridad en sistemas ubicuos. Tesis Doctoral, Universidad Complutense, Madrid, 2007.

Sampieri, R. et al. Metodología de la investigación. Mc Graw Hill, 2006. 850p.

Schmuller, J. Aprendiendo UML en 24 horas. Prentice Hall. 448 p. 2001.

Zapata, G. Sistema de diagnóstico de fallas para sistemas de transmisión de energía utilizando redes de Petri. Energética, 33: p. 5-14. 2005.

 

 

Recibido: 15/04/2016
Aceptado: 05/05/2016