ARTÍCULO ORIGINAL

 

Detección de Regiones de Interés en imágenes de la prueba de Papanicolaou

 

Detection of Regions of Interest in Images of the Papanicolaou Test

 

 

Reinier Rodríguez Guillén^1*, Yainet García García², Maykel Orozco Monteagudo³, Alberto Taboada Crispi³

¹ Centro de Ingeniería Cínica y  Electromedicina, Sagua la Grande, Cuba, [e-mail]
² Hospital Provincial Docente “Mártires del 9 de Abril”, Sagua la Grande, Cuba, [e-mail]
³ Universidad Central “Marta Abreu” de Las Villas, Santa Clara, Cuba, {morozco, ataboada}@uclv.edu.cu

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

La detección de anomalías en imágenes médicas es usada en la clasificación y detección de anormalidades. El objetivo de un detector de anomalías es la identificación de las diferencias en una serie de datos, sin tener ninguna información previa de sus propiedades. El objetivo de este trabajo es la construcción de un detector de anomalías para imágenes de la prueba de Papanicolaou, para lo que se diseñó e implementó un algoritmo que determinó regiones de interés. Este algoritmo se probó con 40 imágenes, 20 que sólo contenían células normales y 20 con células anómalas. El 100% de las imágenes con células anómalas presentó regiones de interés. De las 20 imágenes con sólo células normales, sólo 9 contuvieron regiones de interés. Por otro lado, el método propuesto incluyó en las regiones de interés al 92.43% de las células anómalas.

Palabras clave: Prueba de Papanicolaou, detección de anomalías, regiones de interés, clasificación, mapas de clasificación.

---

ABSTRACT

The detection of abnormalities in medical images is used in the classification and detection of abnormalities. The purpose of an anomaly detector is to identify the differences in a series of data, without having any previous information of its properties. The objective of this work is the construction of an anomaly detector for images of the Papanicolaou test, for which an algorithm that can determine regions of interest was designed and implemented. This algorithm was tested with 40 images, 20 containing only normal cells and 20 with abnormal cells. 100% of the images with anomalous cells presented regions of interest. Of the 20 images with only normal cells, only 9 contained regions of interest. On the other hand, the proposed method included 92.43% of the abnormal cells in the regions of interest.

Key words: Papanicolaou test, detection of anomalies, regions of interest, classification, classification maps.

---

 

 

INTRODUCCIÓN

El análisis de anomalías en imágenes médicas ha sido ampliamente abordado en la literatura científica (Herschman, 2003; Weissleder, 1999) .La Prueba de Papanicolaou también llamada citología de cérvix o citología vaginal, se realiza para diagnosticar el cáncer Cervicouterino, para conocer el estado funcional de las hormonas y para identificar las alteraciones inflamatorias a través del análisis de las células descamadas que se acumulan en un plazo de 28 días. Esta es una prueba que debe practicarse a todas las mujeres desde que inician su actividad sexual hasta los 65 años de edad. Anualmente se dan 490,000 casos de esta enfermedad en el mundo. Aproximadamente el 85% de las mujeres que fallecen por este tipo de cáncer viven en países en vías de desarrollo. La concentración más elevada está en el centro de América del Sur, con aproximadamente 71.000 casos por año (Contag, 2005). En el año 2010 un total de 11,818 mujeres en los Estados Unidos recibieron un diagnóstico de cáncer de cuello uterino y 3,939 murieron por esta enfermedad (UU, 2013).

La detección de anomalías (AD) es el proceso de detectar una pequeña fracción de datos que son diferentes de la mayoría o de un modelo definido por un conjunto de datos. Muchos estudios se basan en una definición negativa del problema: anomalías son porciones de datos que no se ajustan a la norma o al modelo de normalidad, los datos que se rigen por esta descripción son normales; aquellos que no se rigen al modelo son considerados anómalos. Las regiones anómalas son difíciles de detectar por lo que se utilizan una gran cantidad de rasgos (Taboada  A., Shali H., Orozco M., Hernández  D., & Falcón A., 2009).

Muchos estudios se han ocupado en la AD en imágenes médicas:

• Imágenes de tomografía computarizada de pulmón e imágenes de resonancia magnética (MR) de cerebro (Salgado  P. & Vendrell P., 2004) .

• Imágenes citométricas en patología donde se utiliza la patología quirúrgica para tomar contenido de ADN nuclear para analizarlo y dictar un pronóstico. Dentro de estos estudios están los del pulmón, esófago, ovario, endometrio, próstata, vejiga urinaria y papilar tiroideo (Cohen, 1996).

Dado que la prueba de Papanicolaou es revisada por especialistas humanos, el cansancio y la gran cantidad de muestras que estos tienen que diagnosticar ha dado lugar a equivocaciones tanto positivamente como negativamente, lo que ha abierto el camino al aparecimiento de técnicas del aprendizaje automatizado capaces de resolver estos problemas (Chiracharit, Yajie, Kumhom, Chamnongthai, & Babbs, 2007; Ikedo et al., 2007) . Por todo lo anterior el problema de nuestro trabajo será la ubicación de regiones de interés en la prueba de Papanicolaou para la detección de anomalías.

 

MATERIALES Y MÉTODOS

Para la realización de los experimentos se utilizaron 40 imágenes de la prueba de Papanicolaou.  Estas imágenes provienen de muestras del departamento de patología del Hospital Ginecobstétrico “Mariana Grajales”, en Santa Clara.  Las imágenes se tomaron usando una cámara digital 319CU. De estas 40 imágenes, 20 contenían células anómalas mientras que las 20 restantes sólo contenían células normales.  En total, estas imágenes de prueba contenían un total de 687 células anómalas.
En el presente trabajo se utilizaron tres tipos de rasgos para caracterizar a los parches de una imagen de la prueba de Papanicolaou. Estos fueron:

• Rasgos de color: 72 rasgos (Ocho estadísticos sobre 9 canales de los distintos espacios de color dan los 72 rasgos de color por parche) que se corresponden con 8 medidas estadísticas calculadas sobre los canales R, G y B del espacio de color RGB; los canales H, S y V del espacio de color HSV; y los canales L, a y b del espacio de color Lab.

• Rasgos de bordes: 5 rasgos que se describen en la sección.

• Rasgos de Textura: 78 rasgos de textura correspondientes a 13 rasgos basados en la matriz de co-ocurrencia calculada para los valores de escala 2, 4 y 8 y las orientaciones 0º y 90º.

En total se calcularon 155 rasgos por parche de la imagen. A continuación, se describe como se calculan estos rasgos.

Asumamos que un parche S viene dado en un espacio de color C.  Supongamos que un parche está compuesto por N píxeles {x1, x2,...,xn}. Para cada S se calculan medidas o un grupo de rasgos que se describen a continuación.

En muchos trabajos se han utilizado diferentes medidas de similitud entre histogramas (Crispi & Sahli, 2008; Webb, 2002), ya que éstas pueden determinar eficientemente diferencias a la hora de la clasificación. En este trabajo se utilizaron las distancias Matusita y Bhattacharyya (Taboada  A., et al., 2009) ya que con estas se obtuvo una mejor tasa de clasificación. Dados dos histogramas de  bins X = {x1, x2,...,xn} y Y = {y1, y2,...,yn}, estos tienen que cumplir que además de

La FIGURA 1 muestra el diagrama en bloque de la clasificación. A continuación, se explican en detalle los pasos del algoritmo anterior.

Paso 1. Cargar imagen.

Las pruebas se realizaron utilizando imágenes full-color de 0.78 Megapíxeles (1024x768) en formato TIFF (Tagged Image File Format).

Paso 2. Generar parches de la imagen.

Los parches se tomaron de tamaño 128x128 píxeles de forma tal que dentro de un parche cupiera una célula anómala.  La ventana deslizante utilizada para generar los parches se realizó con un solapamiento del 50% (FIGURA 2).  Para cada imagen se obtuvo 165 parches.

Paso 3.1 Calcular histograma en espacio de color Lab.

Para cada parche se calculan histogramas de 32 bins para los canales L, a y b.  Se realizaron experimentos para elegir entre los espacios de colores Lab y RGB para el cálculo de los histogramas.  Los mejores resultados se obtuvieron para el espacio de color Lab.

Paso 3.2 Clasificar (ROI o NoROI) el parche de acuerdo al histograma.

Cada parche se clasifica en ROI (Región de Interés) o NoROI (No Región de Interés) usando los histogramas en el espacio de color Lab y el método de los K Vecinos más Cercanos (K Nearest Neigbours, KNN).  Para la determinación de los valores de K y la distancia a usar se realizaron varios experimentos cuyos resultados se exponen más adelante. Los mejores resultados se obtuvieron para  y la distancia Bhattacharyya.  Para el cálculo de la distancia entre los histogramas de dos parches se promedia la distancia de acuerdo a cada canal, o sea:

donde P1 y P2 son dos parches y es el histograma del parche

Paso 3.3. Calcular rasgos del parche.

A partir de los 155 rasgos descritos en la sección anterior, se realizó una selección secuencial de rasgos, donde se escogieron los 12 rasgos significativos o relevantes.

Paso 3.4. Clasificar (ROI o NoROI) de acuerdo a los rasgos calculados.

Cada parche se clasifica en ROI (Región de Interés) o NoROI (No Región de Interés) usando los 12 rasgos y el método KNN.  Para la determinación de los valores de K y la distancia a usar se realizaron varios experimentos cuyos resultados se exponen más adelante.  Los mejores resultados se obtuvieron para K = 11 y la distancia Cityblock.

Paso 4. Construir Mapa de Importancia a partir de las clasificaciones de los parches de acuerdo a los rasgos y los histogramas.

El mapa de importancia M de la imagen I se calcula a partir de las clasificaciones de acuerdo a histograma y rasgos de cada uno de los parches en los cuales de dividió la imagen.

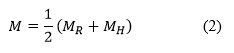
donde M_R y M_H son los mapas de importancia de acuerdo a la clasificación de los parches en rasgos e histogramas respectivamente.

La importancia de un pixel de acuerdo a la clasificación de basada en rasgos se define como:

donde es la cantidad de parches clasificados como ROI (de acuerdo a los rasgos) que contienen al pixel (i,j) y es la cantidad de parches clasificados como NoROI (de acuerdo a los rasgos) que contienen al pixel (i,j). Del mismo modo se define M_H.

5. Definir umbral T.  Declarar como Regiones de Interés aquellos pixeles con nivel de importancia superior a o igual T.

Definimos un umbral T. En nuestro trabajo, los mejores resultados se obtuvieron para T = 0.25. Los experimentos se realizaron para los valores de en el conjunto {0.25, 0.50, 0.75, 1.0}. Al final, la región de interés de la imagen I son los pixeles (i,j) que cumplen que

En muchos trabajos se han reportado la utilización de medidas para la evaluación de la calidad de la clasificación  (Joshi, 2002). Para la evaluación de la clasificación se usó la matriz de confusión, la cual deriva de una prueba que se la hace al clasificador en un conjunto de datos que no intervienen en el entrenamiento (Zhang, Fritts, & Goldman, 2008) . La siguiente (TABLA 1) muestra la matriz de confusión de un problema de dos clases.

Al valor N₀₀ se le denomina verdaderos positivos, N₀₁ falsos negativos, N₁₀ falsos positivos y N₁₁ verdaderos negativos.  A partir de estos valores se definen la Cantidad de Casos (N), la Tasa de Clasificación (TC) y la Tasa de Error ( ) en las ecuaciones (4) – (6), respectivamente.

 

RESULTADOS OBTENIDOS

Para la clasificación basada en histogramas se utilizó el método KNN.  Los espacios de colores que se probaron para la clasificación basada en histogramas fueron RGB y Lab. En la clasificación basada en histogramas se probaron las siguientes distancias entre histogramas.

• Distancia Bhattacharyya.

• Distancia Chi-Cuadrado.

• Distancia Intersección de histogramas.

• Distancia Kullback-Leibler

• Media armónica de la distancia Kullback-Leibler.

• Distancia Matusita.

Se probaron, además, distintos valores de K: 1, 11, 21 y 31.

Los mejores resultados se obtuvieron usando las distancias Bhattacharyya y Matusita. Los resultados para estas dos distancias y los distintos valores de K para el espacio de color Lab se muestran en la FIGURA 3.  Estas tasas de error se calcularon usando los histogramas de los 6600 parches con una validación cruzada con 10 grupos.

Con respecto a la clasificación basada en rasgos se calcularon 155 rasgos de color, textura y borde.

La clasificación se realizó utilizando el método KNN con las siguientes medidas de distancia:

• Distancia Chebychev

• Distancia Cityblock

• Distancia Coseno

• Distancia Euclidiana

• Distancia Euclidiana Estandarizada

Se probaron, además, distintos valores de K: 1, 11, 21 y 31.

Para cada distancia y valor de K se realizó una selección secuencial de rasgos usando el algoritmo KNN y una validación cruzada con 10 grupos.  Los mejores resultados se obtuvieron para la distancia Cityblock con K=11 como se muestra en la FIGURA 4.

Se calculó el mapa de importancia de una imagen, según la ecuación (2). A partir de este mapa de importancia se determinan las regiones de interés.  Se consideran píxeles de regiones de interés aquellos con importancia superior a un umbral T. Haciendo una comparación con todos los valores del umbral T analizados (T = 0.25, T = 0.5, T = 0.75, T = 1) se puede observar que la cantidad de pixeles en la ROI disminuye significativamente de 14.33% para T = 0,25 a 1.77% para T = 1, tomando el 100% como todos los pixeles de las imágenes usadas (FIGURA 5).

Por otro lado, las anomalías completamente (completamente dentro de la ROI) y parcialmente (más de la mitad de su área dentro de la ROI) incluidas en la ROI, disminuyen drásticamente a medida que aumentamos el valor del umbral T.   Por esta razón, elegimos un valor de compromiso para T (T = 0.25), de forma tal que incluyera la mayor cantidad de anomalías pero que también hiciera una reducción considerable de las regiones de interés.

Además, para T = 0.25, el algoritmo demostró su eficacia ya que encontró ROIs en todas las imágenes donde había células anómalas. En 11 de las 20 imágenes normales (donde no había células anómalas) no se encontraron ROIs.  En las 20 imágenes donde no había células anómalas, solo se seleccionó como ROI el 5.47% de su área (FIGURA 6).

Futuras investigaciones

La detección de regiones de interés en la prueba de Papanicolaou y en otras investigaciones sobre cáncer, Parkinson, y Alzheimer es de gran importancia ya que se sabe que estas están precedidas por cambios moleculares en células y tejido fino.

Los diferentes avances de AD en imágenes dependen del tipo de imagen que se trabaje: escala de grises, color, espectral, etc., o como se trabaje: completamente o parcialmente automatizado. Se distinguen también por si los detectores de anomalías son locales o globales. Esto depende del tamaño del área usada para construir el modelo de fondo. Acorde a la exploración se pueden identificar con algoritmos de correlación espectral y/o espacial (Hodge J. & Austin J., 2004).

Muchos estudios médicos se enfocan en órganos que pueden presentar diversos tipos de cáncer como el de pulmón, cerebro o mama. También existen algunos que se aplican a imágenes de células. Algunos se han dedicado al cuerpo entero donde se ha aplicado una segmentación Watershed para detectar tumores (Huang & Chen, 2004).Otras investigaciones se han ocupado en la detección de tumores en mamografía digital (Chiracharit, et al., 2007; Ikedo, et al., 2007). Los principales problemas de su detección son: la separación pobre de “distribuciones cruzadas” en las clasificaciones correctas dependiendo del valor de cada rasgo y el solapamiento de las distribuciones de rasgos normales y anormales (Chiracharit, et al., 2007; Ikedo, et al., 2007). En (Chiracharit, et al., 2007) se introduce la utilización de máquinas de soporte vectorial (SVM) basadas en el mapeo no cruzado y en la diferencia local de probabilidad (LDP). Otros problemas que se han introducidos son que la utilización de equipos convencionales y el cansancio de técnicos debido a la cantidad de imágenes puede provocar que se dejen de observar malformaciones. Se ha utilizado el detector de borde Canny para encontrar dichas anomalías (Ikedo, et al., 2007).

Un estudio que inspiró a este trabajo fue la detección de anomalías en imágenes de tomografía computarizada (Crispi & Sahli, 2008) donde se detectan las anomalías por la utilización métodos híbridos, como son la utilización de histogramas y rasgos. En esta investigación se confeccionó una interfaz gráfica de usuario (GUI) en la que se detectaban las anomalías existentes en las imágenes (FIGURA 7).

Como proyecciones futuras de esta investigación se encuentran:
1. La implementación de otros algoritmos para la clasificación basada en rasgos.
2. La implementación de otros algoritmos para la clasificación basada en histogramas.
3. La implementación de otro método para que la generación de mapas de importancia se pueda combinar con el método propuesto.

 

CONCLUSIONES

Se diseñó e implementó un algoritmo basado en histogramas y rasgos, usando el método de los K vecinos más cercanos, para la detección de regiones de interés para la detección de anomalías en imágenes de la prueba de Papanicolaou. Donde la distancia Bhattacharyya con K= 11 y la distancia Cityblock con K=11 dieron los mejores resultados respectivamente. Se construyeron mapas, a partir de las clasificaciones basadas en rasgos e histogramas, que representan las regiones de interés para la detección de anomalías en imágenes de la prueba de Papanicolaou. Se probó el método propuesto con imágenes reales:

• El 100% de las imágenes con anomalías mostró regiones de interés acorde al algoritmo propuesto. 

• El 55% de las imágenes sin anomalías no mostró regiones de interés según el método propuesto.

• El método propuesto redujo el área de interés en un 85.67% del total.

• El método propuesto excluyó de la región de interés a solo el 5.24% de las células anómalas.

 

REFERENCIAS BIBLIOGRÁFICAS

CHIRACHARIT, W., YAJIE, S., KUMHOM, P., CHAMNONGTHAI, K., & BABBS, C. F. (2007). Normal mammogram detection based on local probability difference transforms and support vector machines. IEICE TRANSACTIONS on Information and Systems, 90(1), 258-270.

COHEN, C. (1996). Image cytometric analysis in pathology. Human Pathology, 27(5), 482-493.

CONTAG, C. H. (2005). Using in vivo bioluminescence imaging to sheld light on cancer biology. IEEE, 93, 750-762.

CRISPI, A. T., & SAHLI, H. (2008). Experimental System for Image Anomaly Detection Based on Features and Distances.

HERSCHMAN, H. R. (2003). Molecular imaging:Looking at problems, seeing solutions. . Science.

HODGE J., & AUSTIN J. (2004). A survey of outlier detection methodologies. Artificial Intelligence Review, 22(2), 85-126.

HUANG, Y.-L., & CHEN, D.-R. (2004). Watershed segmentation for breast tumor in 2-D sonography. Ultrasound in medicine & biology, 30(5), 625-632.

IKEDO, Y., FUKUOKA, D., HARA, T., FUJITA, H., TAKADA, E., ENDO, T., et al. (2007). Development of a fully automatic scheme for detection of masses in whole breast ultrasound images. Medical physics, 34(11), 4378-4388.

JOSHI, M. V. (2002). On evaluating performance of classifiers for rare classes. Paper presented at the Data Mining, 2002. ICDM 2003. Proceedings. 2002 IEEE International Conference on.

SALGADO  P., & VENDRELL P. (2004). La imagen por resonancia magnética en el estudio de la esquizofrenia. Anales de psicología, vol. 20, p.261-272

TABOADA  A., SHALI H., OROZCO M., HERNÁNDEZ  D., & FALCÓN A. (2009). Anomaly Detection in Medical Image Analysis , (pp. 21): IGI Global.

UU, G. d. T. s. E. d. C. d. l. E. (2013). Estadísticas de cáncer en los Estados Unidos. Informe electrónico sobre incidencia y mortalidad 1999–2010.   Retrieved 9 de junio, 2014, from http://www.cdc.gov/uscs.

WEBB, A. R. (2002). Statistical pattern recognition (Second Edition ed.). UK: John Wiley & Sons,Malvern.

WEISSLEDER, R. (1999). Molecular imaging:Exploring the next frontier1. Radiology.

ZHANG, H., FRITTS, J. E., & GOLDMAN, S. A. (2008). Image segmentation evaluation: A survey of unsupervised methods. computer vision and image understanding, 110(2), 260-280.

 

 

Recibido: 01/09/2016
Aceptado: 20/12/2016