CIENCIAS NUCLEARES

 

Evaluación por Monte Carlo de los métodos de corrección de dispersión con empleando colimador pinhole

Monte Carlo evaluation of scattering correction methods in studies using pinhole collimator

 

Adlin  López Díaz¹, Sunay Rodríguez Pérez², Angelina Díaz García², Aley Palau San Pedro¹, Juan Miguel Martín Escuela¹

¹ Departamento de Medicina Nuclear, Hospital “Hermanos Ameijeiras” (HHA)
² Departamento de Física, Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN )

[e-mail]

---

RESUMEN

La dispersión es un efecto significativo a corregir para la cuantificación de actividad.  El objetivo del trabajo fue estimar la influencia de la dispersión en estudios de tiroides con y colimador pinhole (5 mm) empleando el método de Monte Carlo (MC) y evaluar la eficacia de los métodos de corrección de múltiples ventanas en este tipo de estudios. Para simular la geometría de la cámara gamma y el estudio de tiroides se utilizó el código de Monte Carlo GAMOS. Para validar la geometría del cabezal se simuló y verificó experimentalmente un maniquí de tiroides, comparando la sensibilidad estimada con la medida, experimentalmente en agua y aire. Para evaluar la influencia de la dispersión a escala clínica se simularon diferentes tamaños de tiroides y profundidades del tejido, se estimaron y compararon los resultados de los métodos de Triple Ventana, Doble Ventana y Doble Ventana Reducida. Se calcularon las diferencias relativas al valor de referencia obtenido por MC.  La geometría modelada fue verificada y validada. La contribución de la dispersión a la imagen fue significativa  y se ubicóentre el 27 y 40 % a escala no clínica. Las discrepancias de los resultados de los diferentes métodos de corrección de dispersión a escala clínica fueron significativas (p>95 %) y estuvieron en el rango entre 9 y 86 %. El método de mejores resultados fue el de la Doble Ventana Reducida (15 %) que mostró discrepancias entre 9 y 16 %. Se concluyó que el método de la Doble Ventana Reducida (15 %) fue el más eficiente de los estudiados.

Palabras claves: método de Monte Carlo, dispersión, corrección, yodo 131, colimadores, simulación computarizada, geometría.

---

ABSTRACT

Scattering is quite important for image activity quantification. In order to study the scattering factors and the efficacy of 3 multiple window energy scatter correction methods during thyroid studies with a pinhole collimator (5 mm hole) a Monte Carlo simulation (MC) was developed. The GAMOS MC code was used to model the gamma camera and the thyroid source geometry. First, to validate the MC gamma camera pinhole-source model, sensibility in air and water of the simulated and measured thyroid phantom geometries were compared. Next, simulations to investigate scattering and the result of triple energy (TEW), Double energy (DW) and Reduced double (RDW) energy windows correction methods were performed for different thyroid sizes and depth thicknesses. The relative discrepancies to MC real event were evaluated.  Results: The accuracy of the GAMOS MC model was verified and validated. The image’s scattering contribution was significant, between 27-40 %. The discrepancies between 3 multiple window energy correction method results were significant (between 9-86 %).  The Reduce Double Window methods (15%) provide discrepancies of 9-16 %. Conclusions: For the simulated thyroid geometry with pinhole, the RDW (15 %) was the most effective. 

Key words: Monte Carlo method, scattering, correction, Iodine 131, collimators, computerized simulation, geometry.

---

 

 

Introducción

Los estudios con colimador pinhole proporcionan imágenes de alta resolución de órganos de pequeñas dimensiones como la glándula tiroides y es una de las técnicas más usadas para estudiar el hipertiroidismo y su tratamiento con   [1,2]. Las posibles fuentes de error en la cuantificación de imágenes obtenidas con este tipo de colimador son: (a) los fotones dispersos que penetran a través de la apertura del colimador (penetración), (b) fotones dispersados por el objeto de estudio, (c) fotones dispersados por el material del colimador y (d) la atenuación de los fotones dentro del objeto de estudio [3,4]. Sin embargo, a pesar de los años de uso clínico de este aditamento, el impacto de las fuentes de error en la cuantificación de la actividad de no ha sido caracterizado en las diferentes condiciones clínicas de la tiroides. Tampoco ha sido evaluada la eficacia de los métodos de corrección disponibles, situación esta que con la necesidad de realizar tratamientos-paciente específico con costo efectivo,  gana vital importancia.

Una de las herramientas más utilizadas en medicina nuclear para asistir en el diseño y optimización de nuevos dispositivos de imagen médica nuclear es la simulación por Monte Carlo, que se emplea  de forma extensiva  en el perfeccionamiento, ajuste y evaluación de las principales características y parámetros de los sistemas de imagen médica nuclear [3, 5,6].

Este trabajo pretende evaluar, usando la simulación matemática, la influencia de la dispersión en la gammagrafía de la tiroides con mediante el empleo de un colimador pinhole (5 mm hole). Así como evaluar la eficacia de los métodos de corrección de múltiples ventanas en este tipo de estudios para mejorar la exactitud de la cuantificación de actividad y optimizar el tratamiento dosimétrico.

 

Materiales y métodos

Actualmente se cuenta con un grupo de programas generales cuyo código responde a la metodología Monte Carlo como EGS (Electron Gamma Sower), MCNP (Monte Carlo N-Particle Transport Code System) y GEANT-4 (GEometry ANd Tracking). Estos códigos, si bien incluyen modelos físicos validados, herramientas de modelación geométrica y eficientes utilidades de visualización, necesitan de una  curva empinada de aprendizaje por parte del usuario, lo que dificulta su uso a los no-especialistas. Debido a esto se han desarrollado programas construidos sobre los códigos anteriores que permiten una implementación sencilla y dinámica de los diferentes  sistemas PET, SPECT, Linac, etc. y sus características fundamentales, entre los que se encuentran: Sim-SPECT, basado en MCNP; PET-EGS, basado en EGS4; PeneloPET, basado en PENELOPE, GAMOS y GATE,   construidos sobre GEANT-4 [7].

El código Monte Carlo usado fue GAMOS (Geant4-Architecture for Medicine Oriented Simulation) basado en GEANT-4, pues constituye una plataforma optimizada para aplicaciones médicas  que permite su uso sin necesidad de tener amplios conocimientos del lenguaje de programación C++. Los parámetros de entrada están abiertos a cualquier isótopo o material que puede ser encontrado en el código de GEANT-4. Esta aplicación simula el paso de partículas a través de la materia e incluye su trayectoria, los modelos físicos y las colisiones para una geometría precisa. Posee también la capacidad de simular detectores de radiación y predefinir  parámetros típicos de la electrónica asociada, acotando los eventos de interés.  Esto favorece la modelación completa de geometría pues considera todas las interacciones del colimador y su impacto en el cristal, lo cual es esencial cuando son simulados emisores de fotones de altas energías (>300 keV) [8-10].

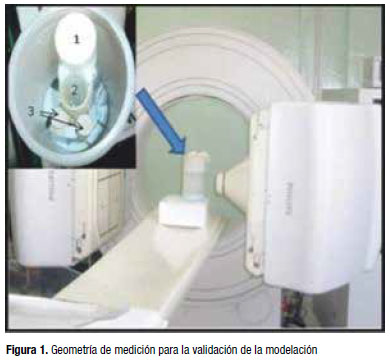
La exactitud del código fue validada calculando la sensibilidad del sistema y las diferencias absolutas entre la simulación y la medición física de este parámetro. Se simuló la geometría exacta del montaje experimental: la Cámara Gamma Philips Forte con colimador pinhole y el maniquí de tiroides que simula las mismas condiciones clínicas (1-columna, 2-tráquea y 3-tiroides, relleno con aire y con agua, ver Figura 1). El radioisótopo utilizado fue y la ventana energética, del 20 %.

Los resultados del estudio experimental fueron analizados con el software de procesamiento y análisis JetStream, empleado para los estudios clínicos de la Cámara Gamma Philips Forte. En el caso de la simulación se utilizó el programa AMIDE (Amide's a Medical Imaging Data Examiner) para calcular el número de eventos en cada ROI (Región de Interés).

Con el objetivo de realizar un estudio de la dispersión en condiciones clínicas reales, se construyó un modelo real y flexible de un maniquí antropomórfico voxelizado de tiroides, teniendo en cuenta la forma, volumen y masa real del órgano fuente. Se representó una diversidad de masas tiroideas con 16, 20, 24 y 28 g, respectivamente y se varió la profundidad del tejido entre la tiroides y el contorno del paciente en 6, 8, 10 y 12 mm.

El método de corrección más ampliamente usado consiste en la sustracción de la contribución estimada de la dispersión a la imagen, a partir de ventanas energéticas ubicadas en el espectro, en diferentes modalidades.

Se destacan en la literatura los métodos de la Triple Ventana, la Doble Ventana y la Doble Ventana Reducida [5,11-13].  Por esta razón, sobre la base de separar la dispersión de la radiación directa que incide en la ventana de cuentas del fotopico 364 keV (15 % y 20 %, valor de referencia), se estimaron y compararon los tres métodos de corrección de dispersión más utilizados: Triple Ventana (TV, con 2,5 % a cada lado), Doble Ventana (DV, con k=0,5) y Doble Ventana Reducida Inferior (DV Inferior, con 2,5 %). Se calcularon las diferencias relativas al valor de referencia “real” estimado por MC.

 

 

Resultados y discusión

Mediciones experimentales y validación de la geometría modelada

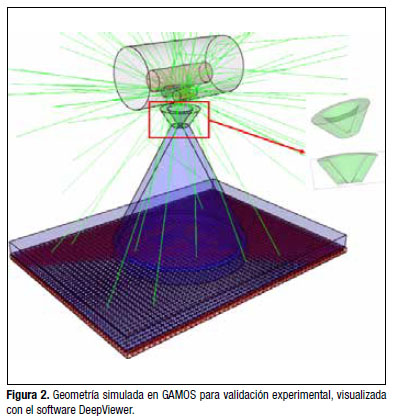
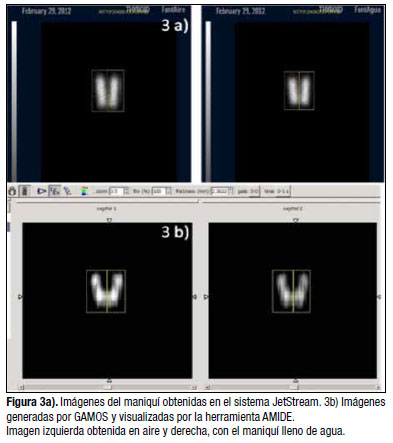
Se realizaron mediciones a una distancia de 6 cm entre el maniquí y el colimador, la condición de parada de la cámara fue 200 000 cuentas. Se realizaron mediciones con el maniquí relleno de aire y relleno de agua.  Para la validación de la simulación utilizando el programa GAMOS y obtener las 200 000 cuentas fue necesario simular 300 millones de partículas con una ventana del 20 % centrada en el pico de 364 keV. Los conteos dentro de las regiones de interés se calcularon con el programa AMIDE. En la Figura 2 se puede observar la geometría simulada en GAMOS y visualizada con el software DeepViewer. La Figura 3 muestra los resultados de las imágenes del maniquí obtenidas en la cámara gamma (3a) y las imágenes generadas por la simulación MC (3b). La sensibilidad medida
fue de 2,41 cps/μCi  y 1,82 cps/μCi en aire y agua, respectivamente, mientras que la simulada fue de 2,46 cps/μCi y 1,79 cps/μCien cada caso. Se calculó la sensibilidad (cps/μCi) como parámetro de referencia y evitar la influencia de otros parámetros que no fueron tenidos en cuenta en la simulación como la electrónica del sistema, las diferencias de uniformidad de los diferentes fototubos, etc. Las mayores discrepancias obtenidas fueron menores del 2 %. Esto demuestra la capacidad del programa GAMOS para reproducir datos experimentales y validar la plataforma de simulación desarrollada.

Para evaluar la influencia de la dispersión que producía el tejido blando se simularon, en esta geometría no clínica, espesores entre 5 y 15 mm (con densidad 0,967 ). La contribución de la dispersión a la imagen fue significativa y se ubicó entre el 27 y el 40 % a escala no clínica, similar a valores reportados por otros autores [5, 6, 11].

Evaluación de la dispersión a escala clínica

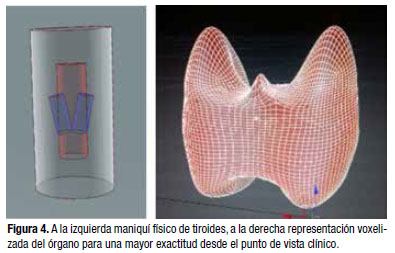
En la Figura 4 se puede observar la diferencia entre el modelo del maniquí físico usado para las mediciones experimentales y el maniquí antropomórfico voxelizado para la representación real del órgano de interés, que empleó masas totales de 16, 20, 24 y 28 g respectivamente y se varió la profundidad del tejido entre la tiroides y el contorno del paciente  en  6, 8, 10 y 12 mm.

Al analizar el número de cuentas generadas en las regiones de interés, se observó que a medida que aumentó la profundidad de la tiroidesen el cuello, el número de conteos disminuyó debido a la atenuación en el tejido. Además, se observó una pérdida de cuentas a medida que la masa del órgano aumentaba, lo que está ocasionado por la autoatenuación de las radiaciones en el interior del órgano.

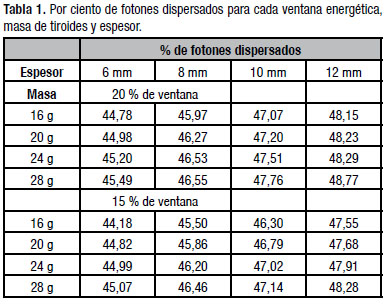
Se observó que el porciento de fotones dispersados en cada ventana energética aumentó con el espesor de tejido y con la masa de la tiroides. También se apreció que este aumento es significativo respecto a los valores encontrados en la geometría no clínica simulada anteriormente (ver Tabla 1). Estos valores mayores del 40 % corroboran la necesidad de la corrección eficaz del fenómeno físico para incrementar la exactitud de la cuantificación de actividad y demuestran la importancia reportada por otros autores de acercar las calibraciones dosimétricas a las condiciones clínicas para mejorar la exactitud [5,12-14].

Evaluación de varios métodos de corrección de dispersión a escala clínica

Se estudiaron dos configuraciones de tamaño de ventana central de 15 y 20 % para los tres métodos de corrección usados comúnmente en la clínica, con el objetivo de evaluar su desempeño para el sistema que se investigó y seleccionar la variante más exacta.

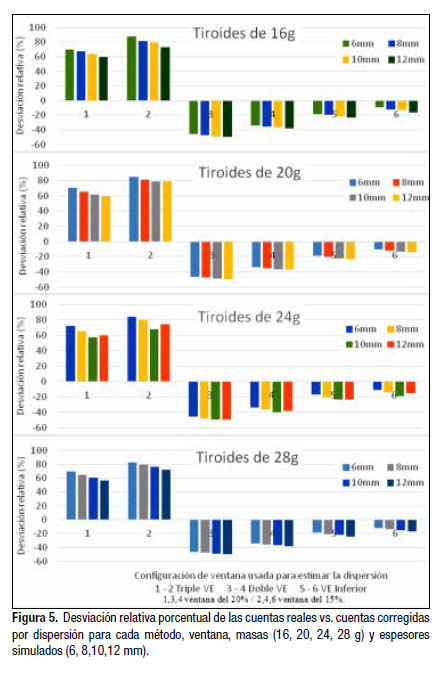
Las diferencias entre las estimaciones de cuentas por los diferentes métodos de corrección de dispersión a escala clínica fueron significativas (p>95 %). Las discrepancias de las cuentas corregidas vs. referencia (estimadas por MC) estuvieron en el rango del 9 al  86 %. La Figura 5 muestra el resultado de la desviación relativa porcentual encontrada para los tres métodos: Triple Ventana (TV, con 2,5 % a cada lado); Doble Ventana (DV,  con k=0,5) y Doble Ventana Reducida Inferior (DV Inferior con 2,5 %) para las diferentes tiroides (16, 20, 24, 28 g) y espesores simulados (6, 8,10, 12 mm).

Con el método de la Triple Ventana, las diferencias encontradas oscilan entre el 55 y  el 72 % para la ventana de 15 % y entre 67 y el 87 % para la de 20 %. En los casos en los que se usó el método de la Doble Ventana, las diferencias fueron del 45 al 49 % para 15 % y del 33 al 39 % para la ventana más ancha. Para el método de la ventana inferior las desviaciones se encuentran en un rango del 16 al 23 % para la configuración mayor y entre 9 y 16 % para la ventana más angosta. Se puede observar que para el método de la Triple Ventana se sobreestiman y para el método de la Doble Ventana se subestiman significativamente los fotones dispersados. Las configuraciones en las que se usó el método de la Ventana Inferior son, las de mejor concordancia con los datos aportados por el programa.

El método de la Triple Ventana Energética es uno de los más usados en la práctica clínica para la corrección de la dispersión del isótopo [12-13]. Este método  es un emisor de fotones de altas energías con rayos gammas de 364 keV (82 %), 637 keV (7,2 %) y 723 keV (1,8 %). Aunque estos dos últimos presentan baja intensidad, contribuyen significativamente en la imagen, ya que comparados con los fotones de 364 keV tienen relativamente baja atenuación en el paciente y una mayor probabilidad de penetrar los colimadores optimizados para los fotones de 364 keV en los colimadores paralelos. Los resultados obtenidos, empleando el método de la Triple Ventana con el colimador de pinhole, son contrarios a la experiencia con los colimadores de agujeros paralelos. Este estudio demuestra que este método presenta muy poca exactitud para el colimador de pinhole, pues sobrestimó hasta un 87 % los fotones dispersados. Estos resultados son apoyados por la investigación de  H. Deloar y colaboradores [3] que plantea que el colimador de tipo pinhole  disminuye en gran medida la penetración septal y provoca  que los fotones dispersados de mayor energía no aporten a la ventana el número de fotones que el método prevé y produzca  una sobreestimación del número de fotones dispersados, aun en la geometría no clínica de estudio. Este resultado implica que  este método, altamente indicado para estudios de cuantificación con colimador de agujeros paralelos, mediante el empleo de , producirá errores significativos si se utiliza el pinhole y estos errores se hacen mayores en el escenario clínico.
Los resultados obtenidos apuntan a señalar el método de la Ventana Inferior Reducida como el que estima, en mejor medida, el número de fotones dispersados, aunque los valores discreparon hasta un 16 % para la ventana del 15 % y hasta 23 % para la ventana del 20 %. Este método es el que deberá utilizarse en la práctica clínica para mejorar la exactitud de la cuantificación de actividad en estos estudios y para obtener imágenes 2D para la dosimetría-paciente específica.

 

 

Conclusiones

La contribución de la dispersión fue significativa en escenarios clínicos y no clínicos en geometría de la tiroides con pinhole. El  método de corrección de dispersión más eficaz fue  la Doble Ventana Reducida con el empleo de una ventana principal de 15 %.

Se recomienda realizar un estudio con maniquíes voxelizados en otros  escenarios clínicos que  planteen distribuciones no homogéneas de actividad para confirmar estos resultados.

Agradecimientos

Los resultados del programa son el  fruto de la acción de cientos de trabajadores vinculados a la salud y a la ciencia en Cuba. A todos ellos y en particular, al colectivo de trabajadores del Hospital Pediátrico de Tarará y a los trabajadores del CPHR vinculados al programa,  nuestro agradecimiento. 

 

 

Referencias bibliográficas

[1] STOKKEL  MP, HANDKIEWIC D, LASSMANN M, et. al. EANM procedure guidelines for therapy of benign thyroid disease. Eur J Nucl Med Mol Imaging. 2010; 37(11): 2218-2228.
[2] MERRILL S, HOROWITZ J, TRAINO AC, et. al. Accuracy and optimal timing of activity measurements in estimating the absorbed dose of radioiodine in the treatment of Graves’ disease. Phys Med Biol.  2011; 56(3): 557-71.
[3] DELOAR HM, WATABE H, AOI T & IIDA H. Evaluation of penetration and scattering components in conventional pinhole SPECT: phantom studies using Monte Carlo simulation. Phys. Med. Biol. 2003; 48(8): 995-1008.
[4] SMITH MF & JASZCZAK  J.  The effect of gamma ray penetration on angle-dependent sensitivity for pinhole collimation in nuclear medicine. Med. Phys. 1997; 24(11): 1701-9.
[5] ZAIDI H. Quantitative analysis in nuclear medicine imaging. Springer, 2006.
[6] LJUNGBERG M AND  STRAND S. Scatter and attenuation corrections in SPECT using density maps and Monte Carlo simulated scatter functions. J Nucl Med. 1990; 31(9): 1560-1567.
[7] ESPAÑA S, HERRAIZ JL, VICENTE E, et. al. PeneloPET, a Monte Carlo PET simulation tool based on PENELOPE: features and validation. Phys Med Biol. 2009; 54(6): 1723-1742.
[8] ALLISON J.  Geant4 developments and applications. IEEE Transactions on Nuclear Science.  2006; 53(1): 270 -278.
[9]  AMIDE: Amide's a Medical Imaging Data Examiner. AMIDE.exe 0.9.2 [software online]. Disponible en: http://amide.sourceforge.net  [May 2013].
[10] GAMOS 2011.  User’s Guide [guide online].   Disponible en:  http://fismed.ciemat.es/GAMOS/gamos_userguide.php.  [January 2013].
[11] NORRGREN K, SVEGBORN S, AREBERG J &  MATTSSON S. Accuracy of the quantification of organ activity from planar gamma camera images. Cancer Biother Radiopharm.  2003; 1(18): 125-131.
[12] DEWARAJA YK, LJUNGBERG M, GREEN AJ, et. al. MIRD Pamphlet No. 24: guidelines for quantitative 131I SPECT in dosimetry applications. J Nucl Med. 2013; 54(12): 2182-2188.
[13] DEWARAJA YK, FREY EC, SGOUROS G, et. al. MIRD Pamphlet No. 23: quantitative SPECT for patient-specific 3-dimensional dosimetry in internal radionuclide therapy. J Nucl Med. 2012; 53(8): 1310-1325.
[14] STABIN M. Uncertainties in internal dose calculations for radiopharmaceuticals. J Nucl Med. 2008; 49(5): 853-860.

Recibido: 23 de noviembre de 2016
Aceptado: 23 de febrero de 2016