Artículo original

Necesidad de superación en modelos matemáticos de epidemiología

Need for improvement in mathematical models of epidemiology

0000-0003-0043-9526José Aureliano Betancourt-Bethencourt^{1  *}  , 0000-0003-1971-3417Judith Aúcar-López²  , 0000-0001-7477-3127Marelys Cendra-Asencio³ 

¹ Universidad de Ciencias Médicas. Centro de Inmunología y Productos Biológicos. Camagüey, Cuba.

² Universidad de Ciencias Médicas. Departamento de Ciencia e Innovación Tecnológica. Camagüey, Cuba.

³ Dirección Provincial de Salud Pública. Camagüey, Cuba.

RESUMEN

Introducción:

En Cuba, se formulan modelos matemáticos, pero no están contemplados para la superación de posgrado ni en pregrado. Aunque los modelos idealizan la realidad, permiten, de manera sencilla, hacer predicciones sobre el comportamiento futuro de una enfermedad y tomar las medidas necesarias.

Objetivo:

Identificar necesidad de superación en modelos matemáticos de epidemiología.

Métodos:

Se utilizó un modelo estocástico presente en el paquete EpiModel del programa R. Se simularon tres situaciones diferentes, la primera con violaciones del distanciamiento y la higiene general, la segunda con mejoras en estos dos aspectos, más la inmunidad lograda al 70 % de la población por vacunación y la tercera con mejoras notables en higiene y distanciamiento junto a la vacunación. Se calculó, además, el comportamiento del número reproductivo con el paquete earlyR a partir de la incidencia.

Resultados:

Se valoró como las trayectorias con los modelos estocásticos tienen más variabilidad y como la reducción de contactos aplana la curva. Se evaluó la dispersión de la epidemia en situaciones de violaciones de la prevención y en otras donde hay prevención y además vacunación. La línea roja de cada modelo varía según las circunstancias, claramente en los casos de violaciones de distanciamiento e higiene esta curva se amplia y se aplana en el caso contrario.

Conclusiones:

Se identificaron suficientes evidencias sobre el uso y la necesidad de modelos matemáticos para apoyar la toma de decisiones en la epidemiología, se identificó la necesidad de superación en posgrado sobre la teoría de epidemias, que puede extenderse a pregrado.

Palabras-clave: CONCEPTOS MATEMÁTICOS; EPIDEMIOLOGÍA ANALÍTICA; MODELOS EPIDEMIOLÓGICOS; ESTUDIOS DE SERIES TEMPORALES; COVID-19

ABSTRACT

Introduction:

In Cuba mathematical models are formulated, but they are not contemplated for passing graduate or undergraduate degrees.

Objective:

To identify the need to work with mathematical simulations.

Methods:

A stochastic model present in the EpiModel package of the R program was used. Three different situations were simulated, the first with violations of distancing and general hygiene, the second with improvements in these two aspects, plus the immunity achieved to 70% of the population by vaccination and the third with notable improvements in hygiene and distancing together with vaccination. The behavior of the reproductive number with the early R package was also calculated from the incidence.

Results:

It is assessed how the trajectories with the stochastic models have more variability and how the reduction of contacts flattens the curve. The spread of the epidemic is valued in situations of prevention violations and in others where there is prevention and also vaccination.

Conclusions:

Sufficient evidence is presented on the use and need of mathematical models to support decision-making in epidemiology, the need to improve the theory of epidemics in graduate school is identified, which can be extended to undergraduate.

Key words: MATHEMATICAL CONCEPTS; ANALYTICAL EPIDEMIOLOGY; EPIDEMIOLOGIC MODELS; TIME SERIES STUDIES; COVID-19

Introducción

En el ámbito cubano, se formulan de manera disciplinaria excelentes modelos matemáticos, pero estos no están contemplados para la superación de posgrado en los programas de la Universidad de Ciencias Médicas de Camagüey. Los estudiantes de medicina y los epidemiólogos de la provincia deberían trabajar por sí mismo con simulaciones para valorar el efecto de diferentes intervenciones durante la pandemia de COVID-19 o en futuros eventos.

La dinámica actual conlleva a aplicar teorías transdisciplinarias, por tanto, las universidades tienen el reto de liderar el proceso de transformación, al introducir cambios en los procesos formativos que permitan a los futuros profesionales en salud pública, encontrar en la transdisciplinariedad, una herramienta para fortalecer la investigación y el diálogo de saberes. ^1,2

Dado el impacto de la COVID-19, se manifiestan cambios en el uso de la inteligencia artificial, nuevas maneras de aprendizaje a distancia, consultas médicas a distancia y otros, lo que demuestra que para lograr resiliencia hay que fortalecerse en estos métodos adaptativos que requieren enfoques integradores. ^{( )}

La actual pandemia de COVID-19 tiene un alto componente social, de allí la necesidad de abordarla con una visión integradora, ^{( , )} y lograr resultados que produzcan impacto social. ^{( )}

El artículo tiene como objetivo identificar la necesidad de trabajar de manera transdisciplinaria con simulaciones para que se utilicen como herramientas con el fin de evaluar el efecto de diferentes intervenciones durante la pandemia de COVID-19 o en futuros eventos.

Métodos

En la Universidad de Ciencias Médicas de Camagüey se realizó durante julio de 2021 un estudio poblacional. Se utilizó una serie de tiempo de casos confirmados de COVID-19 de un municipio, con las que se calculó el comportamiento del número reproductivo con el paquete earlyR a partir de dicha incidencia.

Para evaluar la dinámica de dispersión de la enfermedad se utilizó un modelo estocástico (icm) presente en el paquete EpiModel, ^{( )} del programa R. ^{( )} Se simularon tres situaciones diferentes, la primera con violaciones del distanciamiento y la higiene general, la segunda con mejoras en estos dos aspectos, más la inmunidad lograda al 70 % de la población y la tercera con mejoras notables en higiene y distanciamiento junto a la vacunación.

Resultados

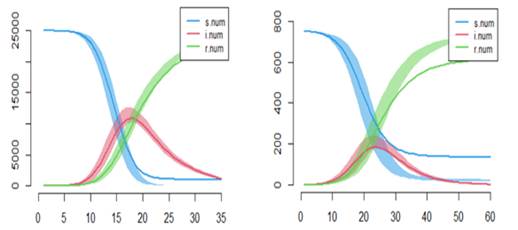
En la figura 1 a la izquierda las personas que han tenido diez contactos por día con un índice de transmisibilidad de 0,4 (enferman 4 de cada 100), lo que quiere decir que ni el distanciamiento ni las medidas higiénicas en general se cumplieron. En menos de 20 días hay un pico de enfermos de 10 000 personas.

A la derecha se logra distanciamiento y solo han tenido tres contactos del hogar además se redujo a la mitad la transmisibilidad, es decir que se doblaron las medidas generales de higiene (uso de nasobuco, lavado de manos y de superficies), pero además aquí la población total fue vacunada y se logra una inmunidad del 70 %. Aquí a los 25 días hay un pico de 200 personas enfermas (Figura 1).

Figura 1 Número de casos (y) por días (x).  

La línea roja es la trayectoria de los posibles infectados.

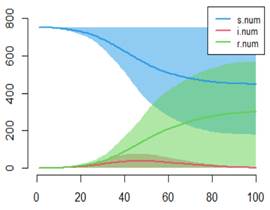
De manera que la situación que se presenta se puede controlar con cuarentena y aislamiento de los casos que se presenten. En la figura 2 se muestra el posible resultado con mejoras notables en la higiene, la vacunación y el distanciamiento. Se logra aplanar la curva y son mínimos y controlables los casos que se presentan (Figura 2).

Figura 2 Número de casos (y) por días (x).  

La línea roja es la trayectoria de los posibles infectados.

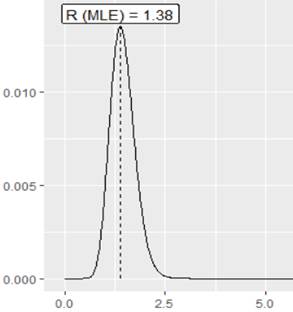
Se calculó además el comportamiento del número reproductivo con el paquete earlyR a partir de la incidencia, resultados que mostraron el comportamiento de brote epidémico R0>1 (Figura 3).

Figura 3 Probabilidad de distribución de R. 

Discusión

Abelló et al. ⁹ y Ortigoza et al., ¹⁰⁾ argumentan las posibilidades del uso del modelo Susceptible Infectado Recuperado (SIR básico) y políticas antiepidémicas de salud pública para la COVID-19 en Cuba, exponen su utilidad como modelo dinámico para hacer proyecciones en situaciones epidémicas que se aplican a regiones locales específicas y se manifiestan sus potencialidades para analizar rebrotes por la aparición de eventos locales que se alejan de las predicciones previstas.

Vargas et al. ¹¹ y Estrada et al., ¹² exponen las posibilidades existentes con el uso de estos modelos matemáticos, encontraron que el número de reproducción básico (R0) calculado permitió determinar que, para erradicar la pandemia por vacunación, la población inmunizada debe ser superior al 72 %.

De igual manera este tipo de modelos han sido utilizados por Amster P, ¹³ y Peralta et al., ¹⁴ mientras que Jiménez et al., ¹⁵⁾ utilizaron la modelación basada en agente; donde fue posible operacionalizar la manera en que distintas variables interactúan entre sí. Esto posibilita simular en un contexto multidimensional el efecto no lineal de variables explicativas sobre la evolución de la COVID-19. El aislamiento social fue en todos los casos, la medida que más incidió en el comportamiento de la difusión del virus, por lo tanto, la que más ayuda a la prevención y la ralentización del contagio.

Álvares et al., ¹⁶ con su modelo demuestran la eficacia de medidas no farmacéuticas, tales como el distanciamiento físico, aislamiento de casos, cuarentena domiciliaria, encierro total, la elección de las intervenciones o combinaciones más adecuadas para un territorio particular, dependerá en última instancia de las condiciones socioeconómicas y de salubridad, así como de una validación a gran escala de la viabilidad de los escenarios identificados de manera previa mediante la herramienta.

Se pretende que la tarea educativa sobre estos modelos se acentúe en la epidemiología matemática; a la economía matemática y financiera que explique el efecto y consecuencias múltiples de la pandemia, que evalúe el impacto de la pobreza, la migración y la desigualdad social. ^{( , )}

De acuerdo a Vidal et al., ¹⁹ la educación médica superior incorpora en los diferentes currículos de las carreras de ciencias médicas, el modelado de situaciones, según corresponda. Sin embargo, en casos de epidemias debe ponerse énfasis en estas herramientas científicas para el aprendizaje de modelos que permitan su pronóstico, seguimiento y control, como parte de la formación y aplicación en los diferentes escenarios docentes y de trabajo.

El estudio e interpretación de estas modelaciones no se encuentran incluidos en el plan de estudio de las diferentes carreras y especialidades de las ciencias médicas, en especial las de epidemiología, por lo que el equipo de investigación buscó apoyo en un grupo de expertos de la Universidad de Camagüey para la realización de los mismos con la utilización de la transdisciplina y el trabajo conjunto en aras de ofrecer esta valiosa información y vía de análisis para la toma de decisiones ante el impacto de la COVID-19 en la provincia Camagüey.

CONCLUSIONES

Se identifican evidencias sobre el uso y la necesidad de modelos matemáticos para apoyar la toma de decisiones en la epidemiología.

Se evidencia la necesidad de trabajar de manera transdisciplinaria con simulaciones para que las utilicen como herramientas con el fin de valorar el efecto de diferentes intervenciones durante la pandemia de COVID-19. Se introducen los modelos estocásticos que son más precisos que los deterministas. Se expone la necesidad de superación en posgrado sobre la teoría de epidemias, que puede extenderse a pregrado.

Referencias bibliográficas

1.  Castilla MÁ, Guerra MF, Villadiego EM. Salud pública: un campo de confrontación del paradigma disciplinar y transdisciplinar. Revista Avances En Salud [Internet]. 2018 [citado 06 Jul 2021];2(2):48-57. Disponible en: Disponible en: https://revistas.unicordoba.edu.co/index.php/avancesalud/article/view/1457 1.

2.  Más Bermejo P, Vidal Ledo MJ, Baldoquín Rodríguez W, Seuc Jo AH, Guinovart Díaz R, Pérez Rodríguez N, et al. Organización de la investigación epidemiológica para la lucha antiepidémica contra la COVID-19 en Cuba. INFODIR [Internet]. 2020 [citado 08 Jul 2021];32. Disponible en: Disponible en: http://revinfodir.sld.cu/index.php/infodir/article/view/831/1304 2.

3.  Nuno Martins P. A transdisciplinary perspective of the current crisis situation in the world. EPRA IJMR [Internet]. 2020 May [citado 08 Ago 2021];6(5):2455-3662. Disponible en: Disponible en: https://eprajournals.com/jpanel/upload/3.EPRA%20JOURNALS-4404.pdf 3.

4.  Moradian N, Ochs HD, Hamblin MR, Camargo CA, Martinez JA, Biamonte JD, et al. The urgent need for integrated science to fight COVID‑19 pandemic and beyond. J Transl Med [Internet]. 2020 [citado 12 Ago 2021];18:25. Disponible en: Disponible en: https://translational-medicine.biomedcentral.com/articles/10.1186/s12967-020-02364-2 4.

5.  Laupacis A. Working together to contain and manage COVID-19. CMAJ [Internet]. 2020 Mar [citado 15 Ago 2021];192(13):E340-1. Disponible en: Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7124162/ 5.  .

6.  Smetschka B, Gaube V. Co-creating formalized models: Participatory modelling as method and process in transdisciplinary research and its impact potentials. Environmental Science and Policy [Internet]. 2020 [citado 19 Ago 2021];103:41-49. Disponible en: Disponible en: https://enviro2.doe.gov.my/ekmc/wp-content/uploads/2020/07/Co-creating-formalized-models-Participatory-modelling-as-_2020_Environmenta.pdf 6.

7.  Jenness SM, Goodreau SM, Morris M. EpiModel: An R Package for Mathematical Modeling of Infectious Disease over Networks. J Stat Softw [Internet]. 2018 Abr [citado 19 Ago 2021];84:8. Disponible en: Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5931789/ 7.  .

8.  Core Team R. R: A language and environment for statistical computing. R Foundation for Statistical Computing [Internet]. Viena: GBIF; 2018 [citado 06 Ago 2021]. Disponible en: Disponible en: https://www.gbif.org/es/tool/81287/r-a-language-and-environment-for-statistical-computing 8.

9.  Abelló Ugalde IA, Guinovart Díaz R, Morales Lezca W. El modelo SIR básico y políticas antiepidémicas de salud pública para la COVID-19 en Cuba. Rev cuba salud pública [Internet]. 2020 [citado 09 Ago 2021];46(Suppl 1):e2597. Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S0864-34662020000500013 9.

10.  Ortigoza G, Lorandi A, Neri I. Simulación Numérica y Modelación Matemática de la propagación del Covid 19 en el estado de Veracruz. Rev Mex Med Forense [Internet]. 2020 [citado 06 Ago 2021];5(3):21-37. Disponible en: Disponible en: https://www.medigraphic.com/pdfs/forense/mmf-2020/mmf203c.pdf 10.

11.  Sánchez Vargas HE, Beltrán Ramos-Sánchez L, Galindo-Llanes PA, Salgado Rodríguez A. Modelación físico-matemática para la toma de decisiones frente a la COVID-19 en Cuba. Rev retos [Internet]. 2020 Jul-Dic [citado 06 Ago 2021];14(2):55-86. Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S2306-91552020000200054 11.

12.  Estrada Álvarez JM, Ospina Ramírez JJ, Hincapié Acuña M, Gómez González MP. Estimación del intervalo serial y número reproductivo básico para los casos importados de COVID-19. Rev salud pública [Internet]. 2020 Mar-Abr [citado 12 Ago 2021];22(2). Disponible en: Disponible en: http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0124-00642020000200214&lng=en&nrm=iso 12.

13.  Amster P. La matemática de las epidemias. Rev Educ Mat [Internet]. 2020 [citado 07 Ago 2021];35(2):5-20. Disponible en: Disponible en: https://revistas.unc.edu.ar/index.php/REM/article/view/29726 13.

14.  Peralta Polo J, Caro Candezano MA, Niebles Núñez L. Dos enfoques matemáticos epidemiológicos para modelar el comportamiento de los decesos causados por el CoViD-19. Investigación e Innovación en Ingenierías [Internet]. 2020 Jul-Dic [citado 14 Ago 2021];8(2). Disponible en: Disponible en: http://revistas.unisimon.edu.co/index.php/innovacioning/article/view/4257 14.

15.  Jiménez Romero C, Tisnés A, Linares S. Modelo de simulación del COVID-19 basado en agentes. Aplicación al caso argentino. POSICION [Internet]. 2020 [citado 17 Ago 2021];3. Disponible en: Disponible en: https://ri.unlu.edu.ar/xmlui/bitstream/handle/rediunlu/687/Jimenez%20Romero_COVID1-9.pdf?sequence=1&isAllowed=y 15.

16.  Álvares Pomar L, Rojas Galeano S. Herramienta basada en agentes para la valoración del impacto de intervenciones no farmacéuticas contra la COVID-19. TecnoL [Internet]. 2020 Sep-Dic [citado 09 Ago 2021];23(49). Disponible en: Disponible en: http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0123-77992020000300179 16.

17.  Mercado Sánchez GA. Las matemáticas en los tiempos del Coronavirus. Educación Matemática [Internet]. 2020 Abr [citado 19 Ago 2021];32(1):7-10. Disponible en: Disponible en: http://www.revista-educacion-matematica.org.mx/descargas/vol32/1/01REM32-1.pdf 17.

18.  Álvarez Mora D, Díaz Rodríguez IM, Flores Domínguez T, Peña Chávez M, Montero Ayala O. Modelos matemáticos aplicados a la Epidemiología. Multimed [Internet]. 2021 [citado 19 Ago 2021];25(1). Disponible en: Disponible en: http://www.revmultimed.sld.cu/index.php/mtm/article/view/1406/2150 18.

19.  Vidal Ledo M, Guinovart Díaz R, Baldoquín Rodríguez W, Valdivia Onega NC, Morales Lezca W. Modelos matemáticos para el control epidemiológico. Educ Med Super [Internet]. 2020 Abr-Jun [citado 22 Ago 2021];34(2). Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S0864-21412020000200026 19.

Recibido: 27 de Septiembre de 2021; Aprobado: 22 de Abril de 2022

^* Autor para la correspondencia (email): [e-mail]

Los autores declaran que no existen conflictos de intereses.

José Aureliano Betancourt-Bethencourt (Conceptualización. Análisis formal. Investigación. Metodología. Software. Supervisión. Visualización. Redacción).

Judith Aúcar-López (Curación de datos. Redacción).

Marelys Cendra-Asencio (Curación de datos. Redacción).