Artículo Original

La ecuación de onda como condición de frontera en un modelo de flujo en canales

The wave equation as a boundary condition in a channel flow model

Dr. David Ernesto Marón Domínguez¹  , Esp. Alberto Gutiérrez de la Rosa¹  , Dr. Emilio Ricardo Escartín Sauleda² 

¹CEMAT, Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), La Habana, Cuba.

²Depto. Geociencias, Facultad Ing. Civil, Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), La Habana, Cuba.

RESUMEN

Se muestra un modelo no estacionario formado por la ecuación diferencial hiperbólica 1D, el cual es utilizado en la práctica de la propagación de ondas en ríos y canales. Como condición de frontera aguas arriba se ha tomado una función que depende del tiempo representando la variación de los niveles del agua en el canal. Aguas abajo se toma como condición de frontera la ecuación de onda con primeras derivadas en el espacio y el tiempo, garantizando así que no exista reflexión de la onda en dicha frontera. Se formulan algoritmos numéricos obtenidos de la aplicación del Método de las Diferencias Finitas y del Método de los Elementos Finitos y se comparan los algoritmos de cálculo con una solución analítica mostrándose buenos resultados.

Palabras-clave: condiciones iniciales; condiciones de frontera; diferencias finitas; ecuación hiperbólica de orden dos; elementos finitos

ABSTRACT

A non-stationary model is shown, formed by the 1D hyperbolic differential equation, which is commonly used in practice for wave propagation of rivers and channels. As an upstream boundary condition, a function that depends on time has been taken, representing the variation of the water levels in the channel. Downstream, the wave equation with first derivatives in space and time is taken as the boundary condition, thus ensuring that there is no reflection of the wave in that boundary. Numerical algorithms obtained from the application of the Finite Differences Method and the Finite Element Method are formulated and the calculation algorithms are compared with an analytical solution showing good results.

Key words: initial conditions; boundary conditions; finite differences; hyperbolic equation of order two; finite elements

INTRODUCCIÓN

En muchos problemas de ingeniería es necesario resolver un modelo matemático conformado por una ecuación hiperbólica 1D no estacionaria, llamada ecuación de onda, conjuntamente con dos condiciones iniciales y dos condiciones de fronteras. Este tipo de ecuación diferencial es muy utilizada en ingeniería, en particular en hidráulica (^{Marón 2001}), geofísica, eléctrica, etc., en la modelación matemática de la propagación de ondas. Para el caso de un canal horizontal el modelo puede plantearse de la siguiente manera:

$\frac{{\partial }^{2}u}{\partial t^2}=c^2\frac{{\partial }^{2}u}{\partial x^2} 0<x<L, t>0$ (1)

donde: c es la velocidad de la onda en un canal, la cual viene definida por la expresión c ² = g H, g = 9,81 m/s² y H es el nivel de referencia del agua en el canal, u = u(x, t) es la función incógnita, la cual representa las variaciones de los niveles del agua en el canal respecto del nivel H, t es la variable temporal, x es la variable espacial, L es la longitud o tramo del canal simulado.

A la ecuación anterior hay que añadirle dos condiciones iniciales y dos condiciones de fronteras. Las condiciones iniciales pueden escribirse en la forma:

$u\left(x\mathrm{,0}\right)=s\left(x\right) y \frac{\partial u}{\partial t}\left(x\mathrm{,0}\right)=v\left(x\right)$ (2)

donde: s(x) y v(x)son funciones conocidas que pueden simular el desplazamiento inicial y la velocidad inicial, respectivamente, del movimiento del agua en el canal.

La condición de frontera en el extremo de la izquierda, aguas arriba x=0, se toma de tipo Dirichlet, es decir, de valores conocidos de los niveles del agua en el canal. Si en el extremo de la derecha, aguas abajo, se toma una condición de frontera de tipo Dirichlet o de tipo Neumann y se resuelve el modelo numéricamente, se obtiene que una parte de la onda se refleje en dicho extremo. Aquí el objetivo fundamental es encontrar una condición de frontera aguas abajo con la cual la onda transite por dicho extremo sin reflexión de la misma. Para lograr este objetivo se toma como condición de frontera aguas abajo la expresión definida en (3). Esta condición, en el extremo derecho x=L, se puede escribir de la forma siguiente:

$\frac{\partial u}{\partial t}\left(L,t\right)+c\frac{\partial u}{\partial x}\left(L,t\right)=0$ (3)

Al observar la condición de frontera anterior, se identifica que representa la evaluación, en x=L, de la ecuación diferencial de una onda que viaja hacia la derecha con velocidad $c$ . Esto se puede deducir de la propia ecuación (1), ya que el operador diferencial de la ecuación (1) se puede descomponer en la forma:

$\left(\frac{\partial }{\partial t}-c\frac{\partial }{\partial x}\right)\left(\frac{\partial }{\partial t}+c\frac{\partial }{\partial x}\right)u=0$ (4)

El primer factor de la ecuación (4) tiene como solución una onda que viaja hacia la izquierda con velocidad $–c$ . Teniendo en cuenta todo lo anterior, se ha formulado el siguiente modelo matemático:

$\left\{\begin{array}{c}\begin{array}{c}\frac{{\partial }^{2}u}{\partial t^2}=c^2\frac{{\partial }^{2}u}{\partial x^2} 0<x<L , t>0\\ u\left(x,0\right)=s\left(x\right) \frac{\partial u}{\partial t}\left(x,0\right)=v\left(x\right) t=0 , 0\le x\le L\end{array}\\ u\left(0,t\right)=p_0\left(t\right) x=0 , t>0\\ \frac{\partial u}{\partial t}\left(L,t\right)+c\frac{\partial u}{\partial x}\left(L,t\right)=0 x=L , t>0\end{array}\right.$ (5)

El objetivo de este trabajo es resolver este modelo de las ecuaciones (5) utilizando el Método de las Diferencias Finitas (MDF) y el Método de los Elementos Finitos (MEF) considerando la condición de frontera (3) y comparar los resultados obtenidos con una solución analítica para un caso particular. Se mostrará que con la condición de frontera que se ha tomado en el extremo aguas abajo $x=L$ no hay reflexión de la onda en dicho extremo.

EL MÉTODO DE LAS DIFERENCIAS FINITAS (MDF)

Esquemas explícitos

La aplicación del MDF a la ecuación diferencial del modelo (5) se realiza utilizando la fórmula de aproximación de tres puntos para las segundas derivadas (^{Samarski y Nikolaev 1982}), (^{Martínez 1990}), (^{Martínez 1999}), obteniéndose el siguiente esquema:

$\frac{u_i^{k-1}-2 u_i^k+u_i^{k+1}}{\Delta t^2}=c^2\left(\frac{u_{i-1}^k-2 u_i^k+u_{i+1}^k}{\Delta x^2}\right)$ (6)

Como se observa, el esquema anterior es explícito, de orden 2 en el espacio y en el tiempo, y se puede despejar y calcular el valor de $u_i^{k+1}$ en la ecuación anterior a partir de que sean conocidos los valores de $u_i^{k-1}$ y $u_i^k$ .

El índice $k$ indica el nivel de tiempo y varía desde $k=2$ hasta $N_t$ , el subíndice $i$ indica el nodo espacial y varía desde $i=2$ hasta $N_x$ . Aquí $N_t$ representa la cantidad de subintervalos de la partición de la malla en el tiempo, $N_x$ representa la cantidad de subintervalos de la partición de la malla en la dirección de $x$ ; $\Delta x$ y $\Delta t$ representan los incrementos en cada una de las variables independientes.

El despeje de $u_i^{k+1}$ en (6) conduce a la expresión:

$u_i^{k+1}=2 u_i^k-u_i^{k-1}+{\left(N{C}_r\right)}^2\left(u_{i-1}^k-2 u_i^k+u_{i+1}^k\right) ; N{C}_r=\frac{c \Delta t}{\Delta x}$ (7)

donde: $N{C}_r$ es el Número de Courant. En la literatura se le exige a este coeficiente que sea menor que 1 para que se garanticen las condiciones de estabilidad numérica y se evite el fenómeno de la dispersión numérica.

La discretización de la condición de frontera del extremo de la izquierda, $x=0$ se obtiene de la evaluación directa de la función que se tome en ese extremo, dada en (5), es decir,

$u_1^k=p_0\left(t_k\right) para k=\mathrm{2,3,}\dots \mathrm{.,}{N}_t+1$ (8)

La discretización de la condición de frontera del extremo de la derecha, $x=L$ dada en (5), se obtiene utilizando la fórmula centrada para la derivada en el espacio, lo cual hace que aparezca el nodo ficticio en el espacio $i=N_x+2$ .

Para la derivada en el tiempo se utiliza una fórmula centrada, obteniéndose una aproximación para el valor de la función incógnita en el nodo $i=N_x+1$ para el nivel de tiempo $k+1$ con la ayuda de la expresión siguiente:

$u_{N_x+1}^{k+1}=(\left(2-2{\left(N{C}_r\right)}^2) u_{N_x+1}^k+2{\left(N{C}_r\right)}^2{u}_{N_x}^k+\left(N{C}_r-1\right)u_{N_x+1}^{k-1}\right)/\left(1+N{C}_r\right)$ (9)

Para la discretización de la condición inicial asociada con la velocidad, dada en (5), se utiliza una fórmula centrada en el tiempo. En este caso aparece el llamado nodo ficticio en el tiempo $k=0$ . De esta forma se obtiene una aproximación para calcular los valores de la función incógnita en el nivel de tiempo $k=2$ según la expresión:

$u_i^2=u_i^1+\Delta t v\left(x_i\right)+0.5 {\left(N{C}_r\right)}^2\left(u_{i-1}^1-2 u_i^1+u_{i+1}^1\right)$ (10)

El término $u_i^1$ que aparece en la expresión anterior se obtiene de la discretización de la primera condición inicial de (5) según la evaluación directa del desplazamiento:

$u_i^1=S\left(x_i\right) para i=\mathrm{2,} \mathrm{3,}\dots ,N_x+1$ (11)

Si se evalúa la expresión (9) en $k=1$ se utiliza lo referido al nodo ficticio en el tiempo $k=0$ y se obtiene una expresión con la que se pueden determinar los valores de la función incógnita en el nodo frontera $i=N_x+1$ para el nivel de tiempo $k=2$ :

$u_{Nx+1}^2=\left(1-{\left(N{C}_r\right)}^2\right)u_{Nx+1}^1+{\left(N{C}_r\right)}^2{u}_{Nx}^1+\left(1-N{C}_r\right)\Delta t v\left(x_{Nx+1}\right)$ (12)

Finalmente, el modelo numérico en diferencias finitas que hay que resolver se puede resumir por las siguientes ecuaciones en diferencias finitas:

$u_i^1=S\left(x_i\right) \left(11\right)$

$u_1^k=p_0\left(t_k\right) \left(8\right)$

$u_i^2=u_i^1+\Delta t v\left(x_i\right)+\mathrm{0,5}{\left(N{C}_r\right)}^2\left(u_{i-1}^1-2u_i^1+u_{i+1}^1\right) \left(10\right)$

$u_{Nx+1}^2=\left(1-{\left(N{C}_r\right)}^2\right)u_{Nx+1}^1+{\left(N{C}_r\right)}^2{u}_{Nx}^1+\left(1-N{C}_r\right)\Delta t v\left(x_{Nx+1}\right) \left(12\right)$

$u_i^{k+1}=2u_i^k-u_i^{k-1}+{\left(N{C}_r\right)}^2\left(u_{i-1}^k-2u_i^k+u_{i+1}^k\right) \left(7\right)$

$u_{Nx+1}^{k+1}=\frac{\left(2-2{\left(N{C}_r\right)}^2\right)u_{Nx+1}^k+2{\left(N{C}_r\right)}^2{u}_{Nx}^k+\left(N{C}_r-1\right)u_{Nx+1}^{k-1}}{1+N{C}_r} \left(9\right)$

Luego el conjunto de ecuaciones anteriores conforman el modelo numérico de las ecuaciones (5), que corresponde a un esquema explícito de orden dos. En el proceso de discretización de la segunda derivada con respecto a la variable espacial que aparece en la ecuación diferencial del modelo (5) se puede aplicar también un operador de orden cuatro que tiene la forma:

$\frac{{\partial }^{2}u}{\partial x^2}\left(x_i,t_k\right)\approx \frac{-u_{i-2}^k+16 u_{i-1}^k-30 u_i^k+16 u_{i+1}^k-u_{i+2}^k}{12 \Delta x^2}$ (13)

Por lo tanto, sustituyendo (13) en el miembro de la derecha de (6) se obtiene:

$\frac{u_i^{k-1}-2 u_i^k+u_i^{k+1}}{\Delta t^2}=c^2\left(\frac{- u_{i-2}^k+16 u_{i-1}^k-30 u_i^k+16 u_{i+1}^k-u_{i+2}^k}{12 \Delta x^2}\right)$ (14)

De forma similar a todo lo realizado para obtener el modelo numérico de orden dos, se puede llegar a obtener un modelo numérico de orden cuatro con ayuda de (14) según ^{Espinoza y Niño (2001}).

MDF Esquema implícito

El modelo (5) también se puede discretizar con un esquema implícito (^{Montenegro y Díaz 1987}), (^{Dong 2006}). Este se obtiene si la segunda derivada con respecto a la variable espacial que aparece en la ecuación diferencial se discretiza según el siguiente operador en diferencias finitas:

$\frac{{\partial }^{2}u}{\partial x^2}\left(x_i,t_k\right)\approx \frac{u_{i-1}^{k-1}-2{ u}_i^{k-1}+u_{i+1}^{k-1}}{4{ ∆x}^2}+2\frac{u_{i-1}^k-2 u_i^k+u_{i+1}^k}{4{ ∆x}^2}+\frac{u_{i-1}^{k+1}-2 u_i^{k+1}+u_{i+1}^{k+1}}{4 {∆x}^2}$ (15)

Sustituyendo (15) en el miembro de la derecha de (6) y agrupando convenientemente se obtiene el siguiente esquema en diferencias finitas:

$a_i{u}_{i-1}^{k+1}+b_i{u}_i^{k+1}+c_i{u}_{i+1}^{k+1}=d_i$ (16)

donde los coeficientes del esquema anterior vienen dados por:

$\begin{array}{c}{a}_i=-{\left(N{C}_r\right)}^2\\ b_i=\left(4+2{\left(N{C}_r\right)}^2\right)\\ \begin{array}{c}{c}_i=-{\left(N{C}_r\right)}^2\\ d_i=4\left(2u_i^k-u_i^{k-1}\right)+{\left(N{C}_r\right)}^2\left(u_{i+1}^{k-1}-2u_i^{k-1}+u_{i+1}^{k-1}+2\left(u_{i+1}^k-2u_i^k+u_{i+1}^k\right)\right)\end{array}\end{array}$ (17)

Según se observa en (16) y (17), el esquema anterior se corresponde con un sistema de ecuaciones algebraicas lineales, el cual tiene una matriz tridiagonal.

Los valores de las incógnitas corresponden al nivel de tiempo $k+1$ y los valores conocidos corresponden a los niveles de tiempo $k y k-1$ , los cuales forman parte de los términos independientes del sistema. A diferencia de los esquemas explícitos, en (16) hay que resolver este sistema de ecuaciones lineales para poder obtener los valores de las incógnitas.

EL MÉTODO DE LOS ELEMENTOS FINITOS (MEF)

Para poder comparar los resultados con el MDF aquí en el MEF se toma el elemento finito lineal, es decir, se utiliza la interpolación lineal por tramos. Se parte de la aplicación del Método de los Residuos Ponderados y se selecciona la variante de Galerkin donde las funciones de peso o de ponderación se seleccionan iguales a las funciones bases o coordenadas que definen a la función incógnita dentro de cada elemento.

La aplicación del Método de los Residuos Ponderados conduce a la expresión:

$\underset{0}{\overset{L}{{\displaystyle \int }}}\left(\frac{{\partial }^{2}u}{\partial t^2}-c^2\frac{{\partial }^{2}u}{\partial x^2}\right)M_i\left(x\right)dx=0 para i=\mathrm{1,2,}\dots ,N_x+1$ (18)

donde: $M_i\left(x\right)$ son las funciones de peso o de ponderación del nodo $i$ de la malla.

Después de separar las integrales e integral por partes en la integral que tiene la segunda derivada en el espacio se obtiene:

$\underset{0}{\overset{L}{{\displaystyle \int }}}\frac{{\partial }^{2}u}{\partial t^2}{M}_i\left(x\right)dx-c^2\left[M_i\left(L\right)\frac{\partial u}{\partial x}\left(L\right)-M_i\left(0\right)\frac{\partial u}{\partial x}\left(0\right)\right]+c^2\underset{0}{\overset{L}{{\displaystyle \int }}}\frac{\partial u}{\partial x}\frac{d{M}_i\left(x\right)}{dx}dx=0$ (19)

Como aguas arriba, en $x=0$ , hay condición de frontera de Dirichlet entonces el término correspondiente a la evaluación en $x=0$ que aparece dentro del corchete tiene que anularse.

Esto se garantiza tomando las funciones $M_i\left(x\right)$ correspondientes a los nodos $i=\mathrm{2,3,}\dots N_x+1$ , es decir, no tomando la función correspondiente al nodo $i=1$ . Por otra parte aguas abajo, en $x=L$ , está la condición de frontera (3) que corresponde a la ecuación de onda con primeras derivadas en el espacio y en el tiempo. Esta condición (3) se sustituye en (19) y se obtiene:

$c^2\underset{0}{\overset{L}{{\displaystyle \int }}}\frac{\partial u}{\partial x}\frac{d{M}_i\left(x\right)}{dx}dx+\underset{0}{\overset{L}{{\displaystyle \int }}}\frac{{\partial }^{2}u}{\partial t^2}{M}_i\left(x\right)dx+c{M}_i\left(L\right)\frac{\partial u}{\partial t}\left(L\right)=0$ (20)

Considerando a un elemento finito o subintervalo $R_e=\left[x_1,x_2\right]$ se tiene:

${\displaystyle \sum }_{e=1}^{N_x}\left(\left\{I_1^e\right\}+\left\{I_2^e\right\}\right)+\left\{I_3\right\}=\left\{0\right\}$ (21)

donde las componentes de cada expresión vectorial de (21) se calculan por:

$\left\{\begin{array}{c}{I}_{1i}^e=c^2\underset{R_e}{\overset{}{\int }}\frac{\partial u}{\partial x}\frac{d{M}_i\left(x\right)}{dx}dx para i=\mathrm{1,2} \\ I_{2i}^e=\underset{R_e}{\overset{}{\int }}\frac{{\partial }^{2}u}{\partial t^2}{M}_i\left(x\right)dx para i=\mathrm{1,2}\\ I_{3i}=c{M}_i\left(L\right)\frac{\partial u}{\partial t}\left(L\right) para i=\mathrm{1,2},\dots N_x+1\end{array}\right.$ (22)

Para calcular las dos primeras integrales se hace uso de la interpolación lineal por tramos de Lagrange lo cual permite escribir a la función incógnita $u^e\left(x\right)$ dentro del elemento finito $R_e$ en la forma:

$u^e\left(x,t\right)=u_1\left(t\right)L_1\left(x\right)+u_2\left(t\right)L_2\left(x\right)={\displaystyle \sum }_{j=1}^2{u}_j\left(t\right)L_j\left(x\right)$ (23)

donde: las funciones $u_1\left(t\right)$ y $u_2\left(t\right)$ representan las variaciones en el tiempo de los niveles del agua en los extremos del elemento finito o subintervalo; los polinomios $L_1\left(x\right)$ y $L_2\left(x\right)$ son los polinomios de interpolación lineal de Lagrange en el intervalo $\left[x_1, x_2\right]$ que interpolan a los valores $0 y 1$ y corresponden a las llamadas funciones bases o coordenadas.

Aquí se toman las funciones de peso o de ponderación iguales a las funciones bases o coordenadas, es decir $M_i\left(x\right)=L_i\left(x\right)$ , con lo cual se ha seleccionado la variante de Galerkin dentro del Método de los Residuos Ponderados.

Teniendo en cuenta todo lo anterior y sustituyendo (23) en las dos primeras integrales de (22) se llega a las expresiones matriciales y vectoriales siguientes como resultados del cálculo de ambas integrales.

$\left\{\begin{array}{c}\left\{I_1^e\right\}=\frac{c^2}{∆x}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right]\left\{u^e\right\}=\frac{c^2}{∆x}\left[A\right]\left\{u^e\right\}\\ \left\{I_2^e\right\}=\frac{∆x}{6}\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]\frac{{\partial }^2\left\{u^e\right\}}{\partial t^2}=\frac{∆x}{6}\left[B\right]\frac{{\partial }^2\left\{u^e\right\}}{\partial t^2}\end{array}\right.$ (24)

Como se observa en las expresiones anteriores las matrices $\left[A\right] y \left[B\right]$ son constantes de orden dos y los vectores $\left\{u^e\right\}$ se corresponden con los dos valores de la función incógnita en el elemento.

Al aplicar el MEF desaparece explícitamente la presencia de la variable espacial pero se observa la presencia del tiempo lo que quiere decir que las ecuaciones (24) son expresiones que dependen del tiempo. Por lo tanto, después que se aplicó el MEF en el espacio hay que aplicar el MDF en el tiempo.

Por otra parte, dichas expresiones (24) dependen de la malla de la región y de los coeficientes de la ecuación diferencial. Si la malla no es uniforme entonces el valor de $\Delta x$ no es constante en cada elemento representado en (24) y si los coeficientes de la ecuación diferencial no son constantes es porque el medio no es homogéneo lo cual significa que existe heterogeneidad del medio.

En ambos casos la expresión (24) es muy útil para simular situaciones de este tipo, lo que quiere decir que, aunque este problema de contorno es 1D, la aplicación del MEF demuestra que es mucho más general que el MDF y que a su vez es más fácil de implementar computacionalmente.

La última expresión de (22) representa un vector columna donde todas sus componentes son nulas excepto la última correspondiente al nodo frontera $i=N_x+1$ y cuya expresión es:

$\left\{I_3\right\}=c\frac{\partial u}{\partial t}\left(L\right){\left(\mathrm{0,0,}\dots \mathrm{,1}\right)}^T$ (25)

Sustituyendo las expresiones (24) y (25) en (21) y efectuando el ensamblaje sobre todos los elementos de la malla se obtiene un sistema de ecuaciones diferenciales ordinarias que depende del tiempo. A dicho sistema se le aplica el Método de las Diferencias Finitas y se obtiene el sistema de ecuaciones lineales

${\displaystyle \sum }_{e=1}^{N_x}\frac{\Delta x}{6\Delta t^2}\left[B\right]\left\{u^{e^{k+1}}\right\}={\displaystyle \sum }_{e=1}^{N_x}\left\{\frac{-c^2}{\Delta x}\left[A\right]\left\{u^{e^k}\right\}+\frac{\Delta x}{6\Delta t^2}\left[B\right]\left(2\left\{u^{e^k}\right\}-\left\{u^{e^{k-1}}\right\}\right)\right\}-\left\{I_3\right\}$ (26)

Como se observa en (26) aparecen los vectores $\left\{u^{e^{k+1}}\right\},\left\{u^{e^k}\right\} y \left\{u^{e^{k-1}}\right\}$ , por lo tanto (26) representa un esquema de tres tiempos cuyas incógnitas son las que corresponden con el tiempo $k+1$ y los demás valores en $k y k-1$ son conocidos. Para discretizar la expresión de $\left\{I_3\right\}$ se hace uso de la fórmula centrada en el tiempo con lo cual se obtiene:

$\left\{I_3\right\}=\frac{c}{2\Delta t}\left(u_{N_x+1}^{k+1}-u_{N_x+1}^{k-1}\right)$ (27)

El primer término de (27) tiene la presencia de un valor incógnita en el tiempo $k+1$ el cual se ensambla en el miembro izquierdo de (26) y el segundo término de (27) tiene la presencia de un valor conocido en el tiempo $k-1$ el cual se ensambla en el miembro derecho de (26).

Con respecto a las condiciones iniciales es necesario observar que para discretizar la segunda condición inicial es necesario aplicar el concepto de nodo ficticio en el tiempo. Se comienza discretizando la primera condición inicial de (5) según la forma:

$u\left(x\mathrm{,0}\right)=S\left(x\right) \to u_i^1=S\left(x_i\right) para i=\mathrm{1,2,3,}\dots ,N_x+1$ (28)

Recordar que aquí la función $S\left(x\right)$ representa el desplazamiento inicial de los niveles del agua en el canal, por lo tanto (28) no es una aproximación sino es una evaluación exacta. Luego con (28) ya se tienen todos los valores exactos de la función incógnita en el tiempo inicial $t=0$ lo cual corresponde con el primer nivel de tiempo $k=1$ .

Para la segunda condición inicial de (5) que tiene la presencia de la función $V\left(x\right)$ la cual representa la velocidad inicial de los niveles del agua en el canal, se aplica la fórmula centrada en el tiempo y se obtiene la expresión siguiente en la cual aparece el valor de la función incógnita $u_i^0$ en el nivel de tiempo $k=0$ el cual es precisamente el nodo ficticio mencionado:

$\frac{\partial u}{\partial t}\left(x\mathrm{,0}\right)=V\left(x\right) \to u_i^0=u_i^2-2\Delta t V\left(x_i\right) para i=\mathrm{1,2,3,}\dots ,N_x+1$ (29)

Por supuesto que la presencia de este nodo ficticio $k=0$ , en el tiempo hay que eliminarla de la formulación del algoritmo de cálculo. Para esto se evalúa el esquema (26) en el nivel de tiempo $k=1$ y se obtiene una expresión donde aparece el valor de la función incógnita $u_i^0$ .

Para eliminar este valor se sustituye la expresión (29) y finalmente se obtiene un sistema de ecuaciones que solo tiene la presencia de los valores de la función incógnita en los niveles de tiempo $k=1 y k=2$ , como se muestra en el siguiente sistema:

$\sum _{e=1}^{N_x}\frac{∆x}{3∆t^2}\left[B\right]\left\{u^{e^2}\right\}=\sum _{e=1}^{N_x}\left\{\frac{-c^2}{∆x}\left[A\right]\left\{u^{e^1}\right\}+\frac{∆x}{3∆t^2}\left[B\right]\left(\left\{u^{e^1}\right\}+∆t\left\{V\right\}\right)\right\}-cV\left(x_{N_x+1}\right){\left(\mathrm{0,0},\dots ,N_x+1\right)}^T$ (30)

Es bueno hacer notar en (30) la presencia de la función velocidad inicial $V\left(x\right)$ , de esta forma en (28) interviene $S\left(x\right)$ y en (30) interviene $V\left(x\right)$ las cuales son ambas datos del problema. Por lo tanto, después de resolver el sistema de ecuaciones (30) entonces ya se tienen los valores de la función incógnita $\left\{u^2\right\}$ en el nivel de tiempo $k=2$ . A partir de aquí y con el esquema (26) se pueden calcular los valores de la función incógnita en todos los restantes niveles de tiempos hasta el nivel de tiempo final.

COMPROBACIÓN DE LOS ALGORITMOS DE CÁLCULO

Todos los algoritmos de cálculo fueron implementados en el asistente matemático MATLAB y se muestra la comparación de los resultados de los algoritmos con una solución analítica para el caso en que se parte del reposo, de forma que las dos condiciones iniciales en (5) se toman nulas $S\left(x\right)=V\left(x\right)=0$ . Para la condición de frontera en $x=0$ , se ha tomado la siguiente función de tipo trigonométrica para representar las variaciones de los niveles del agua en dicha frontera aguas arriba:

$p_0\left(t\right)=A sen\left(wt\right) donde w=2\pi /T_t$ (31)

donde: A, w y T _t representan la semiamplitud, la frecuencia y el período de las oscilaciones de los niveles en dicha frontera, respectivamente.

Para estas suposiciones el modelo matemático (5) se reduce a la forma:

$\left\{ \begin{array}{c}\begin{array}{c}\frac{{\partial }^{2}u}{\partial t^2}=c^2\frac{{\partial }^{2}u}{\partial x^2} 0<x<L , t>0\\ u\left(x,0\right)=0 \frac{\partial u}{\partial t}\left(x,0\right)=0 t=0 , 0\le x\le L\end{array}\\ u\left(0,t\right)= A sen\left(w t\right) x=0 , t>0\\ \frac{\partial u}{\partial t}\left(L,t\right)+c\frac{\partial u}{\partial x}\left(L,t\right)=0 x=L , t>0 \end{array}\right.$ (32)

Si se aplica la Transformada de Laplace al modelo matemático anterior, se obtiene la solución exacta:

$U_e\left(x,t\right)=\left\{\begin{array}{c}A sen\left(w \left(t- x/c\right)\right) 0\le x\le c t\\ 0 x>c t \end{array}\right.$ (33)

Según se observa, la solución exacta (33) representa una onda en forma de una función seno que se mueve de izquierda a derecha con velocidad $c$ . Para efectuar la comprobación numérica se toma el siguiente juego de datos:

• c=1 m/s Velocidad de la onda en el canal

• L=160 m Longitud del canal

• N _x =32 Número de subintervalos en x

• T _f = 300 s Tiempo final de simulación

• N _t =150 Número de subintervalos en t

• A=1 amplitud de las oscilaciones en x=0

• T _t =80 s Período de las oscilaciones en x=0

El incremento en $x$ es $\Delta x=5 m$ , el incremento en $t$ es $\Delta t=2 s$ y el Número de Courant tiene el valor $N{C}_r=\mathrm{0,4}$ . A continuación se muestran los resultados numéricos y los gráficos de los algoritmos de cálculo correspondientes al MDF y al MEF. Se ha calculado el Máximo Error Absoluto $\left(\text{MaxErrAbs}\right)$ entre la solución aproximada $\left(U_a\right)$ y la solución exacta $\left(U_e\right)$ , para todos los nodos y todos los tiempos, según la expresión:

$MaxErrAbs=\max \left(\left|u_e-u_a\right|\right)$ (34)

En la tabla 1 siguiente se muestran los Máximos Errores Absolutos calculados según (34) con la solución exacta dada en (33) y los cuatro algoritmos desarrollados.

Tabla 1 Máximos Errores Absolutos entre $u_a \text{y} u_e$ para los diferentes esquemas 

Esquema explícito de orden cuatro (en m)	Esquema explícito de orden dos (en m)	Esquema implícito (en m)	MEF lineal (en m)
0,10	0,14	0,18	0,23

Para este ejemplo el esquema explícito de orden cuatro y el esquema explícito de orden dos tienen errores del mismo orden con una diferencia de 4 cm. El esquema implícito y el MEF tienen errores del mismo orden con una diferencia de 5 cm. A su vez estos dos últimos algoritmos tienen un error algo mayor que los dos explícitos. En todos los casos se observan los buenos ajustes alcanzados.

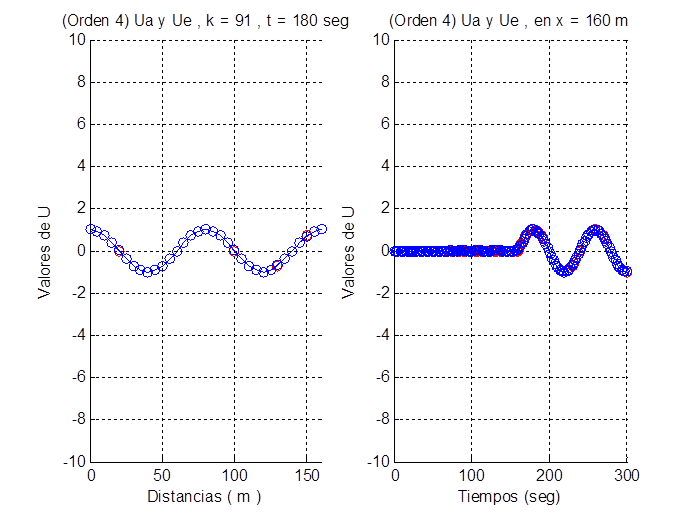
En la gráfica de la izquierda de cada una de las figuras 1, 2, 3 y 4, que se muestran a continuación, están representadas la solución aproximada $u_a$ y la solución exacta $u_e$ para cada uno de los cuatro algoritmos y para el tiempo $t=180 s$ que se corresponde con el nivel de tiempo $k=91$ .

En la gráfica de la derecha de cada una de las figuras se han representado las gráficas de $u_a$ y de $u_e$ en la frontera derecha, aguas abajo, correspondiente a la distancia $x=L=160 m$ .

Para el juego de datos seleccionado en este ejemplo se cumple que la longitud de onda es igual a 80 m que coincide con el producto de la velocidad $c$ de la onda por el periodo de las oscilaciones de los niveles del agua en el extremo aguas arriba. Esto se observa en la gráfica de la izquierda de las cuatro figuras ya que en la misma varía la distancia pero el tiempo está fijo.

En las cuatro figuras se observa además el buen ajuste alcanzado entre los valores calculados y los valores exactos.

Figura 1 Gráfica de $u_a y u_e$ del esquema de orden dos para $t=180 s$ (izquierda) y gráfica de $u_a y u_e$ en la frontera derecha $x=160 m$ (derecha) 

Figura 2 Gráfica de $u_a y u_e$ del esquema de orden 4 para $t=180 s$ (izquierda) y gráfica de $u_a y u_e$ en la frontera derecha $x=160 m$ (derecha) 

En la gráfica de la derecha de las cuatro figuras ocurre lo contrario, en el sentido de que varía el tiempo pero la posición está fija y dicha posición corresponde con el extremo de la derecha o aguas abajo, es decir $\text{x}=\text{L}=160\text{m}.$

Esto permite observar la llegada de la onda y su paso por dicha frontera. Aproximadamente durante los primeros 160 segundos la onda no ha llegado al extremo aguas abajo.

La onda comienza a pasar por dicha frontera desde los 160 $s$ hasta que se alcanza el tiempo final de simulación $300\text{s}$ . En las gráficas de la derecha se observa que, para ninguno de los cuatro algoritmos numéricos desarrollados, hay reflexión de la onda en dicha frontera ya que la solución numérica tiene un comportamiento similar a la solución exacta.

Figura 3 Gráfica de $u_a y u_e$ del esquema implícito para $t=180 s$ (izquierda) y gráfica de $u_a y u_e$ en la frontera derecha $x=160 m$ (derecha) 

Figura 4 Gráfica de $u_a y u_e$ del MEF para $t=180 s$ (izquierda) y gráfica de $u_a y u_e$ en la frontera derecha $x=160 m$ (derecha) 

Se calculó el Número de Courant y se obtuvo $N{C}_r=\mathrm{0,4}$ para todos los esquemas. Este valor cumple con la condición de estabilidad numérica reportada en la literatura que plantea que el Número de Courant en este tipo de modelo de flujo en canales debe de tener un valor menor que 1.

CONCLUSIONES

• Se confeccionaron tres algoritmos numéricos como resultado de la aplicación del MDF y un algoritmo como resultado del MEF al modelo matemático planteado con la ecuación hiperbólica de onda 1D. En el MDF se obtuvieron dos esquemas explícitos, uno de orden dos y el otro de orden cuatro y se obtuvo también un esquema implícito.

• La utilización de la ecuación de onda como condición de frontera en el extremo de la derecha, aguas abajo, demostró que como resultado de la solución numérica no se obtuvo reflexión de la onda en dicha frontera.

• Se implementaron todos los algoritmos de cálculo en el asistente matemático MATLAB y para un caso particular de simulación del que se dispone de solución analítica se pudo comparar la solución numérica obtenida de los algoritmos y la solución analítica mostrándose muy buenos resultados numéricos y gráficos.

REFERENCIAS

Dong S. (2006). “Finite difference methods for the hyperbolic wave partial differential equations”, 18.086 - Computational Science and Engineering II (Spring 2014), Dept. of Mathematics, Massachusetts Institute of Technology, USA.

Espinoza C. y Niño Y. (2001). “Métodos de diferencias finitas”, CI71D Modelación Numérica en Ingeniería Hidráulica y Ambiental, Centro Tecnológico Ucampus, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Chile.

Marón D. E. (2001). “Aplicación del MEF y del MDF en modelos de flujo y de transporte de contaminantes con densidad constante o variable en medios porosos saturados”, Tesis en opción al grado científico de Doctor en Ciencias Técnicas, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana.

Martínez J. B. (1990). “Simulación matemática de cuencas subterráneas: flujo impermanente bidimensional”, Imprenta ISPJAE, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana.

Martínez Y. (1999). “Solución de las ecuaciones de flujo para régimen impermanente unidimensional por los métodos de las diferencias finitas y de los elementos finitos”, Tesis de Maestría en Ingeniería Hidráulica, CIH, Instituto Superior Politécnico José Antonio Echeverría (Cujae), Habana.

Montenegro A. G. y Díaz L. A. (1987). “Métodos numéricos del algebra lineal”, Editorial Academia, La Habana.

Samarski A. A. y Nikolaev E.S. (1982). “Métodos de solución de las ecuaciones reticulares”, Editorial Mir, Moscú.

Recibido: 27 de Agosto de 2018; Aprobado: 12 de Junio de 2019

Dr. David Ernesto Marón Domínguez. CEMAT, Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), Habana. email: [e-mail]

Esp. Alberto Gutiérrez de la Rosa. CEMAT, Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), Habana. email: [e-mail]

Dr. Emilio Ricardo Escartín Sauleda. Depto. Geociencias, Facultad Ing. Civil, Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), Habana. email: [e-mail]