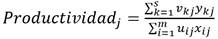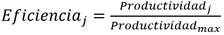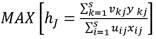Introducción
La agricultura de regadío consume alrededor del 70% del agua utilizada para usos consuntivos, la cual es gestionada de manera deficiente. “Eficiencia” en la gestión debe ser la palabra clave para los administradores de riego. Se requiere eficiencia en todas sus operaciones para que la sustracción de agua del subsuelo se mantenga en un mínimo, se puedan mantener ríos y mantos freáticos para el ambiente y el agua se entregue donde, cuando y en la cantidad requerida (Altamirano et al. 2019).
La mayoría de los sistemas de regadío del mundo están funcionando por debajo de su capacidad y no se ajustan a las necesidades de la agricultura actual (Olmedo 2017). El bajo nivel de productividad del agua asociado a la gestión de estos sistemas conlleva menores oportunidades de usar eficazmente los recursos y obtener rendimientos económicos.
Cuba no está ajena a esta situación, según Cisneros et al. (2011) haciendo referencia a Alemán et al. (2003) la baja eficiencia en la operación de los sistemas de riego constituye uno de los problemas más agudos que afectan a las áreas bajo riego, no basta con seguir instalando nuevos sistemas de riego cada año, sin alcanzar un nivel mínimo de eficiencia en el área bajo riego actual (González et al. 2004). Por tal razón, toda metodología o recomendación dirigida a la optimización en el aprovechamiento de los recursos hídricos y a la preservación del medio ambiente, adquiere un valor inmenso para las zonas bajo riego.
Dada la importancia del riego en la producción de alimentos, el alto porcentaje de agua utilizado en la agricultura y los problemas relacionados con su gestión, resulta pertinente estudiar el riego en Cuba desde un marco integral, con un enfoque en la eficiencia de sus sistemas operadores como entes ya sean productivos o de servicio.
En Cuba, desde el 2020 se ha retomado con gran fuerza el concepto de eficiencia en todos los sectores de la economía. Hoy en día, en el marco de un proceso de recuperación económica tras la pandemia de COVID-19, la tendencia al incremento en la asignación de recursos al sector agrícola se mantiene, con lo que se refuerza la importancia de velar por la eficiencia en este sector. Sin embargo, existen en el país pocas evidencias acerca de la eficiencia que alcanzan las áreas bajo riego, debido a ello el conocimiento y la aplicación de técnicas de evaluación de la relación recursos-resultados resulta de singular importancia.
El concepto de eficiencia, aplicado a las áreas de riego en Cuba, implicaría que éstas obtengan una determinada producción agrícola minimizando el consumo de recursos como agua, mano de obra, insumos, etc. Un área de riego será considerada relativamente eficiente si no existe ninguna otra tecnológicamente similar en la muestra que obtenga el mismo valor de la producción bruta utilizando menos de algún factor productivo y no más de los restantes (eficiencia en términos de inputs o entradas). Por tanto, una mejor gestión del regadío, por lo general, requeriría introducir políticas destinadas al aumento de la eficiencia de los inputs, entre ellos principalmente el agua, puesto que "se puede lograr más con menos agua" a través de una mejor gestión.
Un método apropiado para evaluar la eficiencia productiva de las áreas de riego es el método de análisis de envolvente de datos (DEA, por sus siglas en inglés). La metodología DEA, es utilizada para evaluar la eficiencia relativa de un conjunto de unidades productivas, utilizando un procedimiento no paramétrico que maneja una técnica de programación lineal. Con una serie de entradas (inputs) y salidas (outputs) para cada área de riego; con la finalidad de alcanzar la optimización de sus recursos y con el propósito de conocer objetivamente su realidad, y considerar las medidas a tomar para corregir ineficiencias en las áreas de riego que la presenten.
Este artículo tiene como propósito profundizar en las bases conceptuales y alcance de las técnicas DEA, cuya aplicación en los últimos años se ha extendido al sector agrícola para conocer la eficiencia relativa de cada zona irrigada, y que sería muy factible aplicarla en el país para saber cuál sería la situación óptima de cada zona de riego con el propósito de mejorar la gestión del agua de riego y elevar su productividad para obtener mayores ingresos económicos.
Fundamentos del análisis envolvente de datos
El Análisis de Envolvente de Datos es una metodología basada en modelos de programación lineal, propuesta por primera vez en 1978 por Charnes, Cooper y Rhodes, para estudiar la eficiencia relativa de un conjunto de unidades productivas, utilizando un procedimiento no paramétrico (Charles et al. 1978). Los autores desarrollaron dicha técnica veinte años después a partir de las investigaciones de Farrel (1957), quién proporciona una medida satisfactoria de eficiencia productiva que tiene en cuenta todos los Inputs (recursos empleados) y muestra como puede ser calculada.
El DEA comenzó con la tesis de Edwardo Rhodes, en la Carnegie Mellon University en Pittsburgh, dirigida por W. W. Cooper. Rhodes trabajaba en la evaluación de programas educacionales para estudiantes desaventajados que se aplicaban en escuelas públicas de los Estados Unidos y eran subvencionadas por el Gobierno Federal. El problema consistía en evaluar la eficiencia relativa de una serie de escuelas, considerando para la misma, que llevaba aparejado el manejo de múltiples parámetros de entrada y salida, sin emplear las técnicas tradicionales utilizadas hasta la fecha, fundamentadas esencialmente en modelos económicos de estudios en los precios (Aparicio 2007). La respuesta a este problema representó la primera formulación matemática del DEA, en su variante CCR según las iniciales de sus autores (Charnes, Cooper y Rhodes).
El DEA surge como una técnica para evaluar la eficiencia de una serie de elementos, denominados usualmente unidades de toma de decisión (DMU, pssi), empleándose para dicha evaluaciones múltiples entradas y salidas para cada una de las DMU consideradas. Las mismas deben ser comparables: tanto sus entradas como sus salidas deben ser medibles en unidades homogéneas para todas ellas. Dicho término permite referirse a un grupo amplio de unidades organizacionales que pueden ser personas, regionales de una organización, empresas, entes territoriales e incluso países.
Según Cooper et al. (2004), DEA ha abierto la posibilidad de que se emplee en los casos que han sido resistentes a otros métodos, debido a la compleja naturaleza (a menudo desconocida) de las relaciones entre las múltiples entradas y salidas que participan en muchas de estas actividades, las técnicas DEA presentan la ventaja de que no requieren asumir una forma determinada de función de producción, como ocurre en el caso de las fronteras estocásticas además de permitir un estudio con varios outputs, pero en cambio presenta algunas limitaciones, especialmente se puede citar que no contempla el error aleatorio de los datos, que en el caso de la agricultura puede llegar a ser significativo (Rodríguez 2003).
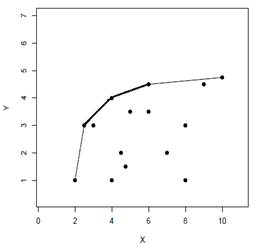
El Análisis Envolvente de Datos ha supuesto un enfoque alternativo a los planteamientos paramétricos clásicos del análisis de fronteras de producción. A diferencia de estos, cuyo objetivo es el ajuste a unos datos mediante herramientas estadísticas de una forma funcional previamente especificada, con las técnicas DEA se optimiza para cada DMU un modelo de programación matemática con el propósito de estimar una frontera lineal a trozos, determinada por las DMU eficientes en el sentido de Pareto; es decir, aquéllas no dominadas (Aparicio 2007) (ver la figura 1, donde las DMU vienen representadas por puntos en el plano en el caso de un input [X] y un output [Y]).
Según Aparicio (2007), en DEA no se requiere de ninguna hipótesis sobre la forma funcional, ni tampoco sobre la distribución de los errores. Simplemente se calcula una medida de eficiencia relativa a una frontera “extrema”, lineal, construida a partir de las observaciones muestrales, con la única condición de que todas las DMU queden envueltas por arriba por dicha frontera (figura 1), conocida a veces como frontera de mejores prácticas. La idea es detectar que unidades de la muestra están situadas sobre esa frontera de mejores prácticas. Detectar que unidades lo están haciendo mejor. Mejor en el sentido de consumir pocas (X) y producir muchas (Y). Por otro lado, una de las particularidades de las técnicas DEA sobre cualquier otra relación de eficiencia, radica en que los pesos asignados vienen determinados por la resolución del modelo.
En el caso del riego, con el uso de las técnicas DEA se puede evaluar el grado de pericia con que una unidad de riego (zona regable) lleva a cabo el proceso técnico de conversión de los inputs en outputs, comparando para ello su actividad con la de otras unidades de la muestra que, siendo tecnológicamente homogéneas, son eficientes relativamente. En resumen, el método DEA determinaría como eficientes a aquellas unidades de riego que, en términos relativos, consuman menos inputs (agua, mano de obra, insumos, energía) para un nivel de output (valor de la producción) dado; lo que puede ayudar a los gestores de la gestión del agua a conocer donde su aplicación va a generar un beneficio mayor.
Formulación de los modelos DEA
Para entender cómo funcionan los modelos DEA se necesita introducir algunos conceptos básicos de la teoría económica de la producción. En este sentido, se define la productividad de una determinada DMU como la relación existente entre el producto que se obtiene y los recursos empleados en su producción (y/x), para el caso de una sola salida y una sola entrada. Es una forma de medir cómo se están aprovechando dichos recursos, en el caso de que en una DMU existan varias entradas y varias salidas la expresión matemática que se propone es la siguiente. (ecuación 1):
Donde:
j |
1, 2,…, n subíndice para las DMU |
i |
1, 2,…, m subíndice para las entradas |
k |
1, 2,…, s subíndice para las salidas |
x ij |
cantidad de entrada o recurso i utilizado por una DMU j. |
y kj |
cantidad de salida o resultado k que produce una DMU j. |
u ij y v kj |
son los pesos correspondientes a cada entrada y salida, que hace adimensional las expresiones de entrada y salida virtual. |
m |
número total de entradas consideradas. |
s |
número de salidas de la DMU. |
Sin embargo, las técnicas DEA utilizan un nuevo concepto que se conoce como eficiencia relativa, para comparar una unidad con respecto a otra similar debido a que existen muchas variables importantes a ser tenidas en cuenta. Dicha eficiencia se determina de la siguiente manera. (ecuación 2):
Una aplicación práctica de la metodología DEA
Con un propósito exclusivamente didáctico y explicativo de la metodología DEA para evaluar la eficiencia en una organización. En la tabla 1 se recogen los datos ficticios de 8 empresas agropecuarias, cada una de ellas posee una variable de entrada (superficie regada) y una variable de salida (valor de la producción agrícola). Se desea conocer, cuál de esas empresas está haciendo mejor las cosas en el sentido de: consume pocos recursos y produce mucho. Este es uno de los objetivos de las técnicas DEA y del análisis de eficiencia, saber quién está haciendo mejor las cosas.
Tabla 1 Datos para ejemplificar las técnicas DEA.
| Empresas | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Superficie regada (ha) | 2 | 3 | 4 | 3 | 5 | 5 | 6 | 8 |
| Valor de la producción agrícola (millones de pesos) | 10 | 20 | 30 | 30 | 40 | 20 | 30 | 50 |
| Relación (valor de la producción agrícola/superficie regada) | 5,0 | 6,67 | 7,5 | 10,0 | 8,0 | 4,0 | 5,0 | 6,25 |
| Scores de eficiencia | 0,50 | 0,67 | 0,75 | 1,00 | 0,80 | 0,40 | 0,50 | 0,63 |
Para saber cuál de las empresas lo está haciendo mejor, se aplicó el criterio del ratio (y/x o relación del valor de la producción agrícola/superficie regada), que permitirá conocer cuánto miles de peso se consigue por superficie regada. Analizando los valores de la tabla 1, se puede observar que la empresa que tiene mejores resultados es la D, ya que consigue 10 mil pesos por hectárea regada. Por lo tanto, se puede decir que dicha empresa es la más eficiente de todas en cuanto al uso de recursos y la obtención de resultados.
En la última fila, se muestra los valores de eficiencia mediante la normalización de la fila anterior. Esta normalización consiste, en dividir el ratio entre su máximo valor que para este ejemplo es 10, lo cual permitirá obtener valores entre 0 y 1. Siendo 1 lo mejor que se puede encontrar y 0 lo peor. Estos valores son conocidos también como scores de eficiencia. Estas puntuaciones de eficiencia al estar entre 0 y 1, permite interpretar cualquier resultado, en cualquier base de datos, en cualquier contexto, cerca del 1 significa lo mejor que puede pasar y cerca de 0 lo peor.
Si se analiza ahora gráficamente el ejemplo, en la figura 2 se representa los puntos de las 8 empresas estudiadas. Los ratios que se han calculado coinciden con la pendiente de la recta que pasa por el origen y por el punto determinado que uno quiera; por ejemplo, la pendiente de la recta que pasa por 0 y por F tiene un valor de 4. Los valores de los ratios que se han calculado tienen una interpretación geométrica en términos de pendientes de rectas que pasan por el origen de coordenadas. Por lo que, analizando el gráfico solamente hay una empresa eficiente, la D, que es la que tiene mayor pendiente (10) y su recta envuelve los datos por arriba como si fuera un paraguas. Siendo esa la frontera de mejores prácticas hacia la cual tienen que tender las demás empresas para llegar a ser eficientes.

Fig. 2 Representación gráfica de la superficie regada y la producción agrícola en diferentes empresas.
Partiendo de este concepto de Ratio en 1978, Charnes, Cooper y Rhodes generalizaron dicho concepto para medir eficiencia cuando tienen varios output e input introduciendo el concepto de peso. Peso de cada variable, peso de cada dimensión. Se pasa del concepto de dos dimensiones como vimos en el ejemplo a una función donde se evalúa la sumatoria de todos los output entre la sumatoria de todos los input.
Este concepto ya se conocía en la literatura, pero lo que se conocía es, que los pesos eran fijados por unos expertos. Pero esto no era lo que querían hacer los autores. Dichos investigadores jugaron con este concepto de eficiencia asociado al ratio pero en el cual los pesos quedaran libres y que fueran los propios datos que nos indicaran cuánto valen los pesos.
Modelo básico de Charnes, Cooper y Rhodes (CCR).
El modelo consiste en la resolución de n problemas de maximización, correspondientes a cada una de las unidades cuya eficiencia se quiere evaluar. La función objetivo elige los pesos que hacen máxima la eficiencia hJ de la DMU que se estudia. La expresión matemática que maximiza la eficiencia, con la libertad de elegir los pesos se expresa de la siguiente forma. (ecuación 3):
Sujeto a:
Donde: h J : eficiencia de la DMU que se estudia; Ɛ: es un número real estrictamente positivo. Este valor representa una constante no-arquimediana (menor que cualquier número real positivo), y por tanto, en las restricciones donde aparece, se les obliga a los pesos a que nunca puedan ser nulos.
Este modelo de optimización lo que recoge es que, para cada DMU, para cada empresa; determinar unos pesos que maximicen el rendimiento de dicha empresa. Que la coloquen en la mejor posición posible. Al final lo que se obtiene es unos pesos, un valor óptimo de esa función objetivo. Es decir, un score de eficiencia entre 0 y 1.
Este modelo DEA creado por los autores se conoce como CCR y, puede construirse con dos objetivos diferentes: maximizar las salidas, manteniendo la cantidad de entradas (modelo orientado a salidas) o minimizar las entradas, manteniendo los niveles de salidas (modelo orientado a entradas). Esta metodología busca establecer qué empresas de una muestra determinan la superficie envolvente o frontera de producción eficiente. La distancia radial de una empresa hacia la frontera provee la medida de su eficiencia. Para resolver el modelo lineal fraccional (ecuación 3), los autores llevaron a cabo un proceso de transformación de variables y obtuvieron un modelo lineal equivalente. La forma envolvente de ese modelo CCR, orientado a entradas, para DMUj, se muestra a continuación. (ecuación 4):
Sujeto a:
Donde: λ
j
y θ
J
son variables del modelo;  y
y  variables de holgura de input y output, respectivamente y x
ij
y y
kj
son las entradas y salidas de la DMUj, respectivamente. En este caso, se evalúa la eficiencia de la DMU o (DMUj = DMUo).
variables de holgura de input y output, respectivamente y x
ij
y y
kj
son las entradas y salidas de la DMUj, respectivamente. En este caso, se evalúa la eficiencia de la DMU o (DMUj = DMUo).
Resolviendo este modelo de programació n J veces, una para cada DMU, se obtiene un vector de estimaciones de eficiencia técnica. Una unidad es 100% eficiente si y solo si θ* = 1 y

 para todo i y r. Una puntuación igual a 1, junto con valores nulos para las holguras, indica que la unidad en cuestión obtiene una producción dada a partir del consumo mínimo de los recursos disponibles para ella y las condiciones bajo las que opera.
para todo i y r. Una puntuación igual a 1, junto con valores nulos para las holguras, indica que la unidad en cuestión obtiene una producción dada a partir del consumo mínimo de los recursos disponibles para ella y las condiciones bajo las que opera.
Una puntuación que es menor que 1 (θ*< 1) indica que la unidad productiva evaluada es técnicamente ineficiente, por cuanto puede reducir las cantidades empleadas de todos sus inputs en una proporción igual a (1 - θ*).
El modelo CCR asume que todas las DMU operan a escala óptima, asumiendo rendimientos constantes a escala (CRS, pssi). No obstante, rara vez el mercado funciona de forma ideal, siempre existe limitaciones financieras, mercados de competencia imperfecta, etc. que hacen que el aumentar la cantidad de inputs no produzca el mismo aumento en la cantidad de outputs obtenida. La agricultura es un claro ejemplo de lo anteriormente expuesto, no por aumentar la cantidad de agua suministrada a los cultivos vamos a obtener un aumento linealmente proporcional en el volumen de cosecha obtenida.
Para intentar contabilizar este efecto en la obtención de la eficiencia, en 1984 se presentó el modelo DEA para retornos variables a escala, desarrollado por Banker, Charnes y Cooper (BCC), este modelo permitirá calcular la eficiencia técnica pura (ETP), esto es, la eficiencia separándola de los efectos de escala (Banker et al. 1984).
Modelo de Banker, Charnes y Cooper (BCC).
El modelo BCC va a presentar una frontera curva, va a tomar más puntos como eficientes y por tanto, va a ser más útil para determinar eficiencias locales, en ámbitos de aplicación en los que imperan una serie de restricciones que impiden ciertos valores de producción, pero que aún así, hace que una DMU, dentro de ese marco, esté trabajando de manera eficiente (Rodríguez 2003).
Para que el modelo considere los retornos de escala variables habrá que introducir, a partir del modelo RATIO linealizado, alguna restricción o alguna variable que le indique al modelo que cada DMUJ tiene que ser comparada con aquéllas de su tamaño y no con todas las unidades presentes en el problema. Modificando la forma envolvente del modelo CCR orientado a entradas se obtiene la formulación del modelo BCC orientado a entrada. (ecuación 5):
Sujeto a:
Se puede observar que la restricción adicional que aparece en el dual de este modelo [suma de las componentes del vector (λ 1, λ 2 ,…,λ n ) igual a uno] obliga a que la proyección de la unidad se efectúe sobre el hiperplano que forman las unidades más productivas de su tamaño. En general, para este caso, aparecerán unidades que no eran eficientes en el anterior modelo (retornos de escala constantes) y que sin embargo en este modelo sí lo son. De ahí que la frontera eficiente esté formada, en general, por más unidades que en el modelo CCR.
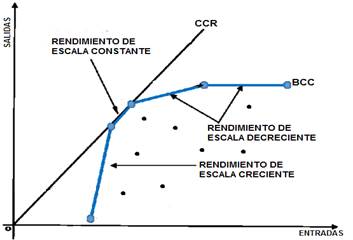
La diferencia que existe entre el modelo CCR y el BCC se debe a que, la frontera del CCR emplea un único punto, por lo que sólo una DMU es eficiente, mientras que el modelo BCC ofrece más soluciones eficientes, que van a definir la curva de producción óptima, adaptándose mejor a las condiciones reales del mercado, por tanto, se puede afirmar que el modelo de retornos variables va a envolver más datos y de aquí se deduce que la eficiencia técnica pura siempre va a ser menor o igual que la eficiencia técnica global (figura 3).
Datos entradas/salidas y rendimientos de escala
Al aplicar DEA para la evaluación comparativa del rendimiento del riego, se debe tener cierto grado de precaución en el número y la selección de variables que se analizarán y procesarán. La selección de variables debe estar estrechamente relacionada con los objetivos del estudio y el proceso productivo que se evalúa. Además, existe el riesgo de que la adopción de demasiados indicadores de desempeño permitiría a la técnica DEA considerar eficientes todas o la mayoría de las asociaciones de usuarios analizadas y, por lo tanto, no proporcionaría ninguna información sobre las desviaciones de la situación actual con respecto a la gestión óptima (Alcón et al. 2017).
Evaluar en la agricultura todas las entradas (inputs) y las diversas salidas (outputs) que se utilizan y que se van a obtener durante la campaña agrícola sería algo imposible. Al evaluar el uso eficiente del agua de riego mediantes técnicas DEA, el agua, no puede ser considera como algo aislado, sino como un integrante de un proceso de producción en el que van a intervenir varios elementos.
Autores como Rodríguez (2003) y Olmedo (2017), en un estudio de eficiencia mediante técnicas DEA en las áreas de riego de Andalucía (España) y Sonora (México) emplearon como variables de entradas tres factores que están presentes en el proceso de producción agrícola que son: 1) superficie regada (ha), 2) volumen de agua total para la superficie regada (millones m³) y 3) la mano de obra empleada (UTA, unidad de trabajo anual) ó los costos de producción (millones de pesos); y como variable de salida (output) el valor total de la producción agrícola (millones de pesos) (figura 3). Esto permitió caracterizar la producción de una forma muy aproximada, permitiendo distinguir entre los diversos tipos de agricultura, al considerar las entradas que más van a diferir entre unos sistemas y otros.
Por otro lado, la metodología DEA presenta dos tipos de tecnologías: (1) Retornos de Escala Constante (CRS, pssi) y (2) Retornos de Escala Variables (VRS, pssi). La tecnología CRS considera como unidad más eficiente la que proporcione más salidas, consumiendo menos recursos (eficiencia global), mientras que en la tecnología VRS, existirá una frontera de eficiencia representada por las unidades que son eficientes técnicamente y todos los puntos que forman una combinación lineal convexa. Las unidades con eficiencia técnica son eficientes en comparación con las de su tamaño. Según Rodríguez et al. (2008), la escala de la actividad (es decir, el tamaño de la organización) tiene un efecto importante en su eficiencia.
Los rendimientos de escala constante, significa que, si los recursos utilizados aumentan en determinada proporción, el rendimiento obtenido aumenta exactamente en la misma proporción. En el caso de los rendimientos de escala variables, significan que se tienen rendimientos (outputs) crecientes y/o decrecientes; donde en el primer caso el rendimiento se incrementa en mayor proporción que los recursos (inputs) utilizados y en el segundo caso, el incremento en rendimiento es menor, que el incremento porcentual de los recursos (Olmedo 2017).
Cuando una unidad domina a otra es porque tiene menos entradas y/o más salidas la tecnología considerada. Si por el contrario la DMU no es eficiente, el modelo la proyecta sobre la frontera eficiente y mide la eficiencia de la DMU en términos de reducción del consumo de las entradas e incremento en la producción de salida. Hay diferentes maneras de realizar la proyección y medición de la distancia entre la DMU y el punto sobre el que se proyecta. La proyección puede hacerse de la entrada (orientación a la entrada) o de la salida (orientación a la salida). Así, la orientación de entrada consiste en la reducción tanto como sea posible de todos los recursos de forma equi-proporcional sin reducir las salidas. Por otra parte, la orientación de salida consiste en incrementar tanto como sea posible los productos de forma equi-proporcional sin un incremento de las entradas (Cooper et al. 2004). El modelo orientado a entrada (I-O) mide la capacidad de una DMU para mantener la misma capacidad de producción utilizando un mínimo de insumos. El modelo orientado a salida (O-O) se refiere a la capacidad de una DMU para lograr el volumen máximo de producción con los insumos disponibles.
Conclusiones
Las técnicas de Análisis de Envolventes de Datos son válidas para evaluar la gestión de procesos en el sistema de la agricultura, en particular la relación recursos-resultados en las actividades relacionadas con el riego agrícola.
La aplicación de estas técnicas permite diferenciar las áreas que obtienen una mejor relación recursos-resultados de aquellas que obtienen niveles por debajo de sus posibilidades y constituyen una herramienta útil para identificar las prácticas de riego más adecuadas en escenarios agrícolas.
La utilización adecuada de estas herramientas aporta información útil para el diseño de políticas gubernamentales que promuevan mayores niveles de eficiencia en la agricultura cubana.
Las técnicas DEA contribuyen a disminuir el consumo de agua, especialmente crítico en el regadío cubano, detectar ineficiencias locales, comparar áreas de riego de muy diversa índole, además de detectar qué zonas presentan un mayor potencial de crecimiento.