INTRODUCCIÓN
Una vez recogida la información acerca de las variables de estudio se procede a su procesamiento y posterior presentación a través de las tablas (o cuadros estadísticos) y de los gráficos, aunque ciertos resultados pueden ser presentados en forma de texto.
Específicamente en el caso de las tablas, su cuerpo esta constituido por filas y columnas que expresan la o las variables a presentar y, generalmente, la distribución de frecuencias (absolutas y relativas) de sus correspondientes categorías; frecuencias que se distribuyen en las celdas configuradas a partir del entrecruzamiento de las filas y columnas antes mencionadas.
Las tablas estadísticas o de resultados pueden ser unidimensionales cuando en ellas se representa una sola variable (las llamadas “tablas de frecuencias”) o bidimencionales cuando se representan dos variables (conocidas como “tablas de relación de variables”). También pueden ser multidimensionales, en las que están representadas tres o más variables, pero son raras en los informes de investigación por su gran tamaño, excesiva información y difícil lectura e interpretación.
Aunque se reconoce en la literatura especializada la existencia de diversos tipos de errores en la elaboración de las tablas,1) en esta oportunidad nos vamos a referir a dos situaciones que, con una muy elevada frecuencia, suelen ser observadas en los trabajos de terminación de la especialidad.
DESARROLLO
La primera de las situaciones a analizar tiene su origen en el intento del investigador-residente de evitar los cuestionamientos a la simplicidad de su investigación; simpleza derivada de la presentación de sus resultados a través, predominantemente, de tablas de frecuencias o unidimensionales. Para evadir dicha simplicidad en la presentación de los resultados, se procede entonces a la utilización de tablas de relación de variables (bidimencionales), lo cual, en una primera mirada, no aparenta ser una decisión incorrecta.
El problema se presenta a partir del establecimiento de relaciones entre variables “sin ton ni son”; o sea, el establecimiento de relaciones entre variables con el único propósito de … “cruzar” variables. En este sentido, se observa el uso indiscriminado de variables como la edad y el sexo; variables con las cuales se suelen relacionar el resto (o la mayoría) de las variables de la investigación.
En algunas ocasiones se llega al extremo del entrecruzamiento anárquico de las variables investigadas. La resultante de esta manera de presentar los resultados es la inclusión de un gran número de tablas en el informe final que hacen excesivamente extenso el documento; tablas (resultados) cuya interpretación se hace difícil y que apenas aportan a la solución de la interrogante inicial y, por ende, al cumplimiento del objetivo investigativo.
Para la solución de este problema es capital que el investigador comprenda que toda relación entre variables que se presente en los resultados debe ser consecuencia de un juicio previo que le otorgue un mínimo de plausabilidad a la relación que se pretende establecer. Este juicio, que puede llegar incluso a la condición de hipótesis, debe estar sustentado en el cuerpo de conocimientos existente acerca del objeto de estudio, o ser el resultado de la observación reflexiva y creativa de la práctica cotidiana del que investiga.
Expresado de otra manera, está justificado el entrecruzamiento de variables cuando se espera determinado comportamiento de las categorías de una variable en dependencia del comportamiento de las categorías de la otra variable con la cual se está relacionando la primera. La idea anterior constituye el criterio determinante para la presentación de resultados a través de tablas bidimencionales o de relación de variables.
A manera de ejemplo, este postulado se cumple en un estudio sobre pacientes con enfermedad pulmonar obstructiva crónica (EPOC) descompensada, en el que se pretende explorar la existencia de una posible relación (solo a un nivel descriptivo, no analítico) entre el estado de gravedad al momento de la admisión hospitalaria y el estado al egreso. Un rápido análisis de esta investigación ejemplo permite identificar que es plausible la posibilidad de una relación entre el estado de gravedad al ingreso y el estado final del paciente; con ello se cumple el criterio necesario que justifica el entrecruzamiento de ambas variables y, a partir de ello, la presentación de los resultados a través de una tabla de relación de variables.
La situación hasta aquí descrita está vinculada con la segunda situación a analizar.
Observemos ahora las siguientes tres variantes de una tabla en las que se presentan los resultados del estudio-ejemplo anterior.
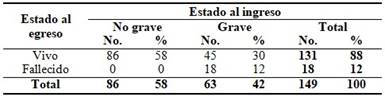
Variante A:
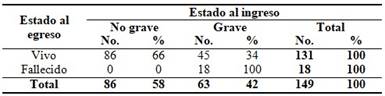
Variante B:
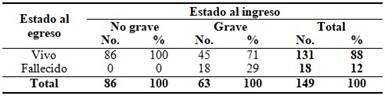
Variante C:
Resulta evidente que los valores que ocupan las celdas correspondientes a las frecuencias absolutas (columnas del número de casos) son los mismos en las tres variantes de la tabla. En cambio, las variantes poseen diferencias en los valores de las celdas correspondientes a las frecuencias relativas (columnas de porcentajes). En resumen, todas las variantes muestran los mismos resultados en términos absolutos pero difieren entre sí en los resultados relativos, debido a que los porcentajes han sido calculados, indistintamente en cada variante, en base al total de los pacientes, por las columnas y por las filas. Entonces, ¿cuál de estas variantes es la correcta?
Para responder esta pregunta debemos aclarar que no es suficiente el cumplimiento del criterio determinante para la presentación de resultados a través de tablas de relación de variables antes expuesto para que los resultados de la investigación estén adecuadamente representados en una tabla estadística. Y es que toda relación tiene implícitamente un sentido de dirección; en otras palabras, existe un sentido de dependencia en la relación entre las variables implicadas.
Para ilustrar esta idea regresaremos a la investigación tomada como ejemplo, sobre la posible relación entre el estado de gravedad de pacientes con EPOC descompensada al momento del ingreso hospitalario y el estado del paciente al egreso. El análisis de este objeto permite identificar la condición determinante de la variable “estado al ingreso” (grave o no grave) sobre la variable “estado al egreso (vivo o fallecido); o sea, es razonable suponer que la primera determina a la segunda, o lo que es lo mismo, que el estado al egreso será dependiente del estado al ingreso. No a la inversa. Este análisis es fundamental para la decisión relativa a la manera de calcular las frecuencias relativas o porcentajes a presentar en la tabla.
La importancia de la claridad en el sentido de dirección de la relación que se investiga está asociada a otro de los fenómenos frecuentemente constatado en las tablas estadísticas de los trabajos de terminación de la especialidad: el cálculo de las frecuencias relativas sin tener en cuenta la condición de independencia y dependencia de las variables estudiadas; o sea, sin respetar el sentido de dirección en la relación que se investiga.
Desde este punto de vista, en nuestra investigación ejemplo, la forma más apropiada de presentar los resultados se corresponde con la variante C de la tabla; variante que nos muestra que el 29 % de los pacientes que ingresaron en estado de gravedad tuvieron un desenlace fatal, a diferencia de los pacientes que no ingresaron graves, entre quienes no hubo fallecimientos.
¿Significa esto que las otras tablas están incorrectamente elaboradas? En realidad no, solo que requieren lecturas un poco diferentes. La representación de los resultados en la variante C es la resultante de un análisis “hacia delante” de los datos obtenidos: se parte del estado del paciente al ingreso para llegar al estado al egreso; por esta razón el porcentaje ha sido calculado por las columnas, al representar estas a la variable “estado al ingreso”.
En cambio, la variante B resulta de un análisis “hacia atrás” de los datos, pues se parte del estado al egreso para arribar al estado al ingreso; entonces, el porcentaje ha sido calculado por las filas. Los resultados de esta tabla expresan que la totalidad de los pacientes fallecidos estaban graves al momento del ingreso, a diferencia de los pacientes que fueron egresados vivos en quienes solo el 34 % tenía gravedad al ingresar.
En la variante B se expone la distribución de frecuencias de la variable “estado de gravedad al ingreso” según la variable “estado al egreso”. En la variante C, se precisa la distribución de frecuencias de la variable “estado al egreso” según la variable “estado de gravedad al ingreso”.
Como se puede observar, y aunque se sugiere la variante C para este ejemplo en particular, queda claro que la decisión de cómo calcular las frecuencias relativas (específicamente los porcentajes) está determinada por el punto de partida (o de entrada) y el punto de llegada (o de salida) que se asuma en el análisis del fenómeno que se investiga.
En otras ocasiones solo se desea determinar la correspondencia o coincidencia entre las categorías de dos variables, sin que necesariamente exista una relación (al menos evidente o definida) de dependencia entre estas, como es el caso del típico entrecruzamiento entre la edad y el sexo. En este caso, la distribución de las frecuencias relativas como aparecen representadas en la variante A es totalmente permisible.
CONCLUSIONES
La confección de las tablas para la presentación de los resultados de la investigación constituye un área del informe final en la cual, en no pocas ocasiones, se ponen de manifiesto deficiencias del trabajo de terminación de la especialidad. La importancia de este asunto radica en que los errores en la presentación de los resultados obtenidos tienen una incidencia directa en el subsiguiente proceso de interpretación de esos resultados y, consecuentemente, en la elaboración de las conclusiones y las recomendaciones.
Por tanto, la utilización adecuada y no esquemática del entrecruzamiento de variables en los estudios descriptivos, y la selección de la manera más apropiada para el cálculo de las frecuencia relativas o porcentajes constituyen aspectos a no descuidar por el residente en la ejecución de la investigación y en la redacción de su informe final.