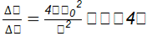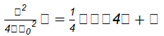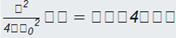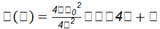Servicios personalizados
texto en 
Inglés (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Uno de los principales problemas que enfrenta el mundo de hoy es el cambio climático, el cual incide en todos los procesos socioeconómicos de la sociedad. En múltiples foros internacionales, la comunidad internacional se ha pronunciado al respecto para lograr acciones concretas a favor del cuidado y protección del medio ambiente.
Para Cuba, que también vive momentos difíciles para su desarrollo socioeconómico, resulta de vital importancia el desarrollo sostenible, por ello se han promovido en la Agenda 2030 los objetivos para el logro de este propósito.
La Educación Superior en Cuba dedica numerosos recursos materiales, financieros y humanos a la formación consciente y participativa del futuro egresado, en función de lograr su implicación en la construcción de un futuro sostenible. Ministerio de Educación Superior, (MES, 2017)
En esta dirección se coincide con (Fuentes, 2008), en que el proceso de formación de los profesionales se cumple cuando se desarrollan las capacidades cognoscitivas, las capacidades espirituales y las capacidades creativas que les permiten sensibilizarse con la realidad del entorno, y convertirse en agentes de transformación social.
En el ingeniero agrónomo, lo antes expuesto tiene incidencia debido a que es considerado el profesional más integral entre los encargados de la producción agropecuaria, requiere del conocimiento y aplicación de métodos científicos y de la tecnología con el fin de manejar los recursos naturales de forma racional y alcanzar el máximo rendimiento de las especies cultivadas o de animales, obteniendo producciones con calidad al menor costo posible (MES, 2017).
La disciplina Matemática es parte del currículo de la carrera de Agronomía, la cual tiene como objetivo el tratamiento de la información matemática y la toma de decisiones para la solución a problemas agronómicos, empleando métodos y procedimiento matemáticos y de cómputo, así como modelos que permitan la toma de decisiones en problemas relacionados con la agronomía. (MES, 2017)
De manera que cobra una especial importancia el tratamiento de los contenidos matemático en los estudiantes de la carrera de Agronomía, a partir de un proceso de comprensión y obtención de nuevos conocimientos, lo cual implica ocuparse de que los estudiantes no solo aprendan elementos concretos del contenido matemático, sino también, las conexiones que se establecen entre ellos en un contexto profesional, de modo que puedan explicar el contenido con sus palabras y usarlo en la solución a problemas profesionales.
En este sentido se puede afirmar que la resolución de problemas es uno de los métodos más utilizados para lograr un aprendizaje activo y creador; investigadores como (Rizo y Campistrous, 1999), hacen referencia al proceder generalizador para la resolución de problemas, los cuales constituyen vías para la apropiación de habilidades, valores y conocimientos, preparándolos para que puedan detectar problemas, revelar conflictos, buscar soluciones y aplicarlas con independencia cognoscitiva.
Por su parte, (Chérrez, 2023) dirige su investigación a la resolución de problemas matemáticos en la Educación Superior, ponderando que es este el camino para lograr la apropiación de conocimientos y el desarrollo de habilidades a partir de la contextualización e interpretación lógica de los contenidos matemáticos y su aplicación en la solución de problemas concretos de la vida y de su futura profesión.
A pesar de lo valioso de estas aportaciones, se considera que debe profundizarse en las particularidades que distinguen la dinámica del profesional de la carrera de Agronomía a través de una lógica coherente que posibilite alcanzar niveles superiores en la sistematización de la funcionalidad del contenido matemático y su generalización contextualizada en las exigencias medioambientales del entorno de actuación.
Lo anterior genera que en el proceso de enseñanza-aprendizaje de la Matemática se aprecien carencias en la aplicación de estrategias heurísticas, métodos y procedimientos matemáticos necesarios para resolver problemas relacionados con la profesión, bajos resultados académicos en la asignatura y deficiente calidad de las calificaciones obtenidas por los estudiantes, así como insuficiente interés por el estudio de la Matemática, al no percibir su aplicabilidad en la solución a problemas profesionales.
De acuerdo con lo planteado, se declara como problema a resolver, ¿cómo contribuir a la formación del estudiante de la carrera de Agronomía, para enfrentar la solución a problemas matemático-profesionales?
Desarrollo
Para el desarrollo de este trabajo se seleccionó una muestra de 25 estudiantes de primer año de la carrera de Agronomía, de una población de 54.
Se realizó el estudio y análisis de los documentos normativos de la carrera como el Plan de Estudio, la Planificación estratégica del país relacionada con la producción de alimentos vinculada al territorio y el diagnóstico del aprendizaje de los estudiantes hacia la resolución de problemas.
La resolución de problemas en la enseñanza de la matemática posibilita la adquisición de conocimientos con un mayor nivel de solidez, de profundidad, de posibilidad de transferirlo y de generalizarlo de manera flexible e independiente (Suarez y Meléndez, 2023), siendo lo anterior, sin duda, la llave para lograr un aprendizaje integral en los estudiantes, de modo que permita al futuro egresado potenciar la percepción de riesgo en el ejercicio de su profesión y en la interacción con la sociedad.
Luego, los métodos problémicos propician que los estudiantes, guiados por el profesor, se introduzcan en el proceso de búsqueda de la solución a problemas nuevos para ellos, gracias a lo cual, aprenden a adquirir los conocimientos de forma independiente, a emplear los antes asimilados, y a dominar la experiencia de la actividad creadora.
Los procedimientos de solución en la enseñanza de las ciencias se pueden clasificar en dos grandes clases: los algorítmicos y los heurísticos, (Ballester et al., 2018). Este mismo autor se pronuncia acerca de los procedimientos heurísticos al identificarlos como acciones que apoyan la realización consciente de actividades mentales complejas y exigentes. Propician la asimilación de los conocimientos, su capacidad para resolver problemas para los cuales no conocen procedimientos algorítmicos, así como el desarrollo del pensamiento creador. Estos pueden dividirse en principios, reglas y estrategias, los cuales pueden ser generales y especiales.
En el tratamiento de los contenidos matemáticos en la carrera de Agronomía, el estudio de las situaciones típicas de la Matemática, así como en la solución de problemas son empleados:
Principios: analogía, modelización, principio de reducción, el modelado, generalización y consideración de casos especiales y casos límites.
Reglas heurísticas: que tienen carácter de impulsos en el proceso de análisis del problema y búsqueda de la vía de solución.
Reglas generales: separar lo dado de lo buscado, recordar conocimientos relacionados con lo dado y lo buscado y buscar relaciones entre ellos.
Estrategias heurísticas: las que constituyen los procedimientos principales para buscar los medios concretos que se necesitan para resolver un problema matemáticos profesional y para buscar la vía de solución, ellas son: el trabajo hacia adelante o combinación de estrategias.
Los autores de este trabajo consideran que debe profundizarse en las particularidades que distinguen la dinámica del profesional de la carrera de agronomía a través de una lógica coherente que posibilite alcanzar niveles superiores en la sistematización de la funcionalidad del contenido matemático y su generalización contextualizada, siendo esta una de las causas por las que continúan manifestándose dificultades con la resolución de problemas matemáticos profesionales en la carrera de Agronomía.
En este sentido, la asignatura matemática en el plan de estudio de la carrera de Agronomía encierra una perspectiva abstracta pero también práctica, por ello tiene definido como encargo: el tratamiento de la información matemática relacionada con las funciones del ingeniero agrónomo en los procesos agropecuarios y con la toma de decisiones para la solución de los problemas que se presentan en los mismos, empleando para ellos métodos matemáticos y de cómputo, así como modelos que permitan evaluar la factibilidad o tendencia de determinadas alternativas (MES, 2017).
Para lograr tal propósito se debe tener en cuenta que los problemas profesionales en la Ingeniería Agrónoma, se centran en la necesidad de generar alimentos y materias primas para la satisfacción de necesidades humanas e industriales demandadas por la sociedad, garantizando la conservación de los recursos naturales de los que dispone y la sostenibilidad de los sistemas de producción agropecuaria. (MES, 2017)
A pesar que se pondera el método problémico para dichos futuros profesionales, es aún insuficiente su visión desde la integración con una visión ecológica sostenible de los procesos formativos del futuro ingeniero agrónomo.
En este sentido, los problemas profesionales deben conectarse con el conocimiento matemático para transformar las necesidades sociales. Esta perspectiva logra despertar en los estudiantes el interés por lo desconocido, la apropiación del contenido convirtiéndolos en una necesidad y motivación constante, a partir de la valoración de informaciones profesionales, sustentada en la aplicación de procedimientos matemáticos, que según (Fonseca, 2023), deberán convertirse en una herramienta importante para su futura profesión.
La profesionalización del contenido es un camino para resolver esta limitación, por lo que resulta importante tener en cuenta lo expresado por Castillo (2001) al definirla como: el proceso en el que la formación inicial propicia la interrelación: teoría-práctica-comunicación-motivación del estudiante, interesándolo en su futuro desempeño profesional, a partir de la solución de tareas que se identifican con los problemas más comunes del ejercicio de su profesión y de su encargo social.
En el caso que se investiga, en los profesionales de la Agronomía, es importante la educación ambiental con tendencia hacia la agroecología, siendo esta la que reconoce los sistemas de producción como agroecosistemas y, por tanto, su manejo sostenible (MES, 2017); así como lograr una gestión eficiente en los procesos que se desarrollan en los sistemas de producción agropecuarios contribuyendo al desarrollo de una agricultura sostenible sobre bases agroecológicas, que integren la sostenibilidad agroenergética y la seguridad alimentaria.
Desde el modelo del profesional, se evidencia la necesidad de relacionar la Matemática con la profesión y la educación ambiental cuando se plantea: es necesario propiciar, desde las disciplinas de la carrera, el desarrollo de nuevos enfoques que involucren el manejo sostenible de los sistemas de producción agropecuaria, el empleo de tecnologías que se adecuen a las características locales y el respeto por el medio ambiente. (MES, 2017).
Un proceso importante dentro de la formación ambiental es el desarrollo de la sensibilidad ambiental, ella es garantía de la transformación de la realidad y de la sostenibilidad como meta profesional, lo cual resulta notorio para el estudiante de la carrera de Agronomía.
Al respecto (Rodríguez et al., 2023), enfatiza en la importancia de la construcción del conocimiento sobre las prácticas agrícolas con enfoque ecológico a partir de identificar las principales dificultades y limitaciones futuras relacionadas con la actividad productiva, económica y social en la comunidad, lo que fomenta el interés de los estudiantes por el aprendizaje, mejora su preparación y enriquece sus habilidades profesionales, faltándoles por explicar, con suficiente profundidad, una lógica coherente en la reconstrucción de dicho conocimiento desde el contenido matemático, que posibilite llevar consigo conocimientos, habilidades previas y estrategias de aprendizaje a las condiciones inherentes en nuevos contextos, desde una visión agroecológica.
Se trata, por tanto, de que el estudiante, en su formación, tenga que solucionar problemas profesionales en los que logre la aprehensión del contenido matemático relacionado con las situaciones que ocurren en los agroecosistemas de producción.
En este sentido, (Leyva y Machado, 2023), definen problematización matemática agroecológica como un proceso que expresa la contradicción entre lo conocido y desconocido, es además activo, dinámico de búsqueda, de indagación de vías de solución a situaciones problémicas planteadas por el profesor, que posibilita la construcción de conocimientos matemáticos en los estudiantes a partir de la interrelación de conocimientos y habilidades previas, los contenido profesionales y necesidades formativas en contextos agroecológicos, facilitando la comprensión funcional de dicho contenido.
Lo particular de la problematización matemática agroecológica es mostrar situaciones problémicas en las que se integren contenidos interdisciplinarios para lo cual se precisa de un algoritmo concreto para su solución e interrogantes que permitan arribar a conclusiones a través de la predicción y la toma de decisiones.
De acuerdo con lo anterior, el profesor debe plantear problemas matemáticos profesionales con varios niveles de complejidad y variabilidad en las que modelen situaciones y conflictos comunes y frecuentes de su futura profesión, que desde diferentes perspectivas didácticas logren, en los estudiantes, una mayor actividad cognoscitiva, para facilitar su motivación por el contenido matemático.
Para ello, se propone una estrategia didáctica, la cual se concibe como un sistema de acciones que permite, desde los contenidos de la Matemática, vincularse a los diferentes escenarios profesionales, con énfasis en la sostenibilidad agroecológica, dirigidos a la solución de problemas profesionales, que posibilitan gestionar eficientemente los procesos que se desarrollan en los sistemas de producción agropecuaria.
Para la elaboración de la estrategia propuesta se tuvo en cuenta el Plan de estudio E, el cual permitió articular los contenidos matemáticos y los profesionales-agroecológicos para lograr la transferencia matemática profesional.
La estrategia persigue como objetivo estructurar el tratamiento de los contenidos matemáticos en las carreras de Agronomía, para la solución a problemas matemático-profesionales; esta cuenta con tres momentos:
1er momento. Valoración del contenido matemático con orientación profesional-agroecológico.
2do momento. Sistematización del contenido matemático con orientación profesional-agroecológico.
3er momento. Evaluación del contenido matemático con orientación profesional-agroecológico.
Acciones de la estrategia.
Identificar en el Plan de Estudio, la relación interdisciplinaria entre los contenidos matemáticos y los de la especialidad (Matriz de articulación).
Orientar actividades de campo relacionadas con la búsqueda de información acerca de técnicas agroecológicas dirigidas a la sostenibilidad de los recursos naturales.
Realización de talleres para la elaboración de los problemas matemáticos profesionalizados a partir de la información suministrada por los estudiantes empleando procedimientos heurísticos y recursos audiovisuales.
Búsqueda y discusión de la vía de solución del problema matemático profesionalizado.
Interpretación del resultado dirigido a la toma de decisiones y la predicción teniendo en cuenta los riesgos y beneficios en los escenarios profesionales.
Ejemplificación.
Una vez identificada la relación interdisciplinaria se procedió a orientar las actividades extramatemáticas en los futuros escenarios profesionales, como organopónico, fincas y CPA, para que ellos investigarán las principales características y aplicación de técnicas agroecológicas. Los estudiantes investigaron sobre las técnicas de riego más utilizadas para contribuir al ahorro de agua y energía, entre las cuales se destaca el riego por aspersión localizado, con boquillas esféricas.
El problema que se presenta a continuación, con enfoque agroecológico, es fruto de un taller realizado con los estudiantes al culminar el tema de las ecuaciones diferenciales y sus aplicaciones y luego de haber sistematizado dicho contenido.
En una extensa área cultivada de maíz se aplica el riego por aspersión en el que se utilizan boquillas esféricas (figura 1) con gran número de agujeros iguales por los cuales sale el agua a la velocidad v 0 , describiendo un movimiento parabólico que cae sobre el suelo, para que sea aprovechada al máximo por las plantas. Se conoce que el alcance horizontal de riego se expresa a través de la ecuación diferencial
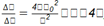; si inicialmente el chorro sale a una velocidad de 0,2m/s, con un ángulo de 15 0 se riega 0,5 m y por las condiciones del suelo se regula la boquilla con un ángulo de 22,5 𝑜 , ¿cuál será el alcance horizontal de riego?
Para la búsqueda de la vía de solución el profesor realiza preguntas de impulsos relacionadas con identificar el tipo de ecuación diferencial y su procedimiento de solución.
Por su parte los estudiantes son capaces de identificar la ecuación y la vía de solución.
Resolviendo la EDO de variable separable se obtiene:
Solución general de la ecuación diferencial
A partir de este momento el profesor, teniendo en cuenta las condiciones dadas en el problema, induce a los estudiantes a buscar el valor de los diferentes parámetros.
Los estudiantes logran identificar los parámetros y sustituirlos en la solución general.
Una vez calculados los parámetros los estudiantes proceden a calcular el alcance horizontal con un ángulo de 22,5 𝑜 .
Su gráfico se dilata con respecto al eje de las x hasta representar un radio de 0.901m
Respuesta. Al regular la boquilla con un ángulo de 22,5o, se logra una distancia de 0,501m
A partir del resultado obtenido se reflexionará con los estudiantes acerca de la decisión que se puede tomar regulando las boquillas, siendo este un método versátil y flexible que puede adaptarse teniendo en cuenta el tipo de cultivo y las condiciones del suelo; destacando que este uso sostenible del agua puede llegar ahorrar entre un 50% y un 70%, potenciando de esta manera una agricultura sostenible.
Conclusiones
Los estudiantes muestran un elevado interés y motivación por su especialidad, por investigar y profundizar sus conocimientos sobre cómo contribuir a lograr producciones agroecológicas-sostenibles de alimentos.
El trabajo permitió orientar metodológicamente a los docentes de la disciplina de Matemática sobre la contextualización agroecológica de los contenidos matemáticos.
La estrategia ofrece los conocimientos teórico-metodológicos a los docentes para integrar, de forma armónica, los contenidos matemáticos a problemáticas de la profesión y su empleo sistemático en los escenarios de la profesión con una perspectiva formativa agroecológica.
El aprovechamiento por parte de los profesores de las potencialidades del contenido de la asignatura y la tecnología moderna favorecen la solución a problemas profesionales dirigidos al manejo sostenible de los sistemas de producción agropecuaria.
