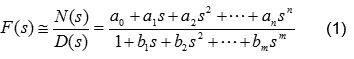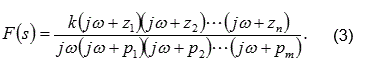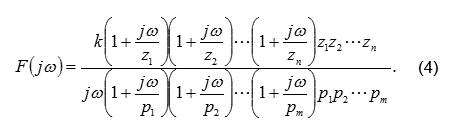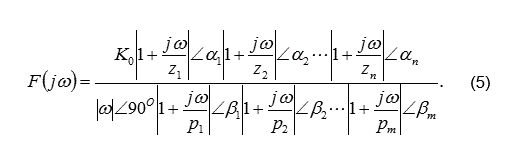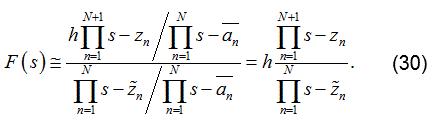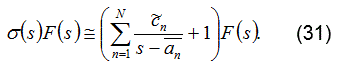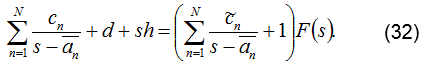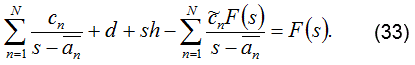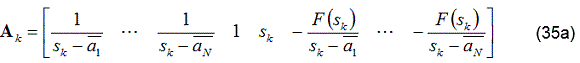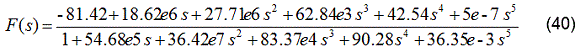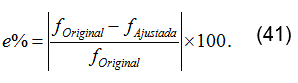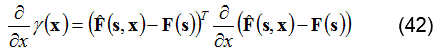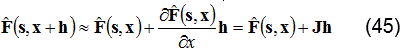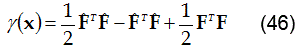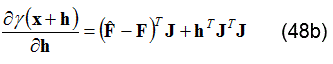TRABAJO TEORICOEXPERIMENTAL

 

Identificación de parámetros con métodos numéricos para el modelado de sistemas eléctricos con dependencia frecuencial

 

Identification of parameters with numerical methods for the modelling of electrical systems with frequency dependence

 

 

Msc. Eduardo Salvador Bañuelos Cabral, Dr. José Alberto Gutiérrez Robles, Dr. José Luis Naredo Villagrán , Msc. Julián Sotelo Castañón, Msc. Verónica Adriana Galván Sánchez, Msc. Jorge Luis García Sánchez

Centro de Investigación y Estudios Avanzados (Cinvestav), Guadalajara, México.

 

 

---

RESUMEN

El artículo presenta una descripción detallada de las técnicas más utilizadas para hacer ajuste racional de funciones del dominio de la frecuencia. Las técnicas son: Aproximación Asintótica de Bode, Mínimos Cuadrados Ordinarios, Mínimos Cuadrados Iterativamente Reponderados, Ajuste Vectorial y Levenberg-Marquardt. Estas técnicas se comparan aproximando una función analítica. Después, se aplican al ajuste racional de parámetros dependientes de la frecuencia de una línea de transmisión monofásica. El efecto del ajuste se evalúa considerando los casos de línea abierta, corto circuito y perfectamente acoplada. La transformada numérica de Laplace (NLT) se utiliza como referencia para la evaluación. Se concluye que la adecuada implementación de cada técnica depende de varios factores; del tipo de función a ajustar, del rango de ajuste, y otros. Además, no es posible garantizar que una de las técnicas siempre converja al mejor resultado. El artículo propone algunas guías para seleccionar la técnica más adecuada para una aplicación particular.

Palabras clave: Bode, Mínimos Cuadrados, Ajuste Vectorial, Levenberg-Marquardt, y Líneas de Transmisión.

---

ABSTRACT

This paper provides a detailed description of the rational fitting techniques that are most used to approximate frequency domain functions. The techniques are: Bode asymptotic approximations, Ordinary Least-Squares, Iteratively Reweighted Least-Squares, Vector Fitting and Levenberg-Marquardt. These techniques are compared by approximating of an analytic function. Then, the techniques are applied to the rational-fitting of the frequency-dependent parameters corresponding to a single-phase transmission line. The effect of the rational representations is evaluated considering transients on cases of open-ended, short-circuited and perfectly matched lines. The numerical Laplace transform technique (NLT) is used as reference for the evaluations. It follows that the proper implementation of each fitting technique depends on various factors; the type of function being adjusted, the desired frequency range, an others. Moreover, one cannot guarantee that there is one of these techniques that will always yield the best fitting. The paper provides guidelines for selecting the most convenient one for a particular application.

Key words: Bode, Least-Squares, Vector Fitting, Levenberg-Marquardt, and Transmission Lines.

---

 

 

INTRODUCCIÓN

En varios campos de la ingeniería, para propósitos de análisis, diseño o simulación a menudo es necesario tener representaciones precisas de sistemas físicos con funciones de transferencia.

Específicamente, para el estudio de fenómenos electromagnéticos en sistemas eléctricos de potencia, los componentes deben ser modelados en un amplio rango de frecuencia. El problema de identificación en el dominio de la frecuencia se basa en la estimación de una función racional, con coeficientes reales (a_n, b_m) para ajustar una función compleja F(s) con la estructura algebraica mostrada en la ecuación (1).

Donde s es el vector de frecuencia compleja y usualmente n<m.

Existen diferentes procesos de estimación de parámetros para la ecuación (1). A continuación se presentan algunos antecedentes.En 1959 Levi [1] sugirió un procedimiento de linealización y presentó un método de ajuste para curvas en el dominio de la frecuencia. El método se basó en mínimos cuadrados y en el uso de derivadas parciales para minimizar el error cuadrático de una función.En 1963 Sanathanan y Koerner [2], utilizaron el método de Levi introduciendo un procedimiento iterativo. Consideraron el error como la diferencia entre las magnitudes de la función a ajustar y una función ajustada, esta última se representa como la relación de dos polinomios. Los coeficientes de los polinomios son el resultado de minimizar la suma del error al cuadrado.Por otro lado, J. R. Martí [3], presentó en 1982 un método basado en ajuste asintótico utilizando la técnica de Bode. Los parámetros de la aproximación son determinados automáticamente por la rutina, como una función de aproximación que “libremente” se adapta por si misma a la forma de la función aproximada.Más recientemente, Gustavsen y Semlyen en 1999 [4], desarrollaron una metodología general para el ajuste de respuestas en el dominio de la frecuencia. Conocida como Ajuste Vectorial o "Vector Fitting" se ha posicionado como una de las más populares para el ajuste racional. Esta técnica ha sido utilizada en diferentes campos de la ingeniería para el modelado de sistemas eléctricos [5-7]. Por otro lado, Noda [8], presentó en 2005 un algoritmo que particiona el rango completo de frecuencia para evitar el mal condicionamiento del sistema, además de utilizar una matriz de ponderación para mejorar iterativamente la aproximación. Este algoritmo ha sido utilizado en [9] para modelar el comportamiento de una línea de transmisión.
Por último, Pordanjani et al. [10], en 2011 propusieron un método basado en un algoritmo genético, el cual garantiza pasividad.

 

Técnicas de ajuste racional.

En esta sección se hace la descripción detallada de las técnicas de ajuste racional más utilizadas como son: Aproximación Asintótica de Bode, Mínimos Cuadrados Ordinarios, Mínimos Cuadrados Iterativamente Reponderados, Ajuste Vectorial y Levenberg-Marquardt.

Aproximación asintótica de bode.

La técnica por aproximación asintótica conocida como diagramas de Bode [11], fue introducida en 1945, y posteriormente aplicada por J. R. Martí [3], para el ajuste racional de modelos de líneas de transmisión. Los diagramas consisten en dos gráficas, una muestra cómo varía la amplitud de F(s) con la frecuencia y la otra muestra cómo lo hace el ángulo de fase. Para simplificar el desarrollo de la técnica se considera que todos los polos y ceros de F(s) son reales, distintos y de primer orden, así factorizando la ecuación (1) se llega a la ecuación (2).

Si se denota como (s = jω), entonces la ecuación (2) se representa como la ecuación (3),

Representando la función en su “forma estándar”, se tiene la ecuación (4).

Si se hace la asignación K₀=kz₁z₂---z_n/p₁p₂---p_m entonces la ecuación (4) en su forma polar se determina por la ecuación (5).

El método de aproximación asintótica solo ajusta la amplitud de la ecuación (5), la cual se expresa como, la ecuación (6).

La amplitud involucra multiplicación y división de factores asociados con los polos y ceros. Para reducir la ecuación (6) a sumas y restas de factores, ésta se expresa en términos de un valor logaritmo base 10, el decibel. Como su nombre indica, un decibel es la décima parte de un bel, escala utilizada por A. G. Bell para medir la ganancia de potencia en un sistema. Debido a que se tienen 10 decibeles en un bel, la relación de potencia en decibeles se define como: ver ecuación (7).

Como la potencia involucra valores de voltaje o corriente al cuadrado y asumiendo impedancias de carga y fuente iguales se tiene, la ecuación (8).

En la mayoría de las funciones de transferencia se utiliza la relación entre voltajes y/o corrientes. Por lo tanto, para el caso de la aproximación asintótica se utiliza la ecuación (8) para expresar la ecuación (6) en decibeles, como se indica en la ecuación (9).

Así, utilizando propiedades de logaritmos se tiene, la ecuación (10).

Para realizar el diagrama de la ecuación (10), se esboza cada término de forma separada y después se combinan las gráficas. En la expresión se pueden identificar 3 tipos de términos, la forma de aproximar cada uno de ellos se explica a continuación.

• Término 20log₁₀|K₀|- Este se aproxima con una línea horizontal debido a que  es constante.
• Término -20log₁₀|ω|- Este se aproxima con una línea recta de -20 dB/década, la cual hace intercepción con 0 dB en ω=1.
• Términos 20log₁₀|1+jω/z_n| ó -20log₁₀|1+jω/p_m|.- Sin considerar el signo, ambos términos tienen el siguiente comportamiento: 20log₁₀|1+jω/z_n|→0 si ω=0 -20log₁₀|1+jω/p_m|→20log₁₀|ω/z_n|  si ω → ∞

Es posible aproximar el segundo término por dos líneas rectas, asíntota de baja frecuencia y asíntota de alta frecuencia, respectivamente.
La asíntota de alta frecuencia que aproxima el término 20log₁₀|ω/z_n| tiene una pendiente positiva de 20 dB/década, esta recta hace intercepción con 0 dB en ω=z_n, este valor se conoce como "frecuencia de ruptura". Entonces, el término 20log₁₀|1+jω/z_n| se aproxima con dos líneas rectas de pendiente 0 y 20 dB/década, y análogamente el término -20log₁₀|1+jω/p_m| se aproxima con dos líneas rectas de pendiente 0 y -20 dB/década de acuerdo a la explicación anterior. La adaptación de este método para el ajuste racional consiste en su implementación numérica, comparando la función a ajustar con la suma de los segmentos de líneas rectas, e introduciendo un polo o un cero donde sea necesario, a fin de mantener la gráfica de la aproximación dentro de un margen de error establecido [3].

Mínimos cuadrados ordinarios

El cálculo de los coeficientes para los polinomios N(s) y D(s) en la ecuación (1),puede ser formulado como un sistema lineal de mínimos cuadrados multiplicando ambos miembros de la ecuación por el denominador. De esta forma se obtiene un sistema sobre determinado Ax=b. Donde el k-ésimo renglón de A y los vectores x y b están dados por: ver ecuación (11a), (11b), (11c).

En términos matriciales, dado un vector  y una matriz , se desea encontrar un vector , tal que el producto Ax sea la mejor aproximación de b. Dicho en otras palabras, el problema lineal de mínimos cuadrados se acerca a la optimización si se encuentra un vector x que en algún sentido sea la mejor aproximación entre Ax y b [12]. Así, se debe definir el sentido de cercanía es decir, la norma que mide el vector residual r. La norma más utilizada es la euclidiana (l₂). Así, la solución en mínimos cuadrados de la ecuación (11), es el vector x que hace de |r|₂=|b-Ax|₂ un mínimo, como se expresa en la ecuación (12).

La ecuación (12), es la función objetivo a minimizar. Como las normas no pueden ser negativas, minimizar una norma equivale a minimizar su cuadrado.

Ecuaciones normales

La propiedad más significativa del vector residual del problema de mínimos cuadrados es que está enteramente en el espacio nulo de la matriz A^T. En términos algebraicos, una solución x satisface la ecuación (13), [12]:

o bien la ecuación (14),

El sistema de ecuaciones dado por la ecuación (14) se conoce como de  ecuaciones normales. La matriz A^TA, es semidefinida positiva si y solo si las columnas de A son linealmente independientes. Las ecuaciones normales son siempre compatibles, es decir, existe siempre una solución para la ecuación (14) aunque A^TA sea singular [12]. La solución encontrada por las ecuaciones normales está dada por la ecuación (15).

La matriz A, formada de acuerdo con la ecuación (11a), generalmente está mal condicionada debido al amplio rango de frecuencia que s puede tomar. Por este mal condicionamiento, la técnica presenta un mayor error para valores pequeños del rango de frecuencia. Es posible mejorar el mal condicionamiento de la matriz realizando un escalamiento en sus columnas, éste consiste en la multiplicación de la matriz por una matriz diagonal D de acuerdo a la ecuación (16), [12]:

Donde |a_k|₂, es la norma euclidiana de la k-ésima columna de A. El sistema lineal Ax=b, ahora queda determinado por la ecuación (17):

Denotando como A' = AD y x' = D^-1x, se tiene la ecuación (18),

Se desea que los coeficientes (a_n, b_m) para los polinomios N(s) y D(s) en la ecuación (1), sean cantidades reales. Para resolver la ecuación (18), en este sentido, ésta se separa en sus partes real e imaginaria de acuerdo con la ecuación (19),

Donde los sub-índices r e i denotan las partes real e imaginaria respectivamente. Con lo anterior se asegura que los coeficientes (a_n, b_m) sean cantidades reales. Una vez que se obtiene la solución del sistema de ecuaciones dado por ecuación (19), se calcula el vector x que contiene los coeficientes de la función racional.

Mínimos Cuadrados Iterativamente Reponderados

El método se utiliza para resolver ciertos problemas de optimización, en los cuales, la función objetivo a minimizar está dada por la ecuación (20), [12]:

Donde W es una matriz diagonal de pesos, diag(w₁,w_m,...,w_m)>0. Las ecuaciones normales para el método se muestran en la ecuación (21):

La solución para la ecuación (21), está dada por la ecuación (22):

Es posible llevar la ecuación (22) hasta un procedimiento iterativo utilizando la estructura algebraica mostrada en la ecuación (23):

Donde i representa el número de iteración. En la solución iterativa de las ecuaciones normales ponderadas se deben tener en cuenta el escalamiento y las cantidades reales revisadas en la sección anterior. La matriz W, de acuerdo con la ecuación (23), se debe actualizar de forma iterativa. Para actualizar la matriz de pesos se debe considerar la función de error presentada en la ecuación (24):

Donde F̂(s_k,x) es la respuesta en frecuencia de la función racional identificada. Cada elemento de la matriz de pesos se actualiza de acuerdo con la ecuación (25):

Para el primer paso de iteración, W es la matriz identidad. Si la función objetivo a minimizar cumple con γ(x⁽ⁱ⁾)≤ γ(x⁽ⁱ⁺¹⁾), el vector x⁽ⁱ⁾ es la solución final.

Ajuste Vectorial

El Ajuste Vectorial o “Vector Fitting” es una metodología para el ajuste de respuestas en el dominio de la frecuencia con aproximaciones por funciones racionales. El ajuste se realiza reemplazando un juego de “polos de arranque o polos iniciales” por un juego de polos recalculados a través de un método iterativo [4]. La metodología realiza la aproximación en dos etapas, ambas con polos conocidos. La primera etapa comienza con la distribución de los polos iniciales, reales o complejos, sobre todo el rango de frecuencia de interés. En esta etapa un método iterativo mejora la posición de los polos. En la segunda etapa, una vez representado el sistema en fracciones parciales, se realiza el cálculo de los residuos en una sola iteración. Si se considera la aproximación racional dada por la ecuación (26):

Donde  c_n son los residuos, a_n son los polos, d es un término constante y h es un término proporcional. El problema del ajuste racional es encontrar todos los parámetros de la ecuación (26) para obtener una aproximación de F(s) sobre un rango de frecuencia dado. Se observa que la ecuación (26) corresponde a un sistema no lineal, debido a que a_n aparece en el denominador.

Identificación de los polos

El inicio de la metodología consiste en especificar un conjunto de polos de arranque ā_n en la ecuación (26). Además, se multiplica F(s) por una función desconocida σ(s). Por tanto es necesario introducir una función de aproximación para σ(s). Como resultado se tienen las ecuaciones (27) y (28).

donde: σF_fit(s) es el ajuste de σ(s)F(s) y σ_fit(s) es el ajuste de σ(s).

Si se despeja F(s) de la ecuación (27), se llega a la ecuación (29),

Ahora sustituyendo las ecuaciones (27) y (28) en la ecuación (29), se tiene la ecuación (30),

La ecuación (30), indica que los ceros de σ(s) son una aproximación de los polos de F(s), así el problema inicia con el cálculo de los ceros de la función auxiliar, σ(s). Se debe notar en las ecuaciones (27) y (28), que tanto la función de aproximación racional para σ(s) F(s) como la función para σ(s) tienen los mismos polos. Ahora multiplicando la ecuación (28) por F(s) se obtiene la ecuación (31):

Se igualan las ecuaciones (27) y (31), para obtener la ecuación (32):

Manipulando algebraicamente la ecuación anterior se llega a la ecuación (33),

La ecuación (33), indica que se tiene un problema no lineal donde F(s) depende de F(s). Una forma de solución adecuada es aproximar los polos mediante la determinación de los ceros de σ(s), los cuales se obtienen de . Así se utiliza el sistema de ecuaciones dado por la ecuación (33), planteándolo de acuerdo a la forma Ax=b, ver ecuación (34).

Donde cada termino se expresa de acuerdo a las ecuaciones (35a), (35b), (35c).

Representando la ecuación (35a), (35b), (35c), para un rango amplio de frecuencias se obtiene un sistema sobre determinado, finalmente se trabaja en cantidades reales de la misma forma que se plantea en la sección de mínimos cuadrados. La ecuación (34), expresada para un rango amplio de frecuencias, entrega como resultado un vector de residuos c̃ de la función auxiliar; el cálculo de los ceros de esta función corresponden a los valores propios de la matriz mostrada en la ecuación (36),

Donde A es una matriz diagonal que contiene los polos iniciales y b es un vector columna elementos unidad. c̃^T, es un vector fila que contiene los residuos de σ(s).

Identificación de residuos

Una vez que se han obtenido los polos para el ajuste, los residuos se pueden obtener resolviendo el problema original en la ecuación (26) empleando los ceros de σ_fit(s) como los nuevos polos a_n. Con esto se obtiene nuevamente un sistema lineal sobre determinado Ax=b, donde el vector solución es x=[c₁ --- c_N d h]^T , el cual se resuelve como la ecuación (34), donde la matriz ahora no tiene los términos negativos [4].

Método de Levenberg-Marquardt

Levenberg-Marquardt actúa más como el de gradiente descendiente (Apéndice A) cuando los parámetros están lejos de su valor óptimo, pero más como el de Gauss-Newton (Apéndice B) cuando los parámetros están cerca de su valor óptimo. Primero Levenberg y luego unos años más tarde Marquardt propusieron este método de acuerdo a la ecuación (37), [13]:

El término es una cantidad positiva. Es fácil notar que para valores pequeños de λ el método se comporta más como Gauss-Newton y para valores grandes de λ se parece más al método del gradiente. Por último, también se ha sugerido la modificación mostrada en la ecuación (38):

La solución a las ecuaciones normales para el método de Levenberg-Marquardt queda expresada en la ecuación (39):

Existen diferentes métodos de cálculo para λ. En [13], se realiza una revisión de los mismos; sin embargo el más común consiste en evaluar la función objetivo y, si γ(x+h)≤ γ(x) , entonces x es remplazado por x+h, y λ es reducido por un factor v. De otra forma λ se incrementa por un factor u sin actualizar x y el algoritmo continúa a la siguiente iteración.

Análisis de casos

Una función con dependencia frecuencial puede tener como origen una medición experimental. De esta forma se obtiene un modelo analítico a partir de esos datos. Otro origen puede ser una función analítica dependiente de la frecuencia, aquí la técnica remplaza a esa función analítica por una función racional. Esto es adecuado siempre y cuando la función racional sea más simple de resolver que la función original y se mantengan todas las características cualitativas y cuantitativas. Con el fin de explorar la precisión y versatilidad de las técnicas se presentan dos casos de estudio; el primero de ellos es ajustar una función analítica caótica. El segundo caso de estudio es analizar el efecto final en la simulación de un transitorio en una línea monofásica, aquí lo que se hace es ajustar la ecuación de los parámetros de la línea y remplazarla por una función racional [14-17].

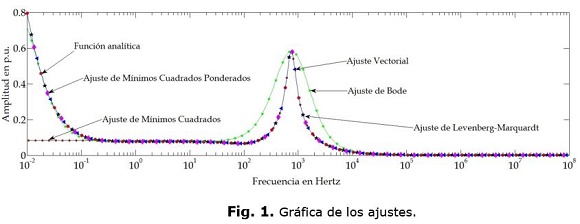
Caso de prueba 1

Para el primer caso se toma la siguiente función analítica de orden 5. Ver ecuación (40).

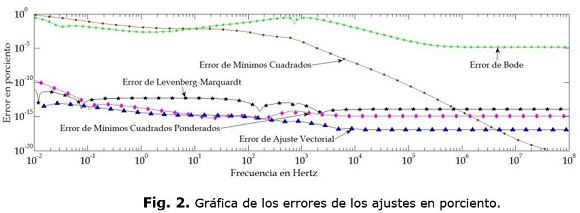
Se discretiza la función en el rango de frecuencias dado por ƒ=[1x10^-2 1x10⁸].Y se utilizan los 5 métodos descritos para realizar el ajuste de F(s). Cada uno de ellos arroja como resultado una función analítica distinta, la cual, dependiendo del método se tienen polos-ceros, coeficientes de polinomios o representación en fracciones parciales. La figura 1, muestra el comportamiento de todas estas funciones en comparación con la función original. Aunque en algunos casos las diferencias son relativamente pequeñas, la figura 2, muestra con claridad los errores porcentuales de cada ajuste utilizando la formulación de la ecuación (41):

Del análisis de resultados del ajuste de esta función analítica, se puede concluir que; Ajuste Vectorial, Mínimos Cuadrados Iterativamente Reponderados y Levenberg-Marquardt ajustan de manera adecuada esta función analítica, sin embargo cabe señalar que tanto Bode como mínimos cuadrados la ajustan adecuadamente por secciones; esta es la razón por la cual no es correcto concluir que unas técnicas son mejores que otras, sino que se concluye que para esta prueba específica unas técnicas son más adecuadas que otras. La tabla 1, muestra las funciones resultantes de cada ajuste.

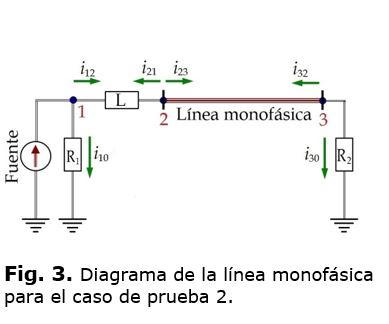
Caso de prueba 2

La simulación de un evento con simetría en un sistema de potencia, se puede hacer con su secuencia positiva en por unidad, es decir, como un sistema monofásico como el mostrado en la figura 3. Una longitud normal en un sistema de potencia es de 100 km, por lo tanto se utiliza esta longitud en la simulación. Los demás datos utilizados son: el radio del conductor es 0.0272 m, R₁=1.058 Ω es la resistencia interna del generador, L=70 mH es la inductancia interna del generador, R₂ es variable para representar la línea con terminación abierta, perfectamente acoplada o con terminación en corto circuito, la resistividad del terreno se toma como 100 Ω-m y la fuente como senoidal.
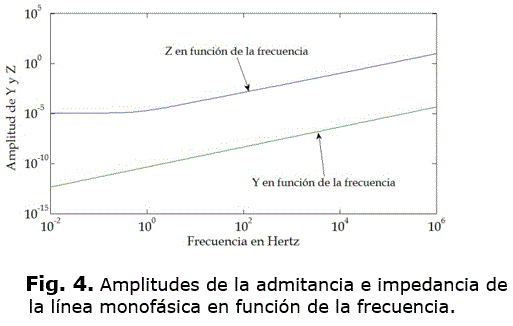
Para realizar esta simulación en dominio de la frecuencia, se sustituye Y y Z por sus modelos ajustados como funciones racionales del tipo dado por la ecuación (1). La figura 4, muestra el comportamiento de Y y Z en función de la frecuencia.

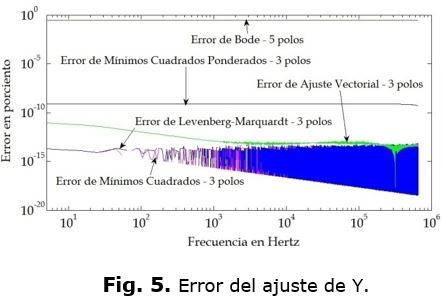
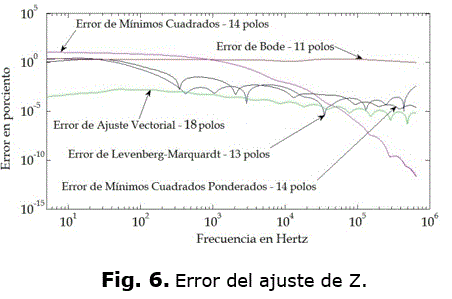
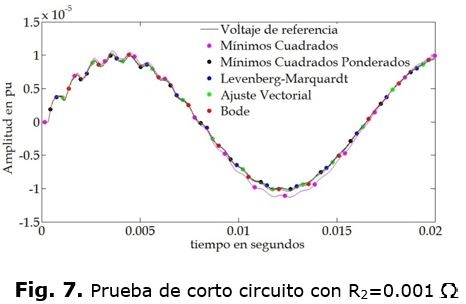
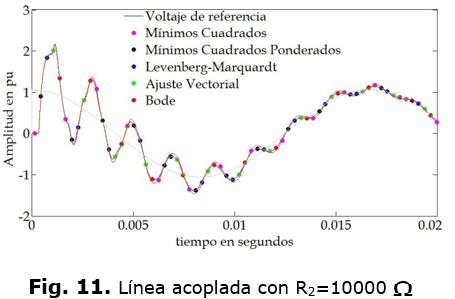
Las figuras 5 y 6, muestran los errores porcentuales de todas las funciones, en estas figura se nota con claridad cuál es el mejor o peor ajuste, lo cual no significa que para otra función se vayan a comportar de la misma manera. Los resultados obtenidos con los ajustes se comparan con los que se obtienen utilizando las funciones Y y Z originales. Se utiliza la transformada numérica de Laplace para realizar las simulaciones [18-20]. Los resultados se muestran en las figuras 7, 8, 9, 10, 11 y 12.

 

 

 

CONCLUSIONES

Aproximación Asintótica de Bode, Mínimos Cuadrados Ordinarios, Mínimos Cuadrados Iterativamente Reponderados, Ajuste Vectorial y Levenberg-Marquardt fueron descritos a detalle y aplicados en la identificación de parámetros para el modelado de sistemas eléctricos.
Dos casos de prueba fueron presentados para la evaluación de las técnicas de ajuste, primero se utilizaron para aproximar una función analítica, después se aplicaron en el ajuste racional de los parámetros Y y Z de una línea de transmisión monofásica.

Las principales conclusiones son las siguientes:

1. Para el caso del ajuste racional de la función analítica, se puede notar con claridad que dependiendo del perfil de la función a ajustar unas técnicas son más adecuadas que otras. Es decir, si la función analítica se presenta de la forma de las ecuaciones (1), (2) ó (26) esto incrementa o disminuye la complejidad para cada técnica.
2. En el caso del modelado de la línea de transmisión monofásica tres simulaciones en el dominio del tiempo fueron realizadas; línea en corto circuito, línea perfectamente acoplada y línea en circuito abierto. Analizando los ajustes para Y y Z, se puede notar que no siempre la misma técnica da el mejor resultado. También se concluye que el error en el ajuste para Y y Z se acarrea al error de la simulación en el dominio del tiempo (siendo para este caso específico menor para la técnica de Ajuste Vectorial). Sin embargo, debido a que esta técnica fue la que más polos utilizó para hacer el ajuste, la relación precisión-tiempo de ejecución no necesariamente será la más adecuada y siempre dependerá del usuario cuál de estas características tiene mayor peso.
3. A través de la aplicación de todas las técnicas fue posible obtener modelos para los parámetros Y y Z de la línea de transmisión, todos estos modelos mostraron su valía al presentar errores muy cercanos entre sí, esto fue posible determinarlo haciendo uso de la TNL.
4. Al final, y como punto final, no es posible determinar cuál técnica tendrá mejores resultados. Esto depende, entre otros factores, del tipo de función a ser ajustada, del grado del ajuste deseado, de la complejidad misma de la función, del rango de frecuencia deseado para el ajuste, del número de muestras usado e incluso de la precisión computacional.

Apéndice a – método del gradiente descendente

El gradiente de una función en un punto indica la dirección y sentido de la máxima variación de ésta en dicho punto. El método actualiza los parámetros en dirección opuesta al gradiente de la función objetivo. En este sentido, el gradiente de la función objetivo se expresa con la ecuación (42):

Si se asigna a la variable J, llamada Jacobiano, la función derivada parcial del lado derecho de la ecuación (42), se tiene la ecuación (43):

El Jacobiano representa la sensibilidad de la función a los parámetros x . Por lo tanto, la perturbación h calculada de acuerdo al método del gradiente que mueve los parámetros en la dirección descendente más pronunciada se calcula de acuerdo a la ecuación (44):

Donde por simplicidad se ha omitido la dependencia de las funciones.

Apéndice B – método de gauss-newton

El método supone que la función objetivo es cuadrática en relación a los parámetros cerca de la solución óptima. La función evaluada con los parámetros del modelo perturbado puede ser aproximada a través de la serie de Taylor de primer orden de acuerdo a la ecuación (45):

Por otro lado, la función objetivo a minimizar se expresa con la ecuación (46),

Donde por simplificación se omite la dependencia de las funciones. Sustituyendo la ecuación (45) en la ecuación (46) se llega a la ecuación (47):

La ecuación anterior muestra que γ(x) es aproximadamente cuadrática para la perturbación h y que el Hessiano para γ(x) es aproximado por J^TJ. La perturbación h que minimiza la función objetivo se encuentra con la ecuación (48a).

Donde la derivada de la ecuación (47) es la ecuación (48b):

Así, las ecuaciones normales para el método de Gauss-Newton están dadas por la ecuación (49):

Por lo tanto, la perturbación h calculada de acuerdo al método Gauss-Newton que actualiza los parámetros está dada por la ecuación (50):

 

 

REFERENCIAS

1. LEVY, E.C., "Complex curve fitting". IRE Transactions on Automatic Control, 1959, vol. AC-4, n.1, p. 37-44, Disponible en: doi: dx.doi.org/10.1109/TAC.1959.6429401, ISSN 0096-199X.

2. SANATHANAN, C.K.; KOERNER, J., "Transfer function synthesis as a ratio of two complex polynomials". IEEE Transactions on Automatic Control, 1963, vol.8, n.1, p. 56-58, Disponible en: doi: dx.doi.org/10.1109/TAC.1963.1105517, ISSN 0018-9286.

3. MARTI, J.R., "Accurate modeling of frequency-dependent transmission lines in electromagnetic transient simulations". IEEE Transactions Power Apparatus and Systems, 1982, vol. PAS-101, n.1, p. 147-157, Disponible en: doi: dx.doi.org/10.1109/TPAS.1982.317332, ISSN 0018-9510.

4. GUSTAVSEN, B.; SEMLYEN, A., "Rational approximation of frequency domain responses by vector fitting". IEEE Transactions on Power Delivery, 1999, vol.14, n.3, p. 1052-1061, Disponible en: doi: dx.doi.org/10.1109/61.772353, ISSN 0885-8977.

5. SCHNEIDER, H.; WEILAND, T., "Transient equivalent surface field excitations via rational approximation by vector fitting". En: International Conference on Electromagnetics in Advanced Applications (ICEAA). 2014, p. 44-47, Palm Beach: IEEE, Disponible en: doi: dx.doi.org/10.1109/ICEAA.2014.6903826, ISBN: 978-1479973255.

6. TANG M.; et al., "Time-Domain Modeling and simulation of partial discharge on medium-voltage cables by vector fitting method". IEEE Transactions on Magnetics, 2014, vol.50, n.2, p. 993-996, Disponible en: doi: dx.doi.org/10.1109/TMAG.2013.2283729, ISSN 0018-9464.

7. GORNIAK, P.; BANDURSKI, W., "A new universal approach to time-domain modeling and simulation of UWB channel containing convex obstacles using vector fitting algorithm". IEEE Transactions on Antennas and Propagation, 2014, vol.62, n.12, p. 6394-6405, Disponible en: doi: dx.doi.org/10.1109/TAP.2014.2359203, ISSN 0018-926X.

8. NODA, T., "Identification of a multiphase network equivalent for electromagnetic transient calculations using partitioned frequency response". IEEE Transactions on Power Delivery, 2005, vol.20, n.2, p. 1134-1142, Disponible en: doi: dx.doi.org/10.1109/TPWRD.2004.834347, ISSN 0885-8977.

9. NODA, T., "Application of frequency-partitioning fitting to the phase-domain frequency-dependent modeling of overhead transmission lines". IEEE Transactions on Power Delivery, 2014, vol.30, n.1, p. 174-183, Disponible en: doi: dx.doi.org/10.1109/TPWRD.2014.2329532, ISSN 0885-8977.

10. PORDANJANI I.R.; et al., "A method to construct equivalent circuit model from frequency responses with guaranteed passivity". IEEE Transactions on Power Delivery, 2011, vol.26, n.1, p. 400-409, Disponible en: doi: dx.doi.org/10.1109/TPWRD.2010.2080323, ISSN 0885-8977.

11. NILSSON, J.A.; RIEDEL, S.A., Electric circuits. 8a ed., Prentice Hall, 2008, p. 799-815, ISBN: 978-0131989252.

12. BJÖRCK, A., Numerical methods for least squares problems. 1a ed., Philadelphia: SIAM, 1996, p. 165-175, ISBN: 978-0898713602.

13. FAN, J., "The modified Levenberg-Marquardt method for nonlinear equations with cubic convergence". Mathematics of Computation, 2011, vol.81, n.277, p. 447-466, Disponible en: doi: http://dx.doi.org/10.1090/S0025-5718-2011-02496-8#sthash.CDCFAJOk.dpuf, ISSN 1088-6842.

14. RAMOS-LEANOS, O., et al., "A wideband line/cable model for real-time simulations of power system transients". IEEE Transactions on Power Delivery. 2012, vol.27, n.4, p. 2211-2218, Disponible en: doi: dx.doi.org/10.1109/TPWRD.2012.2206833, ISSN 0885-8977.

15. RAMOS-LEANOS, O.; NAREDO J.L., GUTIERREZ-ROBLES J.A., "An advanced transmission line and cable model in MATLAB for the simulation of power-system transients". En: Vasilios N. Katsikis, MATLAB - A Fundamental Tool for Scientific Computing and Engineering Applications. Croatia: InTech, 2012, Chapter 12, p. 269-304, Disponible en: doi: dx.doi.org/10.5772/2557, ISBN: 978-953-51-0750-7.

16. NAREDO J.L., et al., "Improving numerical performance of transmission line models in EMTP". En: Proceedings of the 9th International Conference on Power Systems Transients, IPST2011. 2011, Delft, Disponible en: http://www.ipstconf.org/papers/Proc_IPST2011/11IPST006.pdf.

17. SEMLYEN, A.; GUSTAVSEN, B., "Phase-domain transmission-line modeling with enforcement of symmetry via the propagated characteristic admittance matrix". IEEE Transactions on Power Delivery, 2012, vol.27, n.2, p. 626-631, Disponible en: doi: dx.doi.org/10.1109/TPWRD.2011.2180405, ISSN 0885-8977.

18. GOMEZ P., et al., "Accurate computation of transient profiles along multiconductor transmission systems by means of the numerical Laplace transform". IEEE Transactions on Power Delivery, 2014, vol.29, n.5, p. 2385-2393, Disponible en: doi: dx.doi.org/10.1109/TPWRD.2014.2313526, ISSN 0885-8977.

19. NURICUMBO-GUILLEN, R., "Computation of transient voltage profiles along transmission lines by successive application of the numerical Laplace transform". En: North American Power Symposium (NAPS). 2013, p. 1-6, Manhattan: IEEE, Disponible en: doi: dx.doi.org/10.1109/NAPS.2013.6666944.

20. ZHANG ZHONG, Y.; et al., "Modeling and calculation for conductive coupling caused by lightning over-voltage in substation based on numerical inverse Laplace transform". En: 2012 Asia-Pacific Power and Energy Engineering Conference (APPEEC), 2012, p. 1-4 Shanghai: IEEE, Disponible en: doi: dx.doi.org/10.1109/APPEEC.2012.6307361, ISBN 978-1457705458.

 

 

Recibido: Febrero de 2014
Aprobado: Diciembre de 2014

 

 

Eduardo Salvador Bañuelos Cabral: Centro de Investigación y Estudios Avanzados (Cinvestav), Guadalajara, México. e-mail: [e-mail]