Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Energética
versión On-line ISSN 1815-5901
Energética vol.39 no.3 La Habana sep.-dic. 2018
TRABAJO TEÓRICO EXPERIMENTAL
Programación óptima del mantenimiento preventivo de generadores de sistemas de potencia con presencia eólica
Optimum scheduling of generator preventive maintenance of power system with wind presence
Yorlandys Salgado Duarte, Alfredo Martínez del Castillo Serpa, Ariel Santos Fuentefría
Universidad Tecnológica de La Habana José A. Echeverría, Marianao, La Habana, Cuba.
RESUMEN
El objetivo del trabajo fue programar el mantenimiento preventivo de las unidades generadoras de un sistema de potencia con un modelo de optimización que minimiza el costo de operación y mantenimiento. Para modelar el costo de operación de las unidades se utiliza una función cuadrática y para el mantenimiento una función lineal, ambas dependen de la demanda del sistema. Las propuestas de programación y la combinatoria que garantiza el menor costo de operación en el predespacho económico de las unidades son generadas con un algoritmo de optimización por enjambre de partículas. La función multi-variable no-lineal con restricciones que resulta como objetivo se optimiza mediante un método de programación cuadrática secuencial Cuasi-Newton que aproxima la Hessiana en cada iteración por diferencias finitas. El trabajo muestra como el margen de reserva del sistema afecta la programación del mantenimiento preventivo de un sistema de potencia con presencia de fuentes no convencionales de energía.
Palabras clave: Mantenimiento preventivo; optimización; pre-despacho económico; sistema eléctricos de potencia.
ABSTRACT
The objective of the work was to program the generator preventive maintenance of a power system with an optimization model that minimizes the cost of operation and maintenance. A quadratic function is used to model the operation cost of the units, and for the maintenance a linear function, both depend on the demand of the system. The programming proposals and combinatorial that guarantee the lowest cost of operation in the unit commitment are generated with a particle swarm optimization algorithm. The nonlinear multi-variable function with constrained that results in the modeling is optimized by a Quasi-Newton sequential quadratic programming method that approximates the Hessian in each iteration by finite differences. The work shows how the reserve margin affects the scheduling of preventive maintenance of a power system with the presence of unconventional sources of energy.
Key words: Preventive maintenance; optimization; unit commitment; power system.
INTRODUCCIÓN
Mantenimiento preventivo (MP) es un conjunto de tareas preventivas a intervalos fijos predeterminados durante la vida operativa del sistema analizado, destinadas a mejorar su confiabilidad. Todos los sistemas tienen prescrito programas de mantenimiento establecidos por el fabricante para reducir el riesgo de fallo. Las actividades de mantenimiento preventivo en general, consisten en la inspección, limpieza, lubricación, ajuste, alineación, y/o reemplazo de componentes que se desgastan o fallan. Independientemente del sistema analizado, estas actividades preventivas se pueden clasificar de dos maneras: restauración o sustitución de componentes.
En los Sistemas Eléctricos de Potencia (SEP) las unidades generadoras son fundamentales para garantizar el servicio eléctrico. Cada una de dichas unidades tiene prescrito un procedimiento para ejecutar su MP, que, en cuestiones de planificación a nivel de sistema, se reduce al tiempo que demoran en ser realizados. La programación del MP de este sistema en particular consiste en una disyuntiva básica entre el costo de la realización de los mantenimientos y el ahorro del costo que se logra mediante la reducción de la tasa global de incidencia en los fallos del sistema. Los diseñadores de programas de MP pueden programar las tareas y conciliarlas a nivel de sistema teniendo en cuenta los costos individuales en un intento de minimizar el costo total de la operación y mantenimiento del sistema [1], o pueden estar interesados en maximizar la confiabilidad del sistema, sujeto a algún tipo de restricción presupuestaria [2]. Además de las dos propuestas de programación anteriores, actualmente existen criterios para programar el MP que consideran el Margen de Reserva (MR) teniendo en cuenta la disponibilidad y la satisfacción de la demanda como funciones objetivo [3], incluso ya existen modelos multi-objetivos que tienen en su formulación como objetivo un compromiso entre la confiabilidad y los costos, contemplándose en algunos casos el comportamiento del mercado de electricidad [4]. Sin embargo, los dos primeros mencionados son los más utilizados. Para cualquiera de los casos, el problema a resolver es encontrar la mejor secuencia de acciones en los MP para cada unidad generadora del SEP en un horizonte de planificación.
Por otro lado, es necesario destacar, que los objetivos y las restricciones de la programación del MP de las unidades generadoras de un SEP, no están tan bien definidos y son todavía un área de investigación, porque en general, los objetivos y las restricciones que se emplean para este problema en investigaciones previas han sido muy diferentes y dependen de las preocupaciones individuales de las empresas que comercializan la energía. Sin embrago, es un consenso que sea definido como un problema de optimización combinatorio multi-criterio de funciones objetivo no lineales con restricciones y que determinan el momento y la secuencia de los períodos de MP de cada una de las unidades generadoras, suponiendo que el tiempo de duración de estos son fijos [1-4]. Por tanto, el conjunto de variables x en un problema de programación del MP se representa implícitamente por el tiempo de inicio del MP para todas las unidades generadoras consideradas.
Para la realización de los MP en cada una de las unidades generadoras involucradas en el suministro de electricidad, se necesita que las mismas estén fuera de servicio, esto provoca la disminución de la capacidad estática y por consecuencia la disminución del MR. Este fenómeno afecta la operación del SEP por varias razones, conllevando a que la programación del MP debe ser coherente con la operación del sistema, por lo que, ya sea en los objetivos y/o en las restricciones, debe contemplarse esta relación.
Independientemente de cubrir la demanda eléctrica, el SEP debe proporcionar una capacidad de generación eléctrica adicional de reserva para garantizar el suministro de electricidad a los clientes en caso de una avería repentina en las unidades generadoras o altos picos inesperados en la demanda eléctrica. Este criterio ha sido incluido con éxito en modelos anteriores, ya sea con enfoques probabilísticos [5] o determinísticos [3]. El criterio utilizado en la investigación presentada es el segundo.
Los efectos visibles del cambio climático han contribuido a concientizar tanto en la sociedad moderna como en la comunidad científica la necesidad de utilizar fuentes no convencionales para la generación eléctrica, dígase el viento y el sol, y la mayoría de los ingenieros que planifican y operan estos sistemas tienen una comprensión práctica de sus potencialidades. Estas nuevas condiciones aumentan la versatilidad de la matriz energética, por lo que actualmente se realizan esfuerzos para incluirlas en los modelos actuales de programación del MP [6, 7]. El modelo propuesto incluye en la conciliación de la programación, un parque eólico con los MP de cada uno de sus aerogeneradores, brindando resultados importantes para la solución del problema con estas nuevas condiciones.
El modelo desarrollado en esta investigación sintetiza las ideas presentadas en los tres párrafos anteriores. Se propone un modelo para conciliar la programación del MP que tiene como función objetivo minimizar el costo total de operación y mantenimiento de las unidades generadoras del SEP. El modelo es capaz de incorporar el MR como restricción para garantizar una operación confiable teniendo en cuenta la presencia de fuentes no convencionales de generación (eólica) como parte de la matriz del sistema analizado. Mediante la función objetivo se establece una relación armónica entre la demanda eléctrica del sistema, la generación eólica y la capacidad de generación convencional a través del pre-despacho económico, y con la restricción MR se contemplan las posibles averías repentinas que pudiesen ocurrir en el sistema. Además, en la investigación se estudia como el MR utilizado como restricción para garantizar una operación confiable puede afectar la programación del MP de un SEP con presencia de fuentes no convencionales de generación.
MATERIALES Y MÉTODOS
Problema del Despacho Económico
El Despacho Económico (DE) es un proceso importante para la operación y planificación a corto plazo de un SEP. El objetivo de este problema es encontrar el costo mínimo de producción de potencia cuando se satisfacen las restricciones de igualdad y desigualdad del sistema. La forma simplificada de la función objetivo de este problema puede expresarse como la suma de las curvas de costo de operación de todas las unidades de generación del sistema, en este artículo se define la función objetivo en las ecuaciones (1) y (2), como sigue a continuación:
Donde Ci es el costo de operación de la unidad generadora i, que es función de la potencia Pi. Las variables αi, βi, γi, son las constantes de costos de la unidad generadora i, y NG es el número de unidades generadoras en el sistema analizado.
Para minimizar el costo total de operación del sistema, es necesario garantizar determinadas restricciones. Una de las más importantes es el balance de energía mostrada en la ecuación (3), la cual se introduce como una restricción de igualdad en el modelo, en este artículo se define como:
Donde L es la demanda total del sistema y PL son las pérdidas totales de las líneas de transmisión. Sin embargo, en este estudio las pérdidas de la red no son consideradas.
Por otro lado, cada unidad de generación tiene por diseño, un rango de potencia en el cual puede operar, esta restricción de desigualdad estaría dada por los límites máximos y mínimos de operación de la unidad como se muestra en la ecuación (4), en este artículo se define como:
Donde Pi,min es la potencia mínima de la unidad generadora i y Pi,max es la potencia máxima de la unidad generadora i.
El problema planteado, presenta una función objetivo no lineal multi-variable con restricciones. Para su solución, en esta investigación, se utiliza un método de Programación Cuadrática (PC) secuencial por las características de la función objetivo que resuelve un sub-problema de PC en cada iteración. Para estimar la Hessiana en cada iteración se usa la fórmula BFGS [8, 9], que es una generalización del método de la secante para el espacio multidimensional. Este método sustituye la primera derivada por su aproximación en diferencias finitas y puede incorporar restricciones simples del tipo li < xi < ui, siendo xi la variable Pi y li y ui los límites inferior y superior, que para el problema a resolver en esta investigación serían Pi,min y Pi,max.
Los SEP tienen la característica de poseer en la mayoría de los casos una matriz energética diversa y márgenes de reserva para garantizar estándares de confiabilidad en el sistema. Estas condiciones hacen que estén conformados por unidades con funciones de costo de generación disímiles y que existan más unidades generadoras que las necesarias para poder cubrir la demanda. Al poseer estas características, antes de ejecutar el DE, es necesario conciliar en un Pre-Despacho Económico (PDE), la combinación de unidades del sistema que entrarán en el DE, para garantizar de esta manera el menor costo total de operación para el sistema. Esta problemática se contempla en este artículo rescribiendo las ecuaciones (1) y (3) por las ecuaciones (5) y (6), como se muestra a continuación:
Donde Vi definida en la ecuación (7), es una variable binaria que toma valor 1 cuando la unidad generadora i está operando y toma valor 0 cuando la unidad generadora i está en estado de reserva por necesidad del sistema, quedando definida en este artículo como:
La reformulación del problema por las ecuaciones (5) y (6) en la investigación resulta, según la teoría de la complejidad computacional, en un problema NP completo (acrónimo en inglés de Nondeterministic Polynomial time). Por tanto, el PDE consiste en encontrar la mejor combinación de unidades de generación que garanticen el menor costo total de operación para el sistema. Las combinaciones que pueden generarse dependen de NG, considerando según la ecuación (7) que cada unidad puede estar en solo dos estados posibles, el espacio de búsqueda es del orden 2NG. Para solucionar esta problemática se utiliza en la investigación el algoritmo heurístico de optimización por enjambre de partículas (PSO, por sus siglas en inglés) basado en inteligencia de grupo propuesto por Kennedy y Eberhart en 1995 para la solución de los problemas de optimización. El algoritmo PSO ha sido aplicado satisfactoriamente a diferentes problemas que requieren la estimación de parámetros en espacios de altas dimensiones. Estas características son idóneas para la solución del problema de esta investigación, porque la cantidad de generadores de un SEP puede llegar a ser relativamente grande y por consiguiente también el espacio de búsqueda.
La solución del PDE mostrado en la ecuación (5), se obtiene generando con el algoritmo PSO para cada unidad de generación i un número aleatorio entre [0, 1], luego este valor es redondeado para obtener el Vi de cada unidad de generación i. La combinación generada en cada iteración del algoritmo PSO que cumpla con la restricción mostrada en la ecuación (8),
es evaluada mediante el DE y la solución del PDE es el menor valor de todas las evaluaciones hechas en la función objetivo de la ecuación (1). Las combinaciones que no cumplen con la ecuación (8), son desechadas por el algoritmo PSO mediante una función de penalización.
Problema del Mantenimiento Preventivo
Las unidades generadoras para garantizar su vida operativa, tienen prescrito un conjunto de tareas preventivas que, en la planificación a nivel de sistema se reflejan como el tiempo que demoran en realizarse. El MP de una unidad de generación es típico planificarlo en un año calendario, pero tiene el inconveniente que para ejecutarlo es necesario que la unidad este fuera de servicio. Estas dos condiciones inducen que para contabilizar el costo de estas tareas preventivas en un año calendario se utilicen en este artículo las ecuaciones (9, 10 y 11).
Donde δi es una constante que agrupa el costo fijo (horas/año) de realizar las tareas de mantenimiento, εi es un costo variable que depende de la potencia Pi que pudiese haber entregado la unidad generadora i si hubiese estado disponible en el DE, TTMi es el tiempo de inicio del mantenimiento de la unidad i, TDMi es el tiempo de duración del mantenimiento de la unidad i y Uit es una variable binaria que toma valor 1 cuando la unidad generadora i está operando en el instante de tiempo t, y toma valor 0 cuando la unidad generadora i está en mantenimiento en el instante de tiempo t.
Modelo del Parque Eólico
La capacidad instantánea de generación PWTt de un parque eólico en el instante de tiempo t está determinada por la Pit de cada aerogenerador i del parque. A diferencia de las unidades generadoras convencionales, la potencia Pit en este caso, es función del viento SWit. En la investigación se utiliza el modelo de Weibull [10] para modelar el viento, y en este artículo su función de densidad de distribución de probabilidad se define en la ecuación (12). Los parámetros forma y escala mostrados en las ecuaciones (13) y (14), respectivamente se estiman a partir de la velocidad media del viento µSW y su desviación estándar σSW con respecto a la media histórica del lugar donde se va instalar el parque.
A partir de conocer los parámetros de la ecuación (12), y con la inversa de la función de distribución de probabilidad acumulada mostrada en la ecuación (15), se puede simular el comportamiento de la velocidad del viento a partir de generar u números aleatorios uniformemente distribuidos entre [0, 1] como se muestra en la ecuación (16).
Una vez conocida la velocidad del viento en el lugar donde se pretende instalar el parque eólico, se puede estimar a partir de la relación funcional mostrada en la ecuación (17), la potencia que puede entregar cada aerogenerador.
Donde, Pr, Vci, Vr y Vco son la potencia nominal de salida, la velocidad del viento necesaria para el arranque, la velocidad del viento para la cual el aerogenerador alcanza su potencia nominal y la velocidad de viento de corte del aerogenerador respectivamente [11]. Las constantes A, B, y C definidas en las ecuaciones (18, 19 y 20), dependen de Vci, Vr y Vco tal como se expresan a continuación [11]:
La potencia que entrega el parque PWTt está dada por la ecuación (21).
Donde, NG es el número de aerogeneradores que tiene el parque y P(SWt) es la potencia que entrega cada aerogenerador.
Modelo de optimización
Los procesos de PDE y MP tienen una relación armónica. El MP es necesario para garantizar la vida operativa de las unidades de generación, pero tienen el inconveniente que al estar la unidad de generación fuera del sistema, se afecta notablemente la operación porque es una unidad que no va estar disponible en el PDE. Por tanto, es necesario contar con un criterio que permita decidir el momento del año donde es conveniente ejecutar las tareas de MP para cada una de las unidades de generación i, afectando lo menos posible la operación del sistema. La generalización del PDE para cada hora t permite conciliar ambos procesos y resultar en un modelo para programar del MP de las unidades generadoras de un SEP. El modelo propuesto tiene como función objetivo minimizar el costo total de operación y mantenimiento del sistema y en este artículo se define en las ecuaciones (22, 23 y 24), como se muestra a continuación:
Donde:
Cit es el costo de operación de la unidad generadora i en el instante de tiempo t, que es función de la potencia Pit.
Dit es el costo de mantenimiento de la unidad generadora i en el instante de tiempo t, que es función de la potencia Pit.
Uit es una variable binaria que toma valor 1 cuando la unidad generadora i está operando en el instante de tiempo t, y toma valor 0 cuando la unidad generadora i está en mantenimiento en el instante de tiempo t.
Vit es una variable binaria que toma valor 1 cuando la unidad generadora i está operando en el instante de tiempo t, y toma valor 0 cuando la unidad generadora i está en estado de reserva en el instante de tiempo t por necesidad del sistema.
Pit es la potencia que entrega la unidad generadora i en el instante de tiempo t.
αi, βi, γi, δi, εi constantes de costos de la unidad generadora i.
NG es el número de unidades generadoras en el sistema analizado.
NT es el número de horas t del horizonte de planificación analizado.
Las restricciones del modelo propuesto en este artículo se definen en las ecuaciones (25, 26, 27, 28 y 29), como se muestra a continuación:
Donde:
TTMi es el tiempo de inicio del mantenimiento de la unidad i.
TDMi es el tiempo de duración del mantenimiento de la unidad i.
Lt es la demanda total del sistema en el instante de tiempo t.
PWTt es la potencia que entrega el parque eólico en el instante de tiempo t.
MR es el margen de reserva necesario para el sistema (Constante equivalente a la capacidad de la unidad de generación más grande o margen impuesto por el sistema).
Pit, min es la potencia mínima de la unidad generadora i en el instante de tiempo t.
Pit, max es la potencia máxima de la unidad generadora i en el instante de tiempo t.
VP es el horizonte o ventana de planificación considerada.
En acápites anteriores se comenta el efecto que tiene el MR en el sistema y como se simula el comportamiento de un parque eólico. Para garantizar una operación con determinados estándares de confiabilidad, es usual prever con el MR el efecto que tendría para el sistema una avería inesperada en algunas de las i unidades de generación. La incorporación de este indicador en la ecuación (25) perturba la programación del MP porque limita el espacio de búsqueda del modelo de optimización propuesto en la investigación. En esta propia restricción se tiene en cuenta también el efecto de la potencia que entrega el parque eólico.
RESULTADOS Y(O) DISCUSIÓN
La investigación utiliza datos del sistema propuesto por el Subcomité de Aplicaciones de Métodos Probabilísticos del Instituto de Ingenieros Eléctricos y Electrónicos (IEEE-RTS) [12], desarrollado con el objetivo de proveer un sistema de prueba común para la aplicación de diferentes métodos. Este sistema posee 32 unidades generadoras con rangos de capacidad entre 12 y 400 MW. Tiene una capacidad instalada de generación de 3 405 MW y su demanda máxima es 2 850 MW.
En la presente investigación, de todas las unidades del sistema IEEE-RTS, solo se utilizan las que se relacionan en las tablas 1 y 2.


La capacidad instalada que resulta de considerar las unidades de las tablas 1 y 2 es de 164 MW. Para el caso de la demanda se utiliza el modelo en por unidad que brinda [12], pero la demanda máxima utilizada es 100 MW y se limita el horizonte de planificación (VP) al primer trimestre del año.
El parque eólico considerado en este estudio tiene una capacidad instalada de 20 MW, esto representa una presencia eólica por concepto de capacidad instalada de 10,87%. Para modelar la potencia que entrega cada aerogenerador se utiliza la ecuación (17), que está sujeta a las siguientes consideraciones:
-
Para simular el viento con el modelo Weibull se utilizan las ecuaciones (13) y (14) para estimar los parámetros forma y escala suponiendo que µSW = 5,42 m/s y σSW = 3,05 m/s.
-
El aerogenerador utilizado en esta investigación tiene una potencia nominal Pr = 2 MW, la velocidad del viento necesaria para el arranque Vci = 4,17 m/s, la velocidad de viento para la cual el aerogenerador alcanza su potencia nominal Vr = 10 m/s y la velocidad de viento de corte del aerogenerador Vco = 22,22 m/s.
Los valores de cada una de las variables relacionadas anteriormente para el parque eólico llamado Regina son tomadas de estimaciones reales [11]. Además, se considera que cada aerogenerador del parque tiene 2 semanas de MP en el trimestre analizado.
La investigación pretende evidenciar el efecto que tiene el MR en la programación del MP del sistema analizado; pero antes se verifican algunos de sus resultados parciales.
La tabla 3, muestra el comportamiento de los costos en el DE según la disponibilidad de las unidades generadoras, evidenciándose la importancia del PDE para obtener la mejor combinación de unidades disponibles para el cubrimiento de la demanda. El PDE desarrollado en esta investigación tiene en cuenta el costo de operación y el costo de mantenimiento, sin embrago, existen otros costos asociados a este que no se tienen en cuenta, estos son el costo de arranque y el costo de parada. El no tener en cuenta estos costos implica que se obtengan resultados en las combinaciones como los que se muestran en las dos últimas filas de la tabla 3, no obstante, esto no invalida los resultados obtenidos para la programación del MP porque como se observa en la figura 1, el PDE siempre llega a la solución óptima para cada hora analizada.


La figura 1 y la tabla 4, muestran tres propuestas evaluadas en la función objetivo y la solución óptima encontrada por el modelo, evidenciándose como según la distribución del MP de las unidades en el horizonte de planificación, el algoritmo es capaz de llegar a la solución que tiene los menores costos. La solución óptima encontrada mostrada en la figura 1, no considera el parque eólico, porque el comportamiento aleatorio del viento introduce variabilidades en las soluciones y no deja comprobar si el algoritmo llega siempre a la solución esperada.

El comportamiento del costo de operación y mantenimiento es proporcional a la demanda del sistema cuando están en funcionamiento las unidades que tienen los menores costos. Sin embargo, cuando estas están en mantenimiento, los costos se incrementan según la combinación resultante del resto de las unidades (ver figura 1).
Luego de verificar algunos resultados parciales, se pretende obtener los resultados finales del trabajo. El MR en este sistema tiene la función de garantizar los estándares de confiabilidad. En este problema se garantiza con un MR equivalente a la unidad más grande del sistema, en este caso 50 MW, respondiendo al criterio N – 1 utilizado como restricción de seguridad en los SEP. La introducción de esta restricción se refleja en el MP programado. La figura 2, muestra como esta obliga al modelo de optimización a programar el MP de las unidades de 50 MW en las últimas semanas del trimestre, porque es donde la demanda pronosticada es menor.

La figura 3 y la tabla 4, muestran los resultados que evidencian el cumplimiento del objetivo principal de la investigación, que es la programación óptima del MP de un SEP con presencia de generación eólica. La figura 3, muestra el proceso de convergencia del algoritmo en las últimas 25 iteraciones y la tabla 4, registra los resultados del modelo, es decir, los tiempos de inicio de mantenimiento para cada unidad generadora que conforma el sistema.


CONCLUSIONES
La investigación muestra principalmente que el costo de operación y mantenimiento estimado mediante el modelo propuesto es sensible a la integración de generación eólica y al MR definido para el sistema, y brinda un criterio técnico basado en costos que permite evaluar los posibles planes de MP de las unidades generadoras de un SEP con presencia de fuentes no convencionales. El algoritmo de optimización utilizado brinda una estimación eficiente coherente a las características de la función objetivo que modela el problema.
REFERENCIAS
[1].WANG, Yang; ZHONG, Haiwang; XIA, Qing; KANG, Chongqing; WANG, Tieqiang; CAO, Xin. “Coordination of generation maintenance scheduling and long-term SCUC with energy constraints and N-1 contingencies”. IET Generation, Transmission & Distribution, 2016, vol. 10, n. 2, p. 325-333. ISSN: 1751-8687. DOI: 10.1049/iet-gtd.2015.0183.Disponible en: http://ieeexplore.ieee.org/document/7407718/
[2].MANSHADI, Saeed; KHODAYAR, Mohammad. “Risk Averse Generation Maintenance Scheduling with Microgrid Aggregators”. Transactions on Smart Grid, 2016, vol. PP, n. 99, p. 1-1. ISSN: 1949-3053. DOI 10.1109/TSG.2017.2713719.Disponible en: http://ieeexplore.ieee.org/document/7944528/
[3].WANG, Yang; ZHONG, Haiwang; XIA, Qing; KIRSCHEN, Daniel; KANG, Chongqing. “An approach for integrated generation and transmission maintenance scheduling considering N-1 contingencies”. Transactions on Power Systems, 2016, vol. 31, n. 3, p. 2225-2233. ISSN: 0885-8950. DOI: 10.1109/TPWRS.2015.2453115.Disponible en: http://ieeexplore.ieee.org/document/7177142/
[4].WANG, Yang; KIRSCHEN, Daniel; ZHONG, Haiwang; XIA, Qing; KANG, Chongqing. “Coordination of Generation Maintenance Scheduling in Electricity Markets”. Transactions on Power Systems, 2016, vol. 31, n. 6, p. 4565-4574. ISSN: 0885-8950. DOI (10).1109/TPWRS.2016.2514527.Disponible en: http://ieeexplore.ieee.org/abstract/document/7387795/
[5].SUBRAMANIAN, S; ABIRAMI, M; GANESAN S. “Reliable/cost-effective maintenance schedules for a composite power system using fuzzy supported teaching learning algorithm”.IET Generation, Transmission & Distribution, 2015, vol. 9, n. 9, p. 805-819, ISSN: 1751-8687, DOI: 10.1049/iet-gtd.2014.0718.Disponible en: http://ieeexplore.ieee.org/document/7112896/
[6].GUOQIANG, Ji; WENCHUAN, Wu; BOMING, Zhang. “Robust generation maintenance scheduling considering wind power and forced outages”. IET Renewable Power Generation, 2016, vol. 10, n. 5, p. 634-641. ISSN: 1752-1416. DOI: 10.1049/iet-rpg.2015.0198.Disponible en: http://ieeexplore.ieee.org/document/7456543/
[7].MEZIANE, Rachid; BOUFALA, Seddik; HAMZI, Amar; AMARA, Mohamed. “Preventive Maintenance Optimization in Hybrid Solar Gas Power System using Gravitational Search Algorithm. Renewable and Sustainable Energy Conference (IRSEC), 2015 3rd International. Marrakech, Morocco, 2015. ISBN: 978-1-4673-7894-9. DOI: 10.1109/IRSEC.2015.7455130.Disponible en: http://ieeexplore.ieee.org/abstract/document/7455130/
[8].LOSHCHILOV, Ilya. “LM-CMA: An Alternative to L-BFGS for Large-Scale Black Box Optimization”. Evolutionary Computation, 2017, vol. 25, n. 1, p. 143-171. ISSN: 1063-6560. DOI: 10.1162/EVCO_a_00168.Disponible en: https://arxiv.org/abs/1511.00221
[9].QIL, Peng; ZHOU, Wei; HAN, Jizhong. “A Method for Stochastic L-BFGS Optimization”. Cloud Computing and Big Data Analysis (ICCCBDA), 2017 IEEE 2nd International Conference on. Chengdu, China. 2017. ISBN: 978-1-5090-4499-3. DOI: 10.1109/ICCCBDA.2017.7951902.Disponible en: http://ieeexplore.ieee.org/abstract/document/7951902/
[10].ATWA, Y. M.; EL-SAADANY, E. F.; SALAMA, M. M. A.; SEETHAPATHY, R.; ASSAM, M.; CONTI, S. “Adequacy Evaluation of Distribution System Including Wind/Solar DG During Different Modes of Operation”. IEEE Transactions on Power Systems, 2011, vol. 26, n. 4, p. 1945-1952. ISSN: 0885-8950. DOI: 10.1109/TPWRS.2011.2112783.Disponible en: http://ieeexplore.ieee.org/abstract/document/5732672/
[11].KARKI, R.; THAPA, S.; BILLINTON, R.. “A Simplified Risk-Based Method for Short-Term Wind Power Commitment”. IEEE Transactions on Sustainable Energy, 2012, vol. 3, n. 3, p. 498-505. ISSN: 1949-3029. DOI: 10.1109/TSTE.2012.2190999.Disponible en: http://ieeexplore.ieee.org/abstract/document/6194359/
[12].A report prepared by the Reliability Test System Task Force of the Application of Probability Methods Subcommittee (1999). The IEEE Reliability Test System-1996. IEEE Transactions on Power Systems, 1999, vol. 14, n. 3, p. 1010-1020. ISSN: 0885-8950. DOI: 10.1109/59.780914.Disponible en: http://ieeexplore.ieee.org/document/780914/
Recibido: 1/10/2017
Aprobado: 1/3/2018
Yorlandys Salgado Duarte, Universidad Tecnológica de La Habana José A. Echeverría, Marianao, La Habana, Cuba. E-mail: cmtysalgado@gmail.com; ysalgado@cemat.cujae.edu.cu













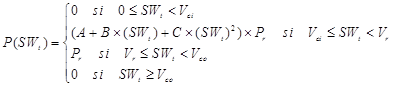 (17)
(17)
