ARTÍCULO ORIGINAL

 

 

Distribuciones Estadísticas para Modelar Clutter Marino: una Revisión

 

Statistical Distributions for Sea Clutter Modeling: A Survey

 

 

José Raúl Machado Fernández, Jesús de la Concepción Bacallao Vidal

Departamento de Telecomunicaciones y Telemática, Facultad de Telecomunicaciones y Electrónica, Universidad Tecnológica de la Habana "José Antonio Echeverría" (CUJAE), La Habana, Cuba.

 

 

---

RESUMEN

El clutter marino es una señal aleatoria interferente que aparece en lecturas de radar producto de la reflexión que experimenta la emisión sobre la superficie del mar. Luego de una intensa revisión sobre la literatura relacionada, se concluyó que existen 23 distribuciones estadísticas o modelos que pueden usarse para representar el clutter. Los autores clasificaron los modelos en cinco grupos diferentes atendiendo a la frecuencia de utilización y la relevancia de cada uno. La revisión realizada tiene dos logros fundamentales. Primeramente, se reunieron y unificaron las expresiones matemáticas de las distribuciones, lo que contribuye a la homogenización de los estudios. En segundo lugar, se ofreció un conjunto amplio de distribuciones candidatas para nuevas investigaciones relacionadas al ajuste de datos de lecturas de radar con modelos estadísticos. La investigación recomienda el empleo de 15 distribuciones, mientras que los estudios comunes rara vez utilizan más de cuatro.  

Palabras claves: Clutter Marino, Distribuciones Estadísticas, Distribución K, Log-Normal, Weibull.

---

ABSTRACT

The sea clutter is a random interfering signal that appears in radar readings caused by the reflection experienced by the emission over the sea surface. After a deep review on the related literature, 23 statistical distributions or models were found for representing sea clutter. The authors classified these models into five groups taking into account the frequency of use and the importance of each distribution. The performed review has two main achievements. Firstly, the mathematical expressions for the distributions were gathered and unified, which contributes to the homogenization of the studies. Secondly, a wide set of candidate distributions were offered enabling the execution of new investigations related to the fit of statistical distributions to empirical clutter data. The investigation strongly recommends the use of 15 distributions, while common studies rarely used more than four.       

Key words: Sea Clutter, Statistical Distributions, K distribution, Weibull, Log-Normal.

---

 

 

1.- INTRODUCCIÓN

 

La tarea de los radares primarios es detectar a los blancos dentro del área de observación y estimar su posición [1]. La detección sería una tarea fácil si los objetivos estuviesen ubicados en un medio no reflector, ya que los ecos captados en el receptor serían resultado exclusivamente de la retrodispersión de las ondas electromagnéticas, emitidas por el radar durante el sondeo, en la superficie del blanco. En tal caso, los ecos recibidos pudieran simplemente ser comparados con un umbral fijo, y los blancos serían detectados cuando sobrepasasen dicho umbral [2].

Sin embargo, en ambientes de operación reales aparece una señal interferente llamada clutter que se adiciona a la información del blanco y del ruido térmico, superando comúnmente la magnitud de este último [3]. El clutter es el resultado del rebote de la emisión del radar en el fondo donde está contenido el blanco. Dos de los fondos más comunes encontrados en aplicaciones operativas son el clutter marino y el clutter terrestre [4].

Los sistemas tradicionales de radar utilizan la detección lineal de amplitud [5] como la base de la percepción que tiene el instrumento sobre el ente medido. La mayoría de las investigaciones de radar usan este tipo de medición [6, 7] aplicando la siguiente operación sobre los componentes en fase (I, In phase) y en cuadratura (Q, In Quadrature):

No obstante, algunos sistemas, y consecuentemente algunos estudios, han sido desplegados usando mediciones de potencia o intensidad [8, 9].

Por muchos años, en radares de exploración terrestre de baja resolución, los ecos de clutter que forman las componentes individuales I y Q fueron interpretados como una distorsión gaussiana. En los radares modernos, que operan a bajos ángulos rasantes con alta capacidad resolutiva, se ha probado que la estadística del clutter se desvía de la característica Normal [8, 10-14]. Lo anterior significa que la distribución de la amplitud global Z ya no seguirá una distribución Rayleigh, que resultaría de la unión de dos variables aleatorias Gaussianas o Normales.

El clutter no-Rayleigh es catalogado en inglés con el término spiky o que tiene spikes. Los spikes son retornos de clutter de nivel mucho más alto que el promedio y que tienden a confundirse con blancos, provocando un incremento en la probabilidad de falsa alarma. Por ello, un problema de interés fundamental para la comunidad de radar es la modelación del clutter no-Gaussiano o no-Rayleigh para el diseño de detectores óptimos y subóptimos [15].

El clutter marino presenta frecuentemente aún más problemas con la aparición de spikes que el terrestre, por lo que los radares que operan en ambientes de mar tienen una seria limitación en su desempeño impuesta por los ecos indeseados [16]. Para corregir el problema de la discriminación entre fondo y blanco, múltiples distribuciones de probabilidad han sido propuestas para modelar el clutter [10, 13, 14, 17-22]. Los modelos más utilizados son el Log-Normal [11, 23], el Weibull [23, 24] y el K  [8, 16, 25-27].

1.1.   MOTIVACIÓN.

El grupo de radares del Departamento de Telecomunicaciones y Telemática de la Universidad Tecnológica de la Habana "José Antonio Echeverría" (CUJAE) comenzó a desarrollar soluciones enfocadas en la identificación de la estadística del clutter en [28]. El estudio de [28] recopiló 9 distribuciones, que modelan el clutter marino bajo condiciones climáticas y características de radar variadas, y las clasificó en tres grupos: distribuciones clásicas, compuestas y novedosas.

Pese a que la revisión efectuada fue adoptada con resultados satisfactorios, en [29] una versión diferente fue asumida para la distribución Weibull, señalándose así que la propuesta inicial no recomendaba la notación utilizada con mayor frecuencia. En efecto, las distribuciones a menudo son identificadas con igual nombre pero algunos autores utilizan fórmulas de Funciones de Densidad de Probabilidad (PDF, Probability Density Function) ligeramente diferentes, por lo que ciertas ambigüedades pueden aflorar en los estudios. Por ejemplo, la distribución K tiene al menos dos fórmulas de PDF global, una para la amplitud y otra para la intensidad [30].

Resumiendo lo planteado anteriormente, puede concluirse que un primer problema que afecta los desarrollos del grupo de radares de la CUJAE, y de la comunidad en general, es la variabilidad en la definición de las expresiones de cada distribución.

Adicionalmente, un segundo problema de las investigaciones internacionales, dedicadas al estudio del ajuste de distribuciones teóricas al clutter marino, es el hecho de que no todos los modelos son probados en cada ensayo. Mientras que la mayoría de los estudios clásicos se han enfocado en las distribuciones Log-Normal, Weibull y K [31-33]; otros tienen en cuenta una sola distribución [34-36] o un conjunto restringido de ellas [37-39]. El consenso generalizado parece ser el de

aceptar el modelo K compuesto como el que mejor representa el mar [40] y el Weibull como el más adecuado para clutter terrestre. La elección de la distribución K suele estar sustentada en la fundamentación física que ofrece el modelo [7]; si bien esta contradice la habilidad de la distribución K para ajustarse al clutter terrestre [30, 41]. Igualmente, ha sido probado el hecho de que para condiciones determinadas la Weibull puede superar a la K para el clutter marino [31] o ser superada a su vez por la Log-Normal para clutter terrestre [42].

Estos son solo algunos ejemplos de contradicciones existentes con respecto al tema. La solución podrá encontrarse a medida que más datos de radar estén disponibles al público [43] y sean puestas a competir las diferentes distribuciones cuando se ejecuten las mediciones correspondientes.

1.2.   OBJETIVO Y APORTES.

El presente estudio pretende contribuir a la solución de los dos problemas planteados anteriormente. Para ello, los autores se propusieron como objetivo realizar una revisión de las distribuciones que han sido usadas en la literatura para el modelado del clutter marino, sentando así una base teórica que puede ser asumida para realizar nuevos estudios de ajuste de distribuciones.

La clasificación efectuada dividió las distribuciones que han sido aplicadas al clutter en cinco grupos, donde el primero es el de uso más frecuente y más efectivo, y el último incluye modelos que tienen una fuerte tendencia al olvido o discontinuidad. Los grupos intermedios describen naturalmente una tendencia decreciente en la presencia en artículos científicos.

El presente artículo, expande la clasificación dada en [28] a un total de 23 distribuciones frente a las nueve enumeradas en la versión precedente. La posición otorgada a cada modelo, mostrada en la Figura 1, es justificada en cada caso con análisis basados en artículos recientes y clásicos de la literatura. Entre las 23 distribuciones encontradas, se recomienda el uso de las 15 primeras para la realización de estudios fiables sobre datos de radar. Sólo ejecutando experimentos con múltiples distribuciones de forma simultánea, se obtendrá una valoración adecuada del nivel de aplicación de cada una, descartándose así el resto.

 

2.   –CLASIFICACIÓN DE LAS DISTRIBUCIONES

 

Como puede apreciarse en la Figura 1, los grupos de distribuciones han sido denominados como: (1) Distribuciones Clásicas, (2) Distribuciones de Amplia Aplicación, (3) Distribuciones Reconocidas, (4) Distribuciones En Transición, y (5) Distribuciones Poco Usadas. Los tres primeros grupos reúnen las distribuciones principales, el cuarto aquellas que tienen posibilidades de adquirir relevancia y el último los modelos que están en desuso o han sido poco abordados. Las distribuciones del primer grupo son aquellas incluidas en la mayor cantidad de artículos y cuya aplicación ha sido validada por múltiples autores. El principal criterio para la ubicación de una distribución en la escala de clasificación mostrada en la Tabla 1 es el nivel de aplicación y las pruebas ofrecidas sobre su validación por distintos autores y variados conjuntos de datos. Adicionalmente, se tuvo en cuenta como un criterio secundario la cantidad de artículos encontrados en la literatura, que en su mayoría coincidía con el éxito de cada distribución. Por ejemplo, luego de una revisión de la literatura se encontraron 122 artículos para K, 65 para Weibull, 29 para Log-Normal, 26 para Rayleigh, 19 para Pareto, y así sucesivamente.

2.1.- GRUPO 1: DISTRIBUCIONES CLÁSICAS

Las distribuciones clásicas son aquellas que han sido usadas en la literatura tradicionalmente para la modelación del clutter marino, y que son incluidas comúnmente en entornos de simulación [29, 44]. Es muy difícil encontrar un artículo científico que considere el ajuste de los datos de clutter a varias distribuciones y no tenga en cuenta a la K [8, 16, 25-27], la Weibull [23, 24, 45] y la Log-Normal [11, 23]. Además, si bien es sabido que el clutter adopta formas no-Rayleigh para alta resolución y/o ángulo rasante bajo (condiciones encontradas frecuentemente), también es cierto que el modelo Rayleigh no ha dejado de ser usado. Esto es porque, aun reconociendo sus deficiencias, buena parte de los autores prueba el rechazo de la hipótesis Rayleigh como un primer paso cuando se aplican métodos de bondad de ajuste  [9, 31, 46, 47]. Conjuntamente, el modelo Rayleigh sigue siendo utilizado para modelar datos obtenidos a baja resolución. Además, gracias a su simplicidad matemática, la distribución es empleada para probar esquemas de detección de radar que no requieren de una representación exacta del eco recibido.

Distribución K.

La distribución K [8, 16, 25-27] es la preferida por la comunidad de radares para la modelación de los ecos de clutter marino a alta resolución (inferior a 30 metros) y ángulo rasante bajo (inferior a 5°). Múltiples estudios han demostrado que representa un ajuste razonable en un rango amplio de condiciones de clutter principalmente marino, además de ser capaz de representar los efectos de la agilidad de frecuencia (frequency agility) [8, 48-50]. De igual manera, la K  ha sido ajustada a mediciones de clutter terrestre para varias resoluciones, bandas de frecuencia y tipos de terreno [51-53]. La forma del modelo K  está entre las variantes Weibull y Log-Normal [23, 41].

Quizás su principal ventaja está en su definición compuesta que implica la interpretación del clutter marino como la unión de dos componentes: uno de variación lenta y otro de variación rápida [10]. Esta definición se corresponde con el mecanismo físico de generación de las olas del mar. La superficie marina está compuesta por dos tipos de olas: las capilares y las gravitatorias [54]. Así, el modelo K asume que una distribución, conocida generalmente como textura, representa las olas gravitatorias y otra, referida en inglés como speckle (capilaridad), simula la contribución de las olas capilares en la señal recibida.

Una segunda ventaja innegable de la distribución K es la gran cantidad de investigaciones dedicadas a ella que han contribuido a su enriquecimiento [55-59]. Modelos como el K más ruido térmico [60], el K-K [6] y el Generalizado K [61] han aflorado en intentos de complejizar la expresión original y hacerla extensible a multitud de situaciones de radar. Además, gracias a su formulación compuesta, la K tiene ventajas en cuanto a la simulación de las propiedades de correlación del clutter marino [62, 63]. 

La principal desventaja del modelo K es la intrincada definición de su PDF que incluye una función de Bessel, la cual hace que sea más difícil realizar cálculos con ella que con el resto de los modelos [42]. Aun así, la distribución sigue siendo utilizada como referencia en gran parte de los desarrollos recientes relacionados a clutter [64-68].

La PDF de la distribución K de la amplitud tiene la siguiente forma [69]:

Donde c es el parámetro de escala y v es el parámetro de forma que depende de las condiciones del mar y de las características del radar; por su parte K(.) es la función modificada de Bessel de segunda especie y de orden v-1.

Además, producto de su definición compuesta, la distribución tiene una versión diferente para el caso de las mediciones de potencia [69]:

De acuerdo a lo planteado por distintos autores [6, 13, 61], el parámetro de forma de la distribución K puede variar entre 0,1 y 30, según el carácter de las mediciones.

Distribución Weibull.

El modelo Weibull es muy versátil, ha sido aplicado para clutter terrestre [22, 53, 70], marino [39], atmosférico [42] y de hielo [71]. La distribución Weibull, al igual que la K, sirve como base a otros modelos como el Log-Weibull [72] y el Weibull-Weibull [6]. Además, su utilidad se maximiza para ángulo rasante bajo, alta resolución y entre las frecuencias de 1 y 10 GHz.

Aunque generalmente se asume que la distribución K modela mejor el clutter de mar, varias investigaciones dan ventaja a Weibull [6, 34, 39, 42]. Adicionalmente, la convergencia hacia la distribución Rayleigh, utilizada para baja resolución, es más suave en el caso Weibull, ocurriendo de forma natural cuando el parámetro de forma es igual a dos. En cambio, para la distribución K ocurre cuando el parámetro tiende a infinito [13, 73], lo que puede asumirse generalmente cuando v > 30 [30]. Este límite confuso hace que el parámetro de forma K incremente su varianza por el incremento del propio parámetro, haciéndose dificultosa la creación de soluciones de estimación paramétrica [74, 75].

Precisamente, una de las principales ventajas del modelo Weibull es su facilidad de simulación. Las variables aleatorias Weibull pueden generarse de forma sencilla utilizando el método de inversión [76]. La definición de la PDF Weibull no presenta complejidades, propiciando la derivación de soluciones sencillas en diversas situaciones de radares [30, 77]. Conjuntamente, los momentos de la distribución Weibull son manejables, con una función Gamma implementada en la mayoría de las herramientas matemáticas sin un costo computacional demasiado elevado. Todas estas ventajas de simulación han permitido que la distribución Weibull sea un modelo preferencial para nuevas implementaciones en campos como la inteligencia artificial [71, 78, 79].

Lo contrario ocurre para el modelo K que asume una definición compuesta precisando la generación de dos variables aleatorias, además de incluir una función de Bessel, cuyas dificultades de derivación pueden limitar la implementación de los sistemas.

La PDF de la distribución Weibull puede tomarse de [80] donde se usó:

Siendo α el parámetro de escala y β el de forma. La mayoría de las situaciones de clutter marino pueden ser modeladas variando el parámetro de forma en el rango entre 0,5 y 6,25 [6, 22, 39, 47, 53, 61, 81].

Distribución Log-Normal.

El modelo Log-Normal [11, 23] es casi tan reconocido como el Weibull y el K, pero su ajuste a los datos ocurre generalmente para condiciones más específicas que los otros dos. La convergencia de la CDF (Cumulative Distribution Function, Función de Distribución Acumulativa) Log-Normal es más lenta que la de las CDF Weibull y K, o lo que equivalente, su PDF es de cola más alargada [30]. Esto hace que el modelo Log-Normal  sea usado especialmente para modelar clutter muy spiky (donde los máximos de la señal de fondo ocurren más frecuentemente y tienen mayor magnitud).

La distribución Log-Normal es usada ampliamente tanto para clutter marino [31, 33, 42, 81] como para clutter terrestre [22, 30, 82]. Si bien en ocasiones se logra que el modelo prevalezca para una conjunto de mediciones de ángulo rasante bajo [42, 83], su mejor ajuste se logra generalmente para sub-conjuntos de datos de polarización HH [41], en la medición de la distribución espacial de los datos [30], y para celdas conteniendo reflexiones mezcladas de blancos y clutter [39, 42].

A pesar de su utilidad, la incapacidad del modelo de reducirse a la distribución Rayleigh lo hace menos atractivo para simulaciones de clutter [84]. No obstante, es usado como base para investigaciones relacionadas a detección de blancos [85].

En  [37, 38] se usó la siguiente expresión para la PDF de la Log-Normal:

Donde μ y  σ son los parámetros de escala y forma respectivamente. 

La expresión de la distribución Log-Normal dada en (27) no sufre variaciones significativas en los artículos científicos de la mayoría de los autores. En [32] solo se alteraron las letras usadas en la definición de los parámetros. Conjuntamente, en [70] el único cambio fue usar un parámetro de forma "inverso" dado por δ = 1⁄σ_N. Por el contrario, las distribuciones K y Weibull sí suelen sufrir transformaciones en su definición al pasar de un autor a otro, por lo que es importante revisar la expresión de PDF utilizada cuando se verifique un artículo científico.

Por último, tras revisar la literatura se comprobó que una variación del parámetro de forma (σ) entre 0,025 y 1,25 cubre la mayoría de las condiciones de operación [41, 53, 61, 82].

Distribución Rayleigh.

La  Rayleigh  se  gana  su  lugar  dentro  del  grupo  1  de  las distribuciones clásicas por su amplia aplicación como modelo

efectivo para baja resolución. Además, su desacuerdo con los datos experimentales de amplitud para alta resolución es verificado frecuentemente como un paso inicial de investigaciones más complejas [9, 32, 33, 46].

La Rayleigh fue el modelo concebido originalmente para el clutter de baja resolución, por ejemplo en [10] se encontró que el ajuste para Rayleigh era bueno para resolución de 150m. Sin embargo, los sistemas actuales son en su mayoría de alta resolución [86]. El modelo Rayleigh representa un clutter speckle-like (parecido a la capilaridad del mar) pero se aleja de situaciones donde el clutter es spiky (tiene saltos bruscos de amplitud) [13].

Desde un punto de vista matemático, el problema de la distribución Rayleigh está en su incapacidad de adaptar su forma a los resultados cambiantes medidos en ensayos empíricos para condiciones variadas. Esto es debido a la forma simple de su PDF que cuenta con un solo parámetro, cuya variación modifica de manera limitada la forma de la distribución. Modelos como el Weibull y el K pueden ser interpretados como extensiones complejizadas de la Rayleigh, pues se reducen a ella para cierta configuración de sus parámetros.

El PDF de la distribución Rayleigh puede tomarse de [47] donde se usó:

Siendo x el valor de la amplitud, y α el parámetro de escala y único de la distribución. Vale la pena resaltar que el modelo Rayleigh es frecuentemente empleado en desarrollos novedosos gracias a su simplicidad [87, 88].

2.2.- GRUPO 2: DISTRIBUCIONES DE AMPLIA APLICACIÓN

Luego de haber presentado las distribuciones del grupo 1 en el apartado anterior, el presente se dedica al grupo 2. El mismo fue denominado como distribuciones "de Amplia Aplicación" dado que son empleadas con frecuencia relativamente alta en investigaciones de clutter y su efectividad está probada en múltiples publicaciones. Las integrantes de este grupo son la Pareto, la Compuesta Gaussiana, la K-K y la K más ruido.

Distribución Pareto.

A la cabeza del grupo dos está la distribución Pareto [89] que se ha venido desarrollando en años recientes, superando a la variante K-K. En [90] se comprobó la efectividad de su ajuste para clutter marino, encontrándose que logra gran precisión para colas largas con la ventaja de solamente requerir dos parámetros y tener una definición más simple que la K-K. De hecho, su formulación compuesta es muy similar a la K, excepto que ahora el componente subyacente es modelado por una distribución exponencial negativa. Dada la relativa simplicidad del modelo, múltiples autores han sugerido el desarrollo de detectores simples de radar basados en la distribución [91, 92].

El modelo Pareto apareció por primera vez en análisis de radar en [93], en el contexto del modelado de clutter como una distribución Compuesta Gaussiana con textura Gamma Inversa. Adicionalmente, su validez fue reafirmada en [91] donde se le empleó como modelo para la distribución de la intensidad. La distribución de Pareto se caracteriza por tener una cola muy larga, y ha podido ser validada para radar de Banda X [94], y para ángulos rasantes altos [95]. En [95] se encontró también que la distribución de Pareto proporcionaba un mejor ajuste que la K-K y la K.

En [91, 96-98] se investigaron detectores coherentes usando tanto la distribución K-K  como la distribución de Pareto. Los trabajos mostraron que la forma del detector óptimo K-K es extremadamente complicada y no es viable de aplicar en un sistema real de radar, mientras que el detector de Pareto es mucho más simple. Conjuntamente, varios esquemas de detección coherentes, basados en el modelo de intensidad Pareto han sido analizados en varios artículos recientes [99-101]. También, desde la perspectiva incoherente, en [102] se abordan los integradores clásicos.

Otro aporte interesante aparece en [103] donde se emplea una relación entre las distribuciones Exponencial y Pareto para generalizar expresiones de detectores CFAR. En [104] se extienden los detectores introducidos en [103], siendo la motivación el desarrollo de detectores CFAR mejorados para la detección de blancos cuando las celdas de referencia contienen blancos interferentes.

Una combinación de la distribución Pareto-Pareto [105] ha sido también estudiada, pero se encontró que no ofrecía beneficios significativos en comparación con la versión individual. Por último, también existe un modelo Pareto más ruido [106] que aún cuenta con poca validación.

La distribución de intensidad Pareto [107, 108], con parámetro de forma α > 0 y parámetro de escala β > 0 tiene como PDF:

La distribución de Pareto es además aplicada a muchos otros fenómenos más allá del ámbito de los radares. En general, es una distribución que constituye un excelente modelo para fenómenos de cola larga [109]. Su aplicación original fue en la modelación del salario de una población [110]. A la par, ha sido empleada para modelar diferentes tipos de variables económicas [111] y en otras áreas como la física, la hidrología y la sismología [109]; así como aplicaciones vinculadas a la ingeniería como la modelación del teletráfico en Internet [112].

La amplia literatura presentada justifica la inclusión de este modelo en el grupo dos y sugiere fuertemente su ascenso al grupo uno. Los autores decidieron no colocarla en dicho primer grupo dado su relativamente corto tiempo de aplicación en ámbitos de radares. Otras distribuciones han dado a los investigadores un mayor tiempo para rebatir su validez.

Consultando las investigaciones de [104, 113, 114], se concluyó que el intervalo de 2 ≤ α ≤ 10 es el más adecuado para la representación del clutter marino. Simulaciones adicionales que fueron ejecutadas permitieron verificar que las muestras correspondientes a α < 2 producían magnitudes elevadas con demasiada frecuencia, mientras que aquellas pertenecientes a α > 10 desplegaban una cola muy corta en la PDF.

Distribución Compuesta Gaussiana.

La distribución Compuesta Gaussiana logra un buen ajuste para datos de bajo ángulo de rasancia, al igual que la K y la Weibull. La Compuesta Gaussiana asume que la envolvente compleja del clutter puede ser escrita como el producto de un componente rápido y uno lento [93, 115]:

El componente rápido x(t) = x_I(t) + jx_Q(t) conocido como speckle, tiene en cuenta la dispersión local y se asume como un proceso Gaussiano estacionario de media cero y potencia igual a la unidad; donde x_I(t) y x_Q(t) son las componentes en fase y en cuadratura respectivamente. El factor τ(t)es un proceso aleatorio real no-negativo, usualmente llamado la textura, que describe las variaciones de la potencia local reflejada debido a cambios en el área iluminada.

En las mediciones de amplitud de [35, 116-118] se usó textura Inversa Gamma [116, 117], cuyo PDF se muestra a continuación con parámetro de forma α y parámetro de escala β, donde Γ(.) denota a la función Gamma:

Adicionalmente, en [93] se dio una fórmula cerrada, que simplifica los cálculos, para el PDF de la Compound Gaussian (Compuesta Gaussiana) con Textura Inversa Gaussiana:

También en [93] fue demostrada la superioridad del ajuste Compuesto Gaussiano para un conjunto de datos de polarizaciones VV, HH, VH. Además, una aplicación del modelo Compuesto Gaussiano al desarrollo de mecanismos novedosos de detección puede encontrarse en [119]. Todo parece indicar que con el tiempo esta distribución cobrará mayor uso por lo que es una candidata fuerte a incluirse en el Grupo 1 de las distribuciones Clásicas. Referencia adicional sobre la distribución puede encontrarse en [61, 93, 115, 120-130].

Distribución K-K.

La distribución K-K, como su nombre lo indica, se deriva directamente de la distribución K. De hecho, el PDF es el resultado de la suma de dos variables K.

La K-K fue propuesta en [6] en un intento por mejorar el ajuste K en la zona de la cola para datos de clutter marino HH. Anteriormente, se utilizaba una distribución K-A con este propósito, pero la K-K demostró estar más cercana a los datos experimentales a la vez que tenía una PDF, aunque no del todo sencilla, menos costosa computacionalmente que la de K-A, que no tiene una forma cerrada.

Al igual que la Pareto y la K-A, la K-K se usa para clutter de ángulos rasantes medios y altos, que se vuelven spiky cuando mejora la resolución por distancia [6]. La recolección de datos para ángulos rasantes por encima de diez grados ha sido reportada en [6, 131, 132] para diversas polarizaciones y resolución de 0,75m.

La PDF de la amplitud K-K es [6]:

Donde f₁(x;v,σ) y f₂ (x;v_sp,σ_sp) son dos distribuciones K con parámetro de forma v e intensidad media σ para el componente de Bragg/Whitecap y v_sp y σ_sp para el componente de spike. El factor k determina la contribución relativa de los spikes al retorno global del clutter. Si k = 0, f(x) = f₁ (x;v,σ) y la distribución se simplifica a la K original. Importantes contribuciones al desarrollo de la distribución fueron hechas en [96, 97, 133-137].

Distribución K más ruido.

La distribución K más ruido térmico es una extensión del modelo clásico K, concebida para incluir la influencia del ruido externo al clutter. Luego de la propuesta inicial de la distribución en [16], una de las primeras referencias notables aparece en [41] donde, usando el radar IPIX de la universidad de McMaster de Canadá, se comprueba que las muestras de polarización cruzada de clutter contienen un componente gaussiano adicional debido al ruido térmico. Conjuntamente, la importancia de la aplicación de la versión que incluye ruido es señalada en [16] y el modelo ha sido incluido en varias investigaciones de ajuste de distribuciones como es el caso de [60]. Estimaciones precisas de los parámetros pueden ser obtenidas por el método desarrollado en [138].

La PDF para el clutter distribuido K más ruido está dado por [7]:

Donde p_n es el ruido térmico en el receptor, x es la intensidad local media, v es el parámetro de forma y b el de escala. Además, una versión para las mediciones de amplitud fue usada en [60] donde 2σ² es la potencia del ruido:

La distribución K más ruido térmico, si bien es más completa que la K original, tiene la limitación de no contar con una expresión cerrada de la PDF. Este hecho ha limitado hasta el momento su rango de aplicación. Contribuciones relacionadas a la distribución han sido presentadas en [67, 139-143].

2.3.- GRUPO 3: DISTRIBUCIONES RECONOCIDAS

El grupo 3 de las Distribuciones Reconocidas contiene distribuciones manejadas con regularidad dentro de la comunidad de radares pero que no han demostrado aún su superioridad con respecto a las tratadas en apartados previos. Este grupo cierra la categoría de los modelos más empleados por los diversos autores. Los grupos cuatro y cinco contienen distribuciones que no son de uso frecuente. El tercer grupo está compuesto por los modelos Generalizado K, Generalizado Gaussiano y K-A.

Distribución Generalizada K.

La distribución Generalizada K fue abordada en [61] donde, luego de comparar los datos disponibles con varios PDFs teóricos, se concluyó que proporcionaba el mejor ajuste, superando a la K original. El modelo cuenta con un parámetro de forma v y dos parámetros adicionales μ y b. Su PDF es presentado a continuación [61, 144]:

Nótese que cuando b = 1 el modelo se reduce al K tradicional con textura Gamma. Una extensión interesante del modelo se presenta en [145] donde se propone una alternativa denominada Bivariate Generalized-K (K Bivariada Generalizada).

Aunque no ha sido ampliamente probado, el modelo generalizado K es un intento por expandir la K clásica, por lo que podría ser una alternativa prometedora. Adviértase que el modelo hereda todas las ventajas de la K con el bonus adquirido de ser capaz de adaptarse a un mayor rango de condiciones gracias a la inclusión de un nuevo parámetro. No obstante, cuenta con el inconveniente de no tener una expresión cerrada para la PDF.

Distribución Generalizada Gaussiana.

La distribución parte de la Compuesta Gaussiana que asume dos contribuciones diferentes, una de variación lenta y otra de variación rápida conocida como speckle (capilaridad). La Compuesta Gaussiana se basa en la suposición de que el teorema del  límite  central  es  aplicable  y  asume  una estadística Normal para las componentes I y Q [36]. Se espera que cuando la resolución de la celda sea más pequeña que un cierto límite, el speckle se desvíe de la estadística Gaussiana, dado que el teorema del límite central no será ya aplicable. Este límite ha sido reportado en los 120 metros por resolución de azimut y 4 metros por resolución de distancia [146], aunque los valores propuestos podrían no ser definitivos.

Para sobreponerse a este problema, una versión más generalizada fue sugerida: el modelo Generalizado Gaussiano [146, 147], en el cual se asignan PDFs generales y multiparamétricos tanto al speckle como a la textura. El PDF global de la distribución Generalizada Gaussiana está dado por:

Con parámetros de forma β y b, y un parámetro de escala α.

Análisis sobre datos empíricos de clutter revelaron en [34] que el mejor ajuste global de los datos era Weibull y Generalizado Gaussiano para toda la distancia examinada. Esto sugiere el uso de la distribución como un modelo principalmente para clutter de bajo ángulo rasante.

Finalmente, aunque el modelo Generalizado Gaussiano engloba al Compuesto Gaussiano, el segundo es más frecuentemente utilizado en investigaciones actuales, lo cual justifica que tenga un nivel superior en la clasificación.

Distribución K-A.

La distribución estándar compuesta K asume que la intensidad media subyacente modula un componente speckle Gaussiano, apropiado para la dispersión tradicional que ocurre en las olas capilares. Este modelo no se aplica cuando spikes whitecap (picos de cresta de ola) espacialmente estrechos son observados [148, 149]. Una aproximación al modelado de ese tipo de spikes es la distribución K-A [150]. Ella ha probado representar con éxito clutter real con spikes discretos cuando se usa agilidad en frecuencia pulso-a-pulso [149] y ser efectiva para clutter de mar, particularmente para polarización HH [6].

En la distribución K-A, los dispersores tradicionales siguen una distribución K, y los spikes discretos son asumidos como pertenecientes a una distribución Poisson [149].

Hay cinco parámetros en la distribución K-A. Ellos son σ_n, σ_sp, σ_bw, y v. Esto, sumado a la no existencia de una expresión cerrada de la PDF, impone límites en la aplicación de la distribución que ha sido reemplazada por la K-K y la Pareto en los últimos años. No obstante, su presencia en la literatura aún es más fuerte que la de las distribuciones de los grupos cuatro y cinco. Podría decirse que la K-A es una candidata a caer del grupo 3.

2.4.- GRUPO 4: DISTRIBUCIONES EN TRANSICIÓN

Las distribuciones del grupo 4 están "en transición", o sea, que su estado final no ha sido aún definido: pueden devenir reconocidas o caer completamente en desuso. Es preciso señalar que las cuatro primeras del grupo son las que parecen tener mayor probabilidad de volverse "Reconocidas" mientras que el resto muestra una tendencia hacia el olvido. De cualquier forma, es beneficiosa la inclusión de estas distribuciones en análisis de ajuste de clutter ya sea para descartarlas completamente, o para resaltar su utilidad.

El cuarto grupo es el más amplio con 8 alternativas: Log-Weibull, Tsallis, Rician Inversa Gaussiana, Weibull-Weibull, Generalizada Gamma, Pearson, Generalizada K con Textura Log-Normal y Log-Normal Tri-paramétrica.

Distribución Log-Weibull.

La distribución Log-Weibull lucha fuertemente por ascender al grupo 3. El modelo propone una variante alternativa a la Log-Normal ya que ambas son consideradas aptas para clutter muy spiky que aparece comúnmente para ángulos rasantes muy bajos, polarización HH o muy alta resolución. El modelo Log-Weibull ha superado en ocasiones al Log-Normal en estas situaciones [151], aunque para sacar conclusiones definitivas son necesarios más experimentos. La distribución Log-Weibull ha sido utilizada con éxito para realizar ajustes sobre datos de clutter terrestre [53, 82] y marino [39, 42, 81, 151], así como para celdas que contienen reflexiones fuertes de blancos [39].

La forma de la PDF Log-Weibull se ubica entre las de la PDF Weibull y Log-Normal. Las distribuciones Weibull y Log-Weibull tienden a ser más spiky con el aumento del parámetro de forma; mientras que en la Log-Normal ocurre lo contrario. La distribución log-Weibull tiene la ventaja tanto de la distribución Log-Normal como la de la Weibull. Esto quiere decir que tiene una cola larga y flexible en su forma [42].

La expresión de la PDF Log-Weibull es común para toda la literatura revisada [39, 42, 53, 82, 151]:

Donde x es la amplitud reflejada, b es el parámetro de escala y c es el de forma.

Desafortunadamente, la distribución no ha sido ampliamente aplicada en el modelado del clutter marino por múltiples autores, sino que las publicaciones relacionadas pertenecen todas a científicos asiáticos que defienden el uso de la distribución.

Distribución Tsallis.

El modelo Tsallis, pretende superar a las alternativas Weibull, Log-Normal, K y Compuesta Gaussiana en la modelación del clutter marino, proponiendo una alternativa diferencial [152-154]. Esto quiere decir que el tratamiento de los datos se realizaría en el dominio diferenciado: si se denota la amplitud del clutter marino como y(n) ,n=1,2,… los datos diferenciados del  clutter estarán definidos como [155]:

La distribución Tsallis está dada por [155]:

Donde se considera válida una variación de1 < q < 3. Nótese que cuando q = 1, se obtiene la distribución Normal. Cuando q = 2, la Tsallis se reduce a la distribución Cauchy. Además, cuando 5⁄3 < q < 3, la distribución tiene una cola que cae.

En [155] se encontró que el ajuste de la distribución Tsallis era muy bueno para clutter marino. Adicionalmente, otros trabajos dedicados a la aplicación de la distribución Tsallis al clutter marino pueden encontrarse en [156-158]. De forma general, la Tsallis parece un buen modelo, pero necesita de mayores desarrollos y validaciones para compararse con el volumen de investigaciones dedicadas a las alternativas reconocidas.

Distribución Rician Gaussiana Inversa.

En [159] fue introducida otra alternativa de modelado no-Rayleigh que emplea a la distribución Gaussiana Inversa [160-162] como componente de textura. La variante denominada distribución Rician Gaussiana Inversa (RiIG, Rician Inverse Gaussian) tiene como PDF:

Donde α, β y γ son los parámetros de la distribución, I₀ es la intensidad del ruido y γ=√(α² - β²).

La distribución ha sido empleada en estudios de comparación entre varios PDFs de amplitud [60] pero su uso no está extendido. Sin embargo, el empleo del componente Inverso Gaussiano para la textura ha sido ya probado como efectivo en otros modelos [138, 163].

Distribución Weibull-Weibull.

La distribución Weibull-Weibull es similar a la K-K en el sentido de que se compone de dos distribuciones Weibull. El principal estudio que vincula esta distribución con el clutter marino observado a ángulos rasantes elevados ocurrió en [6] donde se utilizó la siguiente PDF:

Información adicional relacionada a la distribución puede encontrarse en [72, 164, 165].

Distribución Generalizada Gamma.

La siguiente distribución da inicio al conjunto de los modelos "en transición" que el autor considera con tendencia a caer en desuso. El modelo Generalizado Gamma fue encontrado con alta similitud a los datos medidos en [81] para clutter marino de banda X. Previamente este modelo había sido empleado con gran efectividad para SAR [37, 166], siendo capaz de modelar imágenes de alta resolución con regiones heterogéneas. Su PDF es [37]:

Donde Γ(.) es la función Gamma, α es el parámetro de forma y β es el de escala. Igualmente se ha demostrado que el modelo Gamma, más sencillo que el Generalizado Gamma, es útil en la modelación de clutter spiky principalmente en la zona central de la PDF de los datos experimentales [167]. No obstante, hasta el momento, la distribución Generalizada Gamma y la Gamma han encontrado aplicación limitada para radares de apertura real, no así para SAR.

Pearson.

Un modelo que podría resultar interesante es el Pearson, que ha demostrado ser apropiado para modelar datos como señales impulsivas [168] y retornos de sonares activos [169]; en adición al clutter marino [170]. La distribución Pearson es un caso especial de la distribución simétrica Alfa-Estable cuando el parámetro característico es α=1/2. Si una variable sigue la distribución Pearson, su PDF es [171]:

Aquí, γ es el parámetro de escala que refleja el nivel medio de la potencia del clutter.

Adviértase que el modelo Pearson es de un solo parámetro, cuya influencia en la escala de la distribución puede ser cancelada por los métodos CFAR tradicionales. En efecto, se probó que varios procesadores clásicos de radar mantienen la propiedad CFAR bajo clutter homogéneo distribuido Pearson en [172, 173], y varias expresiones han sido obtenidas para la relación del modelo con varios detectores en [174]. Además, en [175] se analizó el desempeño en ambientes multi-blanco y con bordes de cambio en el nivel del clutter para fondos que siguen la distribución Pearson y múltiples tipos de CFAR; así como variantes CFAR con lógica difusa descentralizada.

La distribución Pearson podría competir con modelos simples como el Rayleigh, pero dada su definición uni-paramétrica es poco probable que adquiera relevancia. No obstante, ha sido utilizado en estudios actuales gracias a su forma sencilla [176, 177].

Distribución K con textura Log-Normal.

Una variante del modelo Generalizado K existe también para Textura Log-Normal. Aunque menos conocido que el Generalizado K tradicional (de Textura Gamma), la alternativa ha sido empleada en comparaciones de PDFs teóricas [61].

La distribución parte de fundamentos sólidos como el modelo Log-Normal y el mecanismo de formulación compuesta, pero aún adolece de evidencia robusta que la respalde.

Distribución Log-Normal Tri-paramétrica.

Existe una variante de la distribución Log-Normal que la convierte en Triparamétrica mediante la inclusión de un parámetro extra de localización (γ). Esta variante fue empleada en comparaciones realizadas en [46]. Su PDF es:

Aún de limitado uso, la distribución podría mejorar el ajuste de datos muy spiky y surgir como una alternativa para los modelos Log-Normal tradicional y Log-Weibull. Desafortunadamente, la falta de evidencia sustancial que respalde el modelo hace que se planteen dudas sobre su verdadera utilidad.

2.5.- GRUPO 5: DISTRIBUCIONES POCO USADAS

El último grupo de distribuciones se denomina Distribuciones Poco Usadas y contiene modelos que han encontrado aplicación limitada o descontinuada. Los modelos que se presentan a continuación son J-Shaped (de forma J), Alfa Estable (Alpha Stable), Normal Contaminado y el Exponencial.

Distribución J-Shaped.

La distribución J-Shaped fue ajustada a datos de amplitud para Banda Ku, polarización lineal y ángulos rasantes cercanos a la incidencia vertical en [178], empleando el método de los momentos. La principal desventaja de esta investigación es que no se comparó la exactitud del ajuste alcanzado con otras distribuciones conocidas como la K o la Weibull.

Dentro de las distribuciones J-Shaped, el ajuste correspondió al caso especial conocido como Beta J-Shaped cuya PDF es:

Donde Γ(.) es la función Gamma, y γ y η son los parámetros de la distribución.

Distribución Alfa Estable.

En un recuento de las distribuciones empleadas en la modelación de clutter efectuada en [38] se menciona la variante Alfa Estable (Alpha Stable). Empero, también en [38] se señala su limitado alcance. La PDF de la distribución tiene dos propiedades importantes que pudieran hacerla útil para el modelado del clutter. La primera propiedad es la propiedad de estabilidad, la cual establece que la suma pesada (weighted) de variables aleatorias independientes distribuidas alfa estable está distribuida nuevamente alfa estable, con el mismo exponente característico α. La segunda propiedad es el teorema del límite central. A diferencia de la distribución Normal, una distribución alfa estable puede ser también asimétrica alrededor de la media.

La mejor forma de definir la PDF de la distribución Alfa Estable es mediante la integral de transformación inversa de Fourier [179]:

El exponente característico está entre 0 y 2. La variable δ es el parámetro de localización y γ es el parámetro de dispersión [18]. La distribución no ha encontrado aún amplio uso en la literatura del clutter de radar [38], más allá de su aplicación en forma reducida como distribución Pearson, a pesar de intentos de autores de atraer el interés de la comunidad sobre el modelo como un buen ajuste para clutter [180]. Adicionalmente, el desempeño de receptores óptimos y subóptimos en presencia de la distribución Alfa Estable fue examinado en [181] y en [182].

Distribución Normal Contaminada.

En [183] fueron relacionadas las distribuciones Log-Normal y Normal-Contaminada con los datos tomados por el NRL (Naval Research Laboratory, Laboratorio de Investigaciones Navales) a un ángulo rasante de 4,70 usando un radar de banda X con polarización vertical y ancho de pulso de 0,02 μs.

La distribución Normal Contaminada ha sido utilizada para la modelación del clutter debido a que las colas largas observadas no pueden ser descritas por la distribución Normal. Una distribución Normal contaminada es una distribución donde las muestras son tomadas de dos distribuciones Normales diferentes, para crear así las colas pesadas. La mayoría de las muestras son tomadas de un distribución Normal con media μ₁ y desviación estándar σ₁. Las muestras restantes son tomadas de una segunda distribución Normal con media μ₂ y desviación estándar σ₂. La relación entre las dos distribuciones es una media igual μ₁ = μ₂, y una varianza mayor para la distribución menos muestreada σ₁ ≪ σ₂. Esto produce las colas pesadas, creándose así la distribución Contaminada Normal [184].

La PDF de la distribución Normal es [80]:

Donde μ y σ² son los parámetros de localización y escala de la distribución que coinciden con la media y la varianza.

Distribución Exponencial.

Pruebas realizadas por el laboratorio Lincoln del MIT (Massachusetts Institute of Technology, Instituto de Tecnología de Massachusetts) en la década del 90 apuntaron a la distribución exponencial. La PDF exponencial de la amplitud es dada a continuación. La variable r es conocida como parámetro de rate (razón) de la distribución. La distribución exponencial ha demostrado ser un mejor ajuste para clutter windblown (soplado por el viento) que la distribución Gaussiana [185, 186].

Este modelo es aplicado a clutter marino mayoritariamente como parte de la formulación compuesta de la distribución K. Conjuntamente, el modelo Exponencial se incluye dentro de la distribución Weibull cuando el parámetro de forma es igual a 1. Por ello, evidencia de la aplicación del modelo Exponencial para datos de clutter marino y terrestre puede encontrarse en estudios que recomiendan valores del parámetro de forma cercanos a la unidad [6, 30, 61]. La distribución Exponencial fue uno de los primeros modelos considerados pero actualmente ha sido reemplazado completamente por la Weibull que es un caso más general. A pesar de ello, puede emplearse en simulaciones que busquen maximizar la simplicidad de las variables implicadas [187].

2.6.- RESUMEN DE LA CLASIFICACIÓN

Para resumir o condensar los resultados de la escala de clasificación dada anteriormente para las distribuciones estadísticas que modelan el clutter marino los autores prepararon una tabla comparativa que incluye todas las distribuciones, a excepción de aquellas del último grupo, que son muy poco utilizadas. La Tabla 1 muestra los 7 campos fundamentales que se utilizan para comparar las distribuciones. El primero de ellos, el tipo de clutter, muestra 4 variantes fundamentales de clutter para las que pueden ser usadas las distribuciones. Por ejemplo, las distribuciones Pareto, K-K, K-A y Weibull-Weibull han sido propuestas para modelar los ecos de ángulos rasantes medios y altos, y por tanto compiten sólo en esta categoría.

La Evidencia del Ajuste y la Superioridad son dos de los campos más importantes de la tabla. El primero refleja la cantidad de publicaciones que han señalado la cercanía de la distribución al modelado del clutter; mientras que la segunda indica la frecuencia con que el modelo ofrece un mejor ajuste cuando es comparado con otros. La distribución K sostiene el mayor nivel en cuanto a Superioridad porque es la que ha prevalecido más veces como distribución preferencial del clutter.

La Definición Matemática, el Tiempo de Uso y los Desarrollos Vinculados a Radar son índices que reflejan la aceptación de la distribución dentro de la comunidad de radares. Las primeras distribuciones de la lista tienen generalmente una definición matemática sencilla y han sido utilizadas por un largo tiempo, lo que ha permitido que sean validadas en diversos estudios por diferentes autores. Igualmente, los desarrollos de soluciones de radar presentados para ellas son numerosos; por tanto, al adoptar estas distribuciones se obtiene también una gran cantidad de análisis que ya han sido desarrollados sobre ellas y que facilitan la creación o evaluación de soluciones de detección.

La Relación al Fenómeno Físico es un criterio que, aunque no influye directamente en la capacidad intrínseca de la distribución para adaptarse al fondo, se señala como un factor importante porque otorga al modelo una explicación del por qué se ajusta a las muestras de clutter. Las distribuciones K y Compuesta Gaussiana, así como sus derivadas, tienen una alta relación con el fenómeno físico porque utilizan un mecanismo compuesto por dos aportes que se corresponden con los dos tipos de olas del mar: las capilares y las olas gravitatorias. Por su parte, la distribución Rayleigh tiene una relación baja porque asume que los componentes en fase y en cuadratura pertenecen a la distribución Normal, lo que hace que la distribución de la envolvente de la amplitud sea Rayleigh. Asimismo, la Weibull tiene una relación baja con el clutter porque puede verse como una generalización del modelo Rayleigh, al que se reduce en cierta configuración de sus parámetros. En cambio, otras distribuciones como la Pareto no tienen prácticamente ninguna justificación de su cercanía con los datos de clutter, y han sido relacionadas con él únicamente mediante análisis empíricos.

 

3.   –VARIABILIDAD DE LAS EXPRESIONES EN LA LITERATURA

 

Uno de los principales problemas que resuelve esta revisión es el de la variabilidad de las expresiones encontradas en la literatura concernientes a las distribuciones estadísticas. Dado el volumen de investigaciones en la rama y la aplicación de varias de las distribuciones en diversos campos de la ingeniería, los modelos que han sido utilizados en la representación del clutter han sido formulados con diversas notaciones en distintas fuentes, abarcando desde pequeñas modificaciones hasta cambios importantes en las letras designadas a cada variable. Los autores del presente documento realizaron una revisión detallada sobre las diferentes variantes disponibles y eligieron las de uso más frecuente en cada caso. Aunque, para facilitar la comprensión del artículo, el análisis no se presenta de manera completa, los autores de este artículo consideraron importante ejemplificar el problema encontrado en la literatura a través de las variaciones de la distribución Weibull que es una de las más empleadas. A continuación se desarrolla este análisis.

La versión de PDF de la distribución Weibull usada en [39, 61, 70] es:

Donde z es la amplitud, b el parámetro de escala y c el de forma. En la definición anterior, u(z) es la función paso unitario, que indica que la distribución tiene siempre valor nulo para las cifras no positivas en el eje de las abscisas. La misma versión es usada en [37, 42, 53, 60], con la única diferencia de denotar la amplitud como x. Conjuntamente, en [32] se denotó a x como la amplitud pero fueron asignadas a los parámetros de forma y escala las letras respectivas de p y q; y en [14, 38] se usaron en su lugar k y λ.

Otra definición semejante a (2) es usada en [47]:

En este caso ocurre un cambio de notación en las variables. Ahora a representa la amplitud, γ es el parámetro de forma y w es el de escala. También se prescindió de la función de paso unitario en la definición, lo que no conlleva a ningún cambio significativo.

La expresión utilizada en [72] es igualmente equivalente a (29), aunque a primera vista parezca diferente:

En este caso x es la amplitud, α el parámetro de escala y β el de forma. Nótese que hay dos elementos que pueden llevar a confusión entre las ecuaciones de (30) y (28). Primeramente, la expresión a la izquierda de la exponencial parece diferente, pero en realidad no lo es. Las dos expresiones son iguales (exceptuando el cambio de notación) si la b fuera del denominador en (2) pasa hacia adentro. Con esa transformación quedaría c aislada, z^c-1 y b^c en el denominador. El segundo problema está en la propia notación. Para (2) b es el parámetro de escala y para (4) β es el de forma: b y β son la misma letra en abecedarios diferentes. La misma variante de (4) fue empleada en [31] con la única salvedad de considerar a E como la amplitud y en [7] donde la amplitud fue tomada como z.

Otra versión que añade más confusión a la notación es la empleada en [28], donde b es ahora el parámetro de forma:

Aquí se señala además que a = 1⁄b es un parámetro de pendiente y se presenta el parámetro 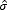₀ cuyo equivalente inverso se denota como c = 1/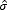₀. Adviértase que hay contradicciones de notación con respecto a (28) y (30) pero las expresiones son equivalentes si en (31) se hace  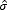₀ = b^c para (28) o  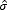₀ = α^β para (30).

Otra versión bastante difundida [6, 30] es:

Se explica en [30] que a = 1⁄b y c son referidos como los parámetros de forma y escala respectivamente. En realidad tiene más sentido elegir como parámetro de forma a b; así b en (32) es equivalente a β en (30) y a c en (28). El parámetro de escala c en (32) es igual a α^β en (30) y a b^c en (28).

Una ecuación similar a (32) se usó en [46] con un cambio de notación:

Donde α_W y β_W son, respectivamente, los parámetros de forma y escala del modelo; y a denota la amplitud [46].

Por último, en [188] se ajustaron los datos de clutter para valores de intensidad en lugar de amplitud. Se utilizó la siguiente fórmula:

Donde I es la intensidad, a es el parámetro de forma y σ² es el de escala. Como la distribución Weibull se ajusta a los datos de clutter por un mecanismo puramente empírico, el modelo de la intensidad coincide con el de la amplitud a diferencia de lo que ocurre con la distribución K. La ecuación (34) es muy parecida a la (31). El α de (34) es el b de (31), y el 2σ² de (34) es el 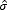₀ de (31).

A modo de conclusión, las expresiones más usadas para la PDF Weibull son la (28) y la (30) que son fácilmente transformables entre sí. El autor recomienda el empleo de la expresión (35) para eliminar la confusión existente entre las variables a, b y c que son designadas en diversas publicaciones como parámetros de forma o escala indistintamente. La expresión recomendada para el uso con Weibull queda entonces como:

La expresión (35) coincide con la (4) dada en la sección 2.

 

4.   –EXPRESIONES COMPLEMENTARIAS

 

Para  la  caracterización  completa  de  varias de las distribuciones propuestas en la revisión es necesario de un estudio particular. No obstante, los autores presentan en la Tabla 2 expresiones complementarias que pueden ayudar en la modelación del clutter marino utilizando las cinco primeras distribuciones de la lista. La notación "A/B" usada para los títulos de la Tabla 2 significa que el elemento A es dado primero y abajo se ofrece el B; por ejemplo, en el campo "CDF/Generación" se da la distribución acumulativa primero y más abajo el método de generación de variables aleatorias.

En la Tabla 2, Γ(.) es la función gamma, Kv es la función de Bessel de segunda especie y orden v, m₂ y m₄ son los momentos algebraicos de segundo y cuarto orden, E[xⁿ] es el momento algebraico de orden n, u es una variable distribuida uniformemente entre 0 y 1, E[X²] es el segundo momento algebraico, E²[X] es el cuadrado de la media, erf(.) es la función de error, erf^-1(.) es la función de error inversa, E[x] es la media y V[x] la varianza, y x_j es la muestra número j de un conjunto de n muestras.

 

5.   –VALORACIÓN DE LA INVESTIGACIÓN

 

La presente investigación reunió y clasificó 23 distribuciones estadísticas que han sido usadas por múltiples autores para modelar clutter marino y terrestre en distintas situaciones. Los modelos fueron divididos en 5 grupos atendiendo a su frecuencia de uso y resultados comprobados en la modelacion del clutter, siendo el último grupo quien incluyó las distribuciones en desuso.

El documento reune además una gran cantidad de referencias a disímiles investigaciones que brinda al lector un camino claro por el cual seguir investigando en cada distribución. La revisión realizada ofrece una notación unificada para las distribuciones, seleccionando las expresiones más comunes de entre las diferentes  variantes  utilizadas por los autores en la literatura. Por tanto, se recomienda utilizar este artículo como una guía para futuras notaciones de las investigaciones y emplear las 15 primeras distribuciones en los nuevos ajustes de datos de clutter marino y terrestre. Precisamente, la principal dificultad que se encontró en los estudios es que la mayor parte sólo utilizan un grupo muy reducido de distribuciones.

La clasificación presentada para los modelos de clutter marino dicta la dirección que ha seguido y pretende continuar el Grupo de Investigación de Radares de la CUJAE. Los modelos K, Weibull, Log-Normal, Rayleigh y Pareto (primeros en la lista) ya han sido modelados completamente en MATLAB [189, 191, 192]  y soluciones de detección adaptadas a estos modelos también han sido presentadas [193-197]. Estos resultados pretenden sintetizarse en la librería MATE-CFAR 2 (MAtlab Test Environment- for CFAR detectors, Ambiente de Prueba en MATLAB para detectores CFAR) que a su vez es una progresión del ambiente de simulación MATE-CFAR presentado en [29]. A continuación, el Grupo se enfocará en la modelación de las distribuciones Compuesta Gaussiana, K-K y K más ruido térmico, así como en la representación de las propiedades de correlación del clutter.

 

6.   –CONCLUSIONES Y RECOMENDACIONES

 

La revisión realizada muestra, por primera vez en un solo documento, la existencia de 23 distribuciones estadísticas que pueden ser utilizadas para la modelación del clutter marino. Tras ordenar y clasificar las distribuciones de acuerdo a su nivel de aplicación, se identifica que hay 15 para las cuales se ha encontrado evidencia importante que valida su uso. Sin embargo, no existen comparaciones aplicadas a estas 15 distribuciones ni a una parte significativa de ellas, por lo que este es definitivamente uno de los problemas a resolver.

Las distribuciones K, Weibull y Log-Normal, son aún las más utilizadas en la modelación del clutter marino, a pesar de que su uso fue propuesto hace ya varios años. No obstante, recientemente se han presentado alternativas interesantes, como la Log-Weibull y la Rician Gaussiana Inversa, que aún carecen de la validación suficiente para confirmar su efectividad. Una excepción lo constituye la distribución de Pareto que, a pesar de su reciente vinculación a radar, está siendo muy utilizada en la representación del clutter observado a ángulos rasantes medios y altos.

En general, las distribuciones bi-paramétricas, como la Weibull, Log-Normal, K y Pareto, son las más utilizadas en la modelación del clutter. En cambio, otras variantes, como la K más ruido, la Generalizada Gamma o la Weibul-Weibull, agregan parámetros que aumentan las posibilidades de adaptación del modelo. La adición de parámetros hace a su vez más intrincado el trabajo matemático con las distribuciones, dificultando la definición de expresiones cerradas para la función de densidad, lo que complejiza los análisis.

Uno de los elementos importantes de la revisión presentada es que recopila las notaciones empleadas con mayor frecuencia para cada una de las distribuciones. El desarrollo progresivo de los estudios sobre el clutter de radar, y el hecho de que algunas distribuciones provienen de otros campos, hace que las notaciones varíen de un autor a otro, entorpeciéndose así el entendimiento de los materiales. Para corregir este problema, se recomienda el uso de las notaciones presentadas en futuros proyectos de investigación.

Por último, se identifica que no existe una herramienta informática que proporcione un acceso fácil a la manipulación de las distribuciones y a la ejecución de análisis sobre datos de clutter. De hecho, esta es una de las limitantes para que los diferentes autores puedan conducir experimentos con un amplio conjunto de modelos. El grupo de radares de la CUJAE trabaja en este sentido, con el objetivo de crear el producto informático MATE-CFAR 2 que incluirá varias distribuciones de las citadas en el presente trabajo, así como múltiples alternativas de detección de radar. De hecho, la revisión constituye una especie de mapa que indica las distribuciones más importantes a incluir en el producto informático.

 

REFERENCIAS

 

1.             Madisetti VK. The Digital Signal Processing Handbook. 2nd ed: CRC Press; 2010.

2.             Kouemou G. Radar Technology: I-Tech; 2009.

3.             Richards MA, Scheer JA, Holm WA. Principles of Modern Radar. Vol I Basic Principles: Scitech Publishing; 2010.

4.             Skolnik MI. Radar Handbook. 3er ed: McGraw-Hill; 2008.

5.             Meikle H. Modern Radar Systems. 2nd ed: Artech House; 2008.

6.             Dong Y. Distribution of X-Band High Resolution and High Grazing Angle Sea Clutter, Technical Report DSTO-RR-0316. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organization, 2006.

7.             Ward K, Tough R, Watts S. Sea Clutter. Scattering, the K distribution and Radar Performance. 2nd ed. London, United Kingdom: The Institution of Engineering and Technology; 2013.

8.             Ward KD, Baker CJ, Watts S. Maritime surveillance radar Part 1: Radar Scattering from the ocean surface. IEE Proceedings on Radar and Signal Processing. 1990;137(2):51-62.

9.             Conte E, De Maio A, Galdi C. Statistical Analysis of Real Clutter at Different Range Resolutions. IEEE Transactions on Aerospace and Electronic Systems. 2004;40(3):903-18.

10.           Chan HC, editor. Radar Sea Clutter at Low Grazing Angles. IEE Proceedings on Radar and Signal Processing; 1990 Apr.

11.           Farina A, Russo A, Studer R. Coherent Radar Detection in Log-Normal Clutter. IEE Proceedings on Communications, Radar and Signal Processing. 1986;133(1):39-54.

12.           Jakeman E, Pusey PN. A Model for Non-Rayleigh Sea Echo. IEEE Transactions on Antennas and Propagation. 1976;24(6):806-14.

13.           Nohara TJ, Haykin S, editors. Canadian East Coast Radar Trials and the K-Distribution. IEE Proceedings on Radar and Signal Processing; 1991 Apr.

14.           Sekine M, Mao Y. Weibull Radar Clutter. New York: Peregrinus; 1990.

15.           Weinberg GV. Neyman-Pearson Optimal and Suboptimal Detection for Signals in General Clutter Mixture Distributions, Technical Report DSTO–RR–0363. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation (DSTO), 2011

16.           Watts S. Radar Detection Prediction in K-distributed Sea Clutter and Thermal Noise. IEEE Transactions on Aerospace and Electronic Systems. 1987;23(1):40-5.

17.           Anastassopoulos V, Lampropoulos GA. High Resolution Radar Clutter Classification.  IEEE International Radar Conference; Washington, D.C., USA; 1995. p. 662-7.

18.           Billingsley JB, Larrabee JF. Multifrequency Measurements of Radar Ground Clutter at 42 sites (Technical report 916, DTIC AD-A246710). Massachusetts Institute of Technology, Lincoln Laboratory, 1991.

19.           Boothe R. The Weibull Distribution Applied to the Ground Clutter Backscatter Coefficient (Technical Report RE-TR-69-15). Army Missile Command Redstone Arsenal AL Research and Engineering Directorate, 1969.

20.           Chen KS, Fung AK, editors. Frequency Dependence of Backscattered Signals from Forest Components. IEE Proceedings on Radar, Sonar and Navigation; 1995.

21.           Jao JK. Amplitude Distribution of Composite Terrain Radar Clutter and the K-Distribution. IEEE Transaction on Antennas Propagation, AP-32. 1984:1049-62.

22.           Rajalakshmi Menon K, Balakrishnan N, Janakiraman M, Ramchand K. Characterization of Fluctuation Statistics of Radar Clutter for Indian Terrain. IEEE Transactions on Geoscience and Remote Sensing. 1995;33(2):317 - 24.

23.           Chan HC. Analysis of the North Truro Sea Clutter Data (N. DREO 1051) Defense Research Establishment Ottawa (Ontario), 1990.

24.           Schleher DC. Radar Detection in Weibull Clutter. IEEE Transactions on Aerospace Electronic Systems. 1976;12:736-43.

25.           Antipov I. Simulation of Sea Clutter Returns, DSTO-TR-0647. Edinburgh, South Australia: Surveillance Systems Division, Electronics and Surveillance Research Laboratory, 1998.

26.           Raghavan RS. A Method for Estimating Parameters of K-Distributed Clutter. IEEE Transactions on Aerospace and Electronic Systems. 1991;27(2):238-46.

27.           Watts S, editor. Radar Detection Prediction in Sea Clutter using the Coumpound K-Distribution Model. IEE Proceedings in Communications, Radar and Signal Processing; 1985.

28.           Machado Fernández JR, Bueno González A. Clasificación del Clutter Marino utilizando Redes Neuronales Artificiales. La Habana (Cuba): Instituto Superior Politécnico José Antonio Echeverría; 2012.

29.           Machado Fernández JR, Bacallao Vidal JC. MATE-CFAR: Ambiente de Pruebas para Detectores CFAR en MATLAB. Telem@tica. 2014;13(3):86-98.

30.           Dong Y. Clutter Spatial Distribution and New Approaches of Parameter Estimation for Weibull and K-Distributions, DSTO-RR-0274. DSTO Systems Sciences Laboratory, Edingburgh, South Asutralia: 2004.

31.           Chen Z, Liu X, Wu Z, Wang X, editors. The Analysis of Sea Clutter Statistics Characteristics Based on the Observed Sea Clutter of Ku-Band Radar. IEEE Proceedings of the International Symposium on Antennas & Propagation; 2013 Oct.

32.           Ding HF, Guo L-X, Mao Y. Modeling Statistics of Sea Clutter from 1-D Time-Varying Sea Surface. IEEE International Conference on Microwave Technology & Computational Electromagnetics; May 2011.

33.           Ping Q, editor. Analysis of Ocean Clutter for Wide-Band Radar Based on Real Data. Proceedings of the 2011 International Conference on Innovative Computing and Cloud Computing; 2011; Wuhan, China.

34.           Palama R, Maria G, Stinco P, Gini F, editors. Statistical Analysis of Netrad High Resolution Sea Clutter. Proceedings of the 21st European Signal Processing Conference  (EUSIPCO); 2013.

35.           Shang X, Song H. Radar Detection Based on Compound-Gaussian Model with Inverse Gamma Texture. IET Radar, Sonar and Navigation. 2010;5(3):315-21.

36.           Carretero Moya J, Gismero Menoyo J, Asensio López A, Blanco del Campo Á. Experimental Validation of the Compound Gaussian Sea Clutter Model at Sub-Meter Range Resolution.  2009 International Radar Conference "Surveillance for Safer World (Radar 2009); Oct 2009.

37.           Weiping N, Weidong Y, Hui B, Junzheng W, Gang Z. Statistical Analysis of High Resolution TerraSAR-X Images for Ground Targets Detection.  2013 7th International Conference on Image and Graphics; Qingdao, China; 26-28 Jul. 2013. p. 343-7.

38.           Jurgens Strydom J. Generic Ground Clutter Simulation for Radar Testing and Evaluation: University of Cape Town; 2012.

39.           Ishii S, Sayama S, Mizutani K. Effect of Changes in Sea-Surface State on Statistical Characteristics of Sea Clutter with X-band Radar. Wireless Engineering and Technology. 2011;2(3):175-83.

40.           Watts S, Rosenberg L. A Review of High Grazing Angle Sea Clutter.  IEEE 2013 International Conference on Radar; 2013. p. 240-5.

41.           Farina A, Gini F, Greco MV, Verrazzani L. High Resolution Sea Clutter Data: Statistical Analysis of Recorded Live Data. IEE Proceedings on Radar, Sonar and Navigation. 1997;144(3):121-30.

42.           Sayama S, Ishii S. Suppression of Log-Normal Distributed Weather Clutter Observed by an S-Band Radar. Wireless Engineering and Technology 2013;4 (3):125-33.

43.           Watts S. Radar Sea Clutter: Recent Progress and Future Challenges.  IEEE 2008 International Conference on Radar; 2008.

44.           Zhang L, Li J, editors. Airship Radar System Modeling and Simulation. Progress in Electromagnetics Research Symposium Proceedings; 2012; Moscow, Rusia.

45.           Farina A, Gini F, Greco MV, Verrazzani L. Analysis of Sea Clutter Radar Data.  CIE International Conference of Radar; Beijing, China; 1996.

46.           Yim JZ, Chou C-R, Wong W-K. A Study of the Statistics of Sea Clutter in the Northern Coast of Taiwan.  Proceedings of the 17th International Offshore and Polar Engineering Conference; Lisbon, Portugal; 2007. p. 1-6.

47.           Antipov I. Statistical Analysis of Northern Australian Coastline Sea Clutter Data. Edinburgh, South Australia: Surveillance Systems Division, Electronics and Surveillance Research Laboratory, 2001.

48.           Watts S, Baker CJ, Ward KD. Maritime surveillance radar Part 2: Detection performance prediction in sea clutter. IEE Proceedings on Radar and Signal Processing. 1990;137(2):63-72.

49.           Ward KD. Compound Representation of High Resolution Sea Clutter. Electronic Letters. 1981;17(16):561-3.

50.           Jakeman E, Pusey PN. Statistics of Non-Rayleigh Microwave Sea Echo.  IEE 1977 Radar International Conference Publications; 1977. p. 105-9.

51.           Yueh SH, Kong JA, Jao JK, Shin RT, Novak LM. K-Distribution and Polarimetric Terrain Radar Clutter. Journal of Electromagnetic Waves and Applications. 1989;3(8):747-68.

52.           Oliver C, Quegan S. Understanding Synthetic Aperture Radar Images. Dedham, MA: Artech House; 1998.

53.           Sayama S, Sekine M. Weibull, Log-Weibull and K-Distributed Ground Clutter Modelling Analyzed by AIC. IEEE Transactions on Aerospace and Electronic Systems. 2001;37(3):1108-13.

54.           Haykin S, Bakker R, Currie BW. Uncovering nonlinear dynamics—The case study of sea clutter. Proceedings IEEE. 2002;90:860–81.

55.           Meng X, Feng G, Xue H, He Z. Wideband Radar Target Detection Theory in Coherent K Distributed Clutter. Research Journal of Applied Sciences, Engineering and Technology. 2013;5(5):1528-32.

56.           Tanriverdi G. Arma Model Based Clutter Estimation and its Effect on Clutter Supression Algorithms: The graduate School of Natural and Applied Sciences; 2012.

57.           Zhijian Z, Ruilai X, Yong H, Jian G, editors. New Nonparametric Detectors under K-Distributed Sea Clutter in Radar Applications. IEEE 2011 CIE International Conference on Radar; 2011.

58.           Yunlong L, Chao X, Hongzhong Z, Qiang F, editors. Modeling and Simulation of Correlated K-Dist based on ZMNL. 3er International Conference on Signal Processing Systems (ICSPS 2011); 2012; Singapur.

59.           Zhou Y, Wang X. K-Dist Clutter Generation of Airborne Phased Array Radar. Proceedings of the IEEE. 2009.

60.           Mezache A, Soltani F, Sahed M, Chalabi I. A Model for Non Rayleigh Sea Clutter Amplitudes using Compound Inverse Gaussian.  IEEE Radar Conference (RadarCon13); 29 Apr -3 May 2013.

61.           Greco M, Bordoni F, Gini F. X-Band Sea-Clutter nonstationarity: Influence of Long Waves. IEEE Journal of Oceanic Engineering. 2004;29(2):269-83.

62.           Watts S, Ward KD, editors. Spatial Correlation in K-Distributed Sea Clutter. IEE Proceedings in Communications, Radar and Signal Processing; 1987.

63.           Ward KD, Tough RJA, Shepherd PW. Modelling sea clutter: correlation, resolution and non-Gaussian statistics.  The International Radar '97 Conference Publications; 1997. p. 95-9.

64.           Schoenecker S, Willett P, Bar Shalom Y. The Effect of K-Distributed Clutter on Trackability. IEEE Transactions on Signal Processing. 2016;64(2):475-84.

65.           Jiang H, Yi W, Cui G, Kong L, Yang X. Tracking Targets in K Clutter via Particle Filter. IEEE '15 Radar Conference; 2015. p. 350-5.

66.           Preston JR, Abraham DA. Statistical Analysis of Multistatic Echoes From a Shipwreck in the Malta Plateau. IEEE Journal of Oceanic Engineering. 2015;40(3):643-56.

67.           Rosenberg L, Angelliaume S, Fiche A. Comparison of Distributions for Real and Synthetic Aperture Sea-Clutter.  IEEE 15' Radar Conference; 2015. p. 115-20.

68.           Wang Y, Zha Y, Huang Y, Zhang Y, Yang J. A Deconvolution Method for Ship Detection in Sea Clutter Environment.  IGARSS '15; 2015. p. 1590-3.

69.           Cetin A. CFAR Detection in K-Distributed Sea Clutter: The Graduate School of Natural and Applied Sciences of Middle East Technical University; 2008.

70.           Billingsley JB, Farina A, Gini F, Greco MV, Verrazzani L. Statistical Analyses of Measured Radar Ground Clutter Data. IEEE Transactions on Aerospace and Electronic Systems. 1999;35(2):579-93.

71.           Vicen Bueno R, Rosa Zurera M, Jarabo Amores MP, de la Mata Moya D. Coherent Detection of Swerling 0 Targets in Sea-Ice Weibull-Distributed Clutter Using Neural Networks. IEEE Transactions on Instrumentation and Measurement. 2010;59(12):3139 - 51.

72.           O'Connor AN. Probability Distributions Used in Reliability Engineering: University of Maryland; 2011.

73.           Haykin S, Bakker R, Currie BW. Uncovering Nonlinear Dynamics—The Case Study of Sea Clutter. Proceedings of the IEEE. 2002;90(5):860–81.

74.           Machado Fernández JR, García Delgado B, Machado Gil A. Reconocimientos de Parámetros de la Distribución K Asociados a Mediciones de Clutter Marino usando Redes Neuronales Artificiales.  VIII Congreso Internacional de Telemática y Telecomunicaciones, Convención Científica de Ingeniería y Arquitectura '14; La Habana, Cuba; 2014.

75.           Abraham DA, Lyons AP. Reliable Methods for Estimating the K-Distribution Shape Parameter. IEEE Journal of Oceanic Engineering. 2010;25(2):1-15.

76.           Owen A. Non-Uniform Random Variables: Wiley; 2013.

77.           Oliver CJ. Optimum Texture Estimators for SAR Clutter. Journal of Physics D: Applied Physics. 1993;26(11):1824-35.

78.           Vicen Bueno R, Jarabo Amores MP, Rosa Zurera M, Mata Moya D, Gil Pita R. Robustness with respect to the signal-to-noise ratio of MLP-Based Detectors in Weibull clutter. 15th European Signal Processing Conference. 2007.

79.           Vicen Bueno R, Rosa Zurera M, Jarabo Amores MP, Gil Pita R. Automatic target detection in simulated ground clutter (Weibull distributed) by multilayer perceptrons in a low-resolution coherent radar. IET Radar, Sonar and Navigation. 2010;4(2):315–28.

80.           Krishnamoorthy K. Handbook of statistical distributions with applications. 2016.

81.           Sayama S, Ishii S. Amplitude Statistics of Sea Clutter by MDL Principle. IEEJ Transactions Fundamentals and Materials. 2011;132(10):886-92.

82.           Sayama S, Ishii S. Amplitude Statistics of Ground Clutter from Town and Hill Observed by S-band Radar. IEEJ Transactions Fundamentals and Materials. 2011;131(11):916-23.

83.           Stehwien W. Statistical and Correlation Properties of High Resolution X-band Sea Clutter. IEEE Procedings. 1994:46-51.

84.           Conte E, Longo M, Lops M. Modelling and simulation of non-Rayleigh radar clutter. IEE Proceedings-F. 1991;138(2).

85.           Lin F, Qiu RC, Browing JP, Wicks MC. Target Detection with Function of Covariance Matrices under Clutter Environment.  IET International Conference on Radar Systems; 2012. p. 1-6.

86.           Melvin WL, Scheer JA. Principles of Modern Radar, Vol III Radar Applications: Scitech Publishing; 2014.

87.           Xu Y, Hou C, Yan S, Li J. Fuzzy Statistical Normalization for Target Detection in Active Sensing Data.  2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation (IMSNA); 2013. p. 932-5.

88.           Rosenberg L. Coherent Detection with Non-Stationary High Grazing Angle X-Band Sea-Clutter.  Proceedings of the 11th European Radar Conference; 2014. p. 249-52.

89.           Evans M, Hastings N, Peacock B. Statistical Distributions. 3rd ed. New York: Wiley; 2000.

90.           Weinberg GV. An Investigation of the Pareto Distribution as a Model for High Grazing Angle Clutter, DSTO-TR-2525. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation, 2011.

91.           Weinberg GV. Coherent multilook radar detection for targets in Pareto distributed clutter. IET Electronic Letters. 2011;47:822-4.

92.           Sangston KJ, Gini F, Greco MS. New Results on Coherent Radar Target Detection in Heavy-Tailed Compound Gaussian Clutter.  IEEE Radar Conference 20102010.

93.           Balleri A, Nehorai A, Wang J. Maximum likelihood estimation for compound-Gaussian clutter with inverse gamma texture. IEEE Trans Aerosp Electron Syst. 2007;43(2):775–9.

94.           Farshchian M, Posner FL, editors. The Pareto Distribution for Low Grazing Angle and High Resolution X-Band Sea Clutter. IEEE Radar Conference Proceedings; 2010.

95.           Weinberg GV. Assessing the Pareto Fit to High Resolution High Grazing Angle Sea Clutter. IET Electronics Letters. 2011;47:516-7.

96.           Weinberg GV. Coherent Multilook Radar Detection for Targets in KK Distributed Clutter: InTech; 2012.

97.           Weinberg GV. Suboptimal Coherent Radar Detection in a KK Distributed Clutter Environment. ISRN Signal Processing. 2012;2012.

98.           Weinberg GV. Coherent Multilook Radar Detection for Targets in Pareto Distributed Clutter, Technical Report DSTO-TR-2646. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation, 2012.

99.           Sangston KJ, Gini F, Greco MS. Coherent Radar Target Detection in Heavy-Tailed Compound Gaussian Clutter. IEEE Transactions on Aerospace and Electronic Systems. 2012;48:64-77.

100.         Weinberg GV. Assessing Detector Performance, with Application to Pareto Coherent Multilook Radar Detection. IET Radar, Sonar and Navigation. 2013;7:401-12.

101.         Weinberg GV. Coherent CFAR Detection in Compound Gaussian Clutter with Inverse Gamma Texture. European Association for Signal Processing (EURASIP) Journal on Advances in Signal Processing. 2013;1:1-13.

102.         Weinberg GV. Analysis of Classical Incoherent Integrator Radar Detectors in Compound Gaussian Clutter. IET Electronics Letters. 2013;49:213-5.

103.         Weinberg GV. Constant False Alarm Rate Detectors for Pareto Clutter Models. IET Radar, Sonar and Navigation. 2013;7:153-63.

104.         Weinberg GV. Constant False Alarm Rate Detection in Pareto Distributed Clutter: Further Results and Optimality Issues. Contemporary Engineering Sciences. 2014;7(6):231-61.

105.         Weinberg GV, Finch D. Analysis of a Pareto Mixture Distribution for Maritime Surveillance Radar. Journal of Electrical and Computer Engineering. 2012.

106.         Rosenberg L, Bocquet S. Application of the Pareto Plus Noise Distribution to Medium Grazing Angle Sea-Clutter. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. 2015;8(1):255-61.

107.         Gandhi PP, Kassam SA. Optimality of the Cell Averaging CFAR Detector. IEEE Transactions on Information Theory. 1994;40:1226-8.

108.         Beaumont GP. Intermediate Mathematical Statistics. London: Chapman and Hall; 1980.

109.         Aban IB, Meerschaert MM, Panorska AK. Parameter estimation for the truncated pareto distribution Journal of the American Statistical Association. 2006;101(473):270–7.

110.         Asimit AV, Furman E, Vernic R. On a multivariate pareto distribution. Insurance. 2010;46(2):308–16.

111.         Rytgaard M. Estimation in the pareto distribution. ASTIN Bulletin. 1990;20(2):201–16.

112.         Chlebus E, Ohri R, editors. Estimating parameters of the pareto distribution by means of zipf's law: application to internet research. IEEE Globecom; 2005.

113.         Metcalf J, Blunt SD, Himed B. A Machine Learning Approach to Cognitive Radar Detection.  2015 IEEE Radar Conference (RadarCon); 2015. p. 1405-11.

114.         Weinberg GV. Estimation of Pareto clutter parameters using order statistics and linear regression. IET Electronics Letters 20th. 2013;49(13):845- 6.

115.         Wang J, Dogandzic A, Nehorai A, editors. Cramer-Rao bounds for compound-Gaussian clutter and target parameters. Proc 2005 IEEE Int Conf on Acoustics, Speech, and Signal Processing (ICASSP' 2005); 2005; Philadelphia, PA.

116.         Emmanuelle J, Ovarlez JP, Declercq D, Duvaut P. BORD: Bayesian optimum radar detector. Signal Processing. 2003;83(6):1151—62.

117.         Lange KL, Little RJA, Taylor JMG. Robust statistical modeling using thet distribution. Journal of the American Statistical Association. 1989;84(Dec.):881-96.

118.         Dogandzic A, Nehorai A, Wang J, editors. Maximum likelihood estimation of compound-Gaussian clutter and target parameters. Proceedings of 12th Annual Workshop Adaptive Sensor, Array Processing(ASAP'04); 2004; Lexington, MA.

119.         Breloy A, Ginolhac G, Pascal F, Forster P. CFAR Property and Robustness of the Low Rank Adaptive Normalized Matched Filters Detectors in Low Rank Compound Context. IEEE 8th Sensonr Array and MultiChannel Signal Processing Workshop. 2014:301-4.

120.         Farina A, Gini F, Greco MV, Sangston KJ, editors. Optimum and Sub-Optimum Coherent Radar Detection in Compound Gaussian Clutter: a Data-Dependent Threshold Interpretation. IEEE National Radar Conference; 1996; Ann Arbor, Michigan, USA.

121.         Gini F. Performance Analysis of Two Structured Covariance Matrix Estimators in Compound-Gaussian Clutter. Signal Processing. 2000;80:365-71.

122.         Gini F, Farina A, Montanari M. Vector subspace detection in compound-Gaussian clutter, Part II: performance analysis. IEEE Transactions on Aerospace and Electronic Systems. 2002;38:1312-23.

123.         Yao K, Bhargava VK. Spherically invariant random processes: Theory and applications. In: Dordrecht T, editor. Communications, Information and Network Security. The Netherlands: Kluwer Academic Publishers; 2002. p. 315—32.

124.         Gini F, Greco MV, Diani M, Verrazzani L. Performance analysis of two adaptive radar detectors against non-Gaussian real sea clutter data. IEEE Transactions on Aerospace and Electronic Systems. 2000;36(Oct. ):1429—39.

125.         Akcakaya M, Hurtado M, Nehorai A, editors. MIMO radar detection of targets in compound-Gaussian clutter. Proc 42nd Asilomar Conf on Signals, Systems, and Computers; 2008.

126.         Michels JH, Himed B, Rangaswamy M. Performance of STAP tests in Gaussian and compound-Gaussian clutter. Digit Signal Process. 2000;10(4):309 –24.

127.         Sangston KJ, Gini F, Greco M, Farina A. Structures for radar detection in compound Gaussian clutter. IEEE Trans Aerosp Electron Syst. 1999;35(2):445–58.

128.         Gini F, Farina A. Vector subspace detection in compound-Gaussian clutter. Part I: Survey and new results. IEEE Transactions on Aerospace and Electronic Systems. 2002;38:1295–311.

129.         Zhang B, Luo F, Zhang L, Liu G. A New Covariance Matrix Estimation Method in Compound Gaussian Sea Clutter. Journal of Computational Information Systems. 2012;8(22):9353-9.

130.         Raj R, Bovik AC. The Multilinear Compound Gaussian Distribution.  IEEE 2012 International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2012.

131.         Dong Y. High grazing angle and high resolution sea clutter: Correlation and polarisation analyses, DSTO-RR-1972, DSTO Australia. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation, 2007.

132.         Crisp DJ, Kyprianou R, Rosenberg L, Stacy NJS. Modelling X-band sea clutter at moderate grazing angles.  International Radar Conference Radar 2008; Adelaide; 2008. p. 596–601.

133.         Rosenberg L, Crisp DJ, Stacy NJ. Statistical Models for Medium Grazing Angle X-band Sea-Clutter.  Defence Applications of Signal Processing Conference; 2009.

134.         Crisp DJ, Rosenberg L, Stacy NJ. Modelling X-band Sea-Clutter with the K distribution: Shape Parameter Variation.  Radar International Conference "Surveillance for a Safer World; 2009. p. 1-6.

135.         Rosenberg L. Persistent Sea-spike Detection in Medium Grazing Angle X-band Sea-clutter.  European SAR conference; 2012. p. 203-6.

136.         Rosenberg L, Crisp DJ. X-band Performance with Medium Grazing Angle Sea-Clutter.  European SAR Conference; 2010. p. 669-72.

137.         Rosenberg L. The effect of temporal correlation with K and KK distributed Sea-Clutter.  IEEE Radarcon Conference; 2012.

138.         Mezache A, Sahed M, Laroussi T, Chicouche D. Two novel methods for estimating the compound K clutter parameters in presence of thermal noise. IET Radar Sonar Navig. 2011;5(9):934-42.

139.         Fioranelli F, Ritchie M, Griffiths H, Inggs M, Sandenbergh S. Analysis of polarimetric bistatic sea clutter using the NetRAD radar system. IET Radar, Sonar and Navigation. 2016.

140.         Palama R, Greco MS, Stinco P, Gini F. Statistical Analysis of Bistatic and Monostatic Sea Clutter. IEEE Transactions on Aerospace and Electronic Systems. 2015;51(4):3036-54.

141.         Ritchie MA, Griffiths HD, Watts S, Rosenberg L. Statistical Comparison of Low and High Grazing Angle Sea Clutter.  IEEE '14 International Radar Conference; 2014. p. 1-5.

142.         Farshchian M. Characterization of Sea Clutter Amplitude and Doppler Bin PDFs. Washington DC, USA: Advanced Concepts Group Radar Division, Naval Research Laboratory, 2014.

143.         Al Ashwal WA, WoodBridge K, Griffiths HD. Analysis of Bistatic Sea Clutter – Part II: Amplitude Statistics. IEEE Transactions on Aerospace and Electronic Systems. 2014;50(2):1293-303.

144.         Bithas PS, Sagias NC, Mathiopoulos PT, Karagiannidis GK, Rontogiannis AA. On the performance analysis of digital communications over Generalized-K fading channels. IEEE Commun Lett. 2006;5(10):353-5.

145.         Bithas PS, Sagias NC, Takis Mathiopoulos P. The Bivariate Generalized-K Distribution and its Application to Diversity Receivers. IEEE Transactions on Communications. 2009;57(9):2655-62.

146.         Anastassopoulos V, Lampropoulos GA, Drosopoulos A, Ray M. High Resolution Radar clutter Statistics. IEEE Transactions on Aerospace and Electronic Systems. 1999;35(1):43-60.

147.         Ollila E, Tyler DE, Koivunen V, Poor HV. Complex Elliptically Symmetric Distributions: Survey, New Results and Applications. IEEE Trans on Signal Processing. 2012;60(11):5597-625.

148.         Middleton D. New physical-statistical methods and models for clutter and reverberation: The KA-distribution and related probability structures. IEEE Journal of Oceanic Engineering. 1999;24(3): 261-84.

149.         Watts S, Ward KD, Tough RJA, editors. The physics and modelling of discrete spikes in radar sea clutter. Proceedings of International Radar conference; 2005.

150.         Ward KD, Tough RJA. Radar detection performance in sea clutter with discrete spikes.  International Radar Conference; 2002. p. 253-7.

151.         Sekine M, Musha MPS, Yomita Y, Hagisawa T, Iraby T, Kiuchi E. Log-Weibull Distributed Sea Clutter. IEE Proceedings. 1980;127(3).

152.         Tsallis C, Levy SVF, Souza AMC, Maynard R. Statistical Mechanical Foundation of the Ubiquity of Levy Distributions in Nature. Physical Review Letters. 1995;75(20):3589-93.

153.         Beck C, Lewis GS, Swinney HL. Measuring nonextensitivity parameters in a turbulent Couette-Taylor flow. Physical Review E. 2001;63(3).

154.         Gheorghiu S, van Ommen JR, Coppens MO. Power-law distribution of pressure fluctuations in multiphase flow. Physical Review E. 2003;67(4).

155.         Hu J, Tung W, Gao J. Modeling Sea Clutter as a Nonstationary and Nonextensive Random Process. IEEE Conference on Radar Issues 09. 2009.

156.         Hu J, Gao J, Lynch RS, Chen G. Multi-Scale Modeling Approach for Detecting Low Observable Targets within Sea Clutter: IEEE. 2008.

157.         Tabataba Vakily V, Vahedi M. Sea Clutter Modeling Improvement and Target Detection by Tsallis Distribution.  International Conference on Advanced Computer Control; 2008. p. 715-9.

158.         Hu J, Tung WW, Gao J. A New Way to Model Nonstationary Sea Clutter. IEEE Signal Processing Letters. 2009;16(2):129-32.

159.         Eltoft T. The Rician Inverse Gaussian Distribution: A New Model for Non-Rayleigh Signal Amplitude statistics. IEEE Transactions on Image Processing. 2005;14(11):1722-35.

160.         Michael JR, Schucany WR, Haas RW. Generating Random Variates Using Transformations with Multiple Roots. American Statistician. 1976;30(2):88-90.

161.         Schwarz W. The ex-Wald distribution as a descriptive model of response times. Behav Res Methods Instrum Comput. 2001;33(4):457-69.

162.         Folks JL, Chikara RS. The inverse Gaussian and its statistical application - a review. J Roy Stat Soc. 1978;40(3):263-89.

163.         Ollila E, Tayler E, Koivumen DE, Poor V. Compound-Gaussian Clutter Modeling with an Inverse Gaussian texture distribution. IEEE Transactions on Signal Processing Letter. 2012;19(12):876-9.

164.         Prabhakar Murthy DN, Xie M, Jiang R. Weibull Models: Wiley; 2004.

165.         Bury K. Statistical Distributions in Engineering: Cambridge University Press; 1999.

166.         Werninghaus R, editor. TerraSAR-X Mission.SAR image analysis, modeling and techniques VI. Proceedings of the International Society for Optics and Photonics (SPIE); 2004.

167.         Messina M, Greco M, Pinelli G. Statistical Characterization of High Resolution SAR Images under Different Sea State Conditions.  IEEE Gold Remote Sensing Conference; 2010.

168.         Nikias CL, Shao M. Signal processing with alpha-stable distributions and applications. New York: John Wiley and Sons; 1995.

169.         Pierce RD, editor. RCS characterisation using the alpha stable distribution. IEEE National Radar Conference; 1996.

170.         Kuruoglu EE, editor. Analytical representation for positive alpha stable densities. IEEE International Conference in Acoustice, Speech and Signal processing; 2003.

171.         Leung SW, Minett JW, Siu YM, Lee MK. A fuzzy  approach to signal integration. IEEE Transactions on Aerospace and electronic systems. 2002;38(1):346-51.

172.         Pierce RD. Application of the positive alpha stable distribution.  IEEE Signal Processing Workshop on Higher-Order Statistics; Alberta, Canada; 1997. p. 420-4.

173.         Tsakalide P, Trinci F, Nikias CL. Performance assessment of CFAR processorsin Pearson-distributed clutter. IEEE Transactions on Aerospace and electronic systems. 2000;36(4):1377-86.

174.         Hilal Abdenour M, Faouzi S. Performance analysis of some CFAR detectors in homogeneous Pearson-distributed clutter. Signal Processing. 2006;86(8):2115-22.

175.         Meziani Abednour H, Soltani F, editors. Generalised Decentralised Fuzzy CA-CFAR Detector in Pearson Distributed Clutter. IEEE 10th International Conference on Signal Processing; 2010.

176.         Cai L, Ma X, Yan S, Hao C. Some Analysis of Fuzzy CAGO/SO CFAR Detector in Non-Gaussian Background.  IEEE 2nd International Workshop on Intelligent Systems and Applications; 2010. p. 1-4.

177.         Cai L, Ma X, Hao C, Yang X. Performace Analysis of Distributed Fuzzy CA-CFAR Detector in Pearson Distributed Clutter.  6th International Conference on Fuzzy Systems and Knowledge Discovery; 2009. p. 491-5.

178.         Pistola D. A New Statistical Model of Sea Clutter from Trials in Ku Band. Divisiones Sistemi Missilistici, Rome, Italy. 1997.

179.         Shao M, Nikias CL. Signal Processing with Fractional Lower-Order Moments: Stable Processes and Their Applications. Proceedings of the IEEE. 1993;81(7):986-1010.

180.         Tsihrintzis GA, Nikias CL. Evaluation of Fractional, Lower-Order Statistics-Based Detection Algorithms on Real Radar Sea-Clutter Data. IEE Proceedings on Radar, Sonar and Navigation. 1997;144(1).

181.         Tsihrintzis GA, Nikias CL. Performance of Optimum and Suboptimum receivers in the Presence of Impulse Noise Modeled as an Alpha Stable Process. IEEE Transactions on Communications. 1995;43:904-14.

182.         Liao M, Wang C, Wang Y, Jiang L. Using SAR Images to Detect Ships from Sea Clutter. IEEE Geoscience and Remote Sensing Letters. 2008;5(2):194-8.

183.         Trunk GV, George SF. Detection of targets in Non-Gaussian Sea Clutter. IEEE Transactions. 1970;6:620-8.

184.         Simkins WL, Vannicola VC, Ryan JP. SEEK IGLOO Radar Clutter Study, Rome Air Development Center, Report No. Rept. TR-77-338 (DDC AD-A047 897). 1977.

185.         Billingsley JB, Farina A, Gini F, Greco MV, Lombardo P, editors. Impact of Experimentally Measured Doppler Spectrum of Ground clutter Cancellation on MTI and STAP. Proceedings of 1997 International Radar Conference; 1997; Edinburgh, UK.

186.         Lombardo P, Greco M, Gini F, Farina A, Billingsley JB. Impact of Clutter Spectra on Radar Performance Prediction. IEEE Transactions on Aerospace and Electronic Systems. 2001;37(3):1022-38.

187.         Zhang YR, Gao MG, Li YJ. Performance Analysis of Typical Mean-Level CFAR Detectors in the Interfering target Background. IEEE 9th Conference on Industrial Electronics and Applications. 2014:1045-8.

188.         Davidson G, Griffiths HD, Ablett S, editors. Analysis of High-Resolution Land Clutter. IEE Proceedings on Visual Image Signal Processing; 2004.

189.         Machado Fernández JR, Bacallao Vidal JC. Modelación de la Distribución K en MATLAB para Aplicaciones de Radar. Revista de Ingeniería Electrónica, Automática y Comunicaciones (RIELAC). 2016;37(2):54-66.

190.         Machado Fernández JR. Modelación de las Distribuciones Weibull y Log-Normal para Aplicaciones de Radar (aceptado para publicación). Ciencias Holguín. 2016.

191.         Machado Fernández JR. Modelación de las Distribuciones Rayleigh y Exponencial en MATLAB para Aplicaciones de Radar. Telem@tica. 2016;15(2):1-15.

192.         Machado Fernández JR. Modelación de la Distribución Gamma en MATLAB para Aplicaciones de Radar. Ciencias Holguín. 2016;22(4):1-17.

193.         Machado Fernández JR, Sánchez Rams RC. Implementación de un Detector de Promediación de Clutter (CA-CFAR) usando VHDL. Telem@tica. 2016;15(2):52-61.

194.         Machado Fernández JR, Bacallao Vidal JC. Improved Shape Parameter Estimation in K Clutter with Neural Networks and Deep Learning. International Journal of Interactive Multimedia and Artificial Intelligence. 2016;3(7):96-103.

195.         Machado Fernández JR, Bacallao Vidal JC, Chávez Ferry N. A Neural Network Approach to Weibull Distributed Sea Clutter Parameter's Estimation. Inteligencia Artificial 2015;18(56):3-13.

196.         Machado Fernández JR. Estimation of the Relation between Weibull Distributed Sea clutter and the CA-CFAR Scale Factor. Journal of Tropical Engineering. 2015;25(2):19-28.

197.         González Padilla A, Bravo Quintana B, Machado Fernández JR, Bueno González A. Clasificación del Clutter Marino utilizando Redes Neuronales Artificiales. Revista de Ingeniería Electrónica, Automática y Comunicaciones (RIELAC). 2013;34(1):1-11

 

 

Recibido: 2 de diciembre del 2016      
Aprobado: 21 de febrero del 2017

 

 

José Raúl Machado Fernández, Ing. en Telecomunicaciones y Electrónica, Profesor e Investigador, Aspirante a Doctor, Grupo de Investigación de Radares, Departamento de Telecomunicaciones y Telemática, Facultad de Telecomunicaciones y Electrónica, Universidad Tecnológica de la Habana "José Antonio Echeverría" (CUJAE), La Habana, Cuba. Correo electrónico: [e-mail]