ARTÍCULO ORIGINAL

 

 

Algoritmo de transformación de campo cercano a campo lejano en coordenadas planas

 

Alghorithm of near field transformation to far field in planes coordinates

 

Ailén Pérez Molinet, José R. Sandianes Gálvez, Leslye Villar Ledo

Departamento de Telecomunicaciones y Telemática de la Universidad Tecnológica de La Habana José Antonio Echeverría (CUJAE). La Habana, Cuba.

 

 

---

RESUMEN

Las mediciones estándar en campo lejano, para antenas de grandes dimensiones, son difíciles de realizar porque la distancia entre la antena a medir y la sonda se hace demasiado grande para enmarcarla dentro de un rango de prueba real. Sin embargo, se hace necesaria la medición en esta región porque en ella se determinan parámetros fundamentales como el patrón de radiación. Estas mediciones pueden realizarse, no obstante, en el campo cercano, lo cual proporciona un rápido y exacto método para determinar, mediante el empleo de las técnicas de transformación de Fourier, los parámetros fundamentales de una antena bajo prueba (AUT). La utilización de un "software", en este caso el MATLAB, permite la simulación del comportamiento en el campo lejano y comprobar la exactitud del modelo a medir a partir de una medición de campo cercano.

El objetivo del trabajo es implementar un algoritmo de transformación utilizando el sistema de coordenadas planas. El mismo ha sido desarrollado por el grupo de investigación de Radiopropagación, del Departamento de Telecomunicaciones y Telemática. Con esto se pretende contribuir al diseño de la cámara anecoica en la CUJAE y utilizarlo como el método para la transformación de las mediciones hechas en campo cercano dentro de la cámara a mediciones de campo lejano. El algoritmo propuesto ha sido validado, tomando como base una antena cuya característica direccional es conocida como una bocina piramidal.

Palabras claves: campo cercano, campo lejano, cámara anecoica.

---

ABSTRACT

The standard measurements of far-field antennas are difficult to implement for large antennas, since the measurement distance between the measuring antenna and the probe may become too large to place it within a range of actual test. However, it is necessary to make the measurement in this region because important parameters of antennas are determined as radiation pattern. These measurements can then be performed in the near field that provides a method for determining, through the use of processing techniques, the basic parameters of an antenna under test (AUT). The use of a software, in this case MATLAB, allows the simulation of far field behavior and prove the accuracy of the model from a near field measurement.

This work is to implement an algorithm for planar coordinate transformation. His development is linked to researching of Radiopropagation group in Telecommunications and Telematics Department. This is the researching aims to contribute to the design of the anechoic chamber in CUJAE and in the use of the method that transforms near-field results (measured inside the chamber) to far field. The work has been validated with a known radiation pattern as is from a pyramidal horn.

Key words: near field, far field, anechoic chamber.

---

 

 

1.- INTRODUCCIÓN

 

Las comunicaciones inalámbricas han venido experimentando un desarrollo creciente desde hace ya algunos años. Los sistemas de comunicaciones inalámbricas para contribuir a este desarrollo tecnológico demandan movilidad, mayor alcance, menor tamaño y menor costo en las soluciones. Por consiguiente, las antenas como dispositivo esencial en dichos sistemas, también deben cumplir con esas características.

Las antenas son los dispositivos usados para la emisión de ondas electromagnéticas en diferentes condiciones ambientales y existen una gran variedad de ellas como por ejemplo las presentadas en [1,2]. La forma en que ellas irradian la energía es considerada por la representación de los campos radiados en función de la dirección en el espacio, denominada característica direccional o patrón de radiación, el cual puede ser direccional, omnidireccional, o de otra forma [3]. Para lograr el adecuado funcionamiento de estos dispositivos electromagnéticos, se hace necesario evaluar su comportamiento a fin de perfeccionar y validar los resultados de las emisiones electromagnéticas radiadas. De este modo ha surgido la necesidad de encontrar sitios, o crear instalaciones, donde se pudiera realizar el estudio y comprobación del rendimiento y funcionamiento de las antenas u otros dispositivos que irradien energía electromagnética.

El lugar propicio para realizar la medición de uno o varios parámetros de una antena, o de un circuito de microondas, es denominado campo abierto ideal, cuyas siglas en inglés son OATS (Open Area Test Site). Este sitio, de acuerdo con la norma ANSI (American National Standars Institute) C63.4-1992, es un lugar abierto, que se caracteriza por ser de superficie plana, terreno nivelado y limpio, y debe estar libre de interferencias y obstáculos, con excepción de los que se requieren para realizar dicha medición. A pesar de que estas instalaciones son clásicas de ensayo al aire libre, -OATS son una referencia de gran precisión para un buen número de normas internacionales-, sufren un problema endémico: las interferencias externas.

Debido a la dificultad de encontrar una zona libre de interferencias e independiente de las condiciones climáticas han sido creadas, para solventar este problema, las cámaras anecoicas, las que generan con gran exactitud las condiciones de propagación en el espacio libre, evitando las interferencias. Es por esto que las cámaras anecoicas tienen una doble misión: atenuar las interferencias externas para evitar su influencia en el interior, mediante el respectivo apantallamiento, y atenuar los campos generados en el interior que pudiesen afectar la medición, mediante materiales absorbentes de las ondas electromagnéticas [4].

Las cámaras anecoicas son de tamaño finito, por lo que no siempre es posible realizar las mediciones en la zona que es considerada como campo lejano; por esa razón es necesario disponer de técnicas de transformación de los valores medidos en campo cercano a valores de campo lejano y, de este modo, obtener la caracterización completa de los parámetros del sistema radiante medido en la zona lejana.

Actualmente el grupo de investigación de Radiopropagación, perteneciente al Departamento de Telecomunicaciones y Telemática, de la Universidad Tecnológica de La Habana ¨José Antonio Echeverría¨, en conjunto con otras instituciones interesadas, están vinculados a un proyecto que consiste en la construcción de una cámara anecoica para la caracterización de antenas y objetivos de blancos de radiolocalización. Esta cámara debe alcanzar la capacidad de medir en campo cercano estos elementos radiantes, lo que ampliaría la capacidad de las prestaciones de la misma. En Cuba nunca se ha construido una cámara anecoica, por lo que la realización de este proyecto sería un evento novedoso para el país.

Sin embargo, lograr estos objetivos no se hace de una forma directa, sino que se requiere contar con algoritmos que permitan transformar los valores de campo medido en zona cercana en una transformación integral del campo que la antena desarrolla en su zona lejana. [5]

Existen diferentes trabajos enfocados a lograr la transformación que nos proponemos como objetivos, pero el hecho de no constar con mediciones nos ha llevado a la realización de construir tal algoritmo.

Uno de estos artículos citados anteriormente trata la transformación del campo a partir de redes neuronales. Las redes neuronales se proponen como una herramienta eficiente capaz de realizar transformación de campo cercano a campo lejano, directamente a través de la aplicación del Teorema de Equivalencia. Una red neuronal puede ser entrenada para relacionar los datos de campo cercano con datos de campo lejano o con una distribución de corriente equivalente y luego éste con el campo lejano del correspondiente patrón de radiación. Esto método presenta un gran coste computacional, a pesar de que solo haya que realizarlo una vez. En este artículo se proponen dos enfoques neuronales diferentes para el problema del campo cercano al campo lejano (NF-FF). El más simple se basa en el teorema de la equivalencia. [6]

En un segundo artículo se desarrolla un procedimiento eficiente para la reconstrucción de campo lejano a partir de datos que son de campo cercano en una hélice circular. La aplicación de una sonda integrada se considera para recopilar datos de amplitud que son utilizados aquí en la recuperación de fase de campo cercano. [7] Otro artículo muestra un algoritmo de interpolación de muestreo óptimo que permite la recuperación exacta de muestras plano-rectangulares de campo cercano a partir del conocimiento del plano-polar. [8]

En otro de los artículos se revisan los fundamentos teóricos de las transformaciones de campo cercano-lejano con escaneos en espiral y se proporciona una teoría unificada. Esto se logra introduciendo una representación de muestreo del campo electromagnético radiado sobre una superficie rotacional a partir del conocimiento de un número no redundante de sus muestras sobre una envoltura en espiral de la superficie. [9]

Estos artículos tratan la transformación del campo cercano a campo lejano a partir de mediciones, o sea, no la tratan de la misma forma que lo hemos empleado, pues el no contar con estas mediciones ni con una cámara anecoica para la validación, significa que las condiciones han cambiado y por tanto el algoritmo propuesto consideramos que es novedoso.

Todos los sistemas de medición de campo cercano calculan el campo en las direcciones en las que la energía electromagnética se propaga, las que son completamente independientes de la distancia a la AUT. El sistema opera midiendo, dentro del campo cercano, el frente de onda de la AUT y por medio de la transformada bidimensional de Fourier se convierte el frente de fase a un espectro angular equivalente. En el método considerado, una sonda ideal explora moviéndose sobre una superficie plana-rectangular. Es de suponer que en estas condiciones no se realizan las correcciones necesarias por los errores que durante la lectura se puedan introducir, a no ser que se consideren medidas adicionales.

En general, un sistema de medición planar está bien preparado para antenas de mediana y alta ganancia, especialmente, arreglos de antenas en fase, y requiere la menor cantidad de cálculos, además no es necesario el movimiento de la antena de prueba. Aunque el sistema cilíndrico requiere más cálculos que el caso planar, su medición es necesaria para muchas antenas. Por último, el sistema esférico es el que requiere de cálculos más engorrosos, el posicionamiento de la AUT y de la sonda son bastante complicados. Éste último método puede ser necesario para sistemas de grandes antenas, además es el más factible para las mediciones de antenas omnidireccionales de baja ganancia. Como la investigación se encuentra en una primera fase de desarrollo hemos escogido el método de coordenadas planas para desarrollar el algoritmo de transformación debido a la sencillez que el mismo presenta.

El área de muestreo plano-rectangular debe satisfacer los siguientes requisitos:

- Debe ser lo suficientemente grande para permitir que se capte toda la energía significativa de la AUT;

- Las dimensiones correctas del área pueden determinarse mediante la expresión:

donde: L es la dimensión del área de muestreo; D es la mayor longitud de la AUT; Z es la distancia entre la sonda y la AUT; y Ɵv es el ángulo crítico, o máximo posible, de la zona de muestreo.

Las posiciones discretas en las cuales la sonda medirá el campo cercano deben ser bien definidas y satisfacer el teorema de muestreo de Nyquist, lo cual permite minimizar el tiempo de adquisición de los datos y requisitos del almacenamiento. Los puntos de muestreo normalmente se colocan en una rejilla de dos dimensiones. La zona de campo cercano radiante, donde se deben realizar las mediciones, debe estar comprendida entre 3λ y 10λ, aproximadamente.

En general el campo lejano se evalúa por la siguiente expresión:

donde: r es la distancia desde la superficie de escaneo a la AUT, k es el número de onda en el espacio libre y Ȧ(k_x, k_y) es la función espectral de onda plana (PWS), la que está dada por:

donde: E(x, y, 0) es la distribución del campo eléctrico sobre la superficie de muestreo; kx, ky y kz son los números de ondas en las direcciones: x, y, z, respectivamente, las que pueden ser escritas en función de los ángulos θ y ϕ en un sistema de coordenadas esféricas:

Las integrales de la expresión (3) pueden ser reemplazadas si consideramos un conjunto discreto de n × m muestras de campo cercano, medidas sobre la superficie plana-rectangular, por lo que Ȧ(k_x, k_y) se puede escribir como:

donde: Ė_l,k(x, y, 0) son las muestras del campo Ė complejo sobre la superficie de muestreo; x_i y y_k, son las posiciones de la sonda para estas muestras. De este modo, el campo lejano, en un sistema de coordenadas esféricas, para el conjunto discreto de muestras se expresa por:

El modelo más allá de ± θv no es válido, así:

Aquí S es la longitud del área de lecturas (escaneo); D, es el diámetro de la AUT; r₀, es la distancia de separación entre la abertura de la AUT y el plano de lecturas.

 

2.- ECUACIONES GENERALES DEL CAMPO ELÉCTRICO Y MAGNÉTICO DE CUALQUIER ANTENA

 

Las expresiones siguientes muestran la determinación de los campos producidos por cualquier antena cuyas fuentes eléctricas y magnéticas sean conocidas. A partir de las expresiones originales publicadas en [10] se puede llegar a:

donde A, B y C son:

= - ', y /R es un vector unitario que indica la dirección de ; h es la impedancia de onda, 120p en el espacio libre.

Cuando las fuentes de radiación están dispuestas solo en la superficie de la antena (lo cual es muy frecuente), los vectores de densidad de corriente eléctrica 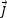_e y magnética 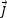_m, se expresan en (A/m) y (V/m), respectivamente, y la integral devolumen se convierte enuna integral de superficie. Se demuestra que:

Al considerar (15) sobre una superficie radiante plana, las corrientes 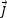_e y 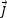_m, se convierten en las densidades superficiales de corrientes: 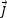_se y 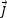_sm, las que se expresan en función de las coordenadas rectangulares de la abertura como:

donde: u_x, u_y, son los vectores unitarios sobre la superficie radiante (abertura de la antena); u_z es perpendicular a ella. Es y Hs, son los respectivos campos sobre la abertura, cuyas distribuciones dependen de las coordenadas X e Y.

Como se puede observar en las expresiones (10-15), los campos producidos por una antena cualquiera, de dimensiones comparables o mayores que la longitud de onda, tienen una estructura que depende fuertemente de la distancia R hasta el punto de observación, y son aplicables a cualquier zona de la misma incluso a la zona cercana. De este modo, mediante estas expresiones, podemos obtener los valores de campo cercano a distancias muy próximas a la abertura de la antena de prueba y simular los valores de las muestras medidas, lo que permite, mediante la transformada de Fourier, determinar el campo lejano de la antena en todas las direcciones.

En el trabajo, para la determinación, en la zona lejana, de los campos de los diferentes tipos de antenas posibles (bocinas, dipolos, arreglos de dipolos, etc.), se emplean las expresiones analíticas de los mismos, las que pueden ser encontradas en [3-4]. Los campos hallados con estas expresiones nos sirven de referencia comparativa de los campos determinados por medio de la transformación propuesta.

 

3.   -RESULTADOS Y DISCUSIÓN

 

Para la implementación de la transformación en MATLAB, fueron creadas tres funciones, las cuales tienen como variable de entrada: la frecuencia de operación durante las mediciones, definición de las dimensiones de la antena de bocina piramidal y obtención del campo.

La primera función llamada Cnear fue creada con el objetivo de evaluar las muestras de campo cercano en la superficie de muestreo definida, mediante la implementación de las ecuaciones (10) y (11), de donde se obtuvo la característica direccional en 3D de la antena como se muestra en la Figura 2.

La segunda función llamada Cfart fue creada con el fin de generar el campo lejano teórico de la antena, mediante la implementación de las expresiones de los campos de la bocina piramidal (3).

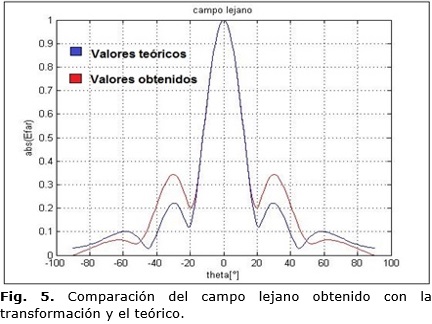
La tercera función llamada trans fue creada con el objetivo de implementar el algoritmo de transformación presentado (8) y validarlo comparando el campo lejano teórico calculado con el campo lejano obtenido. De esta función se obtuvo el espectro angular del campo lejano mostrado en la Figura 4. Se realizó la comparación entre el campo lejano teórico y el obtenido mediante el desarrollo del algoritmo de transformación, como se muestra en la Figura 5.

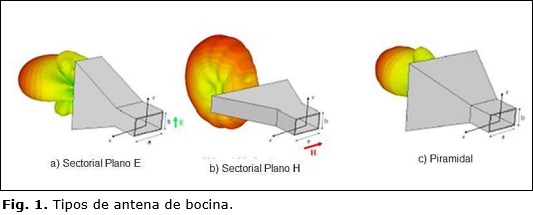
La antena de prueba consiste en una bocina piramidal (Figura 1c) con su abertura dispuesta en un plano paralelo al x-y. Las ondas se propagan en las direcciones radiales de un sistema de coordenadas esféricas (r, q, f) cuyo origen está en la abertura de la antena, la que es perpendicular al eje z. Elmodelo tiene las siguientes dimensiones:

      •   R_e= 103.803 cm

      •   R_h= 107.413 cm

      •   a_b(abertura de la bocina plano H) = 39.307 cm

      •   b_b(abertura de la bocina plano E) = 28.22 cm

      •   a(dimensión de la cara ancha de la guía de ondas)= 4.039 cm

      •   b(dimensión de la cara estrecha de la guía de ondas) = 2.019 cm

      •   L_e (longitud axial del plano E) = 93.376 cm

      •   L_h(longitud axial del plano H) = 93.376 cm

La medición fuerealizada en campo cercano en las siguientes condiciones:

      •   Distancia de la AUT a la sonda (r₀): 5.62λ

      •   Área de muestreo (A_m): 2.6λ X 2.6λ

      •   Dimensión máxima de la AUT (D): 4.35λ

      •   Frecuencia de trabajo: 3 GHz

      •   Puntos de muestreo (ΔX; ΔY) espaciados a: 0.1λ

 

4.   -IMPLEMENTACIÓN DEL PROCESO DE TRANSFORMACIÓN

 

Al implementar en MATLAB las ecuaciones de campo cercano presentadas en (10) y (11), y considerando que los vectores unitarios u_x, y u_y, se relacionan con los vectores unitarios en coordenadas esféricas: u_q, u_f y u_r [10], se obtiene la distribución de campo eléctrico en la zona cercana o de Fresnel, tal como semuestra en la Figura 2.

Posteriormente se simula el campo lejano teórico de la antena de bocina implementando las expresiones publicadas por Balanis [4] para una antena de bocina piramidal en, los que se muestran en la Figura 3.

Finalmente se presenta el algoritmo de transformación, el cual nos brinda los resultados mostrados en las Figuras 4 y 5.

Como se puede observar en la Figura 5, el valor del campo mediante la transformación es muy cercanoal valor teórico en, prácticamente, todo el lóbulo principal (± 20°). La mayor diferencia se presenta en la zona próxima al primer lóbulo secundario de la antena. Esto se debe a la alta complejidad de las expresionesutilizadas para calcular tanto el campo cercanocomo el campo lejano de la antena de bocina; esta situación ha requerido que fueran utilizados varios métodos de aproximación al realizar laimplementación en MATLAB, lo que conlleva a unnivel de errorconsiderable en esta región del diagrama direccional. Este error se manifiesta con fuerza al modificar los parámetros del sistema de medición, el paso del muestreo, etc., todo lo cual debe ser investigado más detenidamente.

 

5.   -CONCLUSIONES

 

El propósito del trabajo ha consistido en estudiar la técnica, para la transformación a campo lejano, del campo cercano obtenido por muestreo discreto sobre la superficie plana y rectangular de la antena investigada. La conversión emplea la transformada rápida de Fourier. El algoritmo, implementado en MATLAB, ha sido validado comparando los valores obtenidos con los valores del diagrama de radiación teórico de la antena. Ambos muestran una gran concordancia en el lóbulo principal; las discrepancias, en los restantes lóbulos, pueden explicarse por la falta de ajuste en los parámetros del muestreo. Esta particularidad, al igual que los errores cometidos por: dimensiones no puntuales de la antena de sondeo, sus corrimientos axiales etc., deben ser objeto de investigación posterior.

El resultado de la transformación de campo cercano a campo lejano fue empleado, también, en un arreglo lineal de N dipolos con resultados, también, satisfactorios. Se concluye que la técnica desarrollada de exploración del campo cercano, y su posterior transformación a campo lejano, es confiable para el sistema de medición considerado. Este análisis sirve de punto de partida para el análisis en otros sistemas de coordenadas (cilíndrico, esférico).

 

REFERENCIAS

 

1.       Rodríguez D, González E, Coto M, Marante FR. Antena doble banda alimentada por proximidad para aplicaciones de WLAN en 2.4 y 5.2 GHz. Revista Ingeniería Electrónica, Automática y Comunicaciones. 2014; 35(2): 11-24.

2.       Fernández FA, Rodas DA, Rodríguez D, Marante FR. Diseño de una antena Logarítmica Periódica Impresa en la banda de 470-890 MHz. Revista Ingeniería Electrónica, Automática y Comunicaciones. 2015; 36(2): 53-61.

3.     Balanis CA. Modern Antenna Handbook. 4th ed. New York: John Wiley and Sons; 2008.

4.       Balanis CA. Antenna Theory, Analysis and Design. 3rd ed. New Jersey: John Wiley and Sons; 2005.

5.       Yaghjian AD. An overview of near-field antenna measurements. IEEE Transactions on Antennas and Propagation. 1986; 34(1): 30–45.

6.       Ayestarán RG, Las-Heras F. Near field to far field transformation using neural networks and source reconstruction. Journal of Electromagnetic Waves and Applications. 2006; 20(15): 2201–2213.

7.       Constanzo S,Di Massa G. Far-field reconstruction from phase less near-field data on a cylindrical helix. Journal of Electromagnetic Waves and Applications. 2004; 18(8): 1057–1071.

8.       Bucci OM,Gennarelli C, Savarese C. Fast and accurate near-field far-field transformation by sampling interpolation of plane-polar measurements. IEEE Transactions on Antennas and Propagation. 1991; 39(1): 48–55.

9.       D'Agostino F, Gennarelli C, Riccio G. Theoretical foundations of near-field far-field transformations with spiral scanning's. Progress in Electromagnetics Research. 2006; 61(1): 193–214.

10.    Pérez Stincer EA. Antenas: Teoría General. 1st ed. La Habana: Ediciones ligeras del Instituto Técnico Militar José Martí; 2001.

 

 

Recibido: 11 de mayo del 2017
Aprobado: 23 de septiembre del 2017

 

 

Ailén Pérez Molinet, Departamento de Telecomunicaciones y Telemática de la Universidad Tecnológica de La Habana José Antonio Echeverría (CUJAE). Correo electrónico: [e-mail].