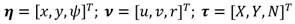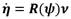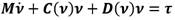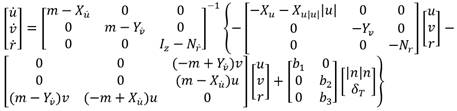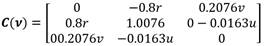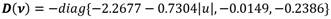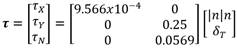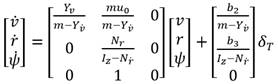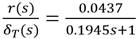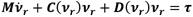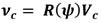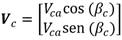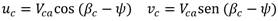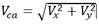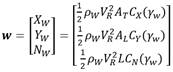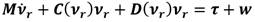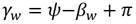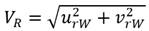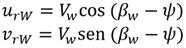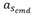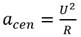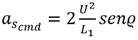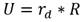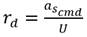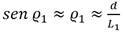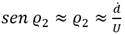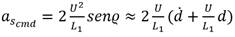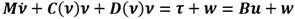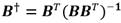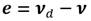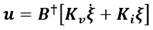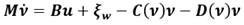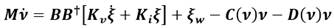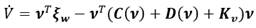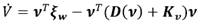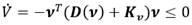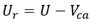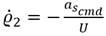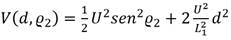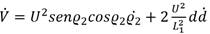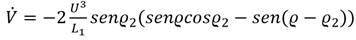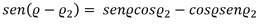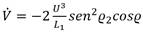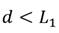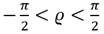Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Los vehículos autónomos de superficie (ASV) son embarcaciones marinas que tienen un alto grado de autonomía y no necesitan la acción directa de los seres humanos. Estos buques tienen un gran número de aplicaciones, principalmente en el campo de la investigación ambiental. La mayoría de las misiones que llevan a cabo estos vehículos se enmarcan en el escenario de seguimiento de caminos [1], para lo cual contar con un algoritmo o ley de guiado se hace necesario. Estos son utilizados con el objetivo reducir el error de seguimiento del camino (distancia entre la posición del vehículo y la trayectoria predefinida) y minimizar la diferencia entre el ángulo de rumbo del vehículo y el ángulo de rumbo predefinido. Otro problema que afecta el cumplimiento de las misiones, es la influencia de las perturbaciones ambientales, principalmente el viento y las corrientes marinas, por lo tanto, es importante que el algoritmo de guiado elegido pueda garantizar cero errores de seguimiento del camino a pesar de la influencia de esas perturbaciones ambientales.
Los algoritmos para el seguimiento de caminos se pueden dividir en dos categorías: algoritmos geométricos y los basados en la teoría de control [2]. Las técnicas de control son ampliamente utilizadas, principalmente las no lineales. En [3] la ley no lineal basada en un controlador PD se usa con el propósito de lograr que un vehículo subacuático siga una trayectoria de referencia en el plano horizontal. Otras técnicas son el control de modo deslizante [4] y el control inteligente [5]. Estos métodos consisten en complejos controladores multivariables difíciles de implementar en buques que operan en tiempo real. Por otro lado, los algoritmos geométricos son en su mayoría sencillos de implementar, estos se basan en colocar un punto virtual (PV) sobre el camino y utilizar este PV para hacer que el vehículo converja hacia la trayectoria deseada. La distancia entre el PV y la posición de ASV a menudo se denomina distancia virtual. Estos algoritmos incluyen la persecución pura y la línea de visión (LOS), basados estos dos en la teoría de guiado de misiles; además de la ley de guiado no lineal (NLGL) [2]. Las leyes de guiado basada en LOS por sí mismas no pueden garantizar cero error de seguimiento de camino en presencia de perturbaciones ambientales. Sin embargo, se pueden modificar agregando una acción integral para eliminar la influencia perturbadora [6, 7]. El algoritmo NLGL ha surgido en los últimos años para su uso en vehículos aéreos [8, 9]. Ha sido presentado como una interesante opción para el seguimiento de caminos por parte vehículos marinos al no utilizar el ángulo de guiñada para lograr sus objetivos de control [2, 10]. La obtención precisa de este tipo de variable ha presentado problemas durante pruebas experimentales realizadas por el GARP, debido a que los instrumentos que la miden son sensibles a campos magnéticos. En un trabajo anterior se comprueba que un esquema basado en el algoritmo NLGL es capaz de seguir caminos rectos sin error de seguimiento de caminos en presencia de corrientes marinas [11]. En este estudio, sin embargo, no se tiene en cuenta el viento como perturbación. Este trabajo se estudia cómo aplicar un esquema de guiado basado en el algoritmo NLGL para un pequeño ASV llamado Krick Felix en presencia de perturbaciones de viento lo cual no había sido tenido en cuenta previamente. Este esquema va a permitir al vehículo seguir un camino recto sin errores sin la necesidad de la medición del ángulo de guiñada y evitando la implementación de una acción integral en lazo externo, con su consecuente ventaja en la estabilidad del sistema. Tomando como base la linealización del modelo del vehículo y del algoritmo NLGL, se realizará un análisis detallado de como las perturbaciones ambientales, específicamente el viento y las corrientes marinas, afectan dicho esquema. Además, un análisis de estabilidad no lineal de Lyapunov es presentado para el caso de seguimiento de caminos rectos del esquema. Los resultados del esquema durante el seguimiento de caminos por parte del Krick Felix serán presentados mediante simulación y pruebas experimentales.
Descripción general del Krick Felix
El Krick Felix (Figura 1) es un modelo a escala de un buque del puerto de Hamburgo que está siendo utilizado por el Grupo de Automatización, Robótica y Percepción (GARP) de la Universidad Central “Marta Abreu” de Las Villas (UCLV) para el estudio de guiado y control en vehículos autónomos. El barco original fue construido en el año 1960, y ha sido usado para operaciones portuarias y de transportación.
El casco del Krick Felix está fabricado con un material conocido como Acrilonitrilo Butadieno Estireno de alta calidad, dispone de una quilla moldeada para facilitar la instalación del timón. A su vez la línea de agua marcada en el casco facilita la instalación de la cubierta. Para su movimiento la embarcación cuenta con un motor eléctrico y una propela acoplada. Algunas de las principales especificaciones de la embarcación se muestran en la Tabla 1.
Modelo dinámico del ASV Krick Felix
Durante la navegación, un vehículo marino experimenta movimientos en los 6 grados de libertad (GDL). Los grados de libertad están determinados por los desplazamientos y rotaciones independientes que especifican totalmente la posición y orientación del vehículo. En la Tabla 2 se resume la nomenclatura empleada para describir el movimiento de las embarcaciones marinas [12].
Tabla 2 Notación utilizada para vehículos marinos.
| Traslación | Fuerza | Velocidad | Posición |
|---|---|---|---|
| Avance | |||
| Desplazamiento Lateral | |||
| Arfada | |||
| Rotación | Momento | Velocidad | Angulo |
| Balanceo | |||
| Cabeceo | |||
| Guiñada |
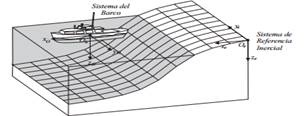
Al analizar los movimientos de las embarcaciones marinas en los 6 GDL es conveniente definir dos sistemas de coordenadas como se indica en la Figura 2. El sistema de referencia móvil es convenientemente fijado en el vehículo y es llamado Sistema del Barco. El origen de este sistema usualmente se sitúa en el Centro de Gravedad (CG), siempre y cuando pertenezca al plano principal de simetría, como es el caso del Krick Felix. Para vehículos marinos los ejes x 0 , y 0 , z 0 coinciden con los ejes principales de inercia y son usualmente definidos como: x 0 - eje longitudinal (de popa a proa), y 0 - eje transversal (de babor a estribor) y z 0 - eje normal (de arriba a abajo).
Asumiendo que los barcos son longitudinal y lateralmente metacéntricos con pequeñas amplitudes de los ángulos φ = θ = φ =θ ≈ 0, se puede descartar la dinámica de balanceo y cabeceo. La dinámica relativa al movimiento de arfada también se puede despreciar ya que el barco flota con z ≈ 0. El modelo resultante del barco en el plano horizontal se convierte entonces en un modelo de 3 GDL. Los estados para la embarcación son (ecuación 1):
(1)
donde η denota el vector de posición expresado en el marco de referencia en tierra, ν representa el vector velocidad lineal y angular con coordenadas en el sistema de la embarcación y τ representa las fuerzas y momentos que actúan sobre el vehículo en el sistema de coordenadas del mismo. Las ecuaciones cinemáticas se pueden expresar en forma vectorial utilizando las transformaciones de ángulos de Euler como (2) [13]:
(2)
donde R(ψ) es la matriz de transformación del Sistema del Barco al Sistema de Referencia Inercial, y queda definida como (3):
(3)
Por otra parte, las ecuaciones de movimiento para vehículos marinos se obtienen a partir de establecer un origen para el Sistema del Barco. De esta manera se aprovechan los beneficios que brindan las propiedades geométricas del vehículo. Al aplicar la segunda Ley de Newton se puede describir el comportamiento dinámico de la embarcación como (4) [14]:
(4)
donde
M es la matriz de inercia, C(ν) es la matriz de los términos de Coriolis, D(ν) es la matriz de amortiguamiento y τ representa el vector de fuerzas y momentos de las entradas de control. La ecuación (4) se puede escribir como [15]:
(5)Donde X u , Y v y N r son masas añadidas; X u , Y v y N r son términos de arrastre lineal; X u|u| es un término de arrastre cuadrático; y b 1 , b 2 y b 3 son coeficientes de ganancia del actuador. Las señales de entrada son: n las revoluciones del motor y δ T el ángulo de desviación del timón de popa. Para el desarrollo de los experimentos, todos los valores de los parámetros del modelo fueron obtenidos de acuerdo con la estructura geométrica del vehículo y los datos inerciales (Tabla 1). Así como un conjunto de experimentos realizados con el vehículo [11]. Los valores del modelo dinámico de 3 GDL se muestran a continuación (6), (7), (8), (9):
(6)
(7)
(8)
(9)
Modelo Dinámico Lineal
El modelo de 3 GDL presentado anteriormente se puede desacoplar en varios subsistemas, entre los cuales hay poca interacción. Esto es posible debido a las propiedades geométricas de Krick Felix. Los dos subsistemas en los que se divide el modelo 3 GDL de Krick Felix y sus variables de estado son: Subsistema lateral: estados (v, r, ψ). Subsistema de velocidad: estado (u)
En el estudio de la maniobrabilidad del ASV por modelos lineales se supone que su velocidad (u) permanece constante. Como se muestra en [11] se puede obtener un modelo lineal de 3 GDL para el subsistema lateral como se muestra a continuación (10):
(10)
De la ecuación (10) se puede obtener una función de transferencia entre el ángulo del timón de popa δ T y la velocidad angular r. Esta representación se conoce como el modelo Nomoto de primer orden [13] y se utiliza para el ajuste de los controladores. El modelo Nomoto de primer orden para el ASV Krick Felix con sus valores numéricos se muestra a continuación [11]:
(11)
Perturbaciones Medioambientales
Como se mencionó anteriormente unas de los mayores problemas a la hora del seguimiento de caminos de vehículos marinos es el efecto de las perturbaciones medioambientales. De estas las que más afectan a los vehículos a la hora de seguir un camino predefinido son: las corrientes marinas y el viento. Por lo antes expuesto se hace necesario contar con una descripción de estas perturbaciones que permitan comprobar el esquema propuesto en este trabajo.
Ecuaciones para Modelar las Corrientes Marinas
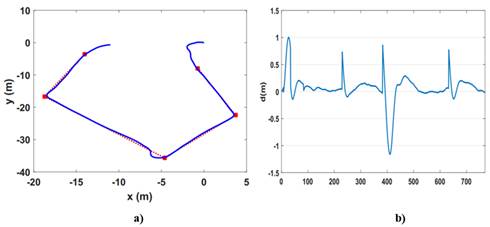
Las corrientes marinas se definen en el sistema de referencia inercial O
e
, considerándose constantes, irrotacionales y acotadas [16]. Para ASV quedan definidas por el vector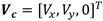 
. El efecto de deriva provocado por las corrientes, mareas, oleajes de baja frecuencia y fuerzas de segundo orden por olas inducidas es incorporado al vector de corriente marinas Vc [17]. Las fuerzas inducidas por las olas de primer orden se ignoran en este contexto, ya que provocan movimientos oscilatorios de media cero que normalmente se eliminan mediante el filtrado de las olas [18]. Es importante tener en cuenta que las corrientes marinas Vc no dependen del rumbo del barco y representan un efecto de deriva cinemático, de hecho, se definen como una deriva de velocidad constante e irrotacional y, por lo tanto, no capturan los efectos perturbadores dependientes del rumbo del vehículo que provocan las corrientes, el viento y las olas [17]. En este trabajo, el vector w es presentado posteriormente para tener en cuenta también estas perturbaciones.
La velocidad de las corrientes marinas de un fluido irrotacional se puede representar en el sistema de referencia del vehículo como (12):
(12)
Donde uc y vc representan las componentes lineales de la velocidad de las corrientes. El efecto de las corrientes marinas se añade al modelo no lineal de 3 GDL del vehículo mediante el término (velocidad relativa). La velocidad relativa se define en el sistema de referencia Ob como (13):
(13)
Siendo v el vector velocidad del vehículo. Cuando se le agregan las corrientes marinas al modelo (ecuación 4), queda de la siguiente manera:
(14)
El vector vc se relaciona con Vc mediante la ecuación (2):
(15)
La magnitud de las corrientes se denota como Vca. La dirección de las mismas, respecto al movimiento de la embarcación, es expresada en función de dos ángulos: el ángulo de dirección vertical (αc) y el ángulo de dirección lateral (βc). Para esta investigación resulta de interés obtener un modelo bidimensional de las corrientes, por lo que únicamente interesan las componentes (uc, vc), considerando que αc = 0. De manera que las ecuaciones para determinar los términos de Vc quedan en función de Vca y de βc [13] (16):
(16)
Las componentes de velocidad de las corrientes referidas a Ob se calculan mediante la ecuación (15)
(17)
Con
El modelo para corrientes marinas constantes e irrotacionales constituye una buena aproximación cuando se implementa un sistema de control a bordo de la embarcación. La utilización de este tipo de modelo es crucial a la hora de seleccionar los objetivos de control, así como para el diseño de algoritmos de guiado.
Ecuaciones para Modelar el Viento
El vector w representa un término de deriva que incorpora dinámicas no modeladas y perturbaciones dinámicas dependientes del rumbo causadas por corrientes, vientos y olas. En este contexto, se supone que el efecto significativo de las perturbaciones constantes del viento domina en w [17]. Se considera el efecto de deriva medio y de variación lenta causado por el viento, mientras que los efectos de media cero altamente oscilantes debidos a ráfagas de viento no se tienen en cuenta, ya que a menudo se eliminan mediante el filtrado de olas. Además, la inercia del vehículo también tiene efectos de filtrado de paso bajo (fig. 3).
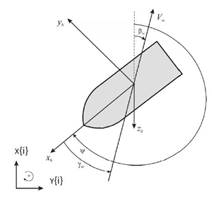
Fig. 3 Definición de la velocidad del viento Vw, dirección del viento βw y su ángulo de incidencia γw.[13].
La incidencia del viento sobre el vehículo se ve determinada a partir de un vector de fuerzas y momentos. Según la Figura 4, se puede apreciar que en este modelo se tienen en cuenta tanto la velocidad del viento como el ángulo con el que incide sobre el barco. Matemáticamente, se expresa según la siguiente ecuación 17:
(18)
Por lo que la ecuación (14) se modifica de la siguiente manera:
(19)
Las expresiones para determinar los valores de γw y VR son:
(20)
(21)
Las componentes de la velocidad del viento relativa al vehículo en las direcciones x-y son:
(22)
donde Vw y βw representan la velocidad y la dirección del viento, definidas en la Figura 4.
Esquema de guiado basado en el algoritmo NLGL
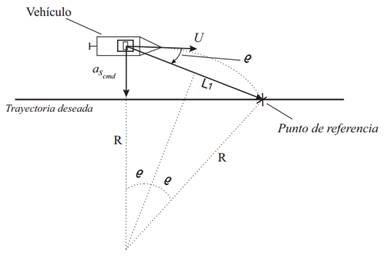
El algoritmo de guiado NLGL se basa en escoger un punto de referencia en la trayectoria deseada y a partir de este generar un comando de aceleración lateral [8]. En la Figura 5 se muestra como el punto de referencia se encuentra a una distancia L1 hacia adelante del vehículo. En la Tabla 3 se presentan las variables que intervienen en el algoritmo.
Tabla 3 Variables del algoritmo de guiado basado en la distancia L1
| Notación | Significado |
|---|---|
| U | Módulo de la velocidad del vehículo |
| L1 | Distancia que separa la posición del vehículo del punto de referencia situado en la trayectoria deseada. |
| ϱ | Ángulo comprendido entre U y la distancia L1 |
| d | Error perpendicular al camino |
|
Comando de aceleración lateral |
| R | Radio del círculo virtual |
El comando de aceleración lateral es el encargado de que el vehículo converja a la trayectoria deseada, a medida que va disminuyendo el error también disminuye la aceleración, llegando al punto de ser cero. Esta acción de mando permite que el vehículo siga el camino deseado. Este comando no es más que la aceleración centrípeta necesaria para seguir el camino circular de radio R definido por la posición del punto de referencia, la posición del vehículo y tangencialmente al vector de velocidad del vehículo como se muestra en la Figura 5. La aceleración lateral queda definida como:
(23)
Como se aprecia en la Figura 4 existe una relación entre la distancia L1 y R que expresada matemáticamente queda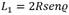 
la cual sustituyéndola en la ecuación (23) se llega a la expresión del comando de aceleración lateral, el cual está determinado por:
(24)
De la ecuación (6) cabe destacar que la dirección de la aceleración depende del signo del ángulo entre la distancia L1 y U. Además, es importante señalar que cuando el vehículo esté alejado del camino, el ángulo ϱ será de mayor amplitud, por lo que la aceleración tendrá un valor elevado, pero cuando el vehículo se encuentre sobre la línea del camino este ángulo tendrá valor cero por lo que no existirá aceleración lateral, siendo así como el algoritmo consigue converger a la trayectoria deseada.
Cabe destacar que el comando de aceleración lateral no coincide con ninguno de los estados presentes en el modelo presentado anteriormente, ecuación (19). Por lo cual es necesario asociar este comando con alguno de los estados del modelo, en este caso la velocidad angular (r). Teniendo en cuenta la ecuación (23) y sabiendo que existe una relación entre la velocidad angular y la velocidad lineal dada por:
(25)
donde r d es la velocidad angular necesaria para que el vehículo siga la circunferencia de radio R a la velocidad lineal U. A partir de las ecuaciones (23 y 25) se obtiene una expresión que relaciona a la velocidad de giro deseada en el movimiento de guiñada con el comando de aceleración lateral:
(26)
De esta manera, a partir del comando de aceleración lateral generado por el algoritmo, resulta posible definir el valor necesario de velocidad angular r d , para que el vehículo sea capaz de seguir un camino previamente definido. Esto da como resultado el esquema de guiado que se muestra a continuación (Figura 5)
Como se puede apreciar el esquema consiste en una estructura en cascada que tiene la posición del vehículo como referencia, el error es la entrada hacia el algoritmo de guiado NLGL que a su vez da la referencia al lazo de control de r.
Linealización del Esquema
Cuando el vehículo se encuentra cerca de la trayectoria a seguir, el valor del ángulo ϱ es pequeño y a pequeñas variaciones del mismo se puede utilizar la aproximación lineal (27):
(27)
De la Figura 7 se puede concluir que:
(28)
(29)
Combinando las ecuaciones 28 y 29 con la (24) se llega a:
(30)
La linealización presentada hace que el algoritmo se comporte como un controlador PD que actúa sobre el error perpendicular al camino. Como se puede apreciar en la ecuación (30), las ganancias proporcional y derivativa del controlador dependen del valor del módulo de la velocidad del vehículo (U) y de la distancia L 1 .
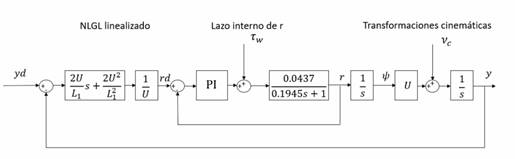
Partiendo de la linealización descrita y del modelo linealizado presentado en la ecuación (11) el esquema de guiado mostrado en la Figura 6 puede ser modificado como se muestra en la Figura 7.
Partiendo de este diagrama se puede apreciar cómo es que las perturbaciones ambientales afectan el sistema. El efecto perjudicial de las corrientes marinas en el seguimiento de caminos dado que influyen sobre el vector de velocidades del vehículo, o sea sobre la cinemática del mismo, es eliminado por las integraciones necesarias para las transformaciones cinemáticas presentes en el esquema. El viento por su parte actúa como un torque sobre la embarcación, o sea, sobre la dinámica del vehículo por lo que es necesario agregar una acción integral en el lazo interno para garantizar cero error de seguimiento de camino.
Análisis de Estabilidad
Para los sistemas no lineales resulta muy difícil realizar un análisis de estabilidad, en ocasiones se hace imposible. El segundo método de Lyapunov se aplica en estos casos donde los otros métodos fracasan. No obstante, a pesar de ser un método muy poderoso no es sencillo de determinar para modelos de gran complejidad por lo que la experiencia cumple un papel importante [20]. Mediante el segundo método de Lyapunov se determina la estabilidad de un sistema sin resolver las ecuaciones de estado, lo que significa una gran ventaja, pues generalmente resulta muy difícil despejar las ecuaciones de estado no lineales. En consecuencia, se procede a realizar el análisis de estabilidad del esquema de guiado basado en el algoritmo NLGL.
Lazo Interno
En primer lugar, se analizará la dinámica de lazo interno donde el modelo presentado en este trabajo presenta no linealidades. Teniendo en cuenta que nuestro sistema de guiado está concebido para seguimiento de caminos, path following, el estado de equilibrio del lazo interno lo logramos con ν = [U, 0, 0] T , donde u = U = constante. Sin embargo, el sistema de guiado no tiene capacidad de modificar la velocidad U. Por lo que para la realización del análisis de estabilidad hacemos coincidir el estado de equilibrio con el origen, por ello hacemos (31):
Por lo tanto, la ecuación (4) se convierte en (32):
(32)
Se asume que la matrix de entrada B es conocida y M , C y D no se conocen. A partir de lo anterior expuesto se selecciona un control PI como controlador, y se tiene la ley de control siguiente:
(33)
donde B † es una matriz pseudoinversa de Moore-Penrose [21] la cual se obtiene como:
(34)
Además, se tiene:
(35)
Se definen como variablesintermedias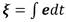 
, 
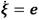y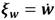 
. Con ello la ecuación de mando (33) quedaría como (36):
(36)
La función candidata de Lyapunov definida positiva es escogida (37):
(37)
La derivada de la función candidata de Lyapunov es (38):
(38)
De acuerdo a las ecuaciones (30) y (35):
(39)
Por lo tanto (38) queda
(40)
De la ecuación (32) se tiene
(41)
Sustituyendo (36) en (41), se tiene (42):
(42)
Sustituyendo (48) en (46) y eliminando términos semejantes se tiene
(43)
Teniendo en cuenta que ν 𝑇 𝑪 𝝂 𝝂=𝟎 para todo 𝝂, entonces (44):
(44)
En la sección 3.2 se define que efecto significativo de las perturbaciones constantes del viento domina en w por lo que 𝝃 𝒘 = 𝒘 =0. Por lo que si al regulador PI propuesto se le realiza una adecuada selección de Ki = KiT > 0 y Kv > 0, la ecuación (44) queda (45):
(45)
Esto significa que la energía es disipada por el amortiguamiento pasivo de la matriz D(v) y por el amortiguamiento activo de la matriz Kv. Entonces aplicando el teorema del conjunto invariante de Krasovskii-LaSalle [21], los valores definidos para 
no contiene ninguna trayectoria que no sea (ν = 0, ξ = 0). Por lo tanto, el sistema es asintóticamente estable siempre que D > 0
Lazo Externo
Para el análisis de estabilidad del algoritmo durante el seguimiento de caminos rectos se tomaron variables de estado que coinciden con las utilizadas en un artículo del autor del algoritmo NLGL, al igual que la candidata de Lyapunov [8]. Primeramente, se deben presentar las siguientes consideraciones iniciales:
En la sección 3.1 se define la velocidad de las corrientes marinas V c . La misma es definida en el sistema de referencia inercial y se asume que es constante, irrotacional, desconocida y acotada, o sea, existe un valor V ca > 0. Entonces cuando se tienen problemas en la navegación relacionados con las corrientes marinas es útil introducir el concepto de velocidad relativa U r que no es más que la velocidad del vehículo con respecto a las corrientes, la misma se obtiene de la siguiente forma [17] (46):
(46)
Una vez definidas la velocidad relativa se puede afirmar que para prevenir que el vehículo quede a la deriva el valor U r debe ser estrictamente mayor que el valor de velocidad de las corrientes marinas. Dicho de otro modo, U r > U ca
Una vez realizadas las aclaraciones anteriores se presentan las variables de estado de nuestro sistema basados en la Figura 6:
(47)
(48)
A partir de la Figura 6 se obtiene la siguiente relación (49):
(49)
La función de Lyapunov propuesta definida positiva es (50):
(50)
Su derivada queda de la siguiente manera (51):
(51)
Con el fin de demostrar que la ecuación (51) es definida negativa, se procede a realizar una serie de pasos: primeramente, se sustituye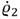 
y 
en la ecuación (51) y utilizando las ecuaciones (24 y 49) se obtiene como resultado:
(52)
Simplificando y agrupando términos semejantes, la ecuación (52) queda:
(53)
Por último, usando la identidad (54)
(54)
La derivada de la función de Lyapunov queda reducida a:
(55)
Siendo esta semi-definida negativa para los rangos de las variables de estado para:
y
Entonces aplicando el teorema del conjunto invariante de Krasovskii-LaSalle [8], los valores definidos para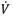 
= 0 no contienen ninguna trayectoria que no sea (ϱ
2
= 0, d = 0). Por lo que el sistema es asintóticamente estable.
Se puede concluir entonces, que el esquema de guiado propuesto durante el seguimiento de caminos rectos, para las condiciones anteriores, es asintóticamente estable.
Resultados de las pruebas Simuladas y Experimentales
En esta sección se presentan los resultados de esta investigación, primero mediante simulación y luego mediante pruebas experimentales. Para las simulaciones se utiliza la estructura de la Figura 5 y el modelo de 3 GDL ecuación (5). La perturbación del viento es generada a partir de la ecuación (18) y las corrientes con la ecuación (16). Para el control se hace uso de la implementación del algoritmo presente en la plataforma Ardupilot [22]. La misma propone calcular la distancia 𝐿 1 a partir de dos parámetros ajustables T y ϕ los cuales son fijados en 8 y 0.75, respectivamente, valores recomendados por Ardupilot [22]. Además, el controlador interno se sintoniza a partir del modelo de Nomoto, ecuación (11), con un PI con valores de P = 2 e I = 0.2, por último, la velocidad de giro del motor se fija a 400 rpm similar a los valores experimentales.
Primeramente, se analiza el esquema simulado en una trayectoria simple conformada por dos puntos (10 10; 60 10) donde se puede analizar el efecto que tienen las diferentes perturbaciones sobre el vehículo a la hora del seguimiento de camino (Fig. 8). En un primer caso se deja fijo el valor de velocidad y dirección del viento de V w = 2 m/s y β w = 10o, y se analiza el comportamiento del seguimiento de caminos ante distintos valores de V ca y así poder apreciar el efecto de las corrientes marinas. En la simulación el valor de V ca al inicio es cero y durante la trayectoria, en el punto (35,10) se le aplica el valor de corriente tipo escalón con un ángulo β c = 90o con diferentes magnitudes. En la Figura 9 se puede apreciar como luego del efecto inicial de la perturbación de corriente el vehículo es sacado de la trayectoria, sin embargo, el mismo converge rápidamente al camino en cada caso con cero error de seguimiento.
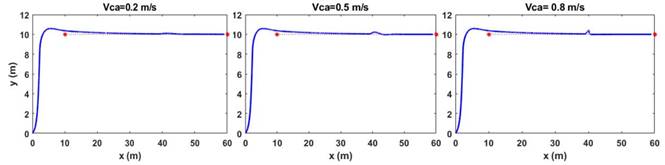
Fig. 8 Seguimiento de camino por parte del bote robótico Krick Felix ante varios valores de perturbaciones de corrientes V ca en el punto (35, 10) mediante simulación.
En la Figura 9 se aprecia el comportamiento del error de seguimiento del camino durante estos experimentos, en la misma se puede apreciar que el mismo disminuye hasta llegar a cero ante el efecto de ambas perturbaciones.
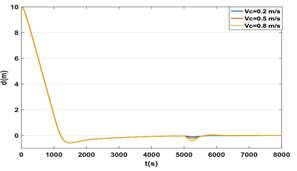
Fig. 9 Error de seguimiento de camino por parte del bote robótico Krick Felix ante varios valores de perturbaciones de corrientes V ca en el punto (35, 10)
En un segundo grupo de simulaciones se repite el experimento anterior solo que ahora se deja fijo el valor de la corriente marina V ca = 0.2m/s y β c = 10o y variamos el valor del viento V w con un ángulo β w = −90o que se introduce en tipo escalón en el punto (10,22). En la Figura 10 se puede apreciar una vez más como luego del efecto inicial de la perturbación el vehículo es sacado de la trayectoria sin embargo el mismo converge rápidamente a la misma en cada caso
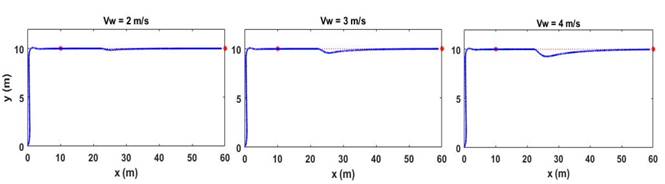
Fig. 10 Seguimiento de camino por parte del bote robótico Krick Felix ante varios valores de perturbaciones tipo vientos Vw en el punto (22, 10) mediante simulación.
En la Figura 11 se aprecia el comportamiento del error de seguimiento del camino durante estos experimentos. En la misma se puede apreciar una vez más que el error disminuye hasta llegar a cero ante el efecto de ambas perturbaciones.
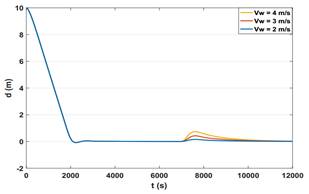
Fig. 11 Error de seguimiento de camino por parte del bote robótico Krick Felix ante varios valores de perturbaciones tipo vientos Vw en el punto (22, 10)
En un segundo momento se realiza una simulación donde el vehículo debe seguir un camino compuesto por varios tramos rectos mientras es afectado por las perturbaciones medioambientales. Los valores de las corrientes serán de V ca = 0.2 m/s con un ángulo β c = 10o, y del viento, V w = 2 m/s con un ángulo β w = 10o.
En la Tabla 4 se puede apreciar la trayectoria deseada que el vehículo debe seguir.
Tabla 4 Puntos del camino
| P1 | P2 | P3 | P4 | P5 | |
|---|---|---|---|---|---|
| x (m) | 8.482 | 12.9 | 4.57 | -9.53 | -4.797 |
| y (m) | -10.04 | -24.58 | -37.76 | -18.82 | -5.647 |
En la Figura 13 se puede apreciar como el vehículo sigue un camino previamente definido en las condiciones antes mencionadas. Además, se aprecia el comportamiento del error de seguimiento del camino durante el experimento, en la misma se puede apreciar que el mismo disminuye hasta llegar a cero ante el efecto de ambas perturbaciones (Fig. 12).
Fig. 12 Seguimiento de un camino compuesto por varios tramos rectos por parte del bote robótico Krick Felix (a) y error de seguimiento del camino mediante simulación (b)
Para validar los resultados de las simulaciones se realizaron pruebas experimentales con el bote robótico Krick Felix. Las mismas se llevaron a cabo en una laguna ubicada cerca del campo universitario de la UCLV, Santa Clara, Cuba, donde existe una corriente natural por el flujo del agua y con condiciones ambientales de viento, aunque estas magnitudes no fueron posibles de medir. Para las pruebas experimentales se utiliza la misma configuración vista anteriormente, tanto en el lazo interno como en la implementación del algoritmo. En la Figura 13 se muestra como el vehículo sigue el camino deseado, a pesar de las perturbaciones ambientales. Además, se puede apreciar el comportamiento del error de seguimiento del camino el cual tiende a cero durante la trayectoria.
Conclusiones
En este trabajo se presentó un esquema de guiado basado en el algoritmo NLGL que consigue cero error de seguimiento de caminos rectos en presencia de múltiples perturbaciones sin la necesidad de la medición del ángulo de guiñada. El mismo presenta un esquema en cascada compuesto por un lazo interno de velocidad angular r que presenta un controlador PI y un lazo externo donde está presente el algoritmo NLGL. Este algoritmo de guiado es muy sencillo de implementar y presenta una gran robustes a la hora del seguimiento de caminos rectos. Una gran ventaja de la estructura del esquema propuesto es que elimina la necesidad una acción integral en el lazo externo, con su consecuente efecto sobre la estabilidad, para eliminar el efecto de las corrientes.
La estabilidad del esquema fue validada a partir del segundo método de Lyapunov donde se tiene en cuenta el efecto de las perturbaciones en la estabilidad del mismo demostrando que el sistema es asintóticamente estable. Por último, fue presentado los resultados de las pruebas simuladas y experimentales donde se comprueba que el esquema propuesto hace que el ASV Krick Felix converja al camino recto predefinido en presencia del efecto de las corrientes marinas y del viento.
