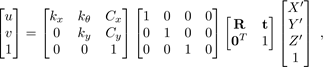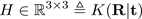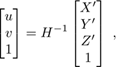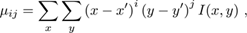Introducción
La mayoría de los robots manipuladores utilizados para fines académicos o de laboratorio están accionados por servomotores denominados de Hobby, los cuales internamente cuentan con un controlador en malla cerrada de posición angular, probablemente del tipo PD. Dichos servomotores reciben comandos de posición angular deseada por medio de diferentes tipos de señales, no obstante, cuando se utilizan para accionar articulaciones de robots están sujetos a perturbaciones como la gravedad, fricción en el tren de engranes, o las fuerzas y pares de reacción provocados por el acoplamiento mecánico entre los eslabones. Por tal motivo, no se puede garantizar que los robots accionados por este tipo de servomotores alcancen los valores deseados de sus articulaciones y, consecuentemente, también se afecta la posición de su efector final en el espacio Cartesiano. En este contexto, se han hecho esfuerzos por mejorar el desempeño de este tipo de robots, por lo que en este trabajo se presenta una técnica para mejorar el control de las articulaciones de robots accionados por servomotores de tipo Hobby, es decir, con actuadores de posición. La estrategia propuesta es el uso de realimentación visual (o visión artificial) para estimar las posiciones articulares e implementar una segunda malla de control que garantice el cumplimiento de las consignas de posición, por lo tanto, se considera que es una estrategia de control basada en visión.
El control de robots basado en visión no es una técnica nueva, ya que se trabaja desde finales de la década de los 70’s [1], y para principios de los 90’s, ya existía un extenso interés por dicho tema [2]. Gracias a los significativos avances de los sistemas electrónicos, con el tiempo se han mejorado también las estrategias de control basado en visión para sistemas robóticos. Un ejemplo notable de principios del presente siglo lo podemos encontrar en [3], en donde se implementó una cámara para realimentar la malla de control de un robot manipulador PUMA 761; los autores utilizaron el modelo de cámara de orificio para relacionar los puntos del plano imagen con el sistema de coordenadas tridimensional, no obstante, se requieren dos cámaras para hacer funcionar ésta tecnología. Asimismo, el creciente desarrollo del software de visión artificial y de hardware dedicado ha contribuido a la implementación de cámaras para el control de robots, como se puede apreciar en [4], en donde se presenta el control de un robot paralelo; dicha contribución que fue posible gracias al software Matlab y a la adquisición de datos con hardware de National Instruments. Sin embargo, la técnica propuesta por los autores requiere que la cámara esté fija y que el eje óptico sea estrictamente perpendicular al plano de movimiento del robot, por lo que el algoritmo de control fallaría al desviar el eje óptico de acuerdo a la prueba de estabilidad que los autores presentan.
La mayoría de los trabajos más recientes continúan utilizando técnicas cinemáticas, propuestas desde el siglo pasado, para el control de robots basado en visión. En [5] se presenta el control para orientar el efector final de un robot ABB IRB 1200 utilizando una cámara montada en dicho efector, en el cual se utiliza el modelo de proyección de la cámara que no es robusto a traslaciones ni rotaciones alrededor de su eje perpendicular a su plano de soporte (ángulo de paneo abusando del lenguaje). Recientemente, en [6] se presenta un trabajo similar de control con la cámara empotrada en el efector final del robot, pero ya se incluye la medición de la profundidad utilizando una cámara RGB-D. Por otra parte, en relación al control de las posiciones articulares con realimentación visual, en un trabajo reciente se presentó el uso del modelo de proyección de la cámara [7], con los inconvenientes de robustez que ya se mencionaron anteriormente. Finalmente, en [8] se presenta un controlador con realimentación visual para un robot manipulador de 4 grados de libertad (GDL); aunque la realimentación visual no usa los parámetros intrínsecos ni extrínsecos de la cámara, para que el controlador funcione correctamente se asume que el plano de la imagen siempre es paralelo al plano del objeto durante el movimiento del robot, por lo que tampoco es una técnica robusta.
De los trabajos revisados y citados anteriormente, se puede observar que existe preferencia por el uso de los modelos cinemáticos y de proyección de la cámara. Sin embargo, existen otros métodos para poder transformar las coordenadas del plano imagen al espacio tridimensional, tal es el caso del uso de matrices de homografía [9].
Dado que un número considerable de robots manipuladores de propósito académico o de laboratorio no cuentan con sensores accesibles para medir las posiciones de las articulaciones, no es posible garantizar que éstas alcancen sus valores deseados por las condiciones del controlador interno de los actuadores de posición. Para hacer frente a este inconveniente, en este trabajo se propone la implementación de una cámara que permite estimar las posiciones articulares a través de la captura y procesamiento de las imágenes obtenidas. Por otro lado, hasta el momento los algoritmos de realimentación visual para control de robots reportados en la literatura carecen de robustez ante traslaciones y rotaciones de la cámara, además de que en el mismo estado del arte se reconoce la carencia de dicha robustez y la insuficiencia de las metodologías que requieren que el eje óptico sea estrictamente perpendicular al plano de movimiento del robot [9]. En este contexto, se pretende mejorar el desempeño de robots manipuladores con actuadores de posición utilizando una técnica de realimentación visual que sea robusta, es decir, que no dependa ni de los parámetros o calibración de la cámara ni de una posición u orientación fijas del eje óptico. Así, considerando la problemática expuesta, el algoritmo propuesto de estimación visual robusta permite crear una malla de control adicional a la que viene empotrada por defecto en los accionadores de las articulaciones del manipulador.
La principal contribución al estado del arte es que la estimación visual propuesta es invariante ante rotaciones de la cámara alrededor de su eje perpendicular a su plano de soporte, lo cuál es una situación común para este tipo de sistemas y representa una solución al problema de estimar correctamente las variables deseadas, en este caso, de las posiciones articulares del robot. Por tal motivo, se considera que el algoritmo propuesto es robusto y representa una ventaja respecto a la estimación visual tradicional ya que no requiere calibración de la cámara ni tampoco que esté siempre fija. Por lo tanto, la estimación visual robusta propuesta incrementa la confiabilidad del sistema de control del robot.
Para dar validez al algoritmo de realimentación visual propuesto, se llevaron a cabo experimentos que consistieron en el envío de diversas posiciones de referencia para las articulaciones del robot bajo las siguientes condiciones: sin realimentación visual y realimentación visual con tres diferentes ángulos de paneo de la cámara. Los resultados se cuantificaron en términos de un índice de desempeño bien conocido en la literatura que se redujo gracias a la realimentación visual, por lo que en efecto se mejora el sistema de control incluido por defecto en el robot, además de que la rotación de la cámara no perjudicó el desempeño de la regulación de posición del robot manipulador. Cabe mencionar que el presente trabajo es una continuación de los resultados obtenidos en [10], contribuyendo en el control a nivel de las articulaciones y presentando un algoritmo más robusto y probado con más experimentos con respecto al trabajo anterior, obteniendo también resultados más contundentes justificados cuantitativamente.
El artículo está organizado de la siguiente forma: primero se describen los materiales y métodos utilizados para los experimentos. Posteriormente, se describe detalladamente el algoritmo de realimentación visual robusto. Después se aborda el sistema de control propuesto para continuar con la descripción de los experimentos y el análisis de los resultados. Finalmente, se presentan las conclusiones de la investigación.
Materiales y métodos
A continuación, se describe el sistema robótico utilizado en esta investigación, así como los componentes de hardware adicionales y el software donde se ejecutaron los algoritmos de control y realimentación visual.
Robot Manipulador
El robot utilizado en esta investigación es un manipulador de tres GDL fabricado con plástico ABS a partir de impresión 3D, cuyo movimiento está restringido únicamente en un plano como se puede observar en la Figura 1, donde también se pueden apreciar los tres eslabones del robot que son l 1 , l 2 y l 3 , además de sus articulaciones q 1 , q 2 y q 3 . Asimismo, se puede observar una distancia d 0 de la base del robot hasta su primera articulación. Las primeras dos articulaciones son de tipo rotacional y cada una está accionada por un servomotor controlado en posición, cuyas entradas de referencia son señales moduladas por ancho de pulso (PWM); dichas señales cuentan con una amplitud de 0 a 5 V y con un periodo de 20 ms, del cual el ciclo de trabajo puede variar de 1 a 2 ms para mapear comandos de referencia entre 0° y 270°. La segunda articulación, cuenta con un mecanismo conformado por dos eslabones auxiliares, propiamente l 2a y l 2b , mismo que transmite el movimiento rotacional del servomotor al eslabón l 2 , tal como se ilustra en la parte izquierda de la Figura 2. La última de las articulaciones, que también es rotacional, no cuenta con accionamiento por servomotor, sin embargo, el eslabón acoplado a dicha articulación permanece siempre horizontal debido al accionamiento indirecto que le proveen las dos primeras articulaciones por medio de un mecanismo conformado por los eslabones l 2c , l 3a , l 3b y l 3c , tal como se observa en la Figura 2. De esta manera, el valor de la articulación q 3 está dado por (1)
Cabe mencionar que la posición horizontal del tercer eslabón puede llegar a tener una variación de hasta 5° debido al juego mecánico de las barras paralelas del manipulador. Por último, se colocaron marcadores de diferentes colores en las articulaciones del robot y en su efector final, con el objetivo de utilizarlos en el proceso de estimación visual de sus valores.
Hardware y Software Implementados
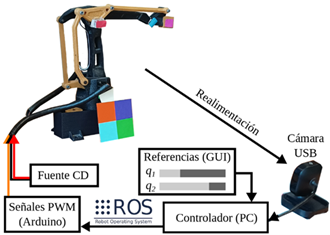
Para el proceso de adquisición de las imágenes que se utilizan en la realimentación visual se implementó una cámara web modelo Microsoft LifeCam VX-800, la cual cuenta con un sensor de captura tipo CMOS VGA; su resolución es de 640 x 480 px, su campo de visión tiene 59° de apertura y además es autoajustable a las condiciones de luz. Las imágenes se adquirieron con dicha cámara a 30 cuadros por segundo (FPS por sus siglas en inglés) y se procesaron en una PC con procesador Intel Core i7 con 8 GB de memoria RAM, cuyo sistema operativo es Ubuntu 20.24; asimismo, los algoritmos de control se ejecutaron en dicha PC. Adicionalmente, se implementó la tarjeta Arduino Mega 2560 para generar las señales PWM que accionan los servomotores del robot a partir de las consignas de control calculadas desde la PC. También se utilizó una fuente externa de 5 V a 2 A para alimentar dichos servomotores. En la Figura 3 se ilustra un diagrama con todos los componentes de Hardware mencionados para llevar a cabo la presente investigación.
Por otra parte, para ejecutar los algoritmos de estimación visual robusta y de control se utilizó el lenguaje de programación Python 3.8.10 junto con la librería OpenCV 4.7.0, la cual es útil para implementar los algoritmos de procesamiento y análisis de imágenes. También se utilizó lenguaje C++ para programar, en el microcontrolador Arduino Mega, el algoritmo que transforma las consignas de control de las articulaciones del robot en señales PWM. La comunicación entre la PC y el Arduino Mega se realizó por medio del Sistema Operativo para Robots (ROS por sus siglas en inglés), el cual es un middleware que unifica la comunicación entre sensores, actuadores, robots, etc., sin importar el medio de transmisión de datos (USB, ethernet, WiFi, etc.). Por último, se desarrolló una interfaz gráfica de usuario (GUI por sus siglas en inglés) en lenguaje Python, en la cual se visualiza la imagen procesada y a su vez cuenta con dos comandos deslizadores para cambiar los ángulos de referencia de las posiciones articulares del robot.
 Derecha: Manipulador en estudio con sus parámetros geométricos.
Derecha: Manipulador en estudio con sus parámetros geométricos.Figura 1 Izquierda: Fotografía del robot manipulador de 3 GDL.
 Derecha: eslabones involucrados en el accionamiento del eslabón 3.
Derecha: eslabones involucrados en el accionamiento del eslabón 3.Figura 2 Izquierda: eslabones involucrados en el accionamiento del eslabón 2.
Estimación visual robusta
A continuación, se detalla el procedimiento de estimación de las posiciones articulares del robot por medio de la realimentación visual. Dicha estimación se caracteriza por ser robusta con respecto a las rotaciones de la cámara, es decir, las mediciones de las posiciones articulares no cambian si se rota la cámara y, por consecuencia, varía la perspectiva de las imágenes adquiridas.
Modelo de la Proyección en Perspectiva
Considerar un punto [u, v]∈ℕ 2 captado por una cámara, el cuál se denomina “punto escena”, mismo que corresponde a un punto [X’,Y’,Z’]∈ℝ 3 en el referencial del mundo. La expresión que relaciona dichos puntos (salvo un factor de escala) está dada por la transformación homogénea [11]
donde k x , k y , k 𝜃 , C x , C y ∈ℝ son los parámetros intrínsecos de la cámara relacionados con la fabricación del chip captador, R ∈SO (3) es la matriz de rotación y t ∈ℝ 3 es el vector de traslación que expresan el movimiento entre el referencial del mundo y el referencial del captador. La expresión (2) se conoce como modelo de proyección en perspectiva. Diversos trabajos han utilizado este modelo para obtener información de las variables a controlar de los sistemas robóticos, sin embargo, este modelo es susceptible a rotaciones y traslaciones de la cámara ya que habría que conocer los valores de los desplazamientos para incluirlos en el modelo. Por tal motivo, en la siguiente sección se describe el algoritmo para robustecer la correspondencia entre los puntos captados por la cámara y su equivalente en el referencial del mundo.
Corrección de la Perspectiva de la Imagen
Una alternativa al modelo de la Proyección en Perspectiva es mapear los puntos colineales entre dos planos proyectivos por medio de una transformación lineal llamada homografía [11]. Dicha operación se puede realizar por medio de la matriz homogénea cuadrada (3)
con K∈ℝ 3×3 es una matriz que contiene los parámetros de la cámara. La aplicación de la matriz de homografía a las coordenadas homogéneas del plano imagen para obtener su equivalente en el referencial del mundo se conoce como corrección de la perspectiva, matemáticamente se puede expresar como
Se puede observar que las expresiones (2) y (4) son casi equivalentes, sin embargo, la matriz de homografía puede obtenerse sin los datos de la calibración de la cámara, basta con asignar un vector de cuatro coordenadas conocidas en el espacio tridimensional (sin profundidad) a una correspondencia de cuatro puntos en el plano imagen. En la Figura 4 se ilustra cómo se llevó a cabo la corrección en perspectiva de las imágenes adquiridas del manipulador. Se observa el patrón utilizado, para obtener H por medio de la librería OpenCV, el cual consiste en un cuadrado de 8×8 cm con cuatro colores distintos, de los cuales se obtiene su centroide en el plano imagen; a dichos puntos se les asigna una correspondencia en el espacio tridimensional utilizando las medidas conocidas del patrón. Con la matriz de homografía se realiza la corrección en perspectiva, misma que da robustez a ligeras rotaciones de la cámara; una vez corregida la perspectiva, se procede a procesar los cuadros recuperados con la cámara para posteriormente detectar objetos de interés. Esta técnica se ha utilizado para detectar objetos en el espacio de trabajo de robots manipuladores con resultados satisfactorios [12].
Procesamiento de la Imagen Corregida en Perspectiva
Como se mencionó anteriormente, cada articulación cuenta con un marcador de diferente color, mismo que puede ser identificado y seguido en cada cuadro adquirido por la cámara. Para lograr este objetivo, se realizaron técnicas de procesamiento en las imágenes adquiridas. Una vez que se ha corregido la perspectiva de la imagen por medio de la homografía, se procede a hacer un cambio en el espacio de color. Las imágenes adquiridas se encuentran en el espacio de tres canales azul-verde-rojo (BGR por sus siglas en inglés), por lo que se transforman al espacio matiz-saturación-valor (HSV por sus siglas en inglés) con el objetivo de simplificar la sintonización de los parámetros de la segmentación de color, la cual consiste en asignar un rango de valores entre 0 y 255 que corresponden al color que se desea identificar. Por tal motivo, en el espacio BGR habría que sintonizar 3 valores correspondiendo a la selección de 6 umbrales (3 altos y 3 bajos), en cambio en el espacio HSV se sintoniza un solo valor (2 umbrales) para elegir el color a identificar. La sintonización de los dos parámetros restantes, saturación y valor, también se realizó, pero el rango de valores adecuados es amplio y no representa la misma dificultad que sintonizar los 6 umbrales BGR.
Una vez seleccionados los umbrales, se genera una segunda imagen en blanco y negro a la cual se mapean los píxeles de la imagen a color; aquellos píxeles que se encuentran dentro del rango de color seleccionado se mapean con un valor de 255 o color blanco. En cambio, aquellos píxeles que se encuentran fuera de los umbrales establecidos se mapean con valor de 0 o color negro; a este proceso se le denomina “binarización” y se aplica para cada uno de los cuatro marcadores debido a que son de colores distintos. Finalmente, dado que pueden existir píxeles en la imagen que se encuentren fuera de los marcadores (ruido) se implementó un filtro de la mediana para eliminarlos, de tal modo que la nueva imagen cuenta con valores en blanco únicamente en el área de los marcadores.
Detección de los Marcadores
Una vez que los marcadores fueron segmentados por color, se procede a calcular el centroide de cada uno de ellos en el espacio de la imagen, lo cual tiene una correspondencia con el espacio Cartesiano gracias a la corrección en perspectiva realizada anteriormente. En este contexto, sea F(x,y) la imagen binaria que cuenta con un único objeto blanco I(x,y) sobre un fondo negro; los momentos centrales del objeto, en este caso los marcadores, están dados por [10] (5)
los cuales son invariantes a traslaciones. Con dichos momentos se pueden obtener los centroides de los objetos por medio de las expresiones
La Figura 5 ilustra el ejemplo de la detección del color verde por medio de las etapas de procesamiento descritas anteriormente, en donde se aprecia primeramente la binarización, en este caso, para identificar el marcador de color verde. Se puede observar que aún existe ruido en la imagen, es decir, objetos de color blanco, por lo que se aplica el filtro de la mediana y, posteriormente, se emplean las ecuaciones (5), (6) y (7) para obtener el centroide del marcador, el cual será de utilidad para estimar las posiciones articulares del robot. Finalmente, para efectos de visualización, se marcan tanto el centroide como el contorno del objeto en la imagen a color. En la Tabla 1 se presenta la correspondencia entre los colores de los marcadores y los centroides calculados.
 Central: imagen filtrada. Derecha: Imagen a color con el color verde seleccionado.
Central: imagen filtrada. Derecha: Imagen a color con el color verde seleccionado.Figura 5 Ejemplo del procesamiento de las imágenes para la detección de un color. Izquierda: imagen binarizada con presencia de ruido.
Tabla 1 Correspondencia entre color de marcador y centroides.
| Color | Cxi | Cyi |
|---|---|---|
| Verde | 1 | 1 |
| Rojo | 2 | 2 |
| Azul | 3 | 3 |
| Magenta | 4 | 4 |
Estimación de las Posiciones Articulares
Cuando se han identificado todos los marcadores, es posible calcular los ángulos que hay entre cada uno de ellos, mismos que corresponden a las posiciones articulares del robot. Las expresiones para calcular dichos ángulos son [13], (8), (9), (10)
En la Figura 6 se ilustra la imagen capturada original y la imagen a color de donde se obtienen los valores estimados de las articulaciones del manipulador.
Control de las articulaciones
Ya que se cuenta con la información sobre los valores articulares del robot, es posible implementar un controlador en malla cerrada que garantice que las articulaciones lleguen a una posición deseada. Dada la naturaleza discreta de la realimentación, se propone la siguiente ley de control. (11)
donde n = 1,2 es el número de articulación, en(k)=qnd(k)-qn(k) es el error de posición en el ciclo k; 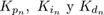 son constantes positivas, T es el periodo de muestreo y ξ
n
(k) es la integración numérica del n-ésimo error de posición dada por (12)
son constantes positivas, T es el periodo de muestreo y ξ
n
(k) es la integración numérica del n-ésimo error de posición dada por (12)
Para seleccionar el periodo de muestreo T utilizado en el controlador (11) se consideró, primeramente, la tasa de adquisición de las imágenes que en este caso es de 30 FPS. Posteriormente, se midió un tiempo de ejecución de todo el algoritmo de realimentación visual de aproximadamente 96 ms, por lo que se consideró un periodo de muestreo de 100 ms para el controlador (11) y así garantizar que se hayan completado las mediciones de las articulaciones. Las ganancias utilizadas se ilustran en la Tabla 2, las cuales se obtuvieron experimentalmente utilizando el método de sintonización empírica basada en reglas descrito en [14].
En la Figura 7 se presenta el diagrama a bloques del sistema de control con realimentación visual para la n-ésima articulación, en donde se puede apreciar que dicha realimentación representa una segunda malla de control, recordando que cada articulación cuenta con su propio controlador en malla cerrada. La dependencia de k se omite por simplicidad en dicho diagrama. De esta manera, el controlador PID (11) tiene como salida la posición angular de referencia para el servomotor, es decir u n (k) = q n ref (k).
Tabla 2 Ganancias del controlador (11) para cada articulación.
| Constantes |
|
|
|---|---|---|
| K
|
0.6 | 0.3 |
| K
|
0.03 | 0.01 |
| K
|
0.06 | 0.02 |
Experimentos y resultados
Para comprobar la efectividad de la realimentación robusta, se realizaron los siguientes experimentos: primero, se le enviaron comandos de posición a las articulaciones del robot en malla abierta, es decir, sin implementar la ley de control (11), esto con el objetivo de contrastar los comportamientos del robot en ausencia y en presencia del control usando la realimentación visual desarrollada. Posteriormente, se enviaron comandos de posición aplicando el controlador en malla cerrada y con diferentes ángulos de paneo de la cámara, esto con el objetivo de mostrar la robustez del algoritmo propuesto. Los videos de los experimentos se pueden encontrar en el siguiente link: https://youtu.be/keCvGHUu5YU, mismos que se detallan a continuación.
Comandos de Posición sin Realimentación
El primer experimento consistió, como se mencionó anteriormente, en suministrar comandos de posición a las articulaciones del robot a partir de su posición de Home, es decir, q 1 =q 2 =90°. Primero se comandaron referencias a la primera articulación y, posteriormente, se le cambió la referencia a la segunda, esto para mostrar dos aspectos: primeramente, que las articulaciones no llegan a la referencia deseada; segundo, el efecto de las perturbaciones que genera el movimiento del primer eslabón al segundo. La Figura 8 muestra los resultados del experimento. Se puede observar que la primera articulación trata de alcanzar las referencias deseadas, pero siempre presentando error de hasta 10°. Por otra parte, se puede apreciar que, en efecto, el movimiento del primer eslabón perturba al segundo, pero también se observa que el controlador local de la segunda articulación no compensa los errores de posición ocasionados por dicha perturbación.
Comandos de Posición utilizando Realimentación Visual Robusta
Los experimentos siguientes se realizaron utilizando la malla de realimentación visual robusta propuesta en este trabajo. Se comandaron diferentes posiciones para ambas articulaciones. En la Figura 9 se presentan los resultados del experimento. En ella es posible observar que la primera articulación converge a las referencias asignadas. Observando la parte derecha de la Figura se aprecia como la segunda articulación converge a las posiciones deseadas a pesar de las perturbaciones ocasionadas por los movimientos del primer eslabón.
Comandos de Posición Variando el Ángulo de la Cámara
El siguiente experimento consistió en variar el ángulo de paneo de la cámara para verificar la robustez de la realimentación, es decir, las mediciones de los ángulos deben ser invariantes a la rotación de la cámara y, por consiguiente, el controlador debe funcionar bajo estas condiciones. En la Figura 10 se ilustra cómo se llevó a cabo la rotación de la cámara a ±10°; inevitablemente no solo existe rotación, sino también hay traslación de la cámara. Primeramente, con la cámara rotada 10°, se comandaron posiciones de referencia a ambas articulaciones, cuyos resultados se presentan en la Figura 11. Observando dicha Figura se observa que las articulaciones convergen a las referencias o a vecindades cercanas de hasta 1°, a pesar de las perturbaciones ocasionadas por el acoplamiento mecánico de los eslabones. Posteriormente, se comandaron referencias a las articulaciones pero ahora utilizando la realimentación visual con rotación de -10°. Los resultados del comportamiento de las articulaciones se presentan en la Figura 12, donde de la misma manera, se observa que las articulaciones convergen a las referencias o retoman el valor asignado después de ser perturbadas.

Figura 8 Comportamiento de las articulaciones cambiando de referencias sin la malla de realimentación visual. Izquierda: primera articulación. Derecha: segunda articulación. Las unidades del eje vertical son grados. Las unidades del eje horizontal son segundos.
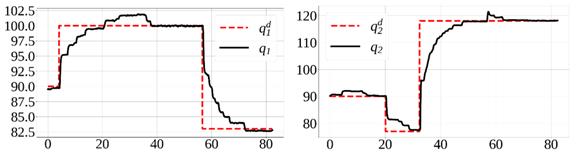
Figura 9 Comportamiento de las articulaciones cambiando de referencias utilizando la malla de realimentación visual. Izquierda: primera articulación. Derecha: segunda articulación. Las unidades del eje vertical son grados. Las unidades del eje horizontal son segundos.
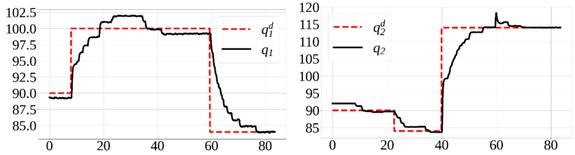
Figura 11 Comportamiento de las articulaciones cambiando de referencias utilizando la malla de realimentación visual con la cámara rotada 10°. Izquierda: primera articulación. Derecha: segunda articulación. Las unidades del eje vertical son grados. Las unidades del eje horizontal son segundos.
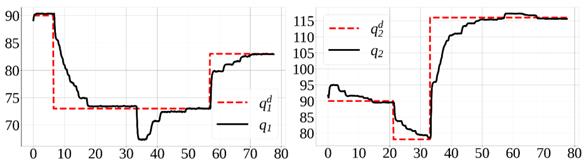
Figura 12 Comportamiento de las articulaciones cambiando de referencias utilizando la malla de realimentación visual con la cámara rotada -10°. Izquierda: primera articulación. Derecha: segunda articulación. Las unidades del eje vertical son grados. Las unidades del eje horizontal son segundos.
Análisis de Resultados
Considerando la Figura 8, se puede observar que las articulaciones no convergen a las referencias deseadas en ausencia de la malla de realimentación visual. Por otro lado, en la Figura 9 se puede apreciar que las posiciones articulares convergen a los valores de referencia asignados, o a valores muy cercanos, a pesar de las perturbaciones ocasionadas por el acoplamiento entre eslabones. De igual manera en las Figuras 11 y 12 se aprecia la convergencia de las posiciones articulares a las consignas de control, sin importar la rotación de la cámara y las perturbaciones mencionadas anteriormente. En este sentido, se considera que la segunda malla de control funciona adecuadamente y en efecto mejora el desempeño del control de posición del robot.
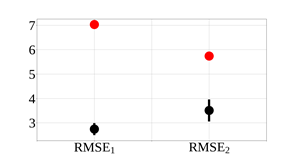
Con el objetivo de cuantificar el desempeño del sistema de control propuesto basado en la realimentación visual robusta, se utilizó el índice de desempeño conocido como raíz del error cuadrático medio (RMSE por sus siglas en inglés) para cada articulación, dado por la siguiente expresión (15)
Con dicho índice se puede apreciar la efectividad de un sistema de control, considerando que éste es mejor mientras menor sea el valor del índice. Primeramente, se calculó el RMSE de cada articulación para el experimento sin realimentación visual y, posteriormente, se calculó para cada uno de los experimentos con realimentación visual, por lo que también se obtuvo la media y la desviación estándar de dichos experimentos. En la Figura 13 se ilustran los RMSE de las articulaciones 1 y 2, en donde se puede observar que, gracias a la realimentación visual, se redujo el RMSE en ambos casos.
Conclusiones
En este trabajo se presentó una técnica de realimentación visual robusta para mejorar el sistema de control de un robot manipulador con actuadores controlados en posición. En este sentido, el objetivo es garantizar que se alcance el valor deseado de las posiciones articulares, por lo que se implementó una segunda malla de control utilizando visión artificial.
La realimentación visual se implementó para medir las posiciones de las articulaciones del robot manipulador enfocado en el plano imagen de la cámara. Se considera que la realimentación es robusta debido a que las mediciones de las posiciones articulares son invariantes a rotaciones de paneo y a traslaciones de la cámara con respecto al plano imagen alineado con el referencial del robot, lo cual se logró por medio de una corrección de perspectiva en tiempo real y utilizando segmentación de colores para la detección de las articulaciones.
Se realizaron diferentes experimentos en el robot manipulador para verificar el funcionamiento y la efectividad de la estrategia de control con realimentación visual propuesta: primero se enviaron comandos de posición a las articulaciones del robot sin utilizar dicha realimentación visual. Posteriormente, se enviaron comandos de posición cerrando la malla y rotando la cámara. Se graficaron los resultados del control de posición y se calculó el RMSE de cada articulación con los diferentes experimentos realizados.
Como resultado, se redujeron significativamente los errores de posición por medio de la segunda malla de control basada en visión. Además, se comprobó la robustez del sistema de visión debido a que el índice de desempeño utilizado se redujo y no presentó variación significativa cuando se realizaron los experimentos de control de posición con rotación de la cámara. En este contexto, se considera que los resultados obtenidos son satisfactorios, ya que se logró reducir los errores de posición de las articulaciones del robot a pesar de las perturbaciones ocasionadas por el acoplamiento mecánico de los eslabones, sin importar que la cámara no estuviese perfectamente alineada con el referencial del robot. Por tal motivo, se considera que el uso de la técnica presentada es una alternativa útil para mejorar el control de robots cuyas articulaciones están accionadas por servomotores. Se pretende mejorar ésta técnica para que pueda ser aplicable a robots con movimiento en tres dimensiones.