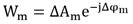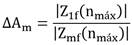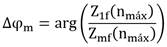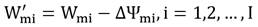Artículo de investigación

Implementación en FPGA de la Calibración de un Sistema de Antenas Inteligentes con Superresolución en la Estimación de DOA

Smart Antennas System FPGA Calibration Implementation with Super Resolution DOA Estimation

0000-0002-0538-4053Yunior Ibarra Guerra^{1  *}  , 0000-0002-8884-320XNoslen Rojas Ramírez¹  , 0000-0002-0372-0746Alexander R. Ramírez Zaldívar¹  , 0000-0001-6886-3871Abel Hernández Violat¹ 

¹ Centro de Investigación y Desarrollo de Electrónica y Mecánica, “CID MECATRONICS”, La Habana, Cuba

RESUMEN

La calibración de los errores de amplitud y fase de los canales receptores en las antenas inteligentes resulta un proceso crucial para alcanzar los requerimientos del sistema. La implementación de estas funciones en un dispositivo programable y los procedimientos para la selección de sus parámetros, no es un tema ampliamente divulgado en la literatura especializada. Este trabajo soluciona la problemática anterior a partir de la implementación en FPGA del algoritmo de calibración en función de las exigencias para garantizar la estimación de la dirección de arribo (DOA, por sus siglas en inglés) con superresolución. El diseño implementado en Lenguaje de Descripción de Hardware (HDL, por sus siglas en inglés) corrige en tiempo real los errores de amplitud y fase entre canales del sistema de recepción multicanal con una baja latencia y consumo de recursos. La comprobación experimental con señales reales demuestra que los errores obtenidos luego de la calibración se encuentran en el rango esperado y corrobora la efectividad del diseño.

Palabras-clave: DOA; Calibración, Antenas Inteligentes; FPGA, FFT

ABSTRACT

Receiver channels amplitude and phase calibration in smart antennas is a crucial process to achieve the systems requirement. The implementation of these functions in a programmable device and the procedures for selecting its parameters is not a widely disseminated topic in the specialized literature. This work solves the previous problem by implementing the calibration algorithm in FPGA based on the requirements to guarantee the estimation of the direction of arrival (DOA) with super resolution. The design implemented in Hardware Description Language (HDL) corrects in real time the amplitude and phase errors between channels of the multichannel reception system with low latency and resource consumption. Experimental verification with real signals demonstrates that the errors obtained after calibration are within the expected range and corroborates the effectiveness of the design.

Key words: DOA; Calibration; Smart Antennas; FPGA; FFT

Introducción

Los servicios de comunicaciones inalámbricas experimentan un crecimiento sin igual desde los últimos años debido a la introducción de nuevas generaciones de sistemas de comunicaciones móviles como la 5G [1-5] y la carrera por el dominio de la 6G ^[1, ⁶, ⁷, ^8]. En la actualidad, el centro de atención cambia drásticamente hacia los servicios de datos por encima de los de voz y se conciben como sistemas multipropósito que podrán proporcionar control, computación, servicios de comunicación, localización y detección para el usuario (3CLS, por sus siglas en inglés) ^[7, ^9]. El desarrollo de estas tecnologías presupone un reto a las infraestructuras existentes, a lo que se suman los problemas propios de un sistema inalámbrico como lo constituyen: el desvanecimiento por la propagación multitrayecto, el ruido térmico y la interferencia cocanal ^[10, ¹¹, ^12].

Los sistemas de antenas inteligentes se consideran una tecnología clave para mitigar los problemas anteriores a la hora de proporcionar servicios de datos de alta velocidad ^[1, ¹³, ^14]. Entre los beneficios relacionados con su empleo resaltan el aumento de la cobertura y la capacidad, la conmutación inteligente, una mejor calidad del servicio, la seguridad de la información y el acceso a la ubicación del usuario ^[1, ^14]. Esta tecnología combina múltiples elementos de antenas con el procesamiento espacio-temporal de señales para optimizar su patrón de radiación en función del entorno radioeléctrico circundante ^[13]. Dos procesos fundamentales que tienen lugar son la estimación de la dirección de arribo (DOA, por sus siglas en inglés) y la formación digital del patrón de radiación. La estimación de DOA, por lo general, utiliza algoritmos de superresolución ^[15] para adaptarse a las necesidades actuales de saturación espectral y elevado número de usuarios. Su principal ventaja radica en que permiten obtener resoluciones superiores al ángulo de radiación del arreglo de antenas y robustez para procesar señales cocanales ^[12, ^16].

Tanto el problema de estimación de DOA como el de formación del haz poseen una dependencia directa de la amplitud y fase de las señales recibidas de cada uno de los elementos del arreglo de antenas. A pesar de sus probadas ventajas ^[18], los métodos de estimación de DOA con superresolución poseen el inconveniente de ser más sensibles a los errores de amplitud y fase de los canales receptores ^[19]. La presencia de tales errores ocasiona desajustes entre el modelo de las señales, lo que resulta en una disminución del rendimiento de la estimación o incluso el fallo del algoritmo ^[19, ²⁰, ^21].

Varios factores impactan de manera negativa en los errores de amplitud y fase de los receptores multicanales coherentes para un sistema de antenas inteligentes. Inconsistencia de los componentes, tolerancia de la fabricación, errores de montaje, reemplazo de partes, influencia mutua entre los elementos, temperatura del entorno, entre otros, resultan los más significativos ^[17, ²², ^23]. Para mitigar tales efectos, el sistema de recepción debe someterse de antemano a un riguroso proceso de calibración de amplitud y fase. La adecuada selección de los parámetros de diseño y una efectiva implementación del método de calibración permiten que tanto la estimación de DOA como la formación digital del patrón de radiación alcancen los requerimientos previstos ^[23].

En ^[1] se propone un algoritmo para la estimación de DOA basado en aprendizaje semisupervisado en presencia de deficiencias de hardware, donde la DOA se estima a través de dos pasos: aprendizaje de diccionario y mapeo. En su mayoría se utilizan datos sin etiquetar y requiere una pequeña cantidad de datos etiquetados con condiciones de fácil adquisición. Los resultados de la simulación muestran que el algoritmo propuesto mantiene una alta precisión bajo graves deterioros del hardware y aunque argumentan que permite una implementación práctica, no se detallan sus particularidades.

En ^[24] se propone un nuevo arreglo de antenas en fase de banda S para estaciones terrestres satelitales en órbita LEO. Se utilizó el algoritmo de proyección inversa para calibrar el patrón de ganancia de la antena en un escaneo de campo cercano. El sistema de antenas en fase propuesto se demostró con éxito en el satélite de órbita terrestre baja KOMPSAT-5 operado por Corea del Sur. Este método de calibración, al igual que el que se propone en ^[25], posee la desventaja de requerir condiciones especiales para su implementación, por lo que no es capaz de considerar los desajustes y variaciones que ocurren durante el funcionamiento. Además, aunque se menciona que la placa de alimentación y control está diseñada sobre la base de un microcontrolador y una FPGA, no se detallan las funciones específicas de cada uno ni el algoritmo implementado.

En [26] se presenta una descripción completa del método de calibración externa de los transceptores y elementos de un arreglo lineal para el radar denominado AgileDARN ^[26]. Los desequilibrios de amplitud y fase de los transceptores se calibran con éxito inyectando de forma interna dos señales de secuencias multipulso con la misma amplitud y fase. El algoritmo explota los ecos de los meteoritos desde la parte superior de la mesosfera y termosfera inferior, considerados fuentes de señales de oportunidad distantes, de una perspectiva de los arreglos de antenas. Este método de calibración utiliza un ajuste de mínimos cuadrados lineal para procesar las señales en cuadratura I/Q sin procesar. Los resultados medidos se han utilizado para ilustrar el excelente rendimiento de la metodología y demostrar que es estadísticamente eficiente. No obstante, la adopción de este tipo de señal patrón presenta particularidades que no permite extenderse de manera sencilla a otras aplicaciones.

En ^[27] se propone un nuevo método de calibración de los errores de amplitud-fase y estimación de DOA 2D aplicable en los enjambres de drones que vuelen a igual altura y que pueden comportarse como arreglos planos. El método se basa en el empleo de un método de minimización de normas atómicas desacopladas (DANM, por sus siglas en inglés) y el método de descenso de gradiente. La solución propuesta permite estimar de manera simultánea los errores y la DOA inicial en 2D (acimut y elevación). Las simulaciones se evalúan utilizando un arreglo plano coprimo de antenas ^[28] y los resultados demuestran que el método puede lograr una mayor precisión de estimación en comparación con otros métodos convencionales. Se proporciona una nueva metodología para investigaciones posteriores sobre la estimación de DOA 2D bajo errores de ganancia y fase. No obstante, se obvian varios problemas prácticos que pueden emerger, como son el intercambio, sincronización y coherencia de muestras de múltiples plataformas y la factibilidad de una implementación en tiempo real de las técnicas de optimización descritas.

Varios trabajos han presentado nuevos métodos de calibración y es un tema tratado exhaustivamente en la literatura científica ^[29], no obstante, no ha sido el caso de su implementación práctica ^[19, ²⁷, ³⁰, ^31]. Trabajos como los que se presentan en ^[32, ³³, ³⁴, ^35] se centran en la calibración del acoplamiento mutuo entre elementos del arreglo de antenas con la suposición de que los canales receptores se encuentran calibrados, lo que por lo general no es una suposición práctica ^[23]. Soluciones como los que se proponen en ^[9] se centran en aspectos teóricos sin considerar que este tópico concierne también a elementos físicos. La mayoría de las soluciones propuestas evalúan su rendimiento mediante simulaciones numéricas, lo que en muchos casos no considera la totalidad de los efectos ni las complejidades del hardware. Solo unos pocos autores extienden los métodos teóricos a un diseño real y evalúan su rendimiento con señales reales ^[21, ³⁴, ^36].

Aunque el empleo de los FPGA experimenta un crecimiento creciente en el desarrollo de antenas inteligentes ^[24, ^37], poco se divulga del diseño de los algoritmos de calibración en este tipo de dispositivos programables. En ^[38] se propone un método de calibración de fase basada en el algoritmo Computadora Digital para Rotación de Coordenadas(CORDIC, por sus siglas en inglés) y se implementa en un dispositivo FPGA Virtex-5. Los resultados experimentales concluyen que la precisión del algoritmo es de 0.49º cuando se emplean 20000 muestras de señal, valor que puede ser prohibitivo para varias aplicaciones en tiempo real ^[8]. Además, no se argumenta bajo qué criterios se selecciona este valor, ni la SNR de las señales involucradas, además de no considerar la calibración de la amplitud. Los criterios de selección de los parámetros de la señal patrón, como son la SNR y el número de muestras, rara vez son expuestos, a pesar de que varios autores resaltan que son factores decisivos en el rendimiento de la calibración ^[19, ³⁰, ³⁶, ³⁹, ^40].

El objetivo de este trabajo es presentar la implementación en FPGA de la calibración de los canales receptores de un sistema de antenas de inteligentes con superresolución en la estimación de DOA. Además, se propone un procedimiento para la determinación de los parámetros del módulo de calibración enfocado en cumplir las exigencias con los recursos mínimos indispensables. El diseño implementado en HDL permite la corrección de los errores de amplitud y fase entre canales del sistema de recepción multicanal. La solución se enfocó en obtener una baja latencia para afectar al mínimo la disponibilidad del sistema. La validación experimental del diseño con señales reales demuestra que la implementación cumple con las exigencias planteadas y corrobora el procedimiento de diseño adoptado.

Las contribuciones científicas fundamentales que se hacen en este trabajo son:

1. Implementación en FPGA de la calibración de un sistema de antenas inteligentes.

2. Un procedimiento para la determinación de los parámetros del módulo de calibración en función de las exigencias.

3. La adopción de un esquema de calibración paralelo con módulos FFT optimizados.

4. La validación experimental de la calibración y la estimación de DOA con señales reales.

Calibración de los canales receptores de un sistema de antenas inteligentes

Para realizar la calibración de los canales del arreglo de antenas es necesario un equipamiento de monitoreo que debe incluir una fuente de señal excitadora, una red de acoplamiento de la trayectoria de calibración y un dispositivo de control y cálculo de los coeficientes de calibración. En función de las ubicaciones de la trayectoria de acoplamiento, los métodos de calibración pueden clasificarse en métodos de calibración interna y métodos de calibración externa ^[36, ^39], tal como muestra la figura 1. En la variante interna, la señal de calibración se acopla de forma directa a los canales receptores, mientras que en la segunda, esta se transmite con una antena externa al arreglo de antenas ^[35]. Cada variante tiene sus ventajas y desventajas cuyos detalles se abordan con más profundidad en ^[17].

Independientemente del método empleado, el sistema de procesamiento debe realizar funciones similares para el cálculo de los pesos de calibración, cuyos métodos y esquemas se han abordado de manera extensiva en la literatura ^[17, ²⁵, ²⁹, ³⁰, ³⁵, ^41]. En el siguiente epígrafe se detalla el procedimiento adoptado por la mayor parte de las referencias consultadas.

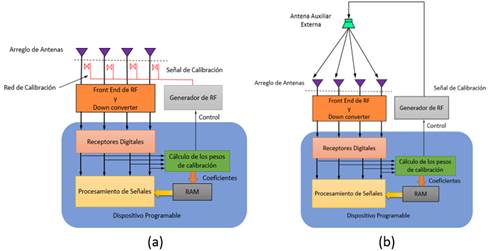
Figura 1 Esquema ilustrativo del proceso de calibración de los canales receptores del arreglo de antenas. a) Calibración interna. b) Calibración externa. 

Proceso de calibración de los canales receptores de un sistema de antenas inteligentes

Dado un arreglo de antenas de M canales, una vez que se obtienen N muestras complejas de la señal de calibración para el m-ésimo canal de recepción Zm, el error de fase para cada canal puede estimarse de varias formas de acuerdo con la literatura relacionada ^[21, ²⁶, ³⁶, ³⁸, ⁴¹, ⁴², ⁴³, ^44]. Una de las más empleadas se basa en la aplicación de la FFT a la señal patrón ^[36, ⁴¹, ⁴², ⁴³, ^44] y la otra emplea el procesamiento temporal de las componentes en cuadratura de fase ^[21, ²⁶, ³⁸, ^43]. La adopción de la FFT posee la ventaja de que las señales patrón mono frecuencia se superponen coherentemente, a diferencia del ruido blanco, lo que incrementa el valor de la SNR ^[36]. En este trabajo se tomará como referencia la variante de la FFT, aunque puede aplicarse a otros métodos con cambios mínimos. Si se toma el primer canal como referencia, el coeficiente de calibración del m-ésimo canal W_m se calcula de acuerdo a la expresión (1), (2) y (3)

(1)

(2)

(3)

Donde Z_1f y Z_mf constituyen la salida de la FFT de N_fft puntos de las muestras Z₁ y Z_m respectivamente. La variable n_máx representa el punto del valor máximo del valor absoluto del espectro de frecuencias y arg(∙)denota el argumento de un número complejo. Debido a que el retardo de fase ∆Ψ de la red de calibración no está presente en el canal durante el modo normal de trabajo, el vector de los coeficientes de calibración finales en la i-ésima frecuencia de trabajo debe corregirse de acuerdo a la expresión (4).

(4)

Si los errores de amplitud y fase de las muestras calibradas se encuentran en el rango permisible, la calibración se detiene y se almacena W´_i en una memoria RAM. En caso contrario, debe realizarse nuevamente el proceso hasta alcanzar los valores permisibles sin sobrepasar un aproximado de 5 iteraciones ^[43]. Valores máximos de errores de amplitud y fase típicos se consideran de 5^∘ y 1 dB ^[21, ³¹, ^45].

Diseño e implementación en fpga del módulo de calibración de los errores de amplitud y fase entre canales

La implementación del bloque de calibración requiere de una etapa previa que permita determinar sus parámetros de diseño, como el número de puntos de la FFT (N_FFT, relacionado con el número de muestras) y la SNR de la señal patrón, cuyos criterios de selección no es un tema que por lo general se abunde en la literatura ^[36, ^40]. En ^[36] se expresa de forma empírica que una señal de calibración con un valor de SNR de alrededor de 40 dB permite alcanzar los resultados esperados tanto para el proceso de estimación de DOA como para la formación digital del patrón de radiación. No obstante, no se justifica este criterio ni la repercusión en el diseño del sistema. Debido a que estas magnitudes poseen una relación no lineal sin expresión analítica conocida, se obtuvo un procedimiento basado en el empleo de la simulación para determinar estos valores, cuyo diagrama de flujo se muestra en la figura 2.

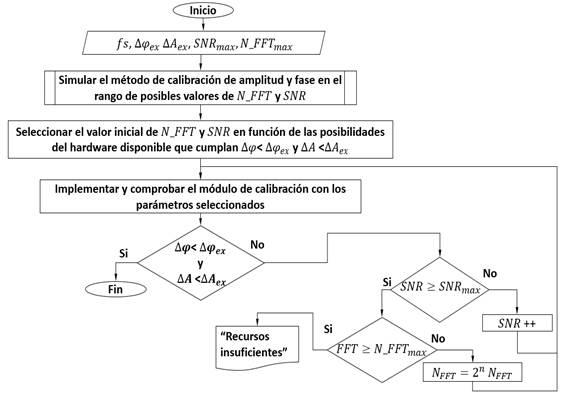
Figura 2 Diagrama de flujo del procedimiento obtenido para determinar los parámetros de diseño del bloque de calibración. 

Una vez seleccionados los valores de SNR y N_FFT, se procedió a implementar el módulo de calibración para un dispositivo FPGA de Intel mediante el flujo de diseño basado en modelos de Simulink y utilizando el toolbox HDL Coder de Matlab 2014b ^[46]. El esquema en bloques del módulo implementado se muestra en la figura 3. El algoritmo de la FFT se programó con el bloque sintetizable de Simulink FFT HDL Optimized v.2014 y se adoptó un esquema paralelo donde cada canal de recepción se procesa de manera independiente. La adopción de este módulo de FFT posibilitó que el diseño estuviera enfocado a una implementación en HDL con baja latencia y recursos de hardware.

Figura 3 Diagrama funcional del sistema de calibración implementado en FPGA. 

A la salida de la FFT del primer canal se implementó el cálculo del valor absoluto y la búsqueda del punto de frecuencia n_máx, correspondiente al valor máximo del espectro. La diferencia en amplitud entre canales se obtuvo a partir de la magnitud de la FFT en n_máx y la diferencia de fase a partir del argumento de las componentes reales e imaginaria. Los pesos de calibración, denominados W_m(m=0,1,…,M) (m=0,1,…,M) y compuestos tanto por las diferencias de amplitud como las de fases, se aplican mediante la multiplicación compleja conjugada con las señales recibidas. En la figura 4 se muestra el diagrama en bloques de la captura esquemática en Quartus Prime 17.0.

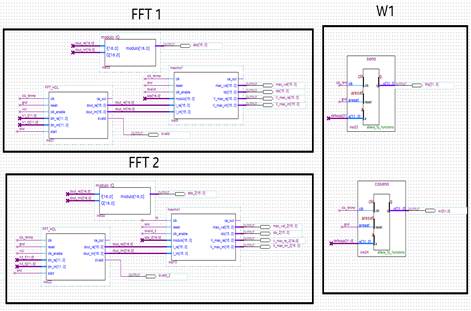
Figura 4 Captura esquemática de la implementación en Quartus Prime 17.0 del diseño de cálculo de los pesos de calibración. 

Una vez obtenidos los coeficientes de los pesos complejos de calibración, estos se aplican al canal de recepción correspondiente mediante un producto complejo conjugado cuya captura esquemática se muestra en la figura 5, en este caso, para las señales procedentes del tercer canal de recepción. La latencia del cálculo de los coeficientes y aplicación de los pesos resultó de 89.4 μs a la frecuencia de reloj de 5 MHz.

Figura 5 Captura esquemática en Quartus Prime 17.0 del bloque empleado para la aplicación de los pesos de calibración. 

Resultados y discusiones

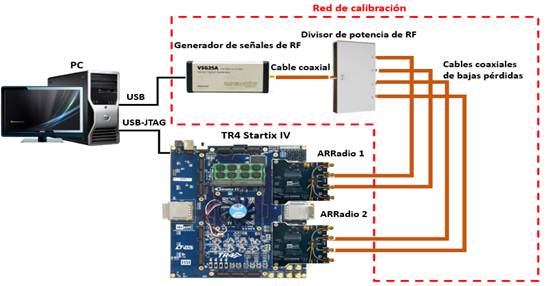
Para la validación del módulo obtenido, se empleó un sistema de recepción coherente de cuatro canales de radiofrecuencia mostrado en la figura 6. La recepción y conversión análogo-digital de las señales se realizó mediante la placa de evaluación ARRadio, la cual porta un transceptor integrado de microondas de dos canales AD9361. El diseño obtenido en HDL se implementó en una FPGA Intel Stratix IV sobre la placa de desarrollo TR4 con una frecuencia de reloj de 5 MHz. La red de calibración se estructuró por un generador vectorial de señales VSG25A, un divisor de potencia de radiofrecuencia de cuatro puertos y cables coaxiales de bajas pérdidas.

Figura 6 Esquema funcional de la red de calibración implementada 

La coherencia del sistema de recepción multicanal se verificó mediante el error de amplitud y fase entre canales, resultante luego de la aplicación de la calibración interna. Con este fin, se empleó el esquema funcional que se muestra en la figura 7.

Figura 7 Esquema funcional de la red de calibración implementada. 

En el generador vectorial de señales VSG25A se estableció una señal sinusoidal con una frecuencia de 2.4003 GHz y una amplitud de -40 dBm. Se configuraron los transceptores AD9361 para operar a través del oscilador local externo y se estableció la coherencia del muestreo multicanal a partir de la configuración de los registros de sincronismo multi-chip (MCS, por sus siglas en inglés) para una frecuencia de muestreo de 5 MHz ^[47]. Como oscilador local externo se empleó el generador de señales de radiofrecuencia EXG N173B con una potencia de salida de 10 dBm para obtener el valor recomendado a la entrada de los osciladores locales cada ARRadio independiente ^[47] luego de la salida del divisor de potencia de radiofrecuencia. Se estableció una ganancia de 50 dB a los 4 receptores y un ancho de banda de radiofrecuencia de 1 MHz.

En la figura 6 se muestra una captura de la adquisición de señales en tiempo real del analizador embebido Signal Tap II Logical Analyzer de Quartus Prime 2017 ^[48] de las señales de calibración a la salida de los AD9361 en su estado inicial. En un gráfico de amplitud discreta (columna izquierda) en función de las muestras temporales, se representan las componentes en fase(I) en banda base. Las sinusoides recibidas poseen una frecuencia en banda base de 300 kHz y muestreadas a 5 MHz.

La figura 6 a) muestra las señales de calibración recibidas en el estado inicial luego de la configuración de los AD9361. Aunque las señales no poseen significativas diferencias de amplitud entre canales, las diferencias de fase son considerables. Como resultado se corrobora la necesidad de la aplicación de la calibración al sistema de recepción. La figura 8 b) muestra el resultado de la corrección en amplitud y fase de la señal patrón luego de la calibración.

Se aprecia el efecto de la calibración debido a que la fase inicial de cada canal se establece a partir del primero, lo que permite la coherencia completa del sistema. Este procedimiento se repitió para las frecuencias en el rango de 2.4 GHz a 2.5 GHz con una discreción de 2 MHz.

Durante las pruebas experimentales se comprobó que el rango de variación de la amplitud para cada frecuencia fue mínimo (en el rango de 0.4 dB). Sin embargo, el error de fase tanto en el encendido inicial del sistema como en los cambios de frecuencia es significativo. En la figura 9 a) se muestra el error de fase obtenido antes de aplicar la calibración.

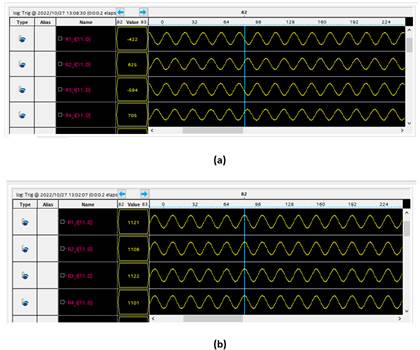
Figura 8 Captura en el analizador lógico Signal Tap de las componentes en fase de los cuatro receptores. a) Antes de aplicar la calibración de amplitud/fase, b) Luego de aplicar la calibración de amplitud/fase. 

Figura 9 Error de fase de los canales de recepción. a) Antes de la calibración para cada una de las frecuencias de trabajo. b) Luego de la calibración para cada una de las frecuencias de trabajo. 

En este caso, la raíz del error cuadrático medio (RMSE, por sus siglas en inglés) de la diferencia de fase resultó de 70º. En la figura 8 b) se muestra el resultado de la aplicación de la calibración del desbalance en amplitud y fase de los canales receptores, cuyo valor medio de error de fase final resultó de 2.6º. Estos valores se consideran en correspondencia con la literatura acerca del tema ^[21], no obstante, su impacto se evaluó en el proceso de estimación de DOA con superresolución. Con este fin, las muestras de las señales antes y después de la calibración de los canales receptores se exportaron a Matlab para evaluar su comportamiento. Se simuló el método MUSIC ^[49] con 1000 muestras para un arreglo lineal uniforme (ULA, por sus siglas en inglés) de 4 elementos separados a media longitud de onda y un paso de 0.125 º. En la figura 10 se muestra el espectro de MUSIC obtenido para el caso de las señales antes y después de la calibración.

Figura 10 Espectro de MUSIC obtenido antes y después de aplicada la calibración del sistema de recepción del sistema de antenas inteligentes. 

Como se aprecia en el primer caso, el espectro espacial no presenta un pico definido y aparecen múltiples lóbulos como resultado de la incoherencia entre canales ^[36] por lo que es imposible determinar la dirección de la fuente emisora simulada. En el segundo caso, se forma un pico espectral en la dirección de 0º con más de 35 dB de diferencia en la magnitud con respecto al resto de las direcciones (SLL_MUSIC), lo que permite determinar con precisión la dirección de la fuente emisora simulada. Los resultados anteriores demuestran la efectividad del sistema implementado, incluso supera los resultados alcanzados en otros trabajos como se representa en la tabla 1.

Tabla 1 Rendimiento de la calibración de amplitud y fase del método propuesto comparado con otras fuentes 

Referencia	[36]	[24]	[50]	[26]	[38]	Propuesto
Fase(º)	-	2.5	10	1	0.49	2.6
Amplitud(dB)	-	0.28	0.5	0.2	-	0.5
SLL_MUSIC(dB)	-30	-	-	-	-	-35
N	500		-		20000	1000
SNR(dB)	10		-			30
DOA RMSE (º)						0.125
Latencia(us)	-	-	-	-	-	89.4

En ^[36] el rendimiento se expresó en función del nivel del espectro de MUSIC en las direcciones de no incidencia de señal, que en este caso resultó de 30 dB. No obstante, se emplean la mitad de las muestras y una menor SNR, aunque se emplea una fuente emisora externa cuya implementación posee limitaciones prácticas ^[17]. Con respecto al resto de los trabajos, se presentan resultados similares y superiores en algunos casos ^[50]; el menor error de fase alcanzado se presenta en ^[38] pero con el inconveniente de emplear un elevado número de muestras (20000) que para las tasas de muestreo típicas puede repercutir en la estacionariedad de las señales de fuentes emisoras con alta movilidad además de la respectiva latencia que representa. La latencia de 89.4 μs obtenida resulta conveniente para una implementación en tiempo real debido a que la alta coherencia del AD9361 hace que este tiempo repercuta al mínimo comparado con el intervalo entre calibraciones sucesivas. Este resultado permite una alta disponibilidad del sistema y una interrupción mínima de su ciclo de trabajo por concepto de calibración.

En la tabla 2 se muestra el uso lógico de los algoritmos implementados en la FPGA Stratix 4 EP4SGX230KF40C2. A modo de resumen, el diseño requirió un 8% de la lógica, un 1% de la memoria interna dispositivo y el 7% de bloques DSP de 18 bits.

Tabla 2 Uso de recursos de la implementación en FPGA 

Recurso	Empleado	Disponible	Utilización
ALUT combinacionales	9177	182400	5 %
Registros lógicos dedicados	13420	182400	7 %
ALM(completos y parciales)	91200	8260	9 %
LAB(completos y parciales)	930	9120	10 %
Bits de bloques de memoria	65024	14625792	< 1%
Bloques DSP de 18 bits	96	1288	7 %

Los resultados se consideran satisfactorios debido a que brinda un amplio margen para la implementación del resto de los algoritmos relacionados con la estimación de DOA y formación de haces e incluso posee un menor consumo lógico que la propuesta que se presenta en [38]. Esta solución se enfocó en priorizar la mínima latencia posible debido a que el tiempo de calibración afecta la disponibilidad del sistema. En caso de requerir menos recursos, es posible adoptar un esquema serie o combinado de pipeline con empleo de un menor número de canales de procesamiento a costa de un incremento de los recursos de almacenamiento y latencia. También es posible adoptar la síntesis del HDL en herramientas nativas de alto nivel como Intel HLS o DSP Builder para las FPGA de Altera-Intel o Vivado HLS y System Generator para las familias de Xilinx-AMD. Otra variante de disminuir los recursos necesarios resulta del empleo de una mayor SNR a costa de reducir el número de muestras de la señal patrón, lo que es una relación de compromiso durante la etapa de diseño. En este caso es útil la adopción del procedimiento propuesto para buscar un punto de equilibrio satisfactorio. La implementación en HDL fue integrada y validada con éxito anteriormente en un sistema de estimación de DOA con superresolución ^[51] y un radio cognitivo consciente de la ubicación ^[52].

Conclusiones

En este trabajo se propuso la implementación en FPGA de la calibración del sistema de antenas inteligentes enfocado a obtener superresolución en la estimación de DOA. Además, se presentó un procedimiento para determinar los parámetros del módulo de calibración para establecer una relación de compromiso entre la SNR y el número de muestras de la señal patrón en función de cumplir las exigencias de una aplicación específica con los recursos de hardware mínimos. El diseño implementado en HDL corrige en tiempo real los errores de amplitud y fase entre canales del sistema recepción multicanal mediante la adopción de un esquema de calibración con varios módulos de FFT optimizados en paralelo. La solución propuesta se enfocó en minimizar la latencia en pos de afectar al mínimo la disponibilidad del sistema, no obstante, un esquema serie o combinado puede implementarse con cambios mínimos a costa de un posible aumento del consumo de recursos. El empleo del flujo de diseño basado en modelos de Simulink para la síntesis del diseño en HDL facilita la integración en un dispositivo FPGA en un período de tiempo relativamente corto, además de facilitar que la solución se extienda a otras familias de FPGA con mínimos cambios. El consumo de recursos lógicos del dispositivo FPGA utilizado brinda un amplio margen para la implementación de los métodos de formación de haces y estimación de DOA del sistema de antenas inteligentes además de que se encuentra en correspondencia con otros resultados e incluso con un menor requerimiento. La validación de la implementación con señales reales corrobora la funcionalidad del diseño mediante la disminución de los errores de amplitud y fase a valores permisibles y su impacto en la estimación de DOA con superresolución en más de un sistema práctico.

Referencias

1.  Ruan N., Wang H., Wen F., Shi J. DOA Estimation in B5G/6G: Trends and Challenges. Sensors. 2022;22(14):5125-5139. doi: 10.3390/s22145125.

2.  Ashish P. Sparse Linear Antenna Arrays: A Review. In: Hussain A-R, Said A, editors. Antenna Systems. Rijeka: IntechOpen; 2021. p. Ch. 6.

3.  Wittig S., Schmieder M., Keusgen W., Inzunza E. Direction-of-Arrival Measurement of Beamformed Millimeter Wave 5G Downlink Signals. IEEE Radio and Wireless Sysmposium. San Antonio; USA; 2020.

4.  Abdelbari A., Bilgehan B. A novel DOA Estimation Method of Several Sources for 5G Networks. 2020 International Conference on Electrical, Commucation and Computer Engeniering (ICECCE). Istambul; Turkey; 2020. p. 1-6. doi: 10.1109/icecce49384.2020.9179306.

5.  Gashema G., Lee J.-M., Kim D.-S. Efficient-spectrum management based on localisation of primary user position towards 5G. IET Communications. 2020;14(20):3567-3577. doi: 10.1049/iet-com.2020.0284.

6.  Deepanramkumar P., Jaisankar N. BlockCRN-IoCV: Secure Spectrum Access and Beamforming for Defense Against Attacks in mmWave Massive MIMO CRN in 6G Internet of Connected Vehicles. IEEE Access. 2022;10(1):74220-74243. doi: 10.1109/ACCESS.2022.3187745.

7.  Saad W., Bennis M., Chen M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Network. 2020;34(3):134-142. doi: 10.1109/MNET.001.1900287.

8.  She C., Sun C., Gu Z., Li Y., Yang C., Poor H. V., et al. A Tutorial of Ultra-Reliable and Low-Latency Communications in 6G: Integrating Theoretical Knowledge into Deep Learning. Proceedings of the IEEE. 2021;109(3):204-246.

9.  Cheng M., Peng W., editors. Gibbs Sampling Based Sparse Bayesian Learning for Direction-of-Arrival Estimation with Impulse Noise Towards 6G. 2023 IEEE International Conference on Communications Workshops (ICC Workshops) Rome; Italy . 2023;.

10.  Wang H., Lyu X., Liao K. Co-Channel Interference Suppression for LTE Passive Radar Based on Spatial Feature Cognition. Sensors . 2022;22(1):117-135. doi: 10.3390/s22010117.

11.  Wu C., Krishnasamy D., Elangage J. Hardware Implementation and RF High-Fidelity Modeling and Simulation of Compressive Sensing Based 2D Angle-of-Arrival Measurement System for 2-18 GHz Radar Electronic Support Measures. Sensors. 2021;21(20):6823-6850. doi: 10.3390/s21206823.

12.  Saeed N., Nam H., Al-Naffouri T. Y., Alouini M.-S. Primary User Localization and Its Error Analysis in 5G Cognitive Radio Networks. Sensors . 2019;19(9):2035-2048. doi: 10.3390/s19092035.

13.  Misra G., Agarwal K., Agarwal A., Kuntal Ghosh S. A. Smart Antenna for Wireless Cellular Communication - A Technological Analysis on Architecture, Working Mechanism, Drawbacks and Future Scopes. Second International conference on IoT in Social, Mobile, Analytics and Cloud (I-SMAC 2018). Palladam; India.; 2019. p. 37-41.

14.  Ahmed E. Q., Ameen Z. H., Al-Mukhtar F. S., Jaaz Z. A. Maximizing Mobile Communication Efficiency with Smart Antenna Systems using Beam forming and DOA Algorithms. 10th International Conference on Electrical Engineering, Computer Science and Informatics. Barcelona; Spain; 2023. p. 453-460. doi: 10.1109/EECSI59885.2023.10295948.

15.  Kassir H. A., Rekanos I. T., Lazaridis P. I., Yioultsis T. V., Kantartzis N. V., Antonopoulos C. S., et al. DOA Estimation for 6G Communication Systems. 12th International Conference on Modern Circuits and Systems Technologies. Athens; Greece; 2023. p. 1-4. doi: 10.1109/MOCAST57943.2023.10176899.

16.  Yang X., She Y., Xie L., Li Z. Channel state information-based multi-dimensional parameter estimation for massive RF data in smart environments. EURASIP Journal on Advances in Signal Processing. 2021; 2021 (1):16. doi: 10.1186/s13634-021-00724-8.

17.  He G., Gao X., Zhang R. Impact Analysis and Calibration Methods of Excitation Errors for Phased Array Antennas. IEEE Access . 2021;9(1):59010-59026. doi: 10.1109/ACCESS.2021.3073222.

18.  Pesavento M., Trinh-Hoang M., Viberg M. Three More Decades in Array Signal Processing Research: An optimization and structure exploitation perspective. IEEE Signal Processing Magazine. 2023;40(4):92-106. doi: 10.1109/MSP.2023.3255558.

19.  Dai Z. A.-O., Su W., Gu H. Gain-Phase Errors Calibration for a Linear Array Based on Blind Signal Separation. Sensors . 2020;20(15):4233-4245. doi: 10.3390/s20154233.

20.  Dai Z., Su W., Gu H., Li W. Sensor gain-phase errors estimation using disjoint sources in unknown directions. IEEE Sensors Journal. 2016;16(10):3724-3730. doi: 10.1109/JSEN.2016.2531282.

21.  Oliveira M. T., Miranda R. K., Costa J. P. C. L., Almeida A. L. F., Sousa R. T. Low Cost Antenna Array Based Drone Tracking Device for Outdoor Environments. Wireless Communications and Mobile Computing. 2019;2019(1):1-14. doi: 10.1155/2019/5437908.

22.  Friedlander B. The Mythical Uniform Linear Antenna Array. 55th Asilomar Conference on Signals, Systems, and Computers. Califronia, USA; 2021. p. 221-225. doi: 10.1109/IEEECONF53345.2021.9723400.

23.  Friedlander B. On the Mutual Coupling Matrix in Array Signal Processing. 54 th Asilomar Conference on Signals, Systems, and Computers. California; USA; 2020. p. 1245-1249. doi: 10.1109/IEEECONF51394.2020.9443338.

24.  Lee D.-H., Seo J.-W., Lee M.-S., Chung D., Lee D., Bang J.-H., et al. An S-Band-Receiving Phased-Array Antenna with a Phase-Deviation-Minimized Calibration Method for LEO Satellite Ground Station Applications. Electronics. 2022;11(23):3847-3862. doi: 10.3390/electronics11233847.

25.  Pan C., Ba X., Tang Y., Zhang F., Zhang Y., Wang Z., et al. Phased Array Antenna Calibration Method Experimental Validation and Comparison. Electronics . 2023;12(3):489-504. doi: 10.3390/electronics12030489.

26.  Deng X., Lan A. L., Yan J. Y., Wu L., Wu J., Zhang J. J., et al. Calibrating the amplitude and phase imbalances in AgileDARN HF radar. Radio Science. 2021;56(5):1-16. doi: 10.1029/2020RS007138.

27.  Bai X., Qiu H., Zou Z., Huang P., Huang Y., Wang Y. Joint Gain-Phase Errors Calibration and 2D DOA Estimation for Sparse Planar UAV Arrays. IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC). Chongqing; China; 2023. p. 1272-1277. doi: 10.1109/ITOEC57671.2023.10291325.

28.  Ma P., Li J., Xu F., Xiaofei Z. Hole-Free Coprime Array for DOA Estimation: Augmented Uniform Co-array. IEEE Signal Processing Letters. 2020;28(1):36-40. doi: 10.1109/LSP.2020.3044019.

29.  Fu H., Wang Y., Dai F. Off-Grid Error Calibration for Single Snapshot DOA Estimation Based on Sparse Bayesian Learning. 5th International Conference on Information Communication and Signal Processing (ICICSP). Shenzhen; China; 2022. p. 46-50. doi: 10.1109/ICICSP55539.2022.10050710.

30.  Jin X., Wang X., Hou Y., Tian Y. Gain-phase Error Self-calibration DOA Estimation Method Based on Sparse Bayesian. IEEE 6th International Conference on Electronic Information and Communication Technology (ICEICT). Qingdao; China; 2023. p. 658-663. doi: 10.1109/ICEICT57916.2023.10245464.

31.  Al-Dabbagh M. D., Gaber A., Omar A. Phase Calibration of Massive MIMO System for Directiom of Arrival Applications. 2019 IEEE MTT-S International Microwave Conference on Hardware and Systems for 5G and Beyond(IMC-5G). Atlanta; USA; 2019. p. 1-3.

32.  Famorij O. J., Ogundepo O., Qi X. An Intelligent Deep Learning-Based Direction-of-Arrival Estimation Scheme Using Spherical Antenna Array With Unknown Mutual Coupling. IEEE Xplore 2020;8(1):179259-179251. doi: 10.1109/ACCESS.2020.3027623.

33.  Osman H., Bray J. R., editors. Estimation and Compensation of Array Mutual Coupling Using the Sequential Loading Method. 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Toronto; Canada . 2020;.

34.  Khan S., Sajjad H., Ozdemir M. K., Arvas E., editors. Mutual Coupling Compensation in Receiving Arrays and Its Implementation on Software Defined Radios. 2020 International Applied Computational Electromagnetics Society Symposium (ACES) California; USA. 2020;.

35.  Linder M., Meinecke B., Schwarz D., Waldschmidt C. Avoidance of Near-Field Influences in Calibration Measurements of Radars by Means of Active Calibration Targets. 20th European Radar Conference (EuRAD). Berlin; Germany; 2023. p. 383-386. doi: 10.23919/EuRAD58043.2023.10289548.

36.  Wang M., Wang Z., Cheng Z. Joint calibration of mutual coupling and channel gain/phase inconsistency using a near-field auxiliary source. IEEE 13th International Conference on Signal Processing (ICSP). Chengdu; China; 2016. p. 394-398. doi: 10.1109/ICSP.2016.7877862.

37.  Ramírez Zaldívar A. R., Rojas Ramírez N., Hernández Violat A., Ibarra Guerra Y., Peña Sierra A. Implementación en FPGA del procesador para un sistema de antenas con monopulso. Ingeniería Electrónica, Automática y Comunicaciones. 2023;44(1):17-30.

38.  Rajagopalan P., Dubey S., Arora R., Mehta S. D. CORDIC Based Phase Calibration Algorithm for Phase Coherent DSP Applications. 7th International Conference on Signal Processing and Integrated Networks (SPIN). Noida; India; 2020. p. 576-580. doi: 10.1109/SPIN48934.2020.9070821.

39.  Wang F., Jiang R., Tian X., Liu X., Jiang S., Gu B., et al. An Efficient Near-Field Model Gain-Phase Self-Calibration Method for Uniform Rectangular Arrays. IEEE Journal of Oceanic Engineering. 2022;47(4):1129-1142. doi: 10.1109/JOE.2022.3164721.

40.  Ni M., Xiao S., Chen H., editors. A Cascade Calibration of Near-Field Source Gain and Phase Errors. IEEE 3rd International Conference on Signal and Image Processing (ICSIP); Shenzhen; China. 2018.

41.  Hou Y., Shang H., Yang M., Jin C. Method of multichannel calibration for unmanned aerial vehicle surveillance radar. The Journal of Engineering. 2019;2019(21):7864-7867. doi: 10.1049/joe.2019.0651.

42.  Xiong J., Hong H., Zhang H., Wang N., Chu H., Zhu X. Multitarget Respiration Detection With Adaptive Digital Beamforming Technique Based on SIMO Radar. IEEE Transactions on Microwave Theory and Techniques. 2020;68(11):4814-4824. doi: 10.1109/TMTT.2020.3020082.

43.  Zhang W., Yang M., Chen B., Lin Y., Wang J., editors. A phase error calibration method for distributed VHF radar system. 2016 CIE International Conference on Radar (RADAR); Guangzhou; China. 2016.

44.  Nuteson T. W., Stocker J. E., Clark J. S., Haque D. S., Mitchell G. S. Performance characterization of FPGA techniques for calibration and beamforming in smart antenna applications. IEEE Transactions on Microwave Theory and Techniques . 2002;50(12):3043-3051. doi: 10.1109/TMTT.2002.805151.

45.  Eberhardt M., Eschlwech P., Biebl E. Investigations on antenna array calibration algorithms for direction-of-arrival estimation. Advances inRadio Science . 2016;14(1):181-190. doi: 10.5194/ars-14-181-2016.

46.  Kintali K., Gu Y., Cigan E. Model-Based Design Using Simulink, HDL Coder and DSP Builder for Intel FPGAs. In: MathWorks, editor. 2014.

47.  Analog Devices. AD9361 Reference Manual. ANALOG DEVICES; 2020.

48.  Intel Corp. Design Debugging with the Signal Tap Logic Analyzer. Intel Quartus Prime Standard Edition Handbook. 3: Intel Corp.; 2022.

49.  Schmidt R. O. Multiple Emitter Location and Signal Parameter Estimation. IEEE Transactions on Antennas and Propagation. 1986;34(3):276-280. doi: 10.1109/TAP.1986.1143830.

50.  Tengbo C., Lu Z., Hailong D. An Amplitude-phase Measurement Method of Phased Array Antenna Based on Self-Calibration RF Channel. 10th International Conference on Communication Software and Networks (ICCSN). Chengdu, China; 2018. p. 460-464. doi: 10.1109/ICCSN.2018.8488296.

51.  Ibarra Guerra Y., Ramírez Zaldívar A. R., Hernández Violat A., Rojas Ramírez N. Implementación Hardware-Software de un Sistema de Estimación de DOA con Superresolución. Ingeniería Electrónica, Automática y Comunicaciones . 2022;43(1):17-30.

52.  Ibarra Guerra Y., Ramírez Zaldívar A. R., Hernández Violat A., Rojas Ramírez N. Sistema de Estimación de Dirección de Arribo para un Radio Cognitivo Consciente de la Ubicación. Revista Telemática. 2022;21(2):12-26.

Recibido: 08 de Enero de 2024; Aprobado: 08 de Abril de 2024

^* Autor para la correspondencia: [e-mail]

No existe conflicto de intereses entre los autores, ni con ninguna institución a la que cada uno está afiliado, ni con ninguna otra institución.

Yunior Ibarra Guerra: Conceptualización, Software, Metodología, Validación -Verificación, Redacción - revisión y edición.

Noslen Rojas Ramírez: Conceptualización, Supervisión, Metodología, Redacción - Revisión.

Abel Hernández Violat: Metodología, Investigación, Validación -Verificación.

Alexander R. Ramírez Zaldívar: Metodología, Investigación, Validación -Verificación.

Yunior Ibarra Guerra, es ingeniero en Telecomunicaciones, graduado del ITM “José Martí” en el año 2015. Obtuvo el título académico de Máster en Sistemas Digitales en la Universidad Tecnológica de la Habana “José A. Echeverría” en el año 2023. En la actualidad opta por el grado científico de Doctor en Ciencias Técnicas en el ITM “José Martí”. Trabaja en el Centro de Investigación y Desarrollo de Electrónica y Mecánica, “CID MECATRONICS”, La Habana, Cuba. Correo electrónico: [e-mail], No. ORCID: 0000-0002-0538-4053. Sus principales intereses de investigación son el procesamiento de señales de arreglos de antenas, los radios cognitivos y el diseño en lógica programable.

Noslen Rojas Ramírez, es Ingeniero Radioelectrónico, graduado en el ITM "José Martí" en el año 1994. Máster en Radioelectrónica desde el año 1997 y Doctor en Ciencias Técnicas desde el año 2008. Posee la categoría científica de Investigador Titular desde el año 2012 y en 2018 recibió la Orden “Carlos J. Finlay” por los resultados alcanzados en la actividad científica. Labora en el Centro de Investigación y Desarrollo de Electrónica y Mecánica, “CID MECATRONICS” La Habana, Cuba. Correo electrónico: [e-mail], No. ORCID: 0000-0002-8884-320X. Sus principales intereses de investigación son las antenas de banda ancha y el diseño de arreglos de antenas.

Alexander Rogelio Ramírez Zaldívar, es ingeniero en Telecomunicaciones, graduado del ITM “José Martí” en el año 2015. Obtuvo el título académico de Máster en Sistemas Digitales en la Universidad Tecnológica de la Habana “José A. Echeverría” en el año 2023. En la actualidad opta por el grado científico de Doctor en Ciencias Técnicas en el ITM “José Martí”. Trabaja en el Centro de Investigación y Desarrollo de Electrónica y Mecánica, “CID MECATRONICS”, La Habana, Cuba. Correo electrónico: [e-mail], No. ORCID: 0000-0002-0372-0746. Sus principales intereses de investigación son el diseño de antenas y el procesamiento de señales.

Abel Hernández Violat, es Ingeniero Radioelectrónico, graduado en el ITM "José Martí" en el año 1994, posee la categoría científica de Investigador Auxiliar desde el año 2014. En la actualidad opta por el grado científico de Doctor en Ciencias Técnicas en el ITM “José Martí”. Trabaja en el Centro de Investigación y Desarrollo de Electrónica y Mecánica “CID MECATRONICS”, La Habana, Cuba. Correo electrónico: [e-mail], No. ORCID: 0000-0001-6886-3871. Sus principales intereses de investigación lo comprenden el procesamiento de señales y el diseño de receptores definidos por software en FPGA.