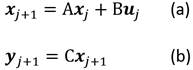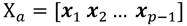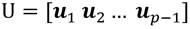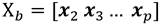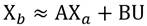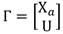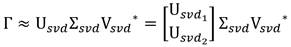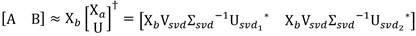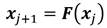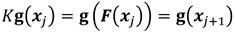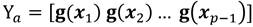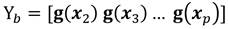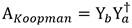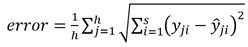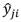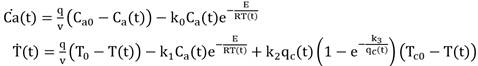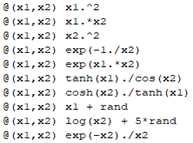Introducción
La Industria 4.0 es un paradigma que ha revolucionado la forma en que las empresas fabrican, mejoran y distribuyen sus productos. Algunas de las tecnologías que sirven como pilar para el desarrollo de la Industria 4.0 son el Internet Industrial de las Cosas (IIoT, por sus siglas en inglés), la Computación en la Nube, el Big Data, la Inteligencia Artificial y el Aprendizaje Automático. El objetivo en este caso es mejorar la productividad y la eficiencia mediante el uso de herramientas de monitoreo de condición [1, 2, 3]; la flexibilidad y la seguridad [4]; a la vez que se brinda la posibilidad de tomar decisiones y una personalización más inteligente en las operaciones de fabricación y de la cadena de suministro.
Los gemelos digitales son una tecnología clave en la Industria 4.0, por lo que ha habido cierto auge en su estudio [5, 6, 7, 8, 9]. Un gemelo digital, según [10], consiste en una representación de un objeto físico o proceso en un ambiente virtual. Los mismos se utilizan para modelar y simular procesos, sistemas y productos en tiempo real. En la Industria 4.0, los gemelos digitales se utilizan en una amplia gama de aplicaciones, desde el diseño hasta la planificación de la producción o la optimización de la cadena de suministro. Estos permiten la simulación y predicción del comportamiento de un objeto o proceso físico ante distintas circunstancias, lo que facilita la monitorización y gestión remotas, apoyo a labores de soporte y mantenimiento, la prevención de tiempos de inactividad, así como la personalización de la producción a los requerimientos del cliente.
Los gemelos digitales representan procesos dinámicos con una determinada relación entre sus variables de entrada y de salida. El contar con un modelo matemático que describa sus diferentes dinámicas es crucial para poder analizar, simular, predecir o controlar su comportamiento. Sin embargo, la obtención de este último no es algo trivial. En este sentido existen dos grandes grupos de métodos: los analíticos y los basados en datos. Los primeros se apoyan en el conocimiento previo de las leyes físicas que rigen el sistema y utilizan técnicas matemáticas para obtener un modelo que se ajuste a los datos observados. Los segundos, por el contrario, requieren ninguno o poco conocimiento a priori del sistema, y se apoyan en técnicas de aprendizaje automático o inteligencia artificial para extraer la información relevante de los datos y construir un modelo empírico. La identificación de sistemas, por su parte, puede verse en un punto medio, puesto que se puede usar el método analítico para obtener una estructura inicial del modelo y luego ajustar esta estructura con la información que se recoja a partir de datos experimentales.
En el contexto de la industria 4.0, donde los sistemas son cada vez más complejos y no lineales; la obtención de modelos a partir de los datos del proceso es una opción a tener en cuenta [11, 12, 13]. Por un lado, es flexible a los cambios del sistema; pues se puede actualizar el modelo automáticamente a partir de nuevos datos. Por otro lado, es eficiente, al permitir manejar grandes volúmenes de datos provenientes de múltiples sensores. Además de que son más rápidas y económicas, en el sentido de que la identificación ocurre al aplicar un algoritmo y no necesita la formulación de hipótesis o supuestos complicados sobre el comportamiento del proceso.
El operador de Koopman es una herramienta matemática que permite analizar sistemas dinámicos no lineales mediante una transformación lineal en un espacio de funciones (observadores). La teoría de Koopman plantea que es posible representar un sistema dinámico no lineal en términos de un operador lineal de dimensión infinita [14]. Algunos de sus campos de uso son: la robótica [15], el automovilismo [16] y el control de sistemas [17], entre otros.
Debido a que el operador de Koopman es infinito-dimensional, se han desarrollado técnicas que logran una representación reducida con la que es viable el desarrollo de aplicaciones prácticas. El análisis a partir de la Descomposición en Modos Dinámicos (DMD), está conectado con el operador de Koopman en este sentido [14]. Esto se debe a que DMD es una técnica que utiliza datos del proceso para obtener una aproximación lineal de las dinámicas de un sistema [18]. Existe una generalización de este algoritmo, llamada Descomposición en Modos Dinámicos con Control (DMD) que permite incluir en el análisis las señales de control [19]. Existe una segunda generalización, conocida como Descomposición en Modos Dinámicos Extendida (EDMD) propuesta por [20]. En este caso se busca encontrar el conjunto de autofunciones, autovectores y autovalores del operador de Koopman a partir de una aproximación finita del mismo; permitiendo con esto hallar la respuesta en el tiempo del sistema. Esto ha permitido ampliar grandemente el área de aplicación de esta técnica sin implicar un aumento apreciable en la complejidad del algoritmo. Los algoritmos basados en DMD han sido utilizados en diferentes tipos de aplicaciones: estudio de fluidos [21], estimación de parámetros de una aeronave [18], análisis de la temperatura en edificios inteligentes [22], entre otros.
Aunque se ha avanzado significativamente en la conexión de DMD con sistemas no lineales, la adecuada elección de los observadores de Koopman sigue siendo un reto. Esto se debe a que la mayoría de los trabajos se enfocan en diferentes formas de encontrar una aproximación del operador de Koopman y de acuerdo a esto seleccionan los observadores a partir de lo que pudiéramos identificar como conocimiento de experto [23, 24, 25, 26]. Sin embargo, esta investigación no sigue la tendencia de la mayoría de los investigadores asociada al uso de DMD y EDMD para la selección de los observadores [27, 28, 29, 30]. Alternativamente, se propone la aplicación de la teoría de Koopman asociada directamente con DMDc. De esta forma se tendrán las ventajas de analizar sistemas dinámicos no lineales y obtener las matrices A y B del modelo lineal en el espacio de estados; permitiendo con ello el empleo de diferentes tipos de técnicas de la literatura clásica que son ampliamente usadas para el análisis de sistemas y el diseño de controladores como en los enfoques presentados en [31] y [32] por solo citar dos ejemplos.
El objetivo fundamental de este trabajo y su principal contribución científica es la propuesta de un procedimiento para la selección del conjunto de observadores de Koopman resolviendo un problema de optimización. Como resultado de la aplicación del procedimiento se obtiene la cantidad mínima de observadores que minimizan el error entre las observaciones reales de un proceso y las obtenidas a partir del modelo lineal estimado para el desarrollo de un gemelo digital. Para resolver el problema de optimización se puede usar cualquiera de los muchos algoritmos de optimización que aparecen en la literatura. En este trabajo se utilizó un Algoritmo Genético (AG).
Para evaluar la efectividad del algoritmo propuesto se aplicó el mismo en la obtención del modelo de un Tanque de Reactor Continuamente Agitado (CSTR por sus siglas en inglés) obteniéndose resultados muy satisfactorios [33].
El trabajo está organizado de la siguiente forma: en la sección 2 se describen los elementos fundamentales de las herramientas utilizadas y el algoritmo propuesto; en la sección 3 se presenta el modelo del CSTR, el diseño del experimento para la prueba del algoritmo y el análisis de los resultados obtenidos. Finalmente se exponen las conclusiones.
Materiales y métodos
Descomposición en modos dinámicos con control
La descomposición en modos dinámicos es una técnica de análisis de datos que se utiliza para identificar sistemas dinámicos a partir de datos experimentales. La misma permite utilizar datos muestreados de elevada dimensionalidad de los procesos para extraer estructuras coherentes que contengan las características dominantes del comportamiento dinámico de estos últimos [34]. Estas estructuras, denominadas modos dinámicos, corresponden fuertemente a los autovectores del espacio de estados que gobiernan el sistema dinámico subyacente. Una vez obtenidos los modos dinámicos, se pueden utilizar para construir un modelo matemático lineal que describa el comportamiento dinámico del proceso bajo estudio.
La extensión de DMD que permite tener en cuenta señales de entrada (o de control) se denomina DMDc. La aplicación de este método necesita de tres elementos básicos:
p observaciones o mediciones del sistema objeto de estudio en diferentes instantes igualmente espaciados en el tiempo: x j ;
las señales de entrada al proceso en los mismos instantes que el vector de observaciones: u j ;
las observaciones del sistema avanzadas un instante de tiempo: x j+1 .
La idea es lograr identificar las matrices A y B que describen la dinámica del sistema según la siguiente relación Ecuación 1:
Donde A ∈ R n×n , B ∈ R n×m y C ∈ R s×n siendo n la dimensión del sistema, m la cantidad de entradas y s la cantidad de salidas. Por otro lado, y j+1 es el vector que representa las salidas del proceso.
Los datos del sistema pueden ser agrupados en las siguientes matrices, Ecuación 2, Ecuación 3, Ecuación 4:
de esta forma la Ecuación 1.a puede reescribirse como Ecuación 5:
En su caso más genérico DMDc se centra en encontrar la aproximación lineal que mejor ajusta a las matrices A y B. De forma resumida los pasos seguir son los siguientes [14]:
Crear la matriz de las entradas. Ecuación 6:
Realizar la descomposición en valores singulares de la matriz Γ. Ecuación 7:
Obtener las matrices A y B del sistema lineal. Ecuación 8
donde † es la pseudo-inversa Moore-Penrose.
La obtención de este modelo lineal en el espacio de estados permite aplicar diferentes tipos de técnicas de la literatura clásica que son ampliamente usadas para el análisis de sistemas y el diseño de controladores.
El operador de koopman
El operador de Koopman es otra herramienta de análisis que se utiliza para estudiar las propiedades de un sistema dinámico. Básicamente se reduce a que todo sistema no lineal puede ser aproximado a un sistema infinito-dimensional lineal [14]. Por supuesto, en la práctica es imposible trabajar con un sistema de dimensión infinita, por tanto, es necesario encontrar una aproximación de dicho operador.
Partiendo de que la evolución dinámica de un sistema discreto está dada por Ecuación 9:
la teoría de Koopman puede representarse de forma simplificada con la siguiente relación Ecuación 10:
Donde K es la aproximación del operador y g es un vector de funciones, también conocidos como observadores de los estados del sistema. La introducción de estos denominados observadores, a partir de un diccionario o biblioteca de funciones (D), es la que va a permitir captar aquellas no linealidades presentes en las dinámicas para lograr la aproximación lineal.
Para obtener el operador de Koopman en una dimensión finita basta seguir los siguientes pasos [14]:
De las matrices X a y X b formar Y a y Y b respectivamente Ecuación 11, Ecuación 12:
Aplicar DMD para obtener la aproximación del operador Ecuación 13:
Si se analizan con detenimiento las Ecuaciones (8) y (13) se aprecia que existe una estrecha relación entre DMDc y el operador de Koopman. Esto se debe a que la teoría detrás de DMD puede ser considerada una aproximación numérica del análisis espectral de Koopman, lo que permite su aplicación a sistemas dinámicos no lineales [35].
Algoritmo genético
Los Algoritmos Genéticos son algoritmos de optimización estocástica inspirados en los principios de la evolución y la selección natural [36, 37, 38]. De forma resumida, un AG se encarga de evolucionar una población compuesta por diferentes individuos hacia el individuo o solución óptima [39].
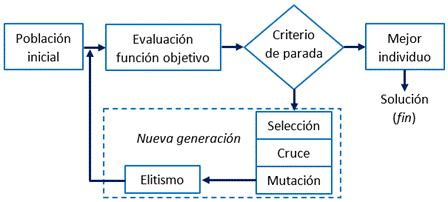
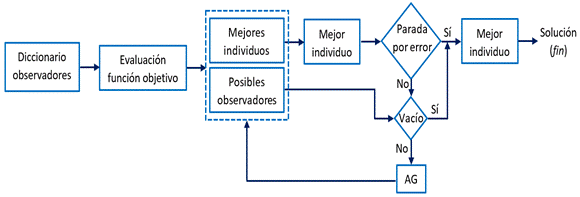
El procedimiento elemental seguido por un AG mono-objetivo se representa esquemáticamente en la Fig. 1. El mismo comienza con la denominada población inicial, que consiste en un conjunto de N individuos que suelen ser generados aleatoriamente. A cada individuo se le calcula su valor de adaptación haciendo uso de la función objetivo. Luego se investiga si alguno de los individuos cumple con el requisito de optimización buscado; por ejemplo, el error mínimo permitido. En caso de que al menos uno de los individuos cumpla con este criterio de parada, se selecciona al mejor individuo como resultado final del algoritmo. En caso de no ser así, se pasa a crear una nueva generación (también de tamaño N), la cual constituirá la nueva generación. Para esto se aplican mecanismos de selección, cruce, mutación y, en algunos casos, elitismo. Una vez creada la nueva generación, esta pasa a ser la nueva población y el algoritmo vuelve al punto de evaluar la función objetivo. Este proceso se repetirá una y otra vez hasta que se logre el criterio de parada antes mencionado, o hasta que se cumpla una cantidad predefinida de iteraciones.
Metodología para la selección óptima de observadores
Algunas consideraciones
Como se ha mencionado anteriormente, la idea es contar con un algoritmo que, sin tener conocimiento previo del sistema y usando datos del mismo, permita la selección automática del menor conjunto de observadores de Koopman que minimizan el error entre el proceso real y el modelo lineal que se obtiene con la aplicación de DMDc. Es importante resaltar que: i) estos observadores serán escogidos a partir un diccionario de funciones de observación D previamente construido y ii) que el diccionario debe ser lo suficientemente amplio para abarcar diferentes tipos de no linealidades. Partiendo de lo anterior, se plantea un problema de optimización que utilizará como herramienta un algoritmo genético mono-objetivo cuyas características fundamentales se presentan a continuación:
Cada población en el AG estará compuesta por z individuos, los cuales consisten en arreglos de etiquetas. Cada etiqueta será un número entero y representará la posición de un observador en el diccionario definido. Por ejemplo: dado el diccionario
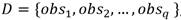 , un individuo compuesto por los dos primeros observadores tendría la siguiente codificación:
, un individuo compuesto por los dos primeros observadores tendría la siguiente codificación:  .
.Como no se tiene conocimiento previo de la cantidad de observadores que serán necesarios, el AG será aplicado para diferentes tamaños de individuo (l). Dado un diccionario de q observadores, el intervalo de tamaños de individuo permitido queda en el rango:
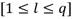 .
.Si bien el resultado de DMDc son las matrices A y B de un modelo con dimensión mayor a la del sistema original (debido a la aplicación de la teoría de Koopman); las salidas finales del modelo serán las estimaciones de las salidas de la Ecuación 1.b:
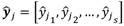 .
.La función objetivo para el proceso de optimización será la media del error entre las muestras originales
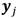 y las salidas del modelo estimado
y las salidas del modelo estimado 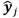 . El cual se define como (14):
. El cual se define como (14):
donde:
h |
es el número total de muestras. |
s |
es el número total de salidas del sistema. |
yji |
es el valor real del i-ésimo elemento de salida de la j-ésima muestra. |
es el valor estimado del i-ésimo elemento de salida de la j-ésima muestra. |
Al hacer uso de la distancia se garantiza que, sin importar la dimensionalidad del sistema, siempre se podrá emplear un AG mono-objetivo. En este caso se usó la distancia euclídea.
Se tendrán dos criterios de parada:
El primero es el error máximo permitido, que se asocia al valor de adaptación calculado por la función objetivo.
El segundo es que no existan más posibles combinaciones a evaluar por el AG.
Los mecanismos para crear la nueva generación en el AG son: selección por torneo binario y mutación puntual. Además, también se empleará elitismo para asegurar que las mejores soluciones sean las que pasen a la siguiente población.
El operador genético de cruce no fue empleado, pues sólo se podrían intercambiar los últimos observadores de cada combinación y, por tanto, los hijos resultantes serían iguales a sus padres.
Algoritmo propuesto
El algoritmo empieza evaluando cada observador del diccionario de funciones para escoger al mejor individuo (aquel que produce el menor valor de la función objetivo - error). Además de este individuo, también se guardarán aquellos que devuelvan un valor de adaptación hasta un 10% mayor que el menor obtenido, constituyendo con esto el conjunto de mejores individuos. De esta forma se evita caer en un mínimo local, pues se da la oportunidad de probar otras combinaciones de funciones.
A continuación, corresponde buscar las mejores combinaciones de dos observadores. Para ello se crea un conjunto de posibles observadores que en esta etapa inicial estará formado por todos los observadores del diccionario. Con esto se permite probar cada uno de estos últimos con los mejores individuos ya seleccionados de un observador. El AG será el encargado de lograr la combinación de observadores que minimiza el error, devolviendo un nuevo conjunto de mejores individuos, donde el tamaño de cada elemento se habrá incrementado en uno respecto a sus predecesores. El elemento final de cada individuo de este último conjunto será guardado para formar la nueva lista de posibles observadores, pues son las funciones que el AG detectó que sí contribuyen a una disminución significativa del valor de adaptación.
El AG será aplicado repetidamente en cada actualización de mejores individuos y posibles observadores hasta que ya no queden combinaciones por analizar. Además, hay que resaltar que cuando se terminen de probar las combinaciones para cada individuo en mejores individuos, se analizará si algún resultado devolvió un error estrictamente menor que el mejor individuo para así actualizar el que será la solución final del método que es el conjunto menor de observadores con el que se obtiene el menor error.
La Fig. 2 muestra un diagrama con la lógica propuesta.
Diseño de experimentos y análisis de los resultados
Tanque reactor continuamente agitado
Un proceso que ha sido bastante estudiado en la literatura es el caso del CSTR. El modelo, recogido en [33] se presenta a continuación (15):
Las variables de mayor interés son:
x1 = Ca(t) |
concentración del componente A (mol/l) - variable de estado 1. |
x2 = T(t) |
temperatura de la mezcla (K) - variable de estado 2. |
u = qc(t) |
flujo del refrigerante (l/min) - señal de control. |
La base de datos utilizada cuenta con un total de 7500 muestras, tomadas a intervalos de 6 segundos.
Diseño de experimentos
El objetivo de este experimento es obtener, de forma automática, el menor conjunto de observadores de Koopman que aplicados a DMDc producen el mejor modelo lineal del proceso estudiado.
Teniendo esto en cuenta, se definió el diccionario de observadores formado por las 10 funciones que aparece en la Fig. 3. Este diccionario fue construido específicamente para el presente experimento, pero la variedad y cantidad de no linealidades puede variar según decidan los especialistas que usen el presente procedimiento. Por otra parte, se debe mencionar que de las 7500 muestras presentes en la base de datos se tomaron 6000 para la estimación del modelo y el resto para la validación. El criterio de parada por error fue establecido en 0.05. Para asegurar la validez del experimento desde el punto de vista estadístico el mismo se repitió 50 veces.
El experimento se realizó en una computadora con las siguientes características: procesador Intel(R) Core(TM) i7-7500U CPU @ 2.70GHz 2.90 GHz; 8GB de RAM y Sistema Operativo “Windows 10 Pro for Workstations” versión 22H2. El software utilizado fue MATLAB R2019b y no se empleó ninguna librería externa ni especializada del propio software.
Análisis de los resultados
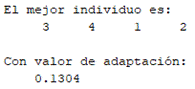
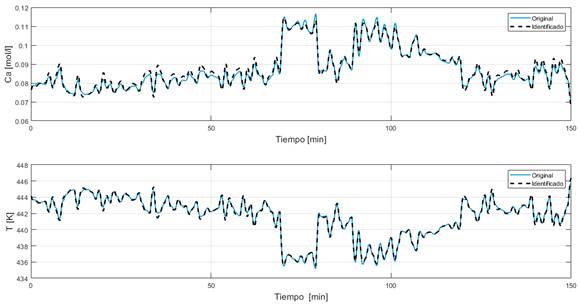
Luego de realizar los experimentos se tuvo que la solución final es el individuo formado por los 4 primeros observadores del diccionario (Fig. 4). Un aspecto a señalar es que en ninguno de los casos se logró el valor de error deseado y que, por tanto, cada parada del AG fue por haberse agotado la cantidad de combinaciones de observadores.
El tiempo medio de ejecución de los experimentos fue de 0.22 segundos. Como se aprecia, este tiempo medio de ejecución no resulta elevado, pues es un experimento que no se repite continuamente y que no interviene en el funcionamiento normal del proceso bajo estudio. Ello implica que el sistema físico no se verá afectado en ninguna medida por estas demoras. No obstante, hay que tener en cuenta que aspectos como la cantidad de muestras del proceso y el tamaño del diccionario de funciones tiene una influencia directa en estos tiempos.
La Fig. 5 muestra las matrices A y B de la aproximación lineal del sistema, así como la matriz de los autovalores (Σ), cuando se aplicó el algoritmo DMDc al individuo final.
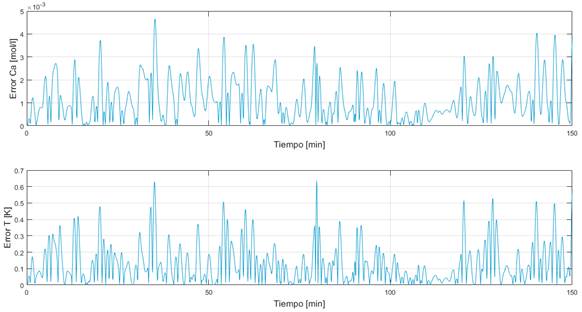
Por otro lado, en la Fig. 6 se aprecia la distancia euclídea (error) para cada muestra de validación. Además, la Fig. 7 y la Fig. 8 presentan los resultados de la simulación para el conjunto de datos de validación; donde se aprecia que el modelo final resulta adecuado para el sistema bajo estudio. La primera figura presenta la comparación de los datos reales con los simulados a partir de las matrices A y B. La segunda figura muestra los errores en el tiempo de cada variable de estado.
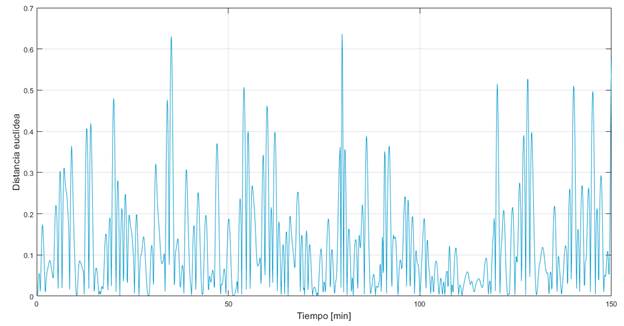
Figura 6 Error (distancia euclídea) entre los pares 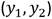 y
y 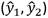 para cada observación del conjunto de validación.
para cada observación del conjunto de validación.
Conclusiones
En este trabajo se propuso y se demostró la validez de un algoritmo para la selección óptima de observadores de Koopman aplicados a DMDc en la obtención de gemelos digitales. Al usar DMDc se pudieron obtener, a partir de las observaciones del proceso, las matrices A y B del sistema lineal discreto en el espacio de estados, brindando así la posibilidad de aplicar diferentes técnicas de análisis sobre el gemelo digital. Por otro lado, con base en la teoría de Koopman, se utilizaron observadores para lograr identificar las dinámicas no lineales del proceso. De este último resalta que la selección adecuada de dichos observadores es un paso crítico que afecta directamente la eficacia del método en la descripción y análisis de los sistemas dinámicos no lineales. Por tanto, con la propuesta de algoritmo a partir del planteamiento de un problema de optimización basado en AG, se garantiza que se prueben las mejores combinaciones de observadores para el sistema bajo estudio. Así, el usuario del método podrá prescindir de la necesidad de conocimiento de experto sobre las posibles dinámicas que tienen lugar en el sistema. Sin embargo, un importante aspecto a tener en cuenta, es que se debe contar con un diccionario de observadores lo suficientemente amplio para abarcar diferentes tipos de no linealidades.
Otro factor al que hay que prestarle atención es la cantidad y la calidad de las muestras utilizadas, pues las mismas deben cubrir un rango adecuado de condiciones de operación, garantizando con esto que el algoritmo pueda detectar las dinámicas fundamentales del proceso.