Original Article

Optimization of pipe networks by genetic algorithm employing the colebrook correlation

Optimización de redes de tuberías por algoritmo genético que emplea la correlación de colebrook

Ricardo de Souza-Antunes^{I  *}  , Felipe dos Santos-Loureiro, Luís Antônio-Scola^I  , João Flávio Vieira-de-Vasconcellos^II 

^I. Federal University of São João del-Rei, Thermal Sciences and Fluids Department. Minas Gerais, Brasil

^II. State University of Rio de Janeiro, Polytechnic Institute, Mechanical and Energy Department. Rio de Janeiro, Brasil

Abstract

This paper presents an optimization procedure for identifying the minimum cost of water pipe networks considering a table of commercial diameters. To this end, a real-coding Genetic Algorithm (GA) with the use of a simulated binary and convex crossover and mutation per variable; as well as a dynamic penalty strategywasdeveloped. A computer program to solve the hydraulic model based on the Newton-Raphson method wasdevelopedfor calculating the head loss using Hazen-Williams (HW) and Colebrook correlations. By analyzing a benchmark pipe network example, it is shown that different results are obtained by the HW and Colebrook correlations. Moreover, when simulating the best HW pipe network configuration with the Colebrook correlation, some constraints of the design are violated, indicating that the Colebrook formulation is more adequate to be used in conjunction with the GA due to the randomness of the GA with respect to the Reynolds numbers.

Key words: pipe networks; hazen-Williams; colebrook; optimization; genetic algorithm

Resumen

Este artículo presentó un procedimiento para identificar el costo mínimo de redes de tuberías para agua considerando los diámetros comerciales diponibles. Para esto, fue desarrollado un Algoritmo Genético (AG) de codificación real con el uso de un cruzamiento binario simulado y convexo, mutación por variable y penalización dinámica. El método de Newton-Raphson es utilizado para calcular las pérdidas de carga empleando las correlaciónes de Hazen-Williams (HW) y Colebrook. Analisando una red de tuberías benchmark, es posible observar que los resultados obtenidos mediante el uso de las correlaciones de HW y Colebrook son diferentes. Además, al simular la mejor configuración de red de tuberías de HW con la correlación de Colebrook, se observa que algunas restricciones del diseño son violadas, lo que indica que la formulación de Colebrook es más adecuada para ser utilizada junto con la AG debido a la aleatoriedad del AG con respecto a los números de Reynolds.

Palabras-clave: redes de tuberías; hazen-williams; colebrook; optimización; algoritmo genético

Introduction

Internal flows in pipe networks appear in various parts of today’s industrialized society. From the supply of potable water ^[1,2] to the transportation of chemicals and other industrial fluids ^[3,4], engineers have designed and built countless miles of piping systems ^[5]. In the design process of pipe networks, engineers must ensure that the design criteria (e.g., flow rates in the pipes and heads on the nodes) are satisfied with a minimum cost in terms of material, installation, etc. This optimum design of pipe networks can be addressed by optimization techniques.In fact, such an approach has been employed for designing water distribution systems since 1970’s ^[6]. In what concerns the optimization methods, stochastic methods such as Genetic Algorithmsare widely adopted rather than classical deterministic ones. This stems from the difficulty of deterministic methods in working with commercial diameters which are not continuous functions ^[6]. The primary requirement or objective in a pipe network design is the cost associated with the chosen commercial diameters. According to ^[7], this cost is responsible for approximately 70% of the total cost of the network ^[8].

The methods for solving the flow equations in pipe networks required in the optimization process are not trivial in their majority and not unique because nonlinear equations are always present in the model of hydraulic systems. Generally, two methods, namely, Hardy Cross ^[3,4,9] and Newton-Raphson are widely employed ^[2]; besides, they can be classified as indirect or direct.The indirect Hardy Cross methodrequires a set of interior loops and its application to large pipe networks is quite cumbersome. On the other hand, the application of theNewton-Raphsonis straightforward since onlynodal equations are required. Finally, a proper manipulation of the nonlinear equations gives rise to a finite element based method in which element matrices concerning the pipes are assembled to yield the final system of nonlinear equations. Differently from the Newton-Raphson method, in the finite element based method the time required for preparing input data is much reduced ^[10,11].

In the hydraulic model, it is important to define a correlationthat accounts for the frictional energy loss.The Hazen-Williams (HW) and Colebrook are the mostcommon correlations. The former is widely used in articlesbased on optimization procedures ^{[1,2,6,12,13,14,15]} due to its easy computational implementation, while the latter is more general but requires a solution of a nonlinear equation and, therefore, not widely employed in such a context.Moreover, due to the great randomness of GA, a wide range of Reynolds numbers is likely to be explored, leading to a non-recommendation of strict use of the HW correlation.Bearing in mind this fact, the present workpresents a comparison between the HW and Colebrook correlations when applied tothe optimization of pipe networks by the GA, discussing the importance of selecting appropriate correlations in order to yield meaningful results generated by the GA.Furthermore, the developed GA based program is characterized by the implementation of a mixed crossover operator, mutation per variable and a dynamic penalty strategy. The first incorporates the characteristics of both the convex and simulated binary crossovers, the second allows to keepthe information part of the individual, while the third aims at gradually increasing the penalty factor of infeasible individuals during the generations and, therefore, avoiding a premature convergence of the algorithm.

To execute this research work will be necessary sensitivity tests involve the parameters, population size, generation number, crossover and mutation probabilities, elitism, extrapolation size in crossover, polarization probability, penalty factor. After to define the best parameters, the optimizations will be performed with both correlations, HW and Colebrook, and the optimal solution obtained by HW correlation will be simulated with Colebrook correlation.

Finally, the analysis of the results leads to the conclusion that due to the large variation of the Reynolds number during the optimization process, the correlation of Colebrook, despite the increase in cost in the network, is more appropriate than HW, since, this is accurate only for a small range of the Reynolds number.

Methods and Materials

To evaluation of the problem has been proposed, this section will present the approaches used along with their respective mathematical modeling. First,Hydraulic model,the equations of conservation of energy and mass will be presented, addressing mainly the method for calculating the head losses and the Newton-Raphson method, such method is chosen, mainly, due to linearity of the energy equations. Second, will bepresentedthe optimization model and the method that will be used for resolution, in this case the genetic algorithm. Finally, the two source pipe network will be introduced with the respective data required to solve the problem.

Hydraulic Model

Let $V=\left\{I:I\in {\mathbb{Z}}^{+}\mathrm{,1}\le I\le M\right\}$ be the set of pipes in the network and $S=\left\{i:i\in {\mathbb{Z}}^{+}\mathrm{,1}\le i\le N\right\}$ be the set of nodes that connects the pipes. When the energy conservation is applied along with each pipe of length from node $i$ to node $j$ , the following expression arises owing to the energy transformation caused by the friction in real flows, equation (1)

$H_i=H_j+h_I,\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\forall I\in V$ (1)

where $H_i$ stand for energies(heads) in the nodes and $h_I$ are frictional energy losses(or head losses) along the pipes which can be defined as ^[3], equation (2)

$h_I=R_I{Q}_I{}^{\beta };R_I=\frac{8f_I{\text{L}}_I}{g{\pi }^2{D}_I^5}$ (2)

where $R_I$ are the so-called hydraulic resistances of Darcy-Weisbach (DW), $Q_I$ arevolume flow rates with $\beta$ being a given exponent (generally $\beta =2.0$ ), $f_I$ are friction factors, $g$ is gravitational acceleration, ${\text{L}}_I$ and $D_I$ are, respectively, lengths and diameters of the pipes.

The friction factorsfor the turbulent flow can be determined by the Colebrook equation ^[16] defined as, equation (3)

$\frac{1}{\sqrt{f_I}}=-2.0{\log }_{10}\left(\frac{e_I}{3.7D_I}+\frac{\mathrm{2,51}}{{\mathrm{Re}}_I\sqrt{f_I}}\right)$ (3)

where ${\mathrm{Re}}_I$ are Reynolds numbers and $e_I$ are absolute roughnesses concerning the pipes. On the other hand, if the flow is laminar, the friction factors arereadily computed as $f_I=64/{\mathrm{Re}}_I$ .

In order to simplify the calculation of the hydraulic resistances, Hazen-Williams ^[17] proposed an alternative expression that is not directly dependent on the friction factor, i.e. equation (4)

$R_I=\frac{K_1{\text{L}}_I}{C_{\text{HW}}^{\beta }{D}_I^m}$ (4)

where the valuesof $K_1,\beta \text{and}m$ are, respectively, 10.68, 1.85, 4.87 and $C_{\text{HW}}$ is the HW coefficient.

Under the assumptions of the same head lossand water at 20ºC, equations and can be manipulated in order to yield the following equivalent friction factors for the HW ^[5], equation (5)

$f_I=\frac{1056}{C_{\text{HW}}^{1.85}{D}_I^{0.02}{\mathrm{Re}}_I^{0.15}}$ (5)

Figure 1 shows the difference between equations and considering different values for the diameters(such a range of diameters will be employed in the results section). Analyzing the figure, one can conclude thatthe calculation of the head losses using the HW is only accurate for a limited range of Reynolds numbers; even though, it is quite common to find several published articles that adopt the HW.

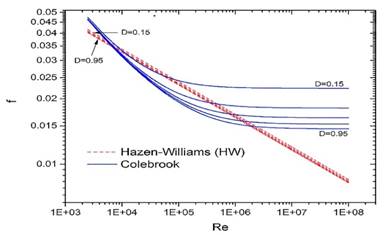
Fig. 1 Friction factor comparison between the Colebrook equation with $e=0.00025$ m and HW with $C_{\text{HW}}=130$  

In addition to the energy equation, the mass conservation must be employed in each node. For incompressible and steady flow, uniform velocity and non-deformable control volume, one obtains equation (6)

${\displaystyle \sum _{I\in {\tilde{V}}_i}\left(Q_I^{out}-Q_I^{in}\right)}+Q_i^e=\mathrm{0,}\forall i\in S$ (6)

where $Q_i^e$ are known demands on the nodes and ${\tilde{V}}_i$ are subsets of $V$ formed by the pipes that intercept the node $i$ .

Finally, let $H\in {ℝ}^N$ , $Q\in {ℝ}^M$ be, respectively, the energy and flow rate vectors and let $x={\left[\begin{array}{cc}H& Q\end{array}\right]}^T$ be the augmented vector. After applying equations and to all the pipes in the network, a nonlinear system of equations,concisely written as $f\left(x\right)=r$ ,is obtained in which $r\in {ℝ}^{N+M}$ stands for a known vector formed by the prescribed flow rate demands on the nodes as well asrelative altitudes of the pipes. Since the system is nonlinear, the Newton Raphson method is employed for solving the hydraulic equations, yielding equation (7)

$\begin{array}{l}{J}_{ij}\left(x_k\right)\Delta x_{k+1}=r-f\left(x_k\right)\\ x_{k+1}=x_k+\Delta x_{k+1}\end{array}$ (7)

where $J_{ij}\left(x_k\right)=\frac{\partial f_i\left(x_k\right)}{\partial x_j}$ is the Jacobian matrix.

Optimization Model

Let $B=\left\{D_c:D_c\in {ℝ}^{+}\mathrm{,1}\le c\le A\right\}$ be the set of commercial diameters and let $\text{C}(D_c)$ be the pipe cost per unit length associated with each diameter. A pipe network must be designed with a minimum cost owing to this set of diameters such that the constraints are fulfilled. Thus, the mathematical formulation for the optimization of pipe networks can be expressed as follows, equation (8)

$\begin{array}{l}{D}^{*}=\arg \min F(D)\\ \text{s}\text{.t}{\text{.: g}}_i(D)\le \mathrm{0,}\forall i\in S\end{array}$ (8)

where $D\in {ℝ}^M$ is the diameter vector concerning the networkformed by the commercial diameters (i.e., $D_I\in B$ ) and $F\left(D\right)={\displaystyle \sum _{I=1}^M{\text{L}}_I\text{C}(D_I)}$ is the objective function to be minimized, $D_{}^{*}$ is the diameter vector which minimizes the objective function subject to the constraints of inequality $g_i\left(D\right)=H_i-H_i^{\min }$ with $H_i^{\min }$ being the minimum heads requiredfor the nodes.In order to handle these constraints, a procedure of dynamic penalizationhas been employed, this transformthe constrained optimization problem into a non-constrained optimization problem ^[18]. The formulation problem is express as follows, equation (9)

$\begin{array}{l}{D}^{*}=\text{arg min}\left(F\left(D\right)+P\left(D\right)\right)\\ P\left(D\right)=p\left({\displaystyle \sum _{i=1}^N\max \left[-g_i\left(D\right)\mathrm{,0}\right]}\right)\text{,}p=\phi {\left(\frac{n_{ger}}{n_{ger\max }}\right)}^k\end{array}$ (9)

where $P\left(D\right)$ is zero for feasible solutions, $\phi$ is the penalty factor, $n_{ger}$ is the current generation, $n_{ger\text{max}}$ is the maximum number of generations and $k$ is an empiric constant which is set to $\mathrm{0,8}$ ^[14]. Moreover, the function $p$ is called dynamic penaltysince the selective pressure increases over generations.

To perform the optimization, a computational implementation based on real-coding Genetic Algorithmhas been employed. Theadopted crossover operator is based on a combination of simulated binary and convex crossovers;in the latter, individuals can be extrapolated following this equation $x_g=\alpha x_1+\left(1-\alpha \right)x_2$ according to the value of $\alpha \in [-{\alpha }_0\mathrm{,1}+{\alpha }_0]$ , where ${\alpha }_0$ is the maximum extrapolation value, $x_g$ is the new individual generated from the selected individuals $x_1$ and $x_2$ , or $\alpha =1.4{\beta }_1{\beta }_2-0.2$ , where ${\beta }_1$ and ${\beta }_2$ is chosen randomly and independently, with uniform probability distribution in the interval [0, 1] and probability of this $\alpha$ is chosen is pre-determined by polarization probability (pp) ^[19]. Each pair of parents generates a pair of children and pp is applied only in one child. The Gaussian mutation operator has been applied; and as observed in preliminary studies, mutation by variables rather than individuals achieved better performance ^[20]. The use of such reproduction operators improved both the objective function value and the number of the optimum points achieved in a group of executions. In addition, an elitism strategyhas beenalso employed to improve convergence.

Finally, it is necessary to couple the hydraulic and optimization models asillustrated inthe below flowchart, figure 2. The first step is to generate a random initial population with the diameters of the pipe networkas variables. With the diameter vector, the hydraulic simulation is performedto calculate the flow rates inthe pipes and loads in the nodes. Then, the fitness function is evaluated,and the constraints ${\text{g}}_i(D)\le 0$ are verified, penalizing only individuals that violate the constraints (infeasible solutions). Afterwards, selection of the induviduals for reproduction occurs to generate a new population. This process of selection, reproduction and fitness evaluationis repeated until the maximum number of generations is reached.

Fig. 2 Flowchart of the Genetic Algorithm coupled with the Hydraulic Model 

Two Source Problem

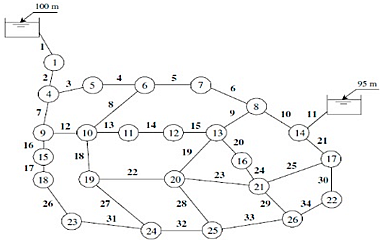
The pipe network analyzed inthis workis called Two-Source, and it is consisted of 34 pipes, 26 nodes and two water reservoirswith elevations(altitutes) of 95 and 100 m asdepicted in figure 3. The HW coeficient $\left(C_{\text{HW}}\right)$ is set to 130 and the associated roughness in the Colebrook correlation is assumed to be 0.25mm or 0.50mm considering cast iron ^[21]. Nodal demands $\left(Q_i^e\right)$ , minimun nodal heads ( $H_i^{\min }$ ) andpipe lengths $\left(L\right)$ are presented in table 1,while diameters with associated costs to be considered in the network design arein table 2.

Fig. 3 Illustration of the Two-Source pipe Network, adapted from^[13] 

Table 1 Nodal and Pipe Data for the Two-Source Network 

N (i)	Q i ^e (m ^3/s)	H i ^min (m)	N (i)	Q i ^e (m ^3/s)	H i ^min (m)	Pipe (I)	L (m)	Pipe (I)	L (m)	Pipe (I)	L (m)
1		100	14	10.6	82	1	300	14	500	27	900
2		95	15	10.5	85	2	820	15	1,960	28	650
3	18.4	85	16	9.0	82	3	940	16	900	29	1,540
4	4.5	85	17	6.8	82	4	730	17	850	30	730
5	6.5	85	18	3.4	85	5	1,620	18	650	31	1,170
6	4.2	85	19	4.6	82	6	600	19	760	32	1,650
7	3.1	82	20	10.6	82	7	800	20	110	33	1,320
8	6.2	82	21	12.6	82	8	1,400	21	660	34	3,250
9	8.5	85	22	5.4	80	9	1,175	22	1,170
10	11.5	85	23	2.0	82	10	750	23	980
11	8.2	85	24	4.5	80	11	210	24	670
12	13.6	85	25	3.5	80	12	700	25	1,080
13	14.8	82	26	2.2	80	13	310	26	750

Table 2 Commercial Diameters in mm andCost in rupees perlength 

Number	1	2	3	4	5	6	7
$D_c$	150	200	250	300	350	400	450
Cost	1,115	1,600	2,154	2,780	3,475	4,255	5,172
Number	8	9	10	11	12	13	14
$D_c$	500	600	700	750	800	900	1.000
Cost	6,092	8,189	10,670	11,874	13,261	16,151	19,395

Results and Discussion

In the stochastic optimization, a sensitivity analysis of the parameters must be performed because of the randomness of the variables. The parameters involved in the GA are the population size (Pop), number of generations ( $n_{ger\max }$ ), probability of crossover (Cross) and mutation (Mut), percentage of extrapolation in the crossover ( ${\alpha }_0$ ), elitism (e), polarization probability (pp) and penalty factor $(\phi )$ .

The following value ranges for the parameters were tested in the developed GA program: $\text{Pop}\in \left[\mathrm{1000,1300}\right]$ , $n_{ger\max }\in \left[\mathrm{700,850}\right]$ , $\text{Cross}\in \left[80\%;95\%\right]$ , $\text{Mut}\in \left[\mathrm{0.04,0.055}\right]$ , ${\text{α}}_0\in \left[\mathrm{0.1,0.5}\right]$ , $\text{e}\in \left[\mathrm{12,24}\right]$ , $pp\in \left[10\%;40\%\right]$ and $\phi \in \left[\mathrm{4.5,10.5}\right]$ , leading to the conclusion that the Pop, $n_{ger\max }$ , Cross, Mut and ${\alpha }_0$ parameters had a small influence on the results. As a result, $\text{Pop =1000}$ , $n_{ger\max }=800$ , $\text{Cross = 95\%}$ , $\text{Mut = 5\%}$ and ${\alpha }_0=0.3$ are adopted hereafter.

Finally, a statistical analysisis also performed, considering 11 independent runs of the GA and based on four sets of parameters as shown in table 3. These sets are classified as follows: (I) standard set of parameters, (II) set of parameters that resulted in the lowest found fitness function using the HW correlation, (III) set of parameters that presented a lower meanin the sensitivity analysis and with the use of the HW correlation, and (IV) same parameters adopted in (III) but with the Colebrook correlation.The minimum cost of the network, mean (both in thousands) and standard deviation (STD) are also presented in this table, whereas the optimum commercial diametersfor these four sets are displayed in table 4.

Table 3 GA parametersand results 

	Pop	n germax	Cross	Mut	α0	e	pp	φ	Minimum	Mean	Sth
I	1000	800	95 %	5 %	0.3	16	30 %	6.5	1,261.33	1,263.15	312,367
II	1000	800	95 %	5 %	0.3	24	30 %	6.5	1,253.11	1,263.15	438,346
III	1000	800	95 %	5 %	0.3	24	10 %	7.5	1,255.13	1,263.66	520,771
IV	1000	800	95 %	5 %	0.3	24	10 %	7.5	1,348.82	1,368.00	1,098,907

Table 4 Optimized diameters for the pipes 

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
I	900	900	350	300	150	250	800	150	600	600	800	750	500	450	150	500	350
	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34
	350	450	150	600	150	200	350	600	250	300	300	200	300	150	150	150	150
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
II	900	900	350	300	150	250	800	150	450	500	800	700	500	500	150	500	350
	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34
	400	150	150	700	150	450	350	700	250	250	300	200	300	150	150	150	150
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
III	900	900	350	300	150	250	800	150	450	500	800	700	500	500	150	500	350
	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34
	400	150	150	700	150	450	350	700	250	250	300	200	300	150	150	150	150
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
IV	900	900	400	300	150	250	900	150	450	600	900	750	500	500	150	500	400
	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34
	400	150	150	700	150	500	400	700	250	300	300	250	300	150	150	150	150

Concerning the set of parameters (II), a minimum cost of 125,311,060 rupees has been found, which is better than that found by ^[9], which is 125,501,130 rupees. On the other hand, it is observed that the minimum cost found with the Colebrook correlation, i.e. 134,882,470 rupees, set of parameters (IV), is greater than 125,513,720 rupees. Because of this result, a simulation with the Colebrook correlation considering the optimum network employing the HW correlation has been performed to verify if the constraints were indeed satisfied. The simulation results are presented in table 5 for roughness equal to 0.25 and 0.50 mm. It is worth noting that some head constraints are violated, indicating that the diameters are actually underestimated.

Table 5 Nodal head values considering the Colebrook correlation for the optimum HW network. The highlighted values represent a violation of the constraints 

Head (m)	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10	H11	H12
Colebrook 0.25 mm	98.3	95.2	85.0	82.3	82.7	87.3	91.3	88.3	86.1	84.5	80.6	93.5
	H13	H14	H15	H16	H17	H18	H19	H20	H21	H22	H23	H24
	87.5	80.4	89.8	84.0	85.5	80.8	86.3	83.4	80.4	76.1	77.8	76.0
	H1	H2	H3	H4	H5	H6	H7	H8	H9	H10	H11	H12
Colebrook 0.50 mm	98.1	94.5	82.7	79.7	80.5	86.0	90.0	86.6	84.0	82.2	78.3	93.2
	H13	H14	H15	H16	H17	H18	H19	H20	H21	H22	H23	H24
	85.7	78.0	89.0	81.6	83.4	78.5	84.9	81.5	77.4	72.6	75.1	73.0

This occurs because in the optimization process, the Reynolds number varies from $1.40x{10}^{-3}$ to $\text{2}\text{.59}x{\text{10}}^7$ as depicted in figure 4-b for the HW correlation, figure 4-a shows the evolution of the fitness function to the best value found. Hence, once the HW correlation is accurate only to a specific range of Reynolds number as shown in figure 1, its use in conjunction with the GA generates individuals with small errors in the hydraulic results that propagate during the GA generations.

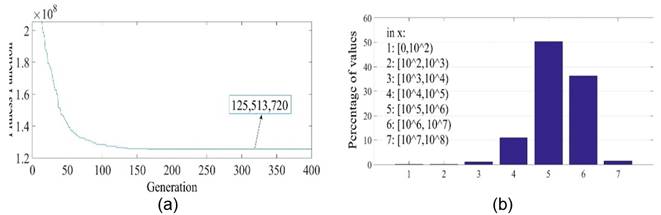
Fig. 4 Results for HW: (a) Convergence of the fitness function (Left), (b) Percentage of Reynolds ranges for all generations (Right) 

Thus, in an optimization process via GA, the Colebrook correlation should be used due to its high accuracy in calculating the hydraulic results for all Reynolds numbers. In this sense, the minimum cost of 134,882,470 rupees using the Colebrook correlation is justified by the fact that the some diameters need to be larger in order to guarantee the minimum heads in the nodes, see table 4.

Conclusions

Due to the great variation of the Reynolds number during the optimization process,it has been evident that the HW correlationis not appropriate since its use is accurate only for a small range of Reynolds number. This fact may lead to an optimum or good network configuration that is not the same when the Colebrook correlation, which is valid for all the range of Reynolds number, is employed, generating misleading results. In fact, it has been verified through an example that taking into account the optimumpipe network generated using the HW correlation, some of the heads in the nodes are underestimated when such a network is simulated employing the Colebrook correlation. Thus, it is concluded that when performing the optimization process with the Colebrook correlation, the diameters of the network are enlarged in order to satisfy the constraints, increasing the total cost of the network.

Acknowledgments

This work was partially supported by Universidade Federal de São João del Rei, Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).

References

1.  Jovic, V. Analysis and modelling of non-steady flow in pipe and channel networks. Applied Mathematical Modelling. 2016;40(2):966-83.

2.  Ates, S. Hydraulic modelling of closed pipes in loop equations of water distribution networks. Applied Mathematical Modelling. 2016;40(2):966-83.

3.  Brkic, D. An improvement of Hardy Cross method applied on looped spatial natural gas distribution networks. Applied energy. 2009;86(7-8):1290-1300.

4.  Martinez Benet M, Puigjaner L. A powerful improvement on the methodology for solving large-scale pipeline networks. Computers & chemical engineering. 1988;12(2-3):261-65.

5.  Potter MC, Wiggert DC. Fluid Mechanics. Fifth ed. USA: Cengage Learning Engineering; 2016.

6.  Suribabu CR. Heuristic-Based Pipe Dimensioning Model for Water Distribution Networks. Journal of Pipeline Systems Engineering and Practice. 2012;3(4):115-124.

7.  Dandy GC, Engelhardt MO. Multi-objective trade-offs between cost and reliability in the replacement of water mains. Journal of water resources planning and management. 2006;132(2): 79-88.

8.  Babu KSJ, Vijayalakshmi DP. Self-Adaptive PSO-GA Hybrid Model for combinatorial Water Distribution Network Design. Journal of Pipeline Systems Engineering and Practice. 2013;4(1):57-67.

9.  Cross H. Analysis of flow in networks of conduits or conductors. USA: University of Illinois; 1936. [Citado 23 octubre 23 enero de 2018] Disponible en: Disponible en: https://www.ideals.illinois.edu/bitstream/handle/2142/4433/engineeringexperv00000i00286.pdf 9.

10.  Rao BV. Finite element analysis of flow net works. Engineering Analysis - Computational Mechanics Publications. 1987;4(1):35-9.

11.  Mageid HA, Hago AW, Abdel Magid IM. Analysis of pipe networks by the finite element method. Water International. 1991;16(2):96-9.

12.  Ezzeldin R, Djebedjian B, Saafan, T. Integer Discrete Particle Swarm Optimization of Water Distribution Networks. Journal of Pipeline Systems Engineering and Practice. 2014;5(1):1-11.

13.  Kadu MS, Gupta R, Bhave PR. Optimal Design of Water Networks Using a Modified Genetic Algorithm with Reduction in Search Space. Journal of Water Resources Planning and Management. 2008;134(2):147-60

14.  Savic DA, Walters GA. Genetic algorithm for least-cost design of water distribution networks. Journal of Water Resources Planning and Management. 1997;123(2): 67-77.

15.  Yeh HD, Lin YC. Pipe network system analysis using simulated annealing. Journal of Water Supply: Research and Technology-Aqua. 2008;57(5):317-27.

16.  Colebrook CF. Turbulent Flow in Pipes, with particular reference to the Transition Region between the Smooth and Rough Pipe Laws. Journal of the Institution of Civil Engineers. 1939;11(4):133-59.

17.  Williams GS, Hazen A. Hydraulic tables. 3rd ed. USA: John Wiley & Sons, Inc.;1933.

18.  Wu ZY, Walski T. Self-Adaptive Penalty Approach Compared with Other Constrainst-Handling Techniques for Pipeline Optimization. Journal of Water Resources Planning and Management. 2005;131(3):181-192.

19.  Gaspar Cunha A, Takahashi RHC, Antunes CH. Manual de Computação Evolutiva e Metaheurística. Brasil: Editora UFMG; 2013.

20.  Scola, L.A.; Takahashi, R.H.C.; Cerqueira, S.A.A.G. Multipurpose water reservoir management: an evolutionary multiobjective optimization approach. Mathematical Problems in Engineering. 2014;7:31-9.

21.  De Azevedo Netto JM, Fernandez Y Fernandez M. Manual de Hidráulica. 8va ed. Brasil: Edgard Blücher Ltda; 1998.

22.  Lee KY, El-Sharkawi MA. Modern Heuristic Optimization Techniques -Theory and Applications to Power Systems. USA: John Wiley & Sons, Inc.; 2008.

Received: October 12, 2018; Accepted: December 03, 2018

^*Corresponding author: [e-mail]