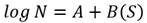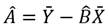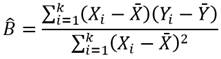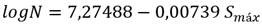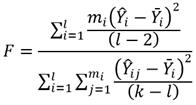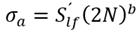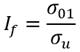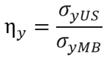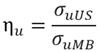Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Las características propias de las uniones soldadas, dadas por las diferencias en las propiedades mecánicas de las diferentes zonas que conforman la unión, es siempre un tema de investigación en la agenda de trabajo de los ingenieros. La Zona de Afectación Térmica (ZAT) de la unión sufre transformaciones metalográficas por los elevados gradientes de temperatura que tienen lugar durante el proceso de soldadura, y por ende, también varían en sus propiedades mecánicas, entre ellas la tenacidad a fractura. Por esta causa, la ZAT es la región más propensa a que ocurra el fallo de la unión cuando es solicitada por cargas variables que favorezcan la nucleación y posterior propagación de grietas. A esto obedece que sea necesario conocer la curva S-N para el diseño y comprobación de las uniones soldadas.
En la investigación [1], se realizó el análisis experimental y numérico del crecimiento de grietas de fatiga en recipientes a presión de paredes gruesas. Se utilizó la Ley de Paris en la evaluación del crecimiento de la grieta.
El tiempo admisible para que los técnicos puedan determinar mediciones relevantes tiene que ser menor que el necesario para que se propague la grieta desde la longitud hasta que se alcance la longitud crítica [2].
La experimentación y la simulación numérica de la trayectoria de propagación de fisuras por fatiga en cinco probetas de acero de alta resistencia se presentaron por [3]. Estos autores alcanzaron resultados prácticamente idénticos entre los resultados experimentales y numéricos, lo que demostró una fuerte correspondencia entre los ensayos reales y la simulación.
Almaguer et al, [4] propusieron ecuaciones para evaluar la eficiencia a la fluencia y a la rotura de uniones soldadas a tope de acero AISI 1015 y electrodo E6013. Estas ecuaciones se utilizan en este trabajo para determinar la eficiencia de la unión estudiada.
Las recientes innovaciones tecnológicas de la soldadura por arco de fusión, están destinadas a mejorar la penetración y la sostenibilidad del proceso de refundición. Al mismo ritmo que las técnicas de soldadura evolucionan, el control de calidad también lo hace porque la posibilidad de fallas siempre está presente [5]. De esto se desprende que los controles en el proceso de soldadura deben estar presentes desde los preparativos para comenzar a fabricar las piezas. Ramalho et al, [6] estudiaron la factibilidad de realizar la reparación por soldadura de uniones soldadas con grietas de fatiga en el pie de la soldadura. Los autores de este trabajo concuerdan con este criterio, siempre que se realice la preparación correcta para realizar las reparaciones, el proceso de soldadura permite recuperar aquellos elementos donde se hayan detectado la presencia de las grietas y de esta manera recuperar su vida útil.
En trabajos recientes [7, 8, 9] se utilizó un coeficente de asimetría igual a 0,1 para realizar investigaciones de fatiga y fractura. Golahmar [10] planteó que para una curva S-N ajustada según el modelo de Basquin se puede obtener una buena estimación cuando esta curva no se desvía de la linealidad. Estas planteamientos son asumidos por los autores de este artículo para desarrollar la evaluación a fatiga de la unión soldada estudiada.
El objetivo de este artículo fue determinar la curva S-N para una unión soldada a tope fabricada mediante el proceso de soldadura por arco con núcleo fundente (FCAW, Flux Core Arc Welding) en la que se empleó el acero AISI 1015 como material base y el material de aportación es el alambre ER71-T. Se obtuvo el límite de resistencia a la fatiga para la unión soldada estudiada. Mediante el ajuste potencial de la relación entre la tensión amplitud y el doble del número de ciclos se determinaron el coeficiente y el exponente de la ecuación de Basquin.
Métodos y Materiales
Para realizar este estudio se empleó un acero AISI 1015 utilizado en la fabricación de máquinas e implementos agrícolas. El material base utilizado para fabricar las uniones soldadas para los ensayos a tracción y a fatiga se usaron chapas de 500 mm x 50 mm x 4 mm. La unión se realizó a tope sin preparación de bordes, con cordones a ambos lados de acuerdo a las dimensiones propuestas en la figura 1. Las formas y dimensiones de estas probetas fueron definidas acorde con la norma NC-ISO 4136: 2014: Ensayos destructivos de soldaduras en materiales metálicos ― Ensayo de tracción transversal. Estos ensayos se realizaron con probetas soldadas con forma de huesos de perro (dog bones). Se ensayaron 20 probetas que antes de ser sometidas al ensayo a fatiga fueron evaluadas mediante inspección visual y después mediante el ensayo de líquidos penetrantes. No se detectaron defectos por los que fuera necesario desechar las probetas. Para definir la cantidad de probetas se siguió el método de la escalera. En principio se ensayaron cuatro probetas en cada nivel de carga. Cuando se terminó con un nivel se pasó al siguiente y así hasta alcanzar el número de ciclos igual a 1 500 000 que se considera como vida infinita para el caso de las uniones según la norma ASTM 739-91. Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ɛ-N) Fatigue Data. En esta investigación se logró en el quinto nivel de carga.
Para corroborar que el material empleado en los experimentos fuera el acero AISI 1015, el suministrador del acero, la empresa AMF Acero y Materiales Ferrosos localizada en Monterrey, Estado Nuevo León, en México, proporcionó un certificado de calidad. En la tabla 1 se encuentra la composición química típica del acero y la que proporcionó el fabricante. La comparación entre los principales elementos posibilita corroborar que se trata del acero AISI 1015. La composición química y las propiedades mecánicas del material base según la bibliografía está en la tabla 1.
Tabla 1 Composición química y propiedades mecánicas del acero AISI 1015. Fuente: http://www.matweb.com
| Composición | Típica | Fabricante | Propiedad | Valor |
|---|---|---|---|---|
| Carbono (%) | 0,13- 0,18 | 0,160 | Tensión última σu (MPa) | 420 |
| Manganeso (%) | 0,30 - 0,60 | 0,550 | Límite elástico σy (MPa) | 315 |
| Silicio (%) | 0,17 - 0,37 | 0,180 | Coeficiente de Poisson µ | 0,29 |
| Azufre (%) | ≤0,05 | 0,027 | Alargamiento relativo δ (%) | 39 |
| Fósforo (%) | ≤0,04 | 0,019 | Estricción de área ψ (%) | 61 |
La unión soldada se fabricó mediante un proceso de soldadura por arco con núcleo fundente FCAW. El material de aporte fue el alambre ER71-T. La presentación del alambre es en bobinas. El diámetro de la sección transversal es de 1,58 mm. Este alambre está formulado para depositar soldaduras de alta calidad y se utiliza para la soldadura de acero al carbono, de baja aleación, estructural y para recipientes a presión. Los parámetros del proceso de soldadura fueron: intensidad de la corriente 145 A, tensión 14,3 V, velocidad de soldadura 1 mm/s, el gas de protección fue dióxido de carbono y se utilizó una máquina Miller modelo CP-302.
Acorde con los datos presentados por la empresa Soldexa (http://www.soldexa.com.pe) el límite elástico σy y la tensión última σu del depósito son iguales a 529 MPa y 578 MPa, respectivamente. Como se aprecia, la tensión última del material de aporte es mayor que la del material base, referida en la tabla 1, por lo tanto, la selección de este alambre es posible.
Las uniones soldadas son concentradores de tensiones debido al cambio de sección entre el metal base y el sobrecordón. A ello se suma la disminución de la tenacidad en la ZAT; lo que propicia el fallo de la unión ante las cargas variables.
La unión soldada objeto de estudio fue ensayada a fatiga, para ello fue necesario determinar los valores de los parámetros del ciclo de carga. El régimen de carga empleado fue a tracción asimétrica con un coeficiente de asimetría R igual a 0,1 que se utilizó por otros autores [7, 8, 9]
Se realizaron ensayos a tracción acorde con la norma ASTM E 8-04, en una máquina universal MTS-810 de fabricación estadounidense. Esta máquina se encuentra en el Laboratorio de Pruebas Mecánicas y Ensayos No Destructivos del Centro de Investigación e Innovación en Ingeniería Aeronáutica (CIIIA), de la Universidad Autónoma de Nuevo León, México. La capacidad de carga de la máquina es de 250 kN. El agarre en forma de cuñas por accionamiento hidráulico asegura la sujeción de las probetas. El software de control de la máquina es el MTS FlexTest 40. La probeta se inmovilizó en el cabezal fijo de la máquina, mientras que en el cabezal móvil se aplicó un desplazamiento a una velocidad de 0,1 mm/s. Se estudiaron tres probetas soldadas. Este ensayo se hizo con el propósito de conocer el límite elástico de la unión y a partir de ella determinar la tensión máxima ?#61555; max a aplicar en el primer nivel de carga cíclica. De esta manera el límite elástico ?#61555;y promedio obtenido es igual a 322,71 MPa.
La tensión máxima del ciclo ?#61555; max en un primer nivel de carga se tomó como el 90 % del límite elástico de la unión estudiada, ecuación (1). Para decidir esto se consideró que la fatiga del elemento ocurre a valores de tensión inferiores al límite de fluencia.
(1)
El valor de la tensión máxima calculada mediante la expresión anterior es igual a ?#61555; max = 290,4 MPa, a la que corresponde una carga máxima P max = 17 427 N.
En esta investigación, los siguientes niveles de carga se determinaron a medida que se avanzó en la realización de los experimentos. Para determinar los parámetros de cada nivel de carga se hizo una disminución en el valor de la tensión máxima ?#61555; max igual al 10 % del límite elástico ?#61555; y . Esto se debió a la gran dispersión que existe en los resultados de los ensayos a fatiga. La lógica que se siguió para determinar los siguientes niveles de carga fue la siguiente: se disminuyó el valor de carga hasta que las probetas ensayadas igualaron o superaron el valor de 1 500 000 ciclos, para los que se corresponde el límite de resistencia a la fatiga en el caso de las uniones según la norma ASTM E 739 - 91. Para los ensayos se fijó la razón de asimetría del ciclo R = 0,1. La frecuencia de aplicación de la carga fue de 5 Hz. Como criterio de fallo se utilizó el de fractura total. El ensayo se interrumpía cuando eran aplicados 1 500 000 ciclos de carga. La temperatura del laboratorio era de 23 ºC ( 2 ºC.
Los ensayos se realizaron a cinco niveles de carga. Esto obedeció a la forma en que se desarrollan los experimentos a fatiga. Para obtener el límite de resistencia a la fatiga se ensayan probetas a valores de carga que se disminuyen, de manera empírica, hasta que varias probetas resistan el número de ciclos necesarios para considerar que se alcanzó dicho límite. Esta manera de realizar los ensayos a fatiga se conoce como método de la escalera o sube y baja.
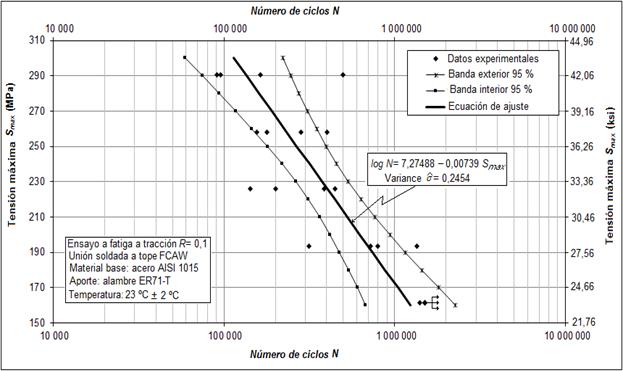
Otra norma utilizada para configurar los ensayos a fatiga fue la norma ASTM E 468 - 90. A partir de esta se determinó la información necesaria a obtener en el ensayo para la posterior presentación de los resultados y la construcción de la curva S - N. La curva se obtuvo a partir de los datos experimentales procesados según ASTM E 739 - 91 y se ajustó con un modelo lineal. El punto de corte se encuentra para una tensión máxima igual al límite de resistencia a la fatiga σ01 (161,4 MPa) y 1 091 190 ciclos.
Los ensayos a fatiga se realizaron en la misma máquina universal MTS-810 que se utilizó para los ensayos a tracción.
En la tabla 2 se muestran la amplitud del ciclo σa y la tensión máxima Smax. Los dos valores de tensión se expresan tanto en el Sistema Internacional de Unidades como en el Sistema Inglés para facilitar la búsqueda de algún valor. También se encuentran el número de ciclos que resistió cada probeta y se realizan observaciones sobre la naturaleza del fallo. Según la norma ASTM E 468 - 90 solo es necesario presentar dos parámetros del ciclo en la tabla de los resultados de los ensayos.
Tabla 2 Resultados del ensayo a fatiga. Fuente: autores
| Probeta |
|
|
Ciclos | Observaciones |
|---|---|---|---|---|
| 1 | 130,68/18,95 | 290,40/42,12 | 500 701 | Falló en la ZAT |
| 2 | 130,68/18,95 | 290,40/42,12 | 95 713 | Falló en MA |
| 3 | 130,68/18,95 | 290,40/42,12 | 90 890 | Falló en la ZAT |
| 4 | 130,68/18,95 | 290,40/42,12 | 163 078 | Falló en la ZAT |
| 5 | 116,20/16,85 | 258,20/37,45 | 155 641 | Falló en la ZAT |
| 6 | 116,20/16,85 | 258,20/37,45 | 403 269 | Falló en MA |
| 7 | 116,20/16,85 | 258,20/37,45 | 28 084 | Falló en la ZAT |
| 8 | 116,20/16,85 | 258,20/37,45 | 178 750 | Falló en la ZAT |
| 9 | 101,70/14,75 | 225,90/32,76 | 384 777 | Falló en MA |
| 10 | 101,70/14,75 | 225,90/32,76 | 448 974 | Falló en la ZAT |
| 11 | 101,70/14,75 | 225,90/32,76 | 142 170 | Falló en la ZAT |
| 12 | 101,70/14,75 | 225,90/32,76 | 201 759 | Falló en MA |
| 13 | 87,10/12,63 | 193,60/28,08 | 1 350 568 | Falló en la ZAT |
| 14 | 87,10/12,63 | 193,60/28,08 | 725 597 | Falló en la ZAT |
| 15 | 87,10/12,63 | 193,60/28,08 | 316 073 | Falló en la ZAT |
| 16 | 87,10/12,63 | 193,60/28,08 | 797 389 | Falló en la ZAT |
| 17 | 72,60/10,53 | 161,4/23,41 | 1 400 000 | Falló en la ZAT |
| 18 | 72,60/10,53 | 161,4/23,41 | 1 500 000 | No falla |
| 19 | 72,60/10,53 | 161,4/23,41 | 1 500 000 | No falla |
| 20 | 72,60/10,53 | 161,4/23,41 | 1 500 000 | No falla |
En el caso de las probetas 18, 19 y 20 que fueron ensayadas en el quinto nivel de carga y no fallaron se examinaron mediante líquidos penetrantes después de ser retiradas de la máquina de ensayo a fatiga. Estas no mostraron haber desarrollado grietas superficiales que pudieran ser identificadas mediante esa prueba.
Para el tratamiento de los resultados de los ensayos a fatiga se aplicó en esta investigación la norma ASTM E 739 - 91 que rige el tratamiento estadístico de los mismos.
La distribución de vida de fatiga (en cualquier ensayo) es desconocida y de hecho puede ser bastante compleja en ciertas situaciones. Para los propósitos de simplificar el análisis, se supone en la práctica que se describe en la norma ASTM E 739 - 91 que el logaritmo del número de ciclos a fatiga sigue una distribución normal, y que la varianza del logaritmo de la vida a fatiga es constante en todo el rango de la variable independiente (es decir, se asume que la dispersión en el logaritmo de N es la misma tanto a bajos como a altos niveles de tensión o deformación).
De manera general, es posible relacionar la vida a fatiga con la tensión del ciclo mediante la ecuación (2):
(2)
Donde:
A y B: son los coeficientes de ajuste de la ecuación (2).
El logaritmo de N se usa como la variable dependiente y se denota por Y; mientras que la variable independiente se denota por X y puede ser la tensión S, la deformación ?#61541;, el logaritmo de la tensión logS o el logaritmo de la deformación log?#61541;. En este estudio se utiliza la tensión máxima del ciclo, que la denotamos como S max .
De acuerdo a lo planteado aquí la linealización de la dependencia entre N y S max toma la forma de la ecuación (3):
(3)
El tamaño de la muestra k, de acuerdo a la misma norma mencionada antes puede estar entre 12 y 24 para datos confiables. En esta investigación fue de 20 probetas ensayadas.
El porciento de replicación es igual al 75 %. Se le debe prestar atención a que el porciento de replicación indica que porción de la cantidad de probetas ensayadas puede ser usada para obtener una estimación de la variabilidad de los ensayos replicados. La norma ASTM E 739 - 91 plantea que debe estar entre 75 % y 88 %. El valor calculado en esta investigación corresponde a 15 probetas. Como sea se realizaron las estimaciones en base a las 20 probetas ensayadas.
Los estimadores para los coeficientes de la ecuación (2) se determinaron mediante las ecuaciones (4) y (5).
(4)
(5)
Los símbolos casquete (˄) y barra superior (¯) significan estimador y valor medio respectivamente.
Los valores de los estimadores así calculados son  = 7,27488 y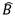 
= -0,00739.
Sustituyendo estos valores en la ecuación (2) se obtiene la ecuación (6) que relaciona el número de ciclos N y la tensión máxima del ciclo Smax:
(6)
La varianza del logaritmo del número de ciclos es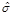 
= 0,2454.
Los intervalos de confianza para los valores de A y B pueden ser establecidos usando la distribución t que aparece en ASTM E 739 - 91.
Los intervalos de confianza así determinados son los siguientes:
Ahora es necesario probar la certeza del uso del modelo lineal asumido en la ecuación (3). Si el ensayo es realizado de manera tal que sean observados más de un valor de Y para algunos valores de X i (X i son los niveles de carga e i ≥ 3) entonces es posible realizar una prueba estadística basada en la distribución F que aparece en la norma ASTM E 739 - 91. El logaritmo de N en la j-ésima probeta ensayada en el i-ésimo nivel de X i es denotado para este análisis como Y ij .
En este estudio los ensayos a fatiga se realizaron a l= 5 diferentes niveles de carga y fueron observados diferentes valores m i de Y ij en cada valor de X i . Para cada nivel de carga X i aparecen los diferentes valores observados de Y ij en la tabla 2. La hipótesis de linealidad expresada en la ecuación (3) es rechazada cuando el valor de F calculado usando la ecuación (7) es mayor que F p determinado en ASTM E 739 - 91. Para el nivel de significancia deseado del 95 % F p es igual a 3,6823.
(7)
El parámetro F calculado tiene un valor de 1,173 que es menor que F p por lo tanto se acepta la hipótesis de linealidad del modelo que se emplea para el estudio de los resultados del ensayo a fatiga de la unión soldada.
Los puntos experimentales se ajustaron a una ecuación potencial para determinar las constantes de la ecuación de Basquin (8). Mediante la ecuación (9) se determinó el índice de fatiga I f , que es el cociente entre el límite de fatiga ?#61555; 01 y la resistencia a la tracción ?#61555; u de la unión soldada [11]. Este índice I f es igual a 0,37.
(8)
(9)
Se calcularon los parámetros de eficiencia. Esta se define como la razón entre la propiedad de la unión soldada y la del material base. De esta manera las eficiencias a fluencia ?#61544;y y y a rotura rotura ?#61544;u se determinaron según la ecuación (10) y la ecuación (11). Los subíndices US y MB se refieren a la unión soldada y al material base respectivamente.
(10)
(11)
Se realizó un análisis fractográfico a todas las probetas que fallaron a fatiga mediante microscopía electrónica de barrido, SEM (Scanning Electron Microscopy, sigla en inglés). Con el objetivo de realizar este análisis se utilizó un microscopio electrónico de barrido marca JEOL Modelo LV 650. El equipo se encuentra en el Laboratorio de Análisis de Falla del Centro de Investigación e Innovación en Ingeniería Aeronáutica (CIIIA) de la Universidad Autónoma de Nuevo León.
Resultados y Discusión
Se realizó la caracterización mecánica y se obtuvo la curva S-N para la unión soldada a tope de acero AISI 1015 y alambre ER71-T fabricada mediante el proceso FCAW. De esta manera se conocen propiedades mecánicas de la unión como el límite elástico, la tensión última y el límite de resistencia a la fatiga.
Propiedades mecánicas de la unión soldada
En la figura 2a se encuentran las probetas soldadas rotas después de ser traccionadas. Se ve como la rotura de las tres ocurrió en el material base y no en la zona fundida. Esto muestra que se cumple el objetivo de que la unión soldada no falle en el material de aporte, y sí en el material base.
Fuente: autoresFig. 2 a) Probetas rotas después de ser traccionadas. b) Curvas tensión-deformación de las probetas ensayadas.
En la figura 2b se muestran los gráficos de tensión-deformación obtenidos de los ensayos a tracción realizados en la máquina MTS810 a las probetas de las uniones soldadas. Se denotan como T01, T02 y T03.
La tabla 3 muestra las diferentes propiedades determinadas con el ensayo a tracción (Límite elástico ?#61555; y y la tensión última ?#61555; u ). La columna Plasticidad se refiere a los parámetros Coeficiente de resistencia K y Exponente de endurecimiento por deformación n para ajustar la relación entre la tensión y la deformación en la zona plástica a través de una ecuación del tipo Hollomon.
Ensayos a fatiga
En la tabla 4 se encuentran los valores de los parámetros de cada ciclo a los que se realizaron los ensayos.
Tabla 4 Parámetros de los ciclos de carga para los diferentes niveles a los que se realizaron los ensayos a fatiga. Fuente: autores
| Nivel | |||||
|---|---|---|---|---|---|
| Parámetro | 1 | 2 | 3 | 4 | 5 |
| Carga máxima |
17 427,00 | 15 490,00 | 13 554,00 | 1 1618,00 | 9 681,00 |
| Carga mínima |
1 742,70 | 1 549,00 | 1 355,40 | 1 161,80 | 968,10 |
| Carga media |
9584,85 | 8519,50 | 7454,70 | 6389,90 | 5324,55 |
| Carga amplitud |
7842,15 | 6970,50 | 6099,30 | 5228,10 | 4356,45 |
| Rango de la carga |
15684,30 | 13941,00 | 12198,60 | 10456,20 | 8712,90 |
| Tensión máxima |
290,40 | 258,20 | 225,90 | 193,60 | 161,40 |
| Tensión mínima |
29,04 | 25,80 | 22,59 | 19,30 | 16,10 |
| Tensión media |
159,72 | 142,00 | 124,20 | 106,50 | 88,70 |
| Tensión amplitud |
130,68 | 116,20 | 101,70 | 87,10 | 72,60 |
| Rango de tensión |
261,36 | 232,38 | 203,31 | 174,24 | 145,26 |
| Coeficiente de asimetría |
0,1 | ||||
En el quinto nivel una probeta resistió 1 400 000 ciclos de carga mientras que tres probetas resistieron 1 500 000 ciclos sin fallar por lo que se procedió a detener el ensayo y considerar que el valor de tensión máxima ( max igual a 161,4 MPa es el límite de resistencia a la fatiga ?#61555; 01 para la unión estudiada.
La presentación de los resultados del ensayo a fatiga se realiza según la norma ASTM E 468 - 90 Standard Practice for Presentation of Constant Amplitude Fatigue Test Results for Metallic Materials. En esta se dice que exponen datos como las características del material base, procesos tecnológicos realizados, probetas utilizadas, máquina de ensayos utilizada, condiciones de los experimentos para que se le pueda dar a la información proporcionada la mayor utilidad posible y que sea posible replicar los mismos. Esos datos se mencionaron antes.
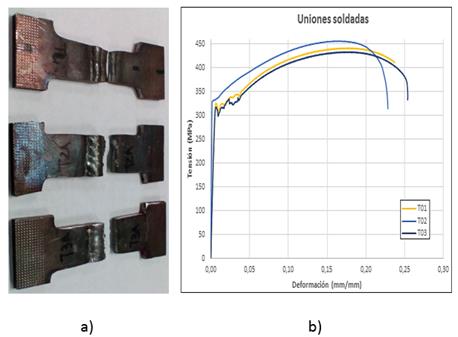
La máquina de ensayos utilizada permite grabar los gráficos de tensión-deformación en determinados ciclos de carga. En este estudio se obtuvieron en los dos primeros y en los dos últimos ciclos. En la figura 3, se exponen, a modo de ejemplo, estos gráficos para la probeta 14. Se observa como en los primeros ciclos de carga hay mayor área debajo de la curva que en los últimos. A juicio de los autores esto se debe a las dimensiones de la grieta. Cuando la grieta es pequeña, la probeta tiene mayor resiliencia, no así cuando se está cerca de la rotura final, donde la grieta ha aumentado su tamaño hasta valores cercanos a la longitud crítica. Este comportamiento se observó en las 17 probetas que fallaron.
Fuente: autoresFig. 3 Gráficos de tensión - deformación para la probeta F14. a) Ciclo 1. b) Ciclo 2. c) Ciclo 725 596. d) Ciclo 725 597.
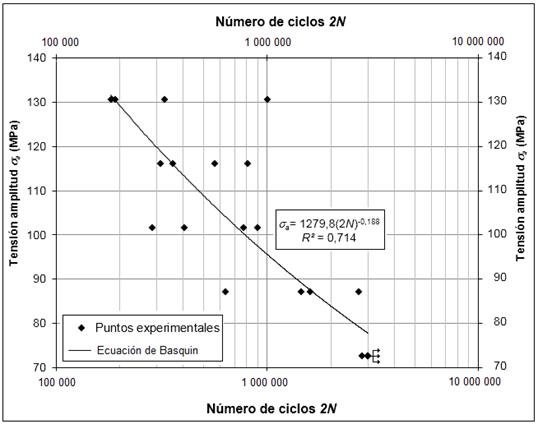
Como se aprecia en la figura 4, el coeficiente de resistencia a la fatiga S´ lf y el exponente b de la ecuación de Basquin son iguales a 1 279,8 MPa y -0,188, respectivamente. El ajuste R² es igual a 0,714. Debido a la gran dispersión que se aprecia en los resultados experimentales del ensayo a fatiga es posible considerar este valor como bueno. Las tres probetas a las que se les interrumpió el ensayo sin que ocurriera el fallo están marcadas con flechas.
Curva S-N de la unión ensayada
En la Figura 5 está la curva S-N de la unión soldada ensayada en este estudio. Como se observa 15 puntos experimentales se encuentran dentro de las bandas de confianza del 95 %. Este resultado indica el buen ajuste obtenido con el modelo lineal asumido para obtener la curva. El ensayo se interrumpió en el quinto nivel de carga a una tensión máxima igual a 161,4 MPa. En la curva de ajuste, a este valor de tensión se corresponde un número de ciclos igual a 1 091 190.
Análisis fractográfico
En la figura 6 se muestra, a modo de ejemplo, la observación realizada a la probeta F14. Esta probeta fue ensayada a una tensión máxima de 193,6 MPa y una amplitud de 87,1 MPa. El número de ciclos que soportó fue igual a 725 597 y el fallo se produjo en la ZAT. Se señala el inicio de la grieta de fatiga y la posición del frente de la grieta en el momento en que ocurrió la fractura. Se aprecia la diferencia de textura entre la zona donde creció la grieta y en la que tuvo lugar la rotura frágil debido a la sobrecarga estática. También se observa la estricción característica del fallo por tracción.
Es de destacar que la forma de los fallos en todas las probetas es similar. La grieta siempre se inició en un defecto, que puede ser propio del material, de los procesos de mecanizado para la fabricación de las probetas y los más importantes en este aspecto, los de la soldadura, pues fueron los que más influyeron en las fallas. Se observó que el crecimiento de la grieta fue con un frente semielíptico hasta que ocurría la rotura final.
En investigaciones anteriores [12] se asumió un modelo lineal para el procesamiento de los datos experimentales y se obtuvo un buen ajuste de la curva S-N mediante el uso de la norma ASTM 739, resultado que concuerda con los obtenidos en este trabajo. Otros autores [13] también observaron como las grietas se iniciaron en un defecto y luego crecieron hasta consumir la vida a fatiga, propagándose en un frente semielíptico [14]. En otros resultados experimentales [15] también se observó que las grietas nuclearon un defecto al pie del cordón de soldadura que es el lugar con mayor probabilidad de iniciación y crecimiento de las grietas de fatiga en las uniones soldadas. En todas las probetas que fallaron se observó la zona donde se desarrolló la grieta y la zona de rotura frágil, donde ocurre una estricción debida a la sobrecarga estática, lo que concuerda con los resultados presentados por [16]. Estos mismos resultados muestran que la resistencia a la fatiga de la unión se ve afectada por la concentración de tensiones en los cambios de sección propios de la geometría del cordón como se demostró también en [17].
Conclusiones
El ensayo a fatiga realizado con probetas soldadas a tope por el proceso FCAW de acero AISI 1015 y alambre ER71-T permitió determinar la curva S-N de la unión. De acuerdo con el ajuste lineal realizado a la ecuación (2) se puede considerar que el límite de resistencia a la fatiga de la unión se corresponde con la tensión máxima igual a 161,4 MPa; a un punto de corte de 1 091 190 ciclos. La dispersión observada en los resultados experimentales obedece a las características propias del fenómeno de la fatiga.
