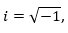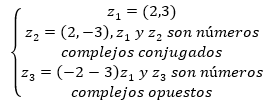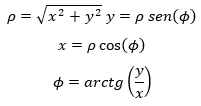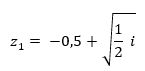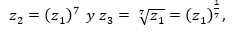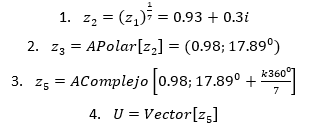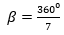Introducción
El concepto de número complejo apareció como resultado de la necesidad de los matemáticos de sistematizar los cálculos y esta necesidad se evidenció desde épocas relativamente tempranas, ya que hasta las más sencillas operaciones algebraicas con números reales se salen del marco del campo de estos números.
Ejemplo, es conocido que no toda ecuación algebraica puede ser resuelta con números reales; por consiguiente, es necesario renunciar a la aplicación automática de los métodos de solución establecidos y en cada caso investigar minuciosamente las posibilidades de aplicación de dichos métodos o ampliar el campo de los números reales, de manera que las operaciones algebraicas fundamentales sean siempre aplicables. Tal ampliación es, precisamente, el concepto de número complejo.
Generalmente, en la Enseñanza Media Superior o Bachillerato de muchos países se imparten los números complejos, como es el caso de Cuba, pero donde este tema si es indispensable es en la introducción del estudio de las Funciones Analítica como es el caso del Instituto Superior de Ciencias de la Educación en la República de Angola.
En ese contexto, se han detectado dificultades en el proceso de enseñanza-aprendizaje concernientes a:
La relación entre el cálculo algebraico y la representación gráfica de los resultados, jerarquizándose el primero y descuidando el segundo, porque generalmente tal representación en forma manual le resulta engorrosa a la mayoría de los alumnos.
Expresar los números complejos en forma trigonométrica y su empleo resulta un problema para los alumnos, pese a que ellos se emplean para simplificar el cálculo ante situaciones como la potenciación de números complejos, ya que calcular
resulta complicado y para el cálculo de raíces donde se presenta una situación similar.
Una alternativa de solución de estas u otras situaciones análogas es el empleo de asistentes matemáticos como medio auxiliar heurístico, particularmente el software Geogebra con el que los autores han desarrollado otras experiencias. (Toto, 2017).
Desarrollo
La propiedad fundamental de los números complejos es que las operaciones matemáticas con ellos realizadas no se salen de los límites de su definición.
El concepto de número complejo puede serle familiar al lector de los cursos de álgebra elemental, no obstante, recordaremos que en dichos cursos generalmente se llega a este concepto al analizar la ecuación. (Crespo, 2007)
x2 + 1 = 0
Lo primero que se observa es que no existen números reales que satisfagan dicha ecuación. Por eso se introduce un nuevo número “imaginario”
con ayuda del cual la citada ecuación resulta soluble y cuyas raíces son +i 𝑦−𝑖.
La historia recoge que la primera referencia a los números “imaginarios” como las raíces cuadradas de números reales negativos se remonta al siglo XVI (Cardano, 1545); (Churchill, 1996). Hasta la mitad del siglo XVIII los números complejos aparecen en algunos trabajos aislados de diferentes matemáticos (Newton, Bernoulli, Clairaut). En la segunda mitad del siglo XVIII se introduce el símbolo i y comienza un desarrollo sistemático de la teoría de los números complejos en los trabajos de eminentes matemáticos y físicos como Leonard Euler, August Cauchy, Karl Weierstrass, Bernhard Riemann, Casper Bessel y otros.
Inmediatamente después de resolver
x2 + 1 = 0
x2 + 2x + 2 = 0
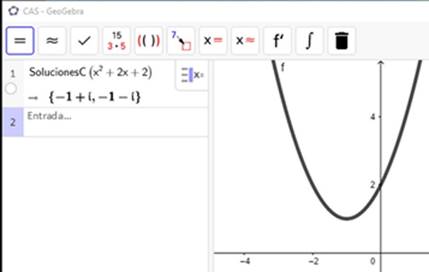
Utilizando el asistente Geogebra la solución de esta ecuación se muestra en la siguiente imagen, donde se utiliza el cálculo simbólico (CAS) que posee esta aplicación. Ver (figura 1)
Las soluciones son:
x1 = -1 + i; x2 = - 1 - i
Observe que la curva que representa la función
f(x)=x2+2x+2
no corta el eje de abscisas, por eso la ecuación no tiene soluciones en el conjunto de los números reales.
Una vez introducidos estos números, de la forma
a + bi
con el que se define un número complejo, todas las ecuaciones de segundo grado y en general cualquier ecuación de la forma
xn+p_1 xn-1+p2 xn-2+⋯+ pn=0
con coeficientes arbitrarios tienen soluciones en el conjunto de los números complejos.
Geogebra:
GeoGebra es un software de matemática que reúne geometría, álgebra y cálculo. Lo ha desarrollado Markus Hohenwarter (2009) en la Universidad de Salzburgo para la enseñanza de matemática escolar.
Por un lado, GeoGebra es un sistema de geometría dinámica. Permite realizar construcciones tanto con puntos, vectores, segmentos, rectas, secciones cónicas como con funciones que a posteriori pueden modificarse dinámicamente.
Por otra parte, se pueden ingresar ecuaciones y coordenadas directamente. Así, GeoGebra tiene la potencia de manejarse con variables vinculadas a números, vectores y puntos; permite hallar derivadas e integrales de funciones y ofrece un repertorio de comandos propios del análisis matemático, para identificar puntos singulares de una función, como Raíces o Extremos.
Estas dos perspectivas caracterizan a GeoGebra: una expresión en la ventana algebraica se corresponde con un objeto en la ventana geométrica y viceversa.
Definición de número complejo con Geogebra:
Se llama número complejo o simplemente complejo a un número de la forma
z = x + iy
Donde:
x ∈ R ; y ∈ R.
El número x se denomina parte real del número complejo
x = Re(z)
y el número y se denomina parte imaginaria del número complejo
y = Im (z).
Esta forma de definición se conoce como forma binómica, forma algebraica, o forma de Descartes del número complejo. Otra forma de dar esta definición, es como un par ordenado
z = (x , y)
Ambas formas se pueden representar geométricamente como se muestra a continuación y parte de la posibilidad del Geogebra de asignar un punto del plano cartesiano a cualquier número
Zk=x+iy
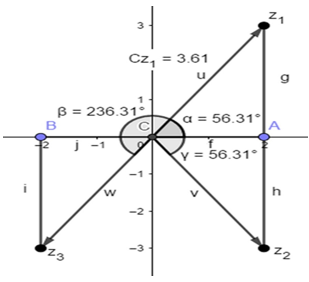
como se muestra en la siguiente (imagen 2) generada en Geogebra:
Obsérvese que respecto a
se z1 = (2,3)
tiene dos números
z2=(2,-3) y
z3=(-2-3)
con características particulares:
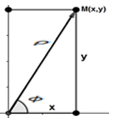
La tercera forma de presentar el número complejo es la forma trigonométrica mediante las siguientes expresiones:
Con : Ver (figura 3)
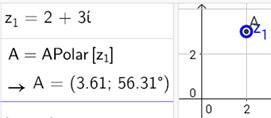
Pero estas fórmulas, que tienen un gran valor teórico-conceptual, se pueden obtener de dos formas en Geogebra, a partir del menú de medidas, o utilizando el comando
A Polar[ <Complejo> ], el cual devuelve el módulo y el argumento del número complejo como se muestra en la siguiente (imagen 4):
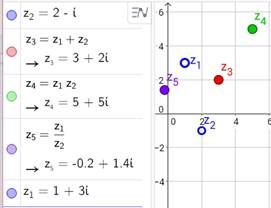
Operaciones aritméticas de números complejos con Geogebra.
Las operaciones aritméticas elementales con números complejos se desarrollan como simples expresiones de cálculo como se dan en los ejemplos. Ver (figura 5):
Potencias y raíces de números complejos con Geogebra.
Se ha pospuesto el cálculo de la potencia y la raíz por las particularidades de estas operaciones. En estos casos la práctica indica expresar primero en forma trigonométrica el número complejo seleccionado para operar con él.
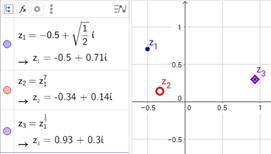
Supongamos que el número seleccionado sea
y deseamos calcular
realmente la tarea es difícil, pero con Geogebra se puede resolver del siguiente modo. Ver (figura 6):
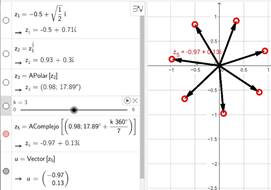
Si se quiere expresar estos resultados a forma trigonométrica, basta con utilizar el comando APolar ya mencionado, pero con el cálculo de la raíz mediante 𝑧 1 1 7 sólo se obtiene la raíz principal, el problema ahora es cómo obtener las demás raíces.
La respuesta se da en la siguiente (gráfica 7)
El algoritmo seguido es el siguiente:
El parámetro k (en 3) genera la necesidad de crear un deslizador, con la condición de variar entre 0 y 7 con incremento 1.
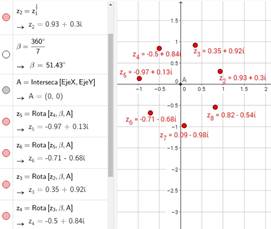
El algoritmo descrito transcribe a Geogebra el cálculo manual de la raíz n-sima de un numero complejo; pero existe otra posibilidad, la de calcular la raíz principal y después rotar ese vector un ángulo
Ejemplo:
de esta forma a partir de una raíz inicial
(en este caso) se obtienen todas las raíces como se muestra en la siguiente( imagen 8):
Conclusiones
En la alternativa propuesta se destacan se ha logrado un equilibrio entre el cálculo algebraico y la representación gráfica de los resultados.
Los problemas derivados del cálculo de potencias y raíces mediante la representación trigonométrica de los números complejos han sido mitigados, manteniendo los fundamentos teóricos-conceptuales del tema.