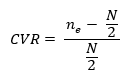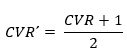Introducción
En su plan de modernización de la Educación de cara al Siglo XXI, el gobierno panameño, ha realizado grandes esfuerzos económicos tanto en la capacitación del personal docente como en la renovación de los programas de estudio de las distintas disciplinas del currículo educativo nacional tales como Ciencias Naturales, Inglés, y Matemáticas, y entre sus políticas educativas, utilizadas por el Ministerio de Educación, ha adoptado la Teoría Cognitivista como teoría de aprendizaje para la ejecución de los nuevos programas curriculares. Sin embargo, según Molina (2017), cinco por ciento de los que cursaron la primaria el año 2017 repitieron el año escolar. Por otra parte, datos ofrecidos en el informe del Programa de Promoción de la Reforma Educativa en América Latina y el Caribe (2007), afirman que más del cincuenta por ciento de los estudiantes han presentado un bajo nivel de rendimiento.
Según Lebrija & Sáenz (2014), en Panamá, los índices de fracasos de los estudiantes de los niveles de la premedia son muy altos, y las bases académicas de los estudiantes al tratar de ingresar a la universidad son muy deficientes. También, Alsina (2007), sugiere la posibilidad de realizar adecuaciones al modelo de enseñanza preescolar y primaria relacionados a la resolución de problemas.
Los grandes avances en áreas de la Matemática tales como Análisis Numérico, Simulación Matemática y Computación, el crecimiento y continuo desarrollo de la Tecnología, y los redescubrimientos de la Psicología y la Sociología; y los nuevos objetivos y metas que la sociedad actual está demandando a los sistemas educativos (Castillo Arredondo, 2007), nos sugieren la necesidad de una revisión de contenidos, métodos y técnicas para enseñar y aprender matemáticas e idiomas en las escuelas primarias de Panamá. Además, la enseñanza y aprendizaje de la matemática requiere especial esfuerzo, y los gobiernos y la sociedad actual deben valorar a esta disciplina como una de las columnas principales para promover el desarrollo científico y tecnológico de la sociedad panameña (Morales, García & Durán, 2019).
El maestro de hoy debería saber que “el proceso del aprendizaje del alumno debe basarse, en su propia actividad creadora, en sus descubrimientos personales, en sus motivaciones intrínsecas, debiendo ser las funciones del profesor la de orientar, guiar; animar, pero no la fuente fundamental de la información”. (Cattaneo, Lagreca & González, 2010, p. 24)
El dominio de las competencias aritméticas no es fácil, y el maestro debe lograr que sus alumnos expresen sus ideas matemáticas. Por ello, es importante que los alumnos adquieran “un vocabulario concreto, así como los medios de expresión y fases que son específicamente matemáticas”. (Lee, 2010, p. 12)
Igualmente, se observa que el contenido de matemáticas en el currículo no ha sufrido modificaciones valiosas, a pesar, del avance significativo de la Matemática, en áreas como Análisis Numérico, Simulación Matemática y de la Computación, de su gran perspectiva de desarrollo sin precedentes para los próximos años, y del papel preponderante en el desarrollo económico y social de los pueblos. Un aspecto psicológico y social que surge para esta era, es el hecho de que estamos frente a una generación diferente, ávida de tener experiencias que muestren que son capaces de analizar, interpretar, comprender y aplicar conocimientos aritméticos y otros en la solución de problemas concretos. Por las razones expuestas, nos parece relevante, determinar si los estudiantes de primer grado de la escuela primaria cuentan con las competencias para resolver problemas aritméticos aplicados a la vida real, a través de un instrumento validado y confiable.
Materiales y métodos
Se trata de un estudio transversal descriptivo mediante un diseño no experimental para medir si el estudiante de primer grado la escuela primaria pública de la provincia de Coclé cuenta con las competencias aritméticas para resolver problemas aplicados a la vida real.
La investigación está dirigida a los estudiantes del primer grado de la escuela primaria, de la educación pública, de la provincia de Coclé.
El presente estudio se llevará bajo una metodología tanto cuantitativa como cualitativa, y desarrollando los siguientes puntos:
Se desarrolló una investigación descriptiva con el propósito de analizar situaciones, eventos y hechos que se constituyen en los antecedentes del trabajo.
Se elaboraron instrumentos de cuantificación de datos, evaluados por el Panel de Expertos.
Se llevarán a cabo análisis estadísticos a los resultados obtenidos a través de la prueba piloto, y se determinará la fiabilidad del mismo a través del Alfa de Cronbach.
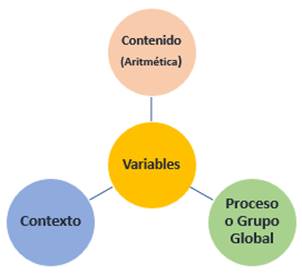
Variables
Las variables de estudio de la presente investigación se muestran en la Figura 1.
Primera Etapa
Para la recolección de la información, se elaboró un instrumento de selección múltiple, basado en el estudio de las variables de contenido (aritmética), contexto y procesos.
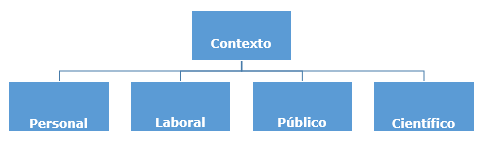
Contextos
Los ítems del instrumento fueron elaborados atendiendo a uno de los contextos que se muestra en la Figura 2.
Competencias matemáticas
El instrumento es un diseño original, compuesto por un total de 80 ítems, y de acuerdo a las características del ítem, cada ítem fue asociado a una competencia matemática. Las competencias matemáticas (Organización para la Cooperación y el Desarrollo Económico, 2017) a estudiar en esta investigación son: Pensar y razonar, argumentación, comunicación, construcción de modelos, formulación y resolución de problemas, representación, empleo de operaciones y de un lenguaje simbólico, formal y técnico y empleo de soporte y herramientas.
Estas competencias pueden ser desarrolladas por los estudiantes a través de distintos procesos o grupos globales de competencia. A continuación, presentamos los procesos cognitivos que desarrollan los estudiantes a la hora de enfrentarse con el proceso de resolución de problemas.
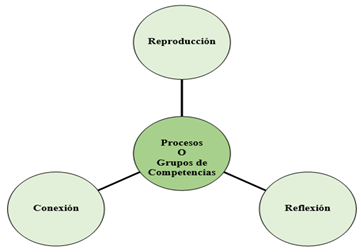
Procesos o Grupos Globales
Cada ítem fue asociado a una competencia matemática, de acuerdo a los indicadores dados. Según la magnitud de la complejidad del proceso cognitivo, las competencias matemáticas son distribuidas de acuerdo a los siguientes grupos globales: reproducción, conexión y reflexión (Figura 3).
A continuación, realizamos una breve descripción de los escribimos los indicadores utilizados para clasificar los ítems por grupo o proceso.
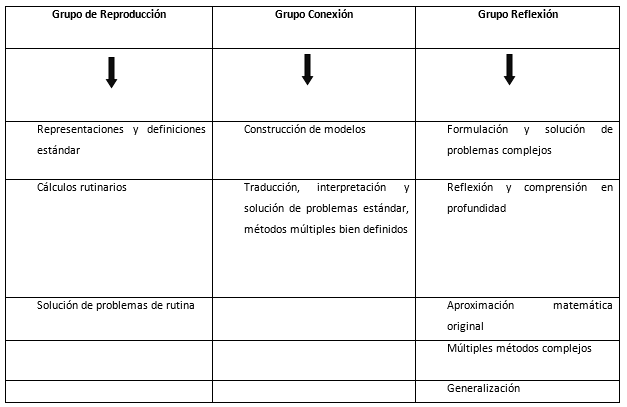
Proceso o Grupo de Reproducción
Organización para la Cooperación y el Desarrollo Económico (2003), indica que algunos indicadores del grupo de reproducción son los siguientes: conocimiento de hechos, representaciones de problemas comunes, reconocimiento de equivalentes, recopilación de propiedades y objetos matemáticos familiares, ejecución de procedimientos rutinarios, aplicación de destrezas técnicas y de algoritmos habituales, el manejo de expresiones con símbolos y fórmulas establecidas y realización de cálculos.
Proceso o Grupo de Conexión
Según Organización para la Cooperación y el Desarrollo Económico (2003), las competencias del grupo de conexión se apoyan en las de reproducción. Además de las competencias descritas para el grupo de reproducción, las competencias del grupo de conexión comprenden las siguientes: distinguir entre definiciones y afirmaciones, comprender y emplear conceptos matemáticos en contextos que difieren de los iniciales, seguir y evaluar el encadenamiento de los argumentos matemáticos de diferentes tipos; tener sentido de la heurística, abstraer la realidad a través de un modelo, interpretar alternando los modelos, resolver tales problemas mediante la utilización de procedimientos y aplicaciones estándar, descodificar, codificar e interpretar formas de representación familiar, seleccionar y cambiar entre diferentes formas de representación, Descodificar e interpretar el lenguaje formal y simbólico básico en situaciones desconocidas, emplear soportes y herramientas familiares en contextos, situaciones diferentes.
Proceso o Grupo de Reflexión
También, los indicadores o competencias para este grupo se tienen: distinguir entre definiciones, teoremas, conjeturas, hipótesis y afirmaciones; comprender y emplear conceptos matemáticos en contextos nuevos o complejos; comprender y tratar la amplitud y los límites de los conceptos matemáticos dados y generalizar los resultados; traducir la realidad a estructuras matemáticas en contextos complejos; Comprender y saber expresarse oralmente y por escrito sobre cuestiones matemáticas.
La Tabla 1 resulta útil para clasificar los ítems elaborados por procesos o grupos globales. Este ofrece una representación gráfica de los grupos de competencia y resume las diferencias entre ellos. Las competencias señaladas anteriormente, se pueden encontrar en los tres grupos o procesos. Según los requisitos de cada pregunta podemos asignarla al grupo de competencia.
Tabla 1 - Procesos matemáticos en la evaluación.
Fuente: Organización para la Cooperación y el Desarrollo Económico (2003).
Niveles de Competencia
En la Tabla 2 se presentan descripciones de los ocho niveles de competencia de los que trata esta investigación. Estos niveles forman la base de la escala. Las capacidades matemáticas fundamentales desempeñan un papel central en la definición de lo que significa estar en diferentes niveles de las escalas para la competencia matemática en general y para cada uno de los procesos de los que informa.
Tabla 2 - Niveles de competencia.
| Nivel | Descripción |
|---|---|
| 6 | Los alumnos saben formar conceptos, generalizar y utilizar información basada en investigaciones y modelos de situaciones problemáticas complejas, así como usar sus conocimientos en contextos relativamente no habituales. Pueden relacionar diferentes fuentes de información y representaciones y traducirlas entre ellas de manera flexible. Los estudiantes poseen un pensamiento y razonamiento matemático avanzado. Los jóvenes pueden aplicar su entendimiento, comprensión, y su dominio de operaciones y relaciones matemáticas simbólicas y formales, para desarrollar nuevos enfoques y estrategias para abordar situaciones nuevas. Además, pueden reflexionar sobre sus acciones y formular y comunicar con exactitud sus acciones y reflexiones relativas a sus descubrimientos, interpretaciones, argumentos y su adecuación a las situaciones originales. |
| 5 | En el nivel 5, los alumnos saben desarrollar modelos y trabajar con ellos en situaciones complejas, identificando los condicionantes y especificando los supuestos. Pueden seleccionar, comparar y evaluar estrategias adecuadas de solución de problemas para abordar problemas complejos relativos a estos modelos. Los alumnos pertenecientes a este nivel pueden trabajar estratégicamente utilizando habilidades de pensamiento y razonamiento bien desarrolladas, así como representaciones adecuadamente relacionadas, caracterizaciones simbólicas y formales, e intuiciones relativas a estas situaciones. Pueden reflexionar sobre sus acciones y formular y comunicar sus interpretaciones y razonamientos. |
| 4 | En el nivel 4, los alumnos pueden trabajar con eficacia con modelos explícitos en situaciones complejas y concretas que pueden conllevar condicionantes o exigir la formulación de supuestos. Pueden seleccionar e integrar diferentes representaciones, incluidas las simbólicas, asociándolas directamente a situaciones del mundo real. Los alumnos de este nivel saben utilizar su gama limitada de habilidades y razonar con cierta perspicacia en contextos sencillos. Pueden elaborar y comunicar explicaciones y argumentos basados en sus interpretaciones, argumentos y acciones. |
| 3 | En el nivel 3, los alumnos saben ejecutar procedimientos descritos con claridad, incluyendo aquellos que requieren decisiones secuenciales. Sus interpretaciones son lo bastante sólidas para fundamentar la creación de un modelo sencillo, seleccionar y aplicar estrategias de solución de problemas sencillos. En este nivel, saben interpretar y utilizar representaciones basadas en diferentes fuentes de información y razonar directamente a partir de ellas. Muestran cierta capacidad para manejar porcentajes, fracciones y números decimales, así como para trabajar con relaciones proporcionales. Sus soluciones reflejan que pueden desarrollar una interpretación y un razonamiento básicos. |
| 2 | En el nivel 2, los alumnos saben interpretar y reconocer situaciones en contextos que solo requieren una inferencia directa. Los alumnos de este nivel pueden extraer información de una única fuente y usar un único modo de representación. Los estudiantes pueden utilizar algoritmos básicos, fórmulas, procedimientos o convenciones para resolver problemas que contengan números enteros. Son capaces de hacer interpretaciones literales de los resultados. |
| 1 a | En el nivel 1a, los alumnos saben responder a preguntas relacionadas con contextos que les son conocidos, en los que está presente toda la información pertinente y las preguntas están claramente definidas. Son capaces de identificar la información y llevar a cabo procedimientos rutinarios siguiendo unas instrucciones directas en situaciones explícitas. Pueden realizar acciones obvias que se deducen inmediatamente de los estímulos presentados. |
| 1 b | En el nivel 1b, los alumnos pueden entender preguntas relacionadas con contextos que les son conocidos, que incluyen toda la información pertinente y que tienen enunciados breves y sintácticamente simples. Son capaces de seguir unas instrucciones claramente enunciadas. Pueden dar el primer paso de una solución de dos pasos a un problema. |
| 1 c | En el nivel 1c, los alumnos pueden entender preguntas relacionadas con contextos sencillos que les son conocidos, que incluyen toda la información pertinente y que tienen enunciados breves y sintácticamente simples. Son capaces de seguir una sola instrucción claramente enunciada. Pueden resolver problemas que se limiten a un único paso o cuenta. |
Fuente: Organización para la Cooperación y el Desarrollo Económico (2017).
A continuación, en la Tabla 3, se presenta la matriz de distribución de ítems, según proceso, contenido, nivel, competencia, y contexto.
Tabla 3 Matriz de distribución de las características de cada ítem.
| Pensar y Razonar | ||||
| Procesos | Ítem | Contenido | Nivel | Contexto |
| Reproducción | 1 | Conjunto de números naturales ≤ 100 | 1c | Personal |
| 2 | Relación de orden en los números naturales ≤ 100 | 1c | ||
| 3 | Valor relativo o posicional de un número natural ≤ 100. | 1b | ||
| 4 | Conteo regresivo y progresivo | 1b | Social | |
| 5 | Unidades y decenas | 1a | ||
| 6 | Unidad y sus fracciones | 2 | ||
| Conexión | 7 | Suma | 3 | Laboral |
| 8 | Resta | 4 | ||
| Reflexión | 9 | Multiplicación | 5 | |
| 10 | División | 6 | Científico | |
| Argumentación | ||||
| Reproducción | 11 | División | 1c | Personal |
| 12 | Conjunto de números naturales ≤ 100 | 1c | ||
| 13 | Relación de orden en los números naturales ≤ 100 | 1b | ||
| 14 | Valor relativo o posicional de un número natural ≤ 100. | 1b | Social | |
| 15 | Conteo regresivo y progresivo | 1a | ||
| 16 | Unidades y decenas | 2 | ||
| Conexión | 17 | Unidad y sus fracciones | 3 | Laboral |
| 18 | Suma | 4 | Científico | |
| Reflexión | 19 | Resta | 5 | |
| 20 | Multiplicación | 6 | ||
| Comunicación | ||||
| Reproducción | 21 | Multiplicación | 1c | Personal |
| 22 | División | 1c | ||
| 23 | Conjunto de números naturales ≤ 100 | 1b | ||
| 24 | Relación de orden en los números naturales ≤ 100 | 1b | Social | |
| 25 | Valor relativo o posicional de un número natural ≤ 100. | 1a | Laboral | |
| 26 | Conteo regresivo y progresivo | 2 | ||
| Conexión | 27 | Unidades y decenas | 3 | |
| 28 | Unidad y sus fracciones | 4 | Científico | |
| Reflexión | 29 | Suma | 5 | |
| 30 | Resta | 6 | ||
| Construcción de modelos | ||||
| Reproducción | 31 | Resta | 1c | Personal |
| 32 | Multiplicación | 1c | Social | |
| 33 | División | 1b | ||
| 34 | Conjunto de números naturales ≤ 100 | 1b | ||
| 35 | Relación de orden en los números naturales ≤ 100 | 1a | Laboral | |
| 36 | Valor relativo o posicional de un número natural ≤ 100. | 2 | ||
| Conexión | 37 | Conteo regresivo y progresivo | 3 | |
| 38 | Unidades y decenas | 4 | Científico | |
| Reflexión | 39 | Unidad y sus fracciones | 5 | |
| 40 | Suma | 6 | ||
| Formulación y resolución de problemas | ||||
| Reproducción | 41 | Suma | 1c | Personal |
| 42 | Resta | 1c | ||
| 43 | Multiplicación | 1b | ||
| 44 | División | 1b | Social | |
| 45 | Conjunto de números naturales ≤ 100 | 1a | ||
| 46 | Relación de orden en los números naturales ≤ 100 | 2 | ||
| Conexión | 47 | Valor relativo o posicional de un número natural ≤ 100. | 3 | Laboral |
| 48 | Conteo regresivo y progresivo | 4 | ||
| Reflexión | 49 | Unidades y decenas | 5 | |
| 50 | Unidad y sus fracciones | 6 | Científico | |
| Empleo de Soporte y Herramientas | ||||
| Reproducción | 71 | Conteo regresivo y progresivo | 1c | Personal |
| 72 | Unidades y decenas | 1c | Social | |
| 73 | Unidad y sus fracciones | 1b | ||
| 74 | Suma | 1b | ||
| 75 | Resta | 1a | Laboral | |
| 76 | Multiplicación | 2 | ||
| Conexión | 77 | División | 3 | |
| 78 | Conjunto de números naturales ≤ 100 | 4 | Científico | |
| Reflexión | 79 | Relación de orden en los números naturales ≤ 100 | 5 | |
| 80 | Valor relativo o posicional de un número natural ≤ 100. | 6 | ||
| Empleo de operaciones y de un lenguaje simbólico, formal y técnico | ||||
| Reproducción | 51 | Unidades y decenas | 1c | Personal |
| 52 | Unidad y sus fracciones | 1c | ||
| 53 | Suma | 1b | ||
| 54 | Resta | 1b | Social | |
| 55 | Multiplicación | 1a | Laboral | |
| 56 | División | 2 | ||
| Conexión | 57 | Conjunto de números naturales ≤ 100 | 3 | |
| 58 | Relación de orden en los números naturales ≤ 100 | 4 | Científico | |
| Reflexión | 59 | Valor relativo o posicional de un número natural ≤ 100. | 5 | |
| 60 | Conteo regresivo y progresivo | 6 | ||
| Representación | ||||
| Reproducción | 61 | Unidad y sus fracciones | 1c | Personal |
| 62 | Suma | 1c | ||
| 63 | Resta | 1b | ||
| 64 | Multiplicación | 1b | Social | |
| 65 | División | 1a | ||
| 66 | Conjunto de números naturales ≤ 100 | 2 | ||
| Conexión | 67 | Relación de orden en los números naturales ≤ 100 | 3 | Laboral |
| 68 | Valor relativo o posicional de un número natural ≤ 100. | 4 | Científico | |
| Reflexión | 69 | Conteo regresivo y progresivo | 5 | |
| 70 | Unidades y decenas | 6 | ||
Segunda etapa
Una vez elaborado el instrumento de medición, se procedió a obtener la validez del mismo a través de una entrevista a un grupo de docentes con experiencia en el tema con grado de maestría y doctorado, quienes evaluaron de manera individual todos los ítems del cuestionario. Este panel estuvo compuesto por siete profesores: 4 profesores a nivel universitario, dos maestros de escuela primaria, y un psicólogo. Esta etapa es importante debido a que se obtiene evidencia de que las competencias matemáticas a evaluar están correctamente representadas en los ítems formulados.
Como investigadores queremos que nuestro instrumento tenga la propiedad de medir y observar si los estudiantes cuentan con las capacidades y habilidades para resolver problemas aritméticos en contexto real. Para ello, al panel se le presentó un ejemplar de la prueba y el instrumento. El panel de expertos analizó cada ítem según tres categorías: Esencial, Útil / No esencial, y No necesario. Posteriormente, se procedió a determinar el número de coincidencias en la categoría “Esencial”. Para que cada ítem sea considerado válido debe contar con más del 57% de acuerdo entre los jueces.
Se procedió a evaluar la validez de contenido a través de la fórmula de Lawshe (1975):
Y con la fórmula de Tristán (2008), que modifica la fórmula de Lawshe, esta es,
Para que un ítem sea aprobado el CVR debe ser superior a 29, por el número de panelistas que tenemos, mientras que con CVR´ debe ser superior a 0.5823. El instrumento final quedó validado con un nivel de 0.88, lo cual es muy satisfactorio, puesto que está por encima de 0.58. Cabe destacar que, esto está sujeto a la experiencia de los expertos que asignaron una serie de valores a los ítems, así como a las variables e indicadores del cuestionario.
Tomando en consideración los valores y observaciones del Juicio de expertos, se obtuvo el instrumento resultante, eliminando los ítems que según Tristán y Lawshe no son adecuados para el instrumento. Por lo que, el instrumento contiene un total de 28 ítems, distribuidos como se muestra en la Tabla 4.
Tabla 4 - Ítems por competencia del instrumento validado.
| Competencia | Ítems | Total |
|---|---|---|
| Pensar y razonar | 1,3,,5,7,9 | 5 |
| Argumentación | 11,15,17,19 | 4 |
| Comunicación | 23,24,27,29 | 4 |
| Construcción de modelos | 31,33,36,38 | 4 |
| Formulación y resolución de problemas | 43,44,47,50 | 4 |
| Empleo de operaciones y de un lenguaje simbólico, formal y técnico | 53,57,60 | 3 |
| Representación | 62,67,70 | 3 |
| Empleo de soporte y herramientas | 80 | 1 |
Tercera Etapa
Una vez recolectado los datos se iniciará el proceso para obtener la información que permita cumplir con los objetivos propuestos. Para el tratamiento y análisis de los datos se hará un análisis factorial exploratorio (AFE) mediante el software Statics Package for the Social Sciences versión 22 para Windows. La caracterización de las variables se realizará mediante medidas descriptivas, como la media (para variables cuantitativas) y porcentajes (para variables cualitativas). Los resultados se presentarán mediante Tabla s y/o gráficos. De esta manera, se determinará el grado en que los ítems y componentes del instrumento forman el constructo que se desea medir. Para lo anterior, se seleccionará 21 escuelas de la provincia de Coclé y se les aplicará la prueba piloto, obtenida en la etapa anterior. Los estudiantes desarrollarán el cuestionario individual y auto administradamente.
Cuarto Etapa
En la etapa final, de este proceso de validación del instrumento de medición, se realizará un análisis de consistencia interna a través del Alfa de Cronbach, con el propósito de establecer la medida en la cual las competencias matemáticas están presentes en cada uno de los ítems y el grado en que se correlacionan entre sí.
Resultados y discusión
En el estudio se ha obtenido un instrumento aprobado con un índice de 0.88, considerado por los expertos como satisfactorio. Además, por primera vez en Panamá se cuenta con un Instrumento para evaluar ocho competencias cognitivas en el área de la Aritmética en primer grado primaria. También, se ha elaborado un instrumento cónsono con las teorías de aprendizaje y que es capaz de medir el contenido curricular del Ministerio de Educación para el primer grado primaria. Finalmente, el instrumento mide los conocimientos en los contextos personal, laboral, público y científico.
Conclusiones
El alto índice de fracasos en matemática a nivel primario, y el bajo rendimiento en los niveles siguientes, inclusive el universitario, nos sugiere la necesidad de aplicar un instrumento para determinar, de manera científica, si los estudiantes del primer grado de la escuela primaria cuentan con las competencias para resolver y aplicar conceptos básicos de la aritmética en la solución de problemas reales.
Los problemas de matemática a nivel de Olimpiadas en el sector primario nos indica que nuestros estudiantes deben ser preparados y capacitados en la solución de problemas de aritmética aplicados a la vida real, por lo cual es necesario determinar a través de un instrumento, si nuestros estudiantes pueden presentar un buen desempeño en este tipo de actividades.
Las continuas inversiones del gobierno en el mejoramiento de la calidad de la educación nos sugieren una continua evaluación del desempeño del estudiante en cada una de las áreas del saber matemático, en especial la Aritmética, a través de la aplicación de instrumentos de validación.