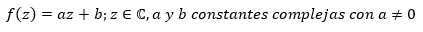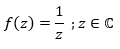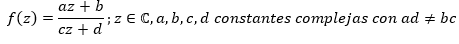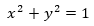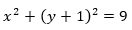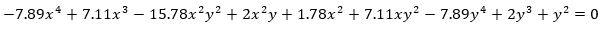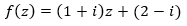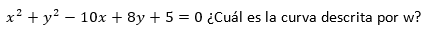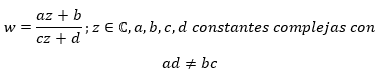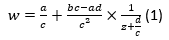Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
A diferencia de las funciones reales de variable real cuya representación gráfica resulta relativamente fácil en el plano xy, cuando las variables son complejas su representación gráfica es más complicada porque si w = f(z) es una función de variable compleja, a cada punto (x, y) del plano z, mediante f (x+ iy) se obtiene un punto (u, v) del plano w donde w = u + vi, de modo que f transforma puntos del plano z en puntos del plano w, por eso una solución sería usar planos separados para cada variable.
A esta correspondencia entre los puntos situados en dos planos se llama transformación o representación del plano z en puntos del plano w mediante la función f(z); pero aun cuando se use planos separados para representar a w y a z, generalmente resulta conveniente realizar tales representaciones como si fuera realizada en el mismo plano, esto se logra mediante transformaciones gráficas tales como la traslación o la rotación.
Siguiendo esta idea es importante estudiar las transformaciones que producen determinadas funciones a una región determinada del plano, tales son los casos de las funciones:
Las transformaciones realizadas por estas funciones sobre una región del plano, tiene fundamentaciones matemáticas que indudablemente requieren de estudios de la teoría de la variable compleja, pero como se dijo, “esto se logra mediante transformaciones gráficas tales como la traslación o la rotación” y este es el propósito del trabajo que presentamos, con la particularidad de que tales transformaciones se harán utilizando el asistente matemático GeoGebra; como medio auxiliar heurístico para comprender los procederes matemáticos que permiten tales transformaciones.
Desarrollo
En la introducción se hizo referencia a los medios auxiliares heurísticos, para Crespo Hurtado, (2007), “los medios auxiliares heurísticos son todos aquellos elementos que sirven de soporte material a la resolución de un problema y facilitan la aplicación de las reglas, principios y estrategias heurísticas… la computadora, con la revolución que impregna a todos los procesos donde se inserta, redimensiona estos medios convirtiéndose en un eficiente apoyo a alumnos y profesores en la resolución de problemas… haciendo uso de asistentes matemáticos, agrupados generalmente en los que permiten: El procesamiento algebraico, el tratamiento de funciones con el graficado de las mismas y el trabajo con conjuntos numéricos, matrices, polinomios, vectores, etc., mediante un sistema de herramientas interactivas con las que pueden realizarse diferentes cálculos de un alto nivel de complejidad. Estos softwares tienen como finalidad facilitar a distintos profesionales el engorroso cálculo matemático, sin interés del proceso de enseñanza-aprendizaje de la Matemática”.
Por otro lado, GeoGebra es un software matemático interactivo libre para la educación en colegios y universidades que en la actualidad tiene versiones para tecnología celular lo que facilita su aplicación en países en vías de desarrollo (Hohenwarter, 2009; Toto & Crespo Borges, 2016; Toto, 2019).
Entre sus posibilidades es básicamente un procesador geométrico y un procesador algebraico, es decir, un compendio de matemática con software interactivo que reúne geometría, álgebra, estadística y cálculo, permitiendo el trazado dinámico de construcciones geométricas de todo tipo así como la representación gráfica, el tratamiento algebraico y el cálculo de funciones reales de variable real, sus derivadas, integrales, etc.
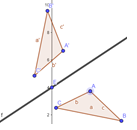
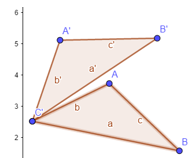
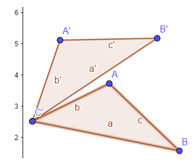
Fig. 1 - Transformación del triángulo ABC en A’B’C’ mediante la simetría axial alrededor de la recta f.
Bajo esta concepción de utilizar el GeoGebra como medio auxiliar heurístico se presentará el estudio de las principales transformaciones conformes elementales (Figura 1).
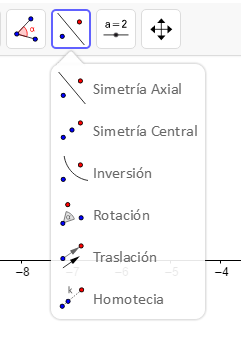
En la imagen adjunta se muestran las posibilidades que ofrece GeoGebra para realizar transformaciones gráficas de regiones del plano, las cuales satisfacen las necesidades para realizar transformaciones conformes y son consideradas sus transformaciones base. (Figura 2).
La simetría axial (también llamada rotacional, radial o cilíndrica) es la simetría alrededor de un eje. Un sistema tiene simetría axial o axisimetría cuando todos los semiplanos tomados a partir de cierta mediatriz y conteniéndolo presentan idénticas características. En la gráfica adjunta se muestra la transformación del triángulo ABC en A’B’C’ mediante la simetría axial alrededor de la recta f tomada como eje de simetría.
La simetría central, es la simetría respecto de un punto de vista y "los puntos correspondientes". En una simetría central, los segmentos homólogos son iguales y la medida de los ángulos correspondientes también son iguales.
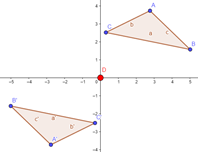
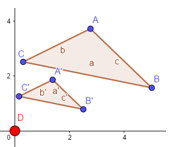
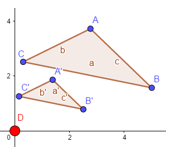
En la gráfica adjunta se muestra la transformación del triángulo ABC en A’B’C’ mediante la simetría central respecto al origen de coordenadas (Figura 3).
Inversión, Invierte un objeto en una circunferencia. Debe seleccionarse un objeto y la circunferencia donde se reflejará en cualquier orden. Para el caso de transformaciones en el plano complejo la circunferencia debe estar centrada en el origen y radio unidad, es decir, según la ecuación
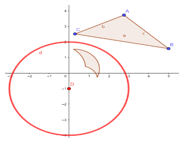
Fig. 4 - Transformación del triángulo ABC mediante la inversión en este caso para mejor visualidad se ha empleado una circunferencia.
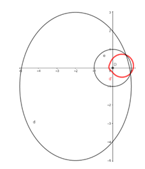
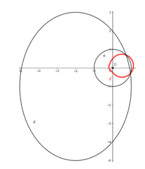
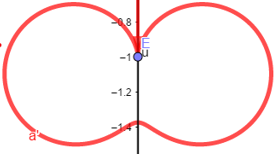
En la Figura 4 se muestra la transformación del triángulo ABC mediante la inversión en este caso para mejor visualidad se ha empleado la circunferencia de centro en (0, -1) y radio de longitud 3,
Cuando se invierte una gráfica con su correspondiente ecuación, GeoGebra devuelve no solo la imagen de la gráfica, también da la ecuación de la figura invertida sobre la circunferencia en cuestión, ejemplo:
Para la elipse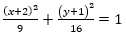 
se obtiene, sobre la circunferencia 
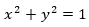la curva que aparece bordeada en rojo en la gráfica, cuya ecuación es:
Rotación es el movimiento de cambio de orientación de un cuerpo o un sistema de referencia de forma que una línea (llamada eje de rotación) o
un punto permanece fijo (Figura 5).
La Figura 6 muestra la transformación del triángulo ABC en A’B’C’ mediante una rotación de 450 en sentido antihorario alrededor del punto C.
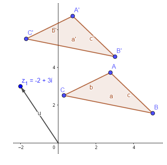
Fig. 6 - Transformación del triángulo ABC en A’B’C’ mediante una rotación de 450 en sentido antihorario alrededor del punto C.
Una traslación es una isometría en el espacio euclídeo caracterizada por un vector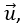 
, tal que, a cada punto P de un objeto o figura se le hace corresponder otro punto P', tal que:
La Figura 7 muestra la traslación del triángulo ABC hasta A’B’C’ según el vector 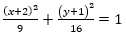módulo del número complejo
Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor.
En la Figura 8 se muestra una homotecia con centro en el origen de coordenadas que reduce a la mitad al triángulo ABC.
Transformación lineal
Se denomina transformación lineal toda transformación del plano que se realiza mediante la función
La teoría indica que esta transformación es conforme en todo el plano porque para cualquier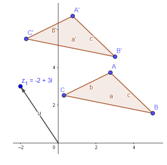 
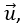entonces, la imagen de cualquier z del plano z es el punto se transforma por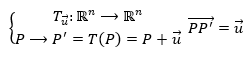
Si se analiza la primera parte de la expresión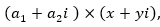 
, se tiene expresando en forma exponencial se tiene:
De lo anterior se tiene:
Continuando el análisis se tiene:
Conclusión:
Una transformación lineal de cualquier parte del plano z al plano w se logra mediante el siguiente algoritmo:
Realizar una homotecia de factor P a de la región z del plano.
Rotar un ángulo ϕ la parte del plano resultante de (1)
Trasladar (2) según el vector P b
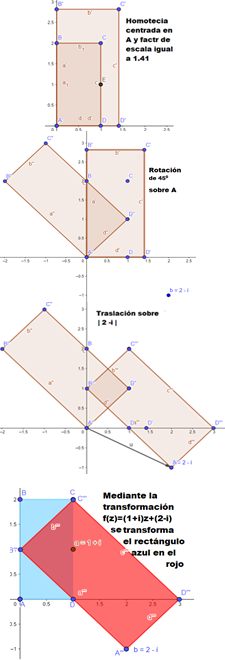
Ejemplo 1: Transformar el rectángulo cuyos vértices son 0,0 ; 0,2 ; 1,2 ;(1,0) mediante la función
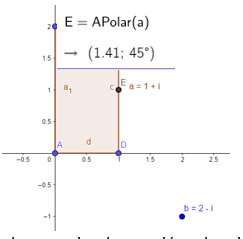
Los valores ( ρ 𝑎 , 𝜑) para la homotecia y la rotación, se obtienen mediante el comando GeoGebra (Figura 9).
Seguidamente se tiene la secuencia de pasos del algoritmo antes descrito como se muestra en la sucesión de imágenes que se muestra a continuación (Figura 10):
Transformación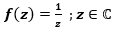 
(Figura 11)
Esta transformación está implementada en GeoGebra por eso un problema cuya solución requiere de esta transformación tiene una fácil solución con GeoGebra, tal es el caso del siguiente problema tomado de un texto de variable compleja:
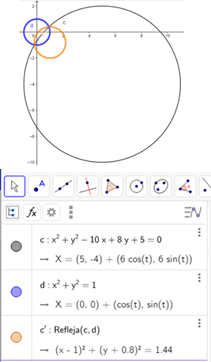
Ejemplo 2: Sea 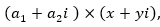y sea z un círculo que no pasa por el origen de ecuación
La respuesta aparece en las imágenes adjuntas:
Transformación homográfica: se denomina homografía a toda transformación proyectiva que determina una correspondencia entre dos figuras geométricas planas, de forma que a cada uno de los puntos y las rectas de una de ellas le corresponden, respectivamente, un punto y una recta de la otra. También se denominan transformaciones lineales fraccionaras o transformaciones bilineales y son transformaciones de la forma
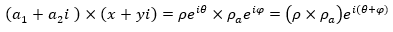expresión que se corresponde con la transformación lineal expuesta anteriormente.
Si se transforma en:
Esta transformación puede ser descrita por la siguiente sucesión de transformaciones elementales:
Siguiendo este algoritmo, en forma análoga a como se procedió con ejemplo 1, es posible comprobar que la curva descrita por la transformación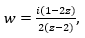
, cuando z recorre la parábola 
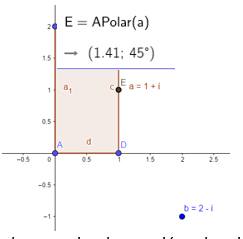es la curva que se adjunta (Figura 12):
Conclusiones
En la alternativa propuesta se destacan, el equilibrio entre el cálculo algebraico y la representación gráfica de los resultados.
Se muestra cómo a partir de una sucesión de transformaciones elementales implementadas en el GeoGebra es posible no sólo encontrar la representación gráfica de la curva resultante de una transformación conforme, también es posible determinar la ecuación de dicha curva.
