Introducción
Las formas de estructuración sistémica de los contenidos curriculares más difundidas en la literatura consultada por los autores de este trabajo son la genética y la estructural - funcional. La primera permite determinar un objeto singular, a partir del cual se generan los restantes elementos que conforman un estudio o una teoría; se destacan en ello N. Sálmina (1984) y H. Hernández (1989). Esta estructura elemental es la conocida como célula generadora. La forma estructural funcional presenta el objeto de estudio como una invariante que en dependencia de las particularidades y especificidades que lo complementen integrará un nuevo objeto del conocimiento.
Ambos tipos de estructuraciones pueden concebirse para el diseño de los contenidos, lo cual posibilita el logro de elevados índices de reflexión, generalización y solidez, así como la aparición de operaciones lógicas del pensamiento tales como el análisis, la síntesis y la abstracción, según se ha demostrado en investigaciones como las de R. Delgado (1999) y P. Beltrán (2008).
Existen otras formas de estructuraciones sistémicas tales como los ejes temáticos, los nodos cognitivos y la resolución de clases de problemas. Estas dos últimas formas de estructurar sistémicamente el contenido han sido aplicadas en el área de las matemáticas.
Los ejes temáticos, según M. de la Rúa, (2000) son el punto de vista particular y/o coyuntural que permite el tránsito ordenado entre los temas específicos que participan en el análisis de un problema o contenido particular y han sido utilizados en las ciencias sociales.
Según H. Hernández (1995) y T. Diez (2003) los nodos cognitivos permiten graficar el conocimiento estructurado como una red n-dimensional de nodos, cada uno de los cuales constituye un punto de acumulación de información en torno a un concepto o una habilidad. Esta forma de estructurar el contenido constituye un recurso metodológico, que facilita la organización del pensamiento del estudiante, al posibilitar que pueda activar selectivamente la información necesaria para resolver un determinado problema.
En el caso de la resolución de clases de problemas variando los instrumentos de solución, es un nuevo tipo de enfoque sistémico, en el que no aparecen estructuras funcionales (invariante, célula) a partir de las cuales se desarrolla el sistema. En esta variante de estructuración de contenidos, según R. Delgado (1999), cada clase de problemas se corresponde con una habilidad general de la matemática específica y cada tema de la disciplina brinda nuevos instrumentos de solución para cada una de las clases de problemas.
Se asume en este trabajo la forma de estructuración de tipo estructural - funcional pues en ella se presenta el objeto de estudio como una invariante que en dependencia de las particularidades y especificidades que lo complementen integrará un nuevo objeto del conocimiento.
La invariante es un concepto de orden superior respecto a una relativa amplia gama de conceptos subordinados que pudieran considerarse como casos particulares suyos, en el marco de un sistema estructural-funcional de contenidos, en tanto él representa una estructura estable (dentro de los límites del sistema), cuyas componentes al variar, permiten la deducción de dichos conceptos subordinados. (Delgado, 1999, p.34)
Según Z. Reshetova (1988) y N. Talizina (1988) la invariante, es cualquier estructura de varios componentes, que están presentes y de forma estable en una multitud de casos particulares que son consideradas como sus variantes.
El término invariante ha sido utilizado por diferentes investigadores. Algunos como H. Hernández (1989); J. López (2016); T. Rodríguez (1991), hablan de invariante de conocimiento y otros como J. Arce (2009), A. Pérez (2015), N. Blanco (2016) de invariante de habilidad. Se concuerda con E. Regalado (2008) quien considera que las invariantes de conocimiento deben acompañarse de las invariantes de la habilidad y de esta forma permitir una mejor comprensión por parte del educando y una mayor posibilidad de aplicación de los conocimientos adquiridos en la práctica.
H. Fuentes (1997) plantea que la invariante de habilidad se define como el contenido lógico del modo de actuación del profesional y como una generalización esencial de las habilidades que tiene su concreción en cada disciplina.
Se asume esta definición ya que a partir de ella se deduce que usar AM, visto como una invariante de habilidad incluye además contenidos generalizados que se concretan en la disciplina MS y en su relación estrecha con habilidades específicas de la matemática. (Cruz, 2001) Por otro lado, se considera que esta invariante de habilidad contribuye a la formación de la personalidad a través de valores y motivaciones propias de la profesión. Según J. Arce (2009) las invariantes de habilidad constituyen el mayor nivel de sistematicidad del proceso docente-educativo (niveles: carrera y disciplina), al estar formadas por habilidades generalizadas que en su propia integración revelan el modo de actuación del profesional.
De acuerdo con las ideas anteriores, se define en este trabajo a la estructuración sistémica de los contenidos de la disciplina MS, como la acción encaminada a establecer un modelo o esquema que exprese la secuencia lógica, interrelación, agrupación o distribución de los conceptos, leyes, teorías, procedimientos algorítmicos, heurísticos, habilidades y valores a desarrollar en la disciplina MS, a partir de su interacción con la invariante de habilidad usar asistentes matemáticos vinculada a la resolución de problemas intra y extramatemáticos, para dar cumplimiento a los objetivos declarados en el programa de estudio de dicha disciplina.
Desarrollo
En el modelo de actuación para la formación del ingeniero radioelectrónico de las Instituciones Docentes de Nivel Superior (IDNS) de las Fuerzas Armadas Revolucionarias (FAR) se plantean objetivos generales y específicos asociados al uso de recursos tecnológicos para resolver determinados problemas en el ejercicio de su profesión. El plan de estudio de esta carrera debe tener en cuenta estos propósitos, al emplear en las disciplinas que lo conforman, simuladores y AM como el Matlab y el Mathcad, que de forma automatizada realizan los cálculos matemáticos necesarios en las asignaturas de ciencias básicas generales y específicas.
Por lo antes expuesto es preciso que desde el currículo se propicie en el programa de la disciplina MS, el uso de los AM, con lo cual se condiciona que el mismo no se realice de forma espontánea, permitiéndole a los educandos, apropiarse de sus potencialidades desde los primeros años de las carreras de ingeniería.
Durante esta etapa de formación se imparten 11 temas que tienen en cuenta los contenidos específicos y no específicos de la propia disciplina, los cuales se encuentran distribuidos en un total de 300 horas. Los temas que se reflejan en el programa de estudio de la disciplina MS para la formación del ingeniero radioelectrónico de las IDNS de las FAR, permiten definir un esquema orientador sistémico de dicha disciplina. Entre los propósitos fundamentales de dicho programa, se encuentran aquellos que están relacionados con la formación y desarrollo de habilidades con el uso de las tecnologías de la información y las comunicaciones y de manera particular con el uso de AM.
La habilidad usar asistentes matemáticos es definida por los autores del presente trabajo como el dominio de un conjunto de acciones conceptuales, traductoras, operativas, heurísticas y metacognitivas; mediante el manejo de softwares profesionales para el procesamiento de datos y el cálculo simbólico, numérico y gráfico de expresiones matemáticas, con el propósito de solucionar problemas intra o extramatemáticos.
Se definen como acciones de dicha habilidad conceptualizar, traducir, operar y solucionar. En la primera acción, el educando identifica al AM capaz de resolver el problema. Esta operación debe realizarse siempre a la hora de usar un AM en los temas declarados en el programa de estudio de la disciplina MS, razón por la cual se muestra con un asterisco en la figura que se muestra en el anexo 1. Posteriormente se define, mediante una lectura detallada de la situación planteada, qué teorías y técnicas matemáticas utilizar a partir de la comparación de reglas, algoritmos, conceptos y la comprobación lógica de leyes y teoremas.
La acción correspondiente a la traducción, permite interpretar los conceptos necesarios para resolver el problema a partir de la modelación de estrategias y la recodificación de símbolos y comandos propios del AM. La revisión de la ayuda del AM, en caso que sea necesario y la indagación de tutoriales que orienten al educando en este sentido puede ejecutarse en todos los temas de la disciplina por lo cual se señala también con un asterisco en la figura que se muestra en el anexo 1.
Realizar representaciones gráficas, cálculos y aproximaciones vinculadas al problema que se desea resolver con el AM, mediante algoritmos ejecutados a través de la optimización de estrategias, permite resolver el problema a partir del método planteado y realizar conjeturas que posibiliten la debida interpretación de los resultados obtenidos con la ayuda del AM, a través de técnicas de control y autocontrol.
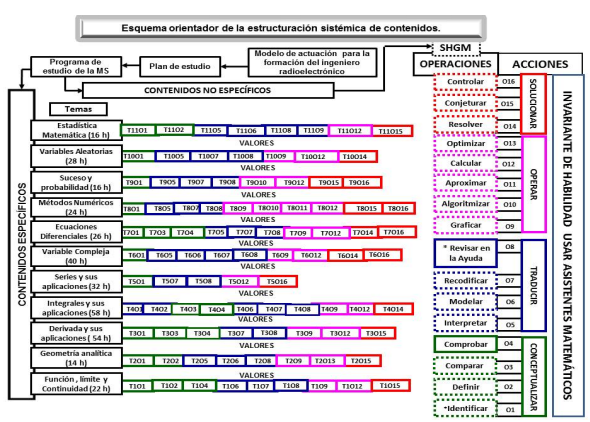
En el presente trabajo se propone establecer una relación sistémica entre cada uno de estos temas y las operaciones que conforman a las acciones conceptualizar, traducir, operar y solucionar de la habilidad usar asistentes matemáticos, las cuales se muestran en el esquema de la figura1 (anexo 1) con recuadros de color verde, azul, morado y rojo respectivamente. Dichas operaciones guardan una estrecha relación con el sistema de habilidades generales de la Matemática declarado por el grupo β de Matemática Educativa (H. Hernández (1999)), las cuales se muestran en la figura 1 en recuadros con líneas discontinuas.
Las reflexiones anteriores posibilitan una ampliación del sistema de habilidades del programa de la disciplina MS al establecer una relación entre los temas de la disciplina y las operaciones que conforman a la habilidad usar asistentes matemáticos, identificadas en el esquema de la figura 1 con el color de la acción correspondiente.
Para expresar el sistema de habilidades declaradas en el programa de estudio de la disciplina MS en cada uno de los temas, se tendrá en cuenta el objetivo que se pretende alcanzar, a partir de su vínculo con las acciones conceptuales, traductoras, operativas, heurísticas y metacognitivas que conforman a la habilidad usar asistentes matemáticos declarada con anterioridad y el nivel a alcanzar, el cual está relacionado con la resolución de problemas intra y extramatemáticos mediante el uso de AM.
En un sistema debe tenerse en consideración una agrupación de elementos en interacción dinámica organizados en función de un objetivo, se sugiere en este trabajo, estructurar los contenidos de la disciplina MS de forma de forma tal que los mismos y las operaciones que conforman a la habilidad “usar asistentes matemáticos” formen un todo único a partir de las relaciones que se establecen entre cada uno de ellos.
La propuesta de estructuración sistémica de contenidos matemáticos que brinda este trabajo, tiene como objetivo organizar los contenidos tomando como eje transversal la invariante de habilidad usar asistentes matemáticos, para lograr la integración de los mismos al currículo de la disciplina MS.
Resultados y discusión
Las relaciones que se establecen entre estos contenidos y las operaciones que conforman la habilidad usar asistentes matemáticos, determinan la forma, el orden y la jerarquía de cada uno de los componentes dentro del sistema, lo cual pone de manifiesto la lógica de la estructuración sistémica estructural funcional que se propone.
En la figura 1 (anexo 1) se muestra un esquema orientador sistémico de la disciplina MS para la formación del ingeniero radioelectrónico que evidencia la relación sistémica existente entre los temas de la disciplina y las operaciones que conforman a la habilidad usar asistentes matemáticos.
Para un mejor entendimiento del mismo, al tomar como ejemplo el tema 1, de acuerdo a lo planteado con anterioridad, T1O1 significa que en este tema se plantearán en el programa de estudio de la disciplina MS, objetivos del Tema 1 vinculados a la operación O1 que conforma a la habilidad usar asistentes matemáticos, la cual está relacionada con la identificación del asistente matemático capaz de resolver algunos de los problemas planteados en este tema.
Las relaciones que se muestran en el esquema, no son las únicas, pues estas dependen del objetivo que se pretende alcanzar y del contenido específico de la matemática. En el esquema aparecen aquellas que más se potencian. Es de resaltar que la formación de valores como la independencia y el compañerismo son elementos claves en este proceso y permiten el desarrollo del pensamiento lógico de los educandos.
A continuación, se muestra un ejemplo de cómo se pueden estructurar sistémicamente los contenidos de tres temas que se imparten en la disciplina MS al considerar como invariante a la habilidad usar asistentes matemáticos.
Tema “Funciones, límite y continuidad”
En este tema se hace necesario identificar aquellos AM que permiten graficar funciones elementales conocidas por el educando tales como las lineales, cuadráticas, exponenciales, logarítmicas y trigonométricas. Los AM Derive, Geogebra, Matlab y Maple son los más recomendables en este sentido.
Para representar gráficamente funciones en una y varias variables es necesario recodificar las ecuaciones correspondientes a las mismas, a partir del conocimiento y manejo de los símbolos utilizados por el AM, propiciándose la utilización de operaciones traductoras. Mediante la representación gráfica con AM se realizan construcciones más precisas y dinámicas lo cual permite que los puntos principales de las funciones puedan visualizarse en el plano coordenado, y conservar sus propiedades fundamentales.
Estas bondades del AM posibilitan el análisis de propiedades y características de las funciones y constituyen una alternativa para la interpretación gráfica, sistematización y profundización de conceptos tales como: dominio, imagen, ceros de una función, y periodicidad de funciones trigonométricas. La graficación con AM posibilita un mejor diseño de circuitos vinculados al trabajo con medios radioelectrónicos.
Los resultados obtenidos al representar funciones con AM permiten la elaboración de vías y procedimientos más efectivos para el procesamiento, e intercambio de información, de esta forma, se pueden realizar conjeturas y generalizaciones de una forma clara y lógica. El concepto de límite, está claramente asociado al de función, tanto desde el punto de vista analítico como geométrico. Ambos contenidos específicos, al ser componentes del sistema interactúan con las operaciones que conforman a la habilidad usar asistentes matemáticos a partir del cálculo, la interpretación y la representación gráfica. La imagen de un punto es otro de los conceptos que se utiliza para vincular, desde el punto de vista práctico, la existencia del límite. Al identificar a los AM que permiten calcular límites de funciones en una y varias variables, se necesita definir aquellos conceptos, leyes, teoremas y algoritmos matemáticos que permiten calcular dichos límites. Resaltan en este sentido los límites que conducen a indeterminaciones, infinitos e infinitésimos, la aplicación de la Regla de Leibnitz y la utilización de los límites fundamentales trigonométrico y algebraico.
A través del AM los educandos adquieren una idea intuitiva sobre dichos conceptos y comprueban las soluciones obtenidas a mano de los cálculos de límites realizados. Recodificar las expresiones que permiten la aplicación de los mismos en la resolución de ejercicios, constituye una operación que permitirá crear estrategias para calcular límites con el uso de AM. Desde las primeras clases prácticas de este tema se realiza el cálculo de límites de funciones en una y varias variables, lo cual se torna menos engorroso al calcular mediante algoritmos programados y la utilización de las funciones y comandos del propio AM.
El análisis de la continuidad de una función y la existencia o no del límite de la función en un punto, depende del cálculo de los límites laterales. Su interpretación gráfica se realiza mediante un AM, al visualizar el comportamiento de la función alrededor de valores extremos, los cuales, por la complejidad del cálculo, en ocasiones, no son posibles analizar de forma manual. Modelar estrategias que permitan analizar la continuidad de una función alrededor de un punto a partir de las posibilidades que brindan los AM, permite que el educando se apropie de conceptos tales como ceros del denominador y asíntotas verticales y brindar ideas intuitivas sobre los límites infinitos.
Tema “Derivada y sus aplicaciones
A partir de los conocimientos adquiridos por los educandos en el tema anterior sobre las funciones en una y varias variables, el tema “Derivada y sus aplicaciones” se introduce en la disciplina mediante problemas que conducen al concepto de derivada. Su interpretación geométrica se realiza a través del uso de algunos de los AM identificados como capaces de representar las funciones analizadas en dicho tema. Obtener la aproximación lineal o aproximación por la recta tangente de la función cuando x está cerca del punto de tangencia y visualizar dicha aproximación al usar un asistente matemático, permite un mejor entendimiento de este concepto.
El Derive, el Matlab, el Maple y el Geogebra no solo permiten realizar dicha representación, sino que, a partir de la recodificación y el manejo de símbolos, permiten calcular derivadas de funciones en una y varias variables mediante algoritmos programados y la utilización de las funciones y comandos del propio AM.
La comprobación de las soluciones obtenidas a mano al calcular derivadas de funciones en una y varias variables, se realiza de manera eficiente al usar un AM. Es necesario definir reglas, algoritmos y conceptos relacionados con el cálculo diferencial, y después de realizar una comparación entre ellos, seleccionar adecuadamente los que permiten calcular derivadas con AM de manera apropiada. En este sentido resaltan las reglas de derivación, y la regla de la cadena como vías para calcular la derivada de funciones compuestas. En este tema se presentan problemas de optimización donde las derivadas son necesarias en la determinación de los extremos locales. La interpretación de la solución obtenida al resolver los problemas planteados, permite realizar conjeturas a través de inferencias y generalizaciones y comunicar los resultados obtenidos al calcular derivadas con un AM. El trazado de curvas con AM permite a través de la representación gráfica la visualización de conocimientos asimilados en los temas anteriores. A partir del gráfico de una función de una variable real, se analiza el dominio, la imagen, los interceptos con los ejes coordenados, las asíntotas, la monotonía, y otros contenidos tratados en este tema como la existencia o no de extremos, que requieren del cálculo de la primera derivada, y el análisis de la concavidad y los puntos de inflexión con el cálculo de la segunda derivada.
La lógica aplicada en la estructuración sistémica propuesta, permite organizar el estudio de las funciones de variable real a partir del análisis de su dominio, imagen, representación gráfica, cálculo de límite, derivada e integrales y otros contenidos específicos de la disciplina MS, lo cual permite revelar la relación sistémica existente entre cada uno de los niveles jerárquicos del contenido matemático, llegar a conjeturas, así como solucionar y resolver problemas afines al próximo tema.
Tema “Variable Compleja”
Las habilidades desarrolladas por el educando en cuanto a la representación gráfica de funciones en una y varias variables y los contenidos de la enseñanza precedente, son tomadas como punto de partida en este tema. Se identifican a los AM Derive, Matlab y Geogebra como capaces de realizar operaciones con números complejos y representar gráficamente regiones del plano complejo. Los conceptos necesarios para representar regiones del plano complejo y transformar dichas regiones, están relacionados con la representación gráfica de funciones en una y varias variables, de ahí la importancia de modelar estrategias a partir de las posibilidades que brindan el AM. La recodificación de las expresiones que definen las regiones del plano complejo y los movimientos de homotecia, rotación, traslación e inversión que se efectúan al realizar una transformación bilineal, debe realizarse de forma estratégica para poder interpretar la información brindada por el AM. Otro contenido tratado en este tema es el de la transformada de Laplace, el cual puede ser visto a partir de una integral impropia resuelta con un AM, al identificar aquellos que posibilitan el cálculo de la transformada de Laplace directa e inversa de expresiones algebraicas.
De manera general, cada tema de la disciplina MS conforma un subsistema en el cual se describen como elementos en interacción dinámica, el sistema de conocimientos declarado en el programa de estudio de la disciplina y las operaciones que conforman a la habilidad usar asistentes matemáticos. La condición de sistema que adopta este proceso de estructuración de contenidos, posibilita una compresión global de dichas operaciones que permite identificar las potencialidades de los AM e interpretar y jerarquizar el papel de las interacciones que se producen entre cada uno de los temas.
Conclusiones
La estructuración sistémica de los contenidos que se propone, permite visualizar los nexos existentes entre la habilidad usar asistentes matemáticos, en su condición de invariante y los contenidos específicos de la disciplina MS lo que favorece la integración de los AM al currículo de dicha disciplina para las carreras de ingeniería.