Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Uno de los momentos más transcendentales del desarrollo de la enseñanza superior lo constituyó la creación de centros de educación superior militares, a partir del Decreto Ley No. 90/09 de 15 de diciembre de 2005, cuyo objetivo es formar los efectivos de las Fuerzas Armadas Angolanas.
El proceso de enseñanza-aprendizaje (PEA) de la Geometría Analítica en la Academia de la Fuerza Aérea Nacional (AFAN) de Angola tiene una alta incidencia en la formación de pilotos aviadores. La solución de problemas profesionales del futuro egresado, requieren del dominio de conceptos y de la solución de problemas geométricos, aunque se vinculan también a conocimientos de otras materias vinculadas a la Física, la Ingeniería y la Aeronáutica.
En la producción científica y metodológica se evidencia la importancia del aprendizaje de la Geometría desde edades tempranas. Sobre este particular (Barrantes y Barrantes, 2020) expresan:
La principal finalidad de la enseñanza-aprendizaje de la geometría es conectar a los alumnos con el mundo en el que se mueven pues el conocimiento, la intuición y las relaciones geométricas resultan muy útiles en la vida cotidiana, para ubicarse en el espacio, reconocimiento de formas, diseño, arte o estudios relacionados con las ciencias. (p.13)
El aprendizaje de conocimientos de geometría analítica constituye una parte esencial de los conocimientos matemáticos requeridos, sin la cual no es posible cumplir plenamente con los objetivos determinados por la AFAN en la formación de pilotos aviadores.
Un ejemplo concreto lo constituye el estudio de las curvas a partir de su relación con la realidad cotidiana, a partir de que todo objeto en movimiento describe una curva en el espacio. Nociones intuitivas como el vuelo de aves y mariposas, la trayectoria de vehículos automotores, la trayectoria de un avión durante el ascenso, vuelo o descenso, entre otras situaciones similares, permiten introducir el tema mencionado.
En el estudio exploratorio realizado para esta investigación, se pudo constatar que el PEA de la Geometría Analítica en la AFAN no está exento de dificultades y aún lejos de alcanzar la finalidad declarada. Al revisar los planes, programas, soporte bibliográfico (AFAN, 2018), así como las actas de colectivo y la experiencia práctica en la enseñanza de esta disciplina, se evidencia que persisten una serie de dificultades con relación a su tratamiento, algunas de las cuales están vinculadas al poco dominio del profesor acerca de los componentes didácticos del PEA y, en particular, al uso limitado o casi nulo de las tecnologías de la información y las comunicaciones en el citado proceso.
El PEA, caracterizado ampliamente en la extensa bibliografía científica y metodológica consultada (Clavijo, 2020; Osorio, 2021; Ramírez, 2022; Torres y otros, 2022; entre otros), constituye la integración de lo instructivo con lo educativo y tiene como propósito esencial contribuir a la formación integral de la personalidad del estudiante.
En el PEA de la Matemática existen innumerables trabajos con concepciones desarrolladoras explícitas. Se consultaron, entre otros, los trabajos de Ortiz, García y Enrique (2018); Coro (2019); Naveira (2022); Barcos, López y Sánchez (2023).
Particular atención se hace acerca de los componentes didácticos del PEA. Se asume la conceptuación de la Dra. Cs. Fátima Addine (2004), al expresar la relación entre los componentes determinados: objetivo, contenido, métodos de enseñanza - aprendizaje, medios de enseñanza - aprendizaje, evaluación y las formas de organización del proceso, así como las que se establecen con los protagonistas esenciales del proceso (denominados también actores del PEA), el profesor, los estudiantes y el grupo.
El uso de GeoGebra para el desarrollo del PEA de la Geometría Analítica en la AFAN ha constituido un punto de partida en la intencionalidad de proporcionar mayor dinamismo a este proceso que, a su vez, propicia un aprendizaje significativo de conocimientos geométricos importantes para resolver problemas del futuro piloto aviador, así como responde también a las otras dos dimensiones del aprendizaje desarrollador: la motivación y la autorregulación (Castellanos y otros, 2002).
Las dificultades obtenidas en el estudio exploratorio muestran las carencias didácticas básicas del profesor de Matemática que se desempeña en la AFAN, las que unidas a los referentes teóricos y metodológicos expuestos, determinan que el tema de investigación es el proceso de enseñanza-aprendizaje de la Geometría Analítica en esta institución militar de nivel superior y el problema ¿Cómo contribuir al proceso de enseñanza-aprendizaje de la Geometría Analítica desde la preparación didáctica básica del profesor de Matemática de la AFAN?
En tal sentido, el presente artículo tiene como objetivo determinar las acciones de preparación del profesor para la dirección del PEA de la Geometría Analítica, desde la mediación del asistente GeoGebra para la solución de problemas geométricos.
Materiales y métodos
Esta investigación está enmarcada en un enfoque mixto, por cuanto se integra lo cuantitativo y lo cualitativo en el estudio sobre el uso de GeoGebra en la resolución de problemas geométricos para el desarrollo del PEA de la Geometría Analítica, lo que permitió recuperar la información suficiente y necesaria para la realización de la investigación en diversas obras visibles en bases de datos indexadas y otras publicaciones, lo que también hizo posible el seguimiento del estado del arte del tema.
Para la investigación se emplearon los métodos de investigación teóricos siguientes:
Análisis - Síntesis: El análisis permitió estudiar los diferentes factores que influyen en el proceso de enseñanza-aprendizaje de la Matemática y, en particular, de la Geometría Analítica. Mediante la síntesis se establecieron las relaciones entre los factores estudiados y los problemas de la profesión que pueden ser resueltos por los estudiantes en este nivel de formación.
Inducción - Deducción: En la investigación se parte del presupuesto de la importancia que tiene para la preparación geométrica de los estudiantes, el establecimiento de la relación entre el conocimiento y la práctica, para poder determinar soluciones a los problemas particulares mediante el uso de los conocimientos de la Matemática y en particular los concernientes a la Geometría Analítica. De las soluciones a estos problemas particulares se determinan regularidades que posibilitan generalizar orientaciones metodológicas para el tratamiento de este contenido.
Modelación: Para concebir y determinar las acciones que potencian la preparación del profesor en la dirección del PEA de la Geometría Analítica para la formación del piloto aviador.
Igualmente fueron aplicados métodos del nivel empírico:
Análisis documental: Para el estudio de los antecedentes en la formación del piloto aviador, en correspondencia con los documentos normativos vigentes y resultados académicos y científicos en torno al tema de la investigación.
Encuestas: Para obtener información sobre las características del PEA de la Geometría Analítica y para la autoevaluación por parte de los profesores del desarrollo de sus habilidades para dirigir el PEA de la Geometría Analítica.
Encuesta de satisfacción: aplicada a los beneficiarios directos, profesores de Geometría Analítica, para conocer sus criterios tras la implementación de las acciones propuestas.
Como métodos estadísticos, la distribución de frecuencias absolutas y relativas porcentual.
En el proceso de investigación fueron involucrados los siete (7) profesores de Matemática que imparten docencia en la AFAN, con mayor intencionalidad en los dos (2) profesores que desarrollaron la Geometría Analítica en los cursos lectivos de 2019 a 2021.
A los siete profesores se les aplicó una encuesta para conocer el dominio de conocimientos geométricos y didácticos que poseían antes de la determinación de las acciones de preparación propuestas, para después aplicar la encuesta de satisfacción en cuanto a la preparación recibida y los resultados cualitativos que se derivaron de la preparación.
La investigación tiene una alta significación en el contexto angoleño, máxime en el entorno universitario militar, donde se aportaron soluciones prácticas a la situación real de desconocimiento básico acerca de los componentes didácticos del PEA que tiene el profesor de Matemática, sumergido en una sociedad cada vez más tecnológica y, al mismo tiempo, desconocedor de la relevancia del uso de las TICs en el PEA de la Geometría Analítica.
En esencia, en la investigación se desarrollaron las tareas de investigación siguientes:
Estudio exploratorio para la determinación de las carencias del profesor en la dirección del PEA.
Sistematización teórica-metodológica del PEA de la Geometría Analítica, desde los componentes didácticos del proceso y en particular, en el uso de las TICs como mediadores en este proceso.
Propuesta de acciones para la preparación básica del profesor de Matemática.
Estado de satisfacción de los profesores acerca de la propuesta.
Resultados
Con la aplicación del método de análisis documental, se analizaron los contenidos descritos en el programa de formación de Piloto Aviador, a través de la revisión de los siguientes documentos:
Plan de Estudio
Programas de la asignatura
Actas de los Consejos de curso
Actas de reuniones del colectivo de profesores de asignatura
Estos documentos se analizaron a partir de una guía confeccionada a tales efectos y muestran lo siguiente:
Correspondencia entre el perfil del egresado de esta especialidad de piloto Aviador, con los objetivos de la carrera, la asignatura y la disciplina (GA), donde los contenidos declarados son necesarios, aunque no suficientes, para lograr una adecuada formación.
Los programas de la Carrera de Licenciatura de Piloto Aviador de la AFAN y las orientaciones metodológicas correspondientes, no responden a todas las expectativas de las exigencias actuales de la reforma educativa.
Declaran en los objetivos del programa la necesidad de la comprensión de los conocimientos de geometría analítica, pero no existen recomendaciones de cómo lograrlo, para que, a partir de la fundamentación matemática, los estudiantes de esta carrera puedan razonar correctamente y aprendan métodos de demostración, que les permitan desarrollar sus capacidades en la resolución de problemas para analizar fenómenos técnicos y científicos, vinculados a su futura profesión.
Declaran como objetivo prioritario el uso de medios informáticos para el mejoramiento del proceso de enseñanza-aprendizaje.
Los materiales que disponen los profesores para su guía y preparación (programas para las clases, libros de texto, y otros), se caracterizan por contar con información muy general, y en ocasiones nula, sobre el modo de usar las TICs como mediadores del PEA.
El insuficiente desarrollo de la aprehensión de los conocimientos geométricos en los futuros profesionales de la aviación, lo que conduce a la idea del bajo nivel de aprendizaje de estos conocimientos que reciben de sus profesores o por otras vías y ello afecta la posibilidad de resolver problemas profesionales donde se aplican conocimientos geométricos.
Necesidad de profesores con calificación profesional y dominio de todas las herramientas geométricas y didácticas para aclarar debidamente a los estudiantes, lo cual resulta también deficiente.
Los profesores no consultan suficiente bibliografía y no poseen las habilidades para buscar en la bibliografía existente impresa o digital, lo cual no favorece la revisión de los procedimientos de resolución de problemas geométricos de forma analítica, debidamente explicados que pueden encontrarse.
Los profesores desarrollan clases tradicionales, donde predomina el método expositivo y la resolución de ejercicios típicos. No poseen conocimientos didácticos para involucrar a todos los actores del PEA de manera integrada.
No se evidencia el uso sistemático de recursos informáticos para el desarrollo del PEA de la Geometría Analítica.
Además de este análisis documental, fueron aplicados otros dos instrumentos para constatar los resultados preliminares obtenidos: encuesta a profesores y observación a clases.
La encuesta a los siete profesores buscaba información acerca del dominio de los conocimientos geométricos por parte de los estudiantes (Tabla 1), las habilidades para la resolución de problemas (Tabla 2) y su labor en la dirección del PEA de la Geometría Analítica (Tabla 3).
Tabla 1 - Dominio de conocimientos geométricos por parte de los estudiantes
| Conocimiento | Reconocen dominio | No reconocen dominio |
|---|---|---|
| Transformación de la ecuación a la forma canónica | 5 | 0 |
| Aplicación de conceptos y propiedades de las curvas y superficies estudiadas a la identificación del gráfico correspondiente a la ecuación | 1 | 6 |
| Determinación de los interceptos con los ejes coordenados | 5 | 2 |
| Determinación de las trazas en los planos coordenados | 3 | 4 |
| Análisis de la simetría | 1 | 6 |
| Análisis de la extensión | 0 | 7 |
| Determinación de secciones planas paralelas a los planos coordenados | 0 | 7 |
| Trazado del gráfico | 1 | 6 |
| Identificación de la curva o superficie correspondiente al gráfico | 5 | |
| Aplicación de conceptos y propiedades de curvas y superficies estudiadas a la determinación de la forma general de la ecuación, en correspondencia con la posición de la curva (superficie) en el plano (espacio) | 0 | 7 |
| Determinación de los valores de los coeficientes de los términos de la ecuación | 0 | 7 |
| Precisión de la ecuación de la curva o superficie correspondiente al gráfico | 0 | 7 |
| Uso de las TIC para el trazado del gráfico o su identificación y para la representación y la determinación de sus elementos. | 0 | 7 |
Tabla 2 - Dominio de acciones en la resolución de problemas
| Acciones | Reconocen dominio | No reconocen dominio |
|---|---|---|
| Lectura y familiarización con el problema | 3 | 4 |
| Análisis de la información que se ofrece para determinar la incógnita | 1 | 6 |
| Determinación de la relación entre los datos y la incógnita | 2 | 5 |
| Modelación de la situación planteada en el problema | 0 | 7 |
| Elaboración de un plan de solución | 0 | 7 |
| Ejecución del plan de solución | 0 | 7 |
| Examen del resultado obtenido | 0 | 7 |
| Examen del razonamiento empleado en la obtención del resultado | 0 | 7 |
| Análisis de otras vías de obtener el resultado | 0 | 7 |
| Análisis de la posible aplicación del resultado en la solución de otros problemas | 0 | 7 |
| Análisis de la posible aplicación del método empleado en la solución de otros problemas | 0 | 7 |
Tabla 3 - Autovaloración acerca de la gestión de dirección del PEA
| Acciones | Sí | No |
|---|---|---|
| Establecimiento de las relaciones entre los procedimientos para la solución de ejercicios y los contenidos estudiados | 4 | 3 |
| Explicación de los conceptos, juicios de valores, convicciones, razonamientos lógicos y procedimientos, relacionados con la solución del ejercicio o problema de forma ordenada | 5 | 2 |
| Identificación de los componentes didácticos del PEA y sus relaciones | 1 | 5 |
| Selección y utilización de los medios de enseñanza-aprendizaje apropiados, incluyendo los recursos informáticos, para la comunicación de los resultados | 3 | 4 |
| Identificación de las carencias y potencialidades de cada estudiante con respecto a los conocimientos que se requieren | 2 | 5 |
| Promoción de la motivación hacia el aprendizaje de los conocimientos geométricos y su aplicación a la profesión | 3 | 4 |
| Gestión de actitudes, valores y métodos y formas de trabajo | 4 | 3 |
| Promoción del trabajo colaborativo en grupo para potenciar el aprendizaje | 2 | 5 |
La observación a clases (Tabla 4) se realizó a los dos profesores que impartieron la Geometría Analítica (dos a cada uno) para constatar los aspectos de la guía elaborada a tales efectos. Para ello, el investigador se acompañaba de otro profesor de Matemática de la AFAN y al término de cada clase visitada se realizó la valoración de cada aspecto de la guía de manera conjunta.
Para la observación se determinaron los códigos siguientes:
No se aprecian resultados en correspondencia con el aspecto valorado o son, en sentido general, de muy mala calidad
Se aprecian pocos resultados en correspondencia con el aspecto valorado o son, en sentido general, de baja calidad
Se aprecian varios resultados en correspondencia con el aspecto valorado y en general tienen una calidad adecuada
Se aprecian varios resultados en correspondencia con el aspecto valorado y todos tienen calidad adecuada, con pocos señalamientos relevantes
Las acciones concebidas son suficientes, tienen adecuada calidad y no hay señalamientos, además de demostrar creatividad en su realización
Tabla 4 - Resultados de la revisión de clases
| Aspectos | C1 | C2 | C3 | C4 | PROM | |
|---|---|---|---|---|---|---|
| Acerca del CONTENIDO determinado para la clase | 3 | 3 | 2 | 3 | 3 | |
| 1 | Correspondencia con el objetivo determinado para la clase | 3 | 4 | 3 | 4 | 4 |
| 2 | Dominio del contenido por parte del profesor | 3 | 4 | 3 | 4 | 4 |
| 3 | Acciones que evidencian el aprovechamiento de las potencialidades educativas del contenido en la formación | 2 | 2 | 1 | 1 | 2 |
| Acerca de la estructuración metodológica de la clase | 2 | 2 | 2 | 2 | 2 | |
| 4 | Declaración clara y precisa del objetivo planteado para la clase | 4 | 4 | 4 | 3 | 4 |
| 5 | Orientación para el logro del objetivo planteado (OHO) para la clase | 1 | 1 | 2 | 1 | 1 |
| 6 | Aseguramiento del nivel de partida (ANP) para el desarrollo de la clase | 3 | 4 | 3 | 4 | 4 |
| 7 | Motivación (MOT) en los estudiantes para el contenido de la clase y demostración de la necesidad de conocimientos | 2 | 1 | 3 | 2 | 2 |
| 8 | Planteamiento de un problema inicial para la obtención o fijación de conocimientos o procedimientos | 1 | 1 | 1 | 1 | 1 |
| 9 | Acciones para la participación de los estudiantes en la obtención y/o fijación de conocimientos y procedimientos | 1 | 1 | 3 | 4 | 2 |
| 10 | Organización para el trabajo grupal en la obtención y/o fijación de conocimientos. | 1 | 1 | 1 | 2 | 1 |
| 11 | Empleo de medios de enseñanza aprendizaje durante el desarrollo de la clase | 1 | 2 | 2 | 1 | 2 |
| 12 | Acciones para resumir los principales resultados en el cumplimiento del objetivo | 2 | 3 | 2 | 2 | 2 |
| Consideraciones retrospectivas y perspectivas | 3 | 3 | 4 | 3 | 3 | |
| 13 | Participación activa e independiente de los estudiantes acerca de la valoración de su aprendizaje sobre el contenido de la clase | 1 | 1 | 2 | 1 | 1 |
| 14 | Aprendizaje logrado en el grupo de estudiantes evidenciado en las acciones de fijación | 2 | 2 | 3 | 2 | 2 |
| 15 | Apariencia personal del profesor, de los estudiantes y condiciones e higiene del salón de clases | 4 | 4 | 5 | 4 | 4 |
| 16 | Relaciones profesor - estudiantes - grupo | 2 | 2 | 4 | 4 | 3 |
| 17 | Disciplina formal y profesional de los estudiantes | 4 | 4 | 4 | 4 | 4 |
| 18 | Percepción sobre la autovaloración del profesor acerca de los resultados de la clase | 3 | 2 | 4 | 2 | 3 |
Leyenda: C-Clase PROM: Promedio de valoración del aspecto
La sistematización realizada acerca del PEA y de sus componentes didácticos, posibilitó determinar un resumen de aspectos esenciales en la preparación de los profesores para gestionar la dirección de este proceso en la AFAN.
Se asumieron las caracterizaciones y relaciones como resultado del estudio de los componentes didácticos enunciados por Addine (2004) y otros resultados de varios autores.
Objetivo: Es el componente rector del PEA. Determina el propósito que se requiere formar en los estudiantes. Orienta la configuración adoptada por el resto de los componentes. Responde a las preguntas ¿para qué enseñar? ¿para qué aprender?
Contenido: Vinculado directamente al objetivo determinado, expresa la respuesta a las preguntas ¿qué enseñar? ¿qué aprender? Se asume como contenido toda la cultura y experiencia social a adquirir por los futuros profesionales, en correspondencia con los objetivos.
Para el mejoramiento didáctico del profesor de Matemática que forma al Piloto Aviador y en particular de Geometría Analítica, resulta necesario que este tenga dominio de qué se entiende por contenidos. En la presente investigación se asumió que, para el PEA de la Geometría Analítica, es necesario que se consideren como contenidos, desde los fundamentos anteriormente asumidos y tomando como base lo expresado por Quintana (2011, p.29), con adecuaciones contextualizadas de los autores del presente trabajo:
Los conceptos (expresados en forma de caracterizaciones o definiciones) y proposiciones matemáticas (teoremas).
Los métodos y procedimientos (heurísticos y algorítmicos) acompañados de sus técnicas de trabajo mental y práctico.
Las ideas filosóficas, sociales, científicas y valores.
Las habilidades y formas flexibles de pensamiento que el estudiante sea capaz de utilizar por sí mismo autorreguladamente.
Las estrategias, no sólo cognitivas sino metacognitivas y en particular las referidas a la resolución de problemas geométricos, vinculados a la profesión de Piloto Aviador.
Método de enseñanza - aprendizaje: Contribuye al desarrollo de los contenidos, en correspondencia a los objetivos determinados, dando respuesta a las preguntas ¿cómo enseñar? ¿cómo aprender? ¿cómo desarrollar los contenidos? Este es el componente dinámico del PEA. El método orienta las acciones y operaciones del profesor para que los estudiantes se apropien del contenido y logren los objetivos propuestos.
Medio de enseñanza - aprendizaje: Los medios de enseñanza son todos aquellos elementos que sirven de soporte material a los métodos de enseñanza - aprendizaje para posibilitar el logro de los objetivos. Los medios de enseñanza y aprendizaje responden a la interrogante ¿Con qué enseñar y aprender?
Sobre este particular, se profundiza más adelante, a partir de la idea de utilización de GeoGebra como mediador del PEA.
Formas de organización: Constituye el componente integrador del PEA, donde se expresan las relaciones entre los protagonistas principales del proceso, el profesor, los estudiantes, el grupo, en la dimensión temporal y espacial del mismo. Este debe reflejar no sólo los espacios y tiempos tradicionales de desarrollo del PEA, sino también los que resultan de la interacción orientada con las redes sociales y del aprendizaje autorregulado con el uso de las TIC.
Evaluación: Expresa el carácter regulador en el PEA. Sus funciones generales son: diagnóstica, instructiva, educativa, desarrolladora y de control. Juega un rol trascendental en el cambio educativo, aunque resulta ser el componente que evidencia en su concepción menos desarrollo.
Para la presente investigación y como parte de la preparación del profesor de Matemática, los autores apuntan aspectos esenciales a considerar en la evaluación:
Diagnosticar de manera dinámica, continua e integral al estudiante en formación.
Evaluar el aprendizaje multidimensionalmente, abarcando, en síntesis, el aprender a conocer, hacer, ser y convivir.
Establecer la calidad de los nuevos aprendizajes, es decir, su solidez y duración y sus posibilidades de ser aplicado o transferido a situaciones nuevas, o sea, su funcionalidad.
Evaluar y valorar la calidad del PEA, con la participación activa de todos los actores del PEA.
Junto a los componentes didácticos del PEA, los profesores requieren tener otros elementos básicos de Didáctica, fundamentales para desarrollar este proceso con mayor calidad. Entre estos elementos básicos, resulta importante dotarlos de reseñas acerca de los rasgos esenciales que tipifican todo PEA: carácter sistémico, carácter procesal, carácter multilateral, carácter dialéctico, carácter contextual y carácter legal.
Estudios más recientes utilizan las premisas generales descritas, pero revelan nuevos elementos de suma importancia que tienen lugar en la educación superior. Naveira y González (2021) expresan que en dependencia del contexto donde se desarrolla el sujeto y tomando como base el carácter de las relaciones con ese contexto, se configuran los recursos subjetivos, por lo que se deben considerar aspectos comunes a los estudiantes en esta etapa.
Para el desarrollo del PEA de la Matemática en la República de Angola, resulta muy interesante la aplicación de la Teoría de la Subjetividad desde una perspectiva histórico - cultural, por lo que se consideran elementos tales como:
Elaboración y puesta en marcha del proyecto de vida: incluye las relaciones de todas las actividades sociales de la persona (trabajo, profesión, familia, tiempo libre, actividad cultural, socio-política, relaciones interpersonales de amistad y amorosas, organizacionales, etc.), comunes e influyentes en el contexto universitario de Angola.
Subjetividad social, la cual permite la comprensión de los procesos subjetivos que tienen lugar en un grupo social dado. Está dada por las características propias del lugar donde se desarrolla socialmente el individuo, sin que represente la suma de las subjetividades individuales. Este elemento permite también la comprensión del Grupo como componente del PEA.
El dominio por los profesores de la integración de los componentes didácticos, tiene una incidencia fundamental en los estudiantes en formación como Piloto Aviador. En particular, lo referido al aprendizaje individual y grupal de los mismos, con costumbres y hábitos diferentes, lo que constituye un problema social.
Se retoma ahora el componente medio de enseñanza-aprendizaje, para resaltar los resultados esenciales desde la fundamentación del uso de las TIC y desde la utilización práctica del asistente GeoGebra como mediador del PEA de la Geometría Analítica en la AFAN.
No existen dudas que las TIC constituyen potentes herramientas de trabajo en la Educación, pues entre otras alternativas, posibilitan la creación de medios de enseñanza-aprendizaje, que revolucionan a su vez los métodos, las formas organizativas y, de manera general, la forma de concebir todos los demás componentes didácticos de este proceso.
Implica cambiar la actitud hacia la Matemática, las formas de visualización, experimentación y simulación de relaciones y procesos, que significan cambiar la forma, la concepción de hacer y enseñar esta ciencia, significa modificar las formas de pensar y de actuar.
En el caso de disciplinas como el Análisis, el Álgebra y la Geometría (y por ende en la Geometría Analítica) han surgido numerosos software y páginas web para el proceso de enseñanza de estas disciplinas matemáticas. Muchas de las aplicaciones son de acceso gratuito, entre las que se pueden citar GEOMETRYX, GEOMETRÍA DE BOLSILLO, NaNGEOMETRÍA, FÓRMULAS GEOMÉTRICAS, GEOMETRY MATHEMATICS, xGEOMETRY, ISOSCELES y GEOGEBRA.
El uso de estos medios se distingue de las formas tradicionales por su exactitud, limpieza, precisión y, esencialmente, por el dinamismo que pueden adquirir las figuras geométricas y los cuerpos, además de las posibilidades de interacción con los sujetos (estudiantes, grupo y profesores), quienes pueden manipular las representaciones y explorarlas en pocos segundos, evaluarlas, predecir generalizaciones y plantearse hipótesis que deben ser validadas con la demostración geométrica.
Con esta posibilidad de acceso a la manipulación directa, la enseñanza de la Geometría Analítica ofrece una interesante alternativa hacia una nueva conceptualización, como resulta el estudio de las propiedades invariantes de las figuras geométricas. Al permitir la posibilidad de experimentar con una especie de “materialización” de los objetos matemáticos, de sus representaciones y de sus relaciones, los estudiantes pueden vivir un tipo de experimentación matemática que otras formas de aprendizaje no proporcionan (Castiblanco, 2004, p. 20).
La intencionalidad del uso de GeoGebra, debe acompañarse con la integración coherente al sistema de medios de enseñanza-aprendizaje que se conciba. Inclusive, se deberá tener en cuenta en lo adelante, la incorporación de recursos vinculados con la inteligencia artificial, los cuales se abren paso vertiginosamente y sus aplicaciones en el PEA no se harán esperar.
La selección de este recurso informático está dada por diversos elementos, que tienen su origen en el incremento significativo del uso de esta herramienta por universidades, centros educacionales y otras instituciones científicas y productivas.
En la página web oficial de GeoGebra (2023) se pueden detallar las principales características de este software, acá resumidas:
Es una plataforma en línea con más de un millón de recursos gratuitos.
Todos los recursos se pueden compartir de manera fácil en la sección CLASSROOM de la plataforma.
Se puede monitorear el progreso de los estudiantes en tiempo real.
Se ha convertido en el proveedor líder de software de matemáticas dinámicas.
Desde 2021, forma parte de la familia BYJU, empresa de tecnología educativa india más valiosa del mundo.
Baena (2020) presenta diferentes recursos de Geogebra para el PEA de la Geometría Analítica. Destaca particularmente, algunos contenidos para los cuales existen recursos en las redes de fácil acceso:
Posiciones relativas de recta y plano, de dos planos, de tres planos y de dos rectas
Haz de planos secantes y paralelos
Ángulo entre dos rectas, entre una recta y un plano, entre dos planos
Distancia de un punto a un plano, entre dos planos, entre una recta y un plano, de un punto a una recta, entre rectas cruzadas
Proyección ortogonal y simétrica
Problemas recurrentes: perpendicular común a dos rectas que se cruzan, intersección de una recta con un plano perpendicular, recta paralela a dos planos que pasa por un punto, recta perpendicular a otra recta contenida en un plano, plano perpendicular a otro que contiene una recta
Todo lo anterior permitió considerar el uso de GeoGebra en la resolución de determinados problemas geométricos que tienen incidencia en la resolución de problemas profesionales del piloto aviador, como parte de las acciones de preparación del profesor para el PEA de la Geometría Analítica en la AFAN.
Lo más interesante en esta preparación resultó, especialmente para los beneficiarios, la presentación de ejemplos concretos del uso de GeoGebra en la resolución de problemas geométricos, paso a paso. Se muestran algunos de estos ejemplos, con sus resultados utilizando el asistente:
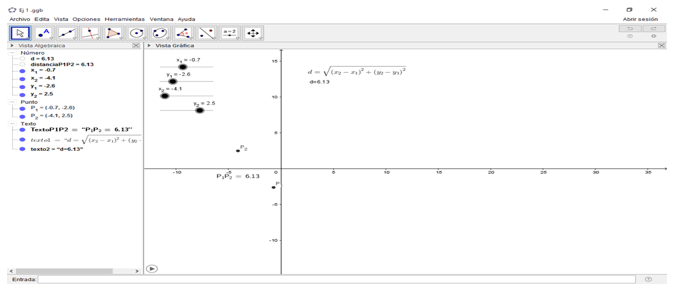
Ejemplo 1: Comprueba, utilizando las herramientas de GeoGebra, que la distancia entre dos puntos del plano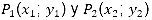 
puede calcularse mediante la fórmula: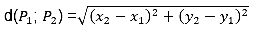 
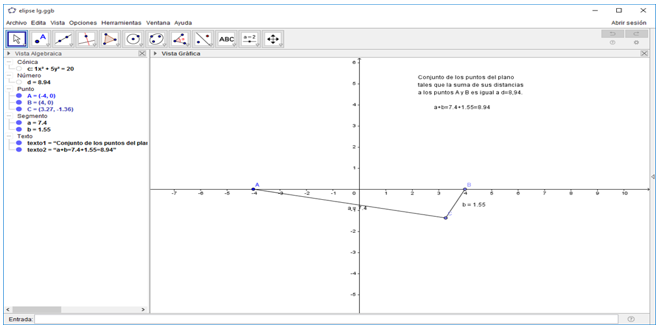
Ejemplo 2: En el applet “Ejemplo 2”, activa el rastro del punto P e identifica el lugar geométrico que se obtiene al mover este punto y determina cuál es la condición que satisfacen esos puntos.
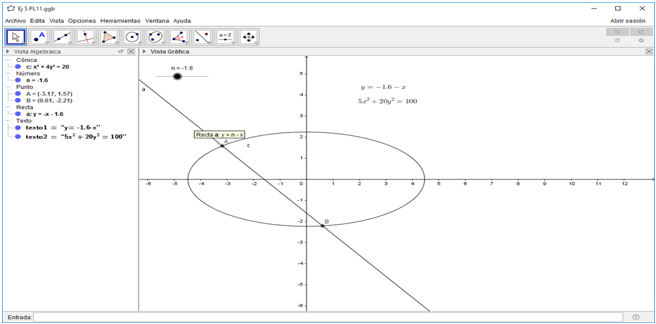
Ejemplo 3: ¿Para qué valores de nÎÂ la recta y = n -x es tangente, secante o exterior a la elipse ?
Igualmente fueron desarrollados con los profesores otros ejemplos, donde la solución del problema geométrico, tiene incidencia en la solución de un problema profesional. En una publicación anterior de los autores se presentan dos ejemplos resueltos, los cuales evidencian la intencionalidad en propiciar la motivación y la significatividad que debe imperar en las clases de Geometría Analítica en la AFAN.
De esta manera, se elaboraron las acciones que conformaron la preparación básica de los profesores de Matemática en la AFAN, tal y como se ilustran en la tabla 5.
Tabla 5 - Aspectos esenciales incluidos en la preparación didáctica básica del profesor de Matemática de la AFAN
| Tema | Acciones | Observaciones |
|---|---|---|
| Planes y programas | Análisis del programa académico de Geometría Analítica (GA) y sus orientaciones metodológicas | Se realiza en el colectivo de disciplina con la dirección del investigador principal, con el objetivo de precisar cómo se implementan las orientaciones metodológicas previstas y cuáles deben implementarse, aun sin estar previstas. |
| Desarrollo de los conocimientos geométricos a dominar en las clases de GA | El trabajo colectivo debe garantizar el dominio por parte de los profesores de los conocimientos geométricos que se tratan en la disciplina GA en la AFAN, así como establecer relaciones interdisciplinarias de los mismos. | |
| Determinación de conocimientos geométricos que contribuyen a resolver problemas profesionales | Siguiendo el procedimiento determinado por el investigador, para la determinación de las invariantes de conocimientos geométricos necesarios en la resolución de problemas profesionales y que forman parte del programa académico, realizar la determinación colectiva de estos conocimientos. | |
| Componentes didácticos | Análisis de los componentes didácticos del PEA y sus relaciones | Presentar al colectivo de profesores de Matemática, los elementos esenciales de los componentes didácticos de este proceso, para profundizar en las relaciones entre todos los componentes y su aplicabilidad en el PEA de la GA. |
| Criterios de selección y/o elaboración de medios de enseñanza - aprendizaje e identificación de sus potencialidades en el PEA | Enfatizar en el componente MEDIO DE ENSEÑANZA-APRENDIZAJE y su rol como mediador de este proceso con el uso de asistentes geométricos como GeoGebra en la resolución de problemas geométricos, de manera integrada en el sistema de medios concebidos para la asignatura. | |
| Determinación de las formas organizativas para el PEA de la GA en correspondencia con los restantes componentes del PEA | A partir del diagnóstico de los estudiantes en formación y de los resultados determinados en las acciones precedentes, precisar las formas de organización para las clases de GA, que incluyen actividades docentes fuera del entorno habitual del salón de clases. | |
| Consideraciones acerca de la evaluación | Se analizan colectivamente los aspectos esenciales a considerar en la evaluación, con la necesidad de la participación de todos los protagonistas del PEA en el proceso evaluativo. | |
| Estructuración metodológica de la clase de GA | En estrecha relación con los componentes didácticos del PEA, explicar las funciones didácticas desde el PEA de la GA, de manera que se estructuren metodológicamente las clases de GA con mayor calidad y en correspondencia con los elementos básicos de Didáctica tratados. | |
| PEA desarrollador | Sistematización de concepciones de enseñanza y aprendizaje desarrolladores | Con el trabajo colectivo de los profesores de Matemática, bajo la conducción del investigador principal, se revisan las concepciones de enseñanza y aprendizaje desarrolladores de avanzada. Se contextualizan a la sociedad angoleña y al entorno universitario en la academia militar. |
| Orientaciones para el tratamiento de las tres dimensiones del aprendizaje desarrollador | Se analizan en colectivo las tres dimensiones del aprendizaje desarrollador: activación-regulación, significatividad y motivación. Se profundiza en subdimensiones como la metacognitiva, el establecimiento de relaciones significativas y el sistema de autovaloraciones y expectativas positivas hacia el aprendizaje. | |
| Trabajo colaborativo | Concepciones e ideas acerca del trabajo colaborativo | Es importante preparar a los profesores en técnicas de trabajo grupales que propicien el trabajo colaborativo y potencien el aprendizaje, trabajando a partir del diagnóstico de los estudiantes en formación y sobre el estado actual y potencial de cada uno de ellos. |
La preparación realizada a los siete profesores de Matemática de la AFAN tuvo una amplia aceptación entre los profesores, los estudiantes y los directivos de la academia, por la implicación que tuvo en el desarrollo del PEA de la Geometría Analítica y en las actividades prácticas de vuelo de los estudiantes en formación.
Se muestran a continuación (tabla 6) los resultados de la aplicación de la encuesta de satisfacción a los profesores involucrados en la preparación. Se utiliza la escala de 1 a 5, donde 1 representa el valor de menor reconocimiento y 5 la de mayor reconocimiento:
Tabla 6 - Resultados de la encuesta de satisfacción
| Aspecto valorado | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Sobre la preparación recibida: | |||||
| Contribución de la preparación a la labor como profesor | 2 | 1 | 4 | ||
| Conocimientos adquiridos sobre los componentes del PEA y sus relaciones | 3 | 4 | |||
| Conocimientos adquiridos sobre uso del asistente GeoGebra en el PEA | 3 | 4 | |||
| Relevancia de los problemas geométricos resueltos con el uso del asistente | 5 | 2 | |||
| Sobre el impacto de la preparación: | |||||
| Calidad de las clases preparadas y desarrolladas tras la preparación | 1 | 4 | 2 | ||
| Reconocimiento de la calidad de las clases por los estudiantes en formación | 1 | 5 | 1 | ||
| Nivel de participación en el aprendizaje de los diferentes actores del PEA | 2 | 5 | |||
| Resultados del trabajo colaborativo en el aprendizaje | 3 | 4 | |||
| Motivación y significatividad de los contenidos desarrollados | 2 | 3 | 2 | ||
Discusión
Los elementos básicos de Didáctica, particularmente los componentes del PEA y las relaciones entre estos componentes, relacionados en el presente artículo, constituyen una novedad en países con avances aún discretos en materia de enseñanza y aprendizaje, como es el caso de la educación universitaria en Angola.
En los últimos años, gracias a los intercambios con profesionales de Brasil, Portugal, Cuba y otras naciones europeas en menor escala, se da un impulso notable a este tema en el marco de transformaciones en los lineamientos y en la aplicación de las líneas maestras de la educación superior en el país.
Son numerosos y diversos los aportes al PEA de la Matemática y sus ramas que han realizado estudiosos del tema, a partir de las concepciones generales de Didáctica y, en particular, a la atención de los componentes didácticos y sus relaciones en este proceso. Sobre la base de lo general (Addine, 2004) en cuanto a la Didáctica y sobre la concepción desarrolladora del PEA (Castellanos y otros, 2002), se han elaborado propuestas de estrategias, concepciones y proyectos que enriquecen la enseñanza de la Matemática y, en particular, del análisis, la geometría y el álgebra (Coro (2019); Naveira (2022); Barcos, López y Sánchez (2023).
La sistematización acerca de estos componentes, permite profundizar en cada uno de ellos, especialmente en el componente medio de enseñanza-aprendizaje desde la concepción del uso de las tecnologías de la información y las comunicaciones (TIC) como mediadores en el PEA de la Geometría Analítica.
En los trabajos de los investigadores reseñados (Ortiz, García y Enrique, 2018); Coro, 2019); Naveira, 2022; Barcos, López y Sánchez, 2023), se recogen propuestas encaminadas a potenciar el aprendizaje desarrollador de la Matemática, esencialmente en los niveles medio y superior.
Muchos asumen el desarrollo de estrategias, no sólo cognitivas, sino metacognitivas y en particular las referidas a la resolución de problemas, convirtiéndolas de hecho en contenido de enseñanza, lo que constituye un referente para esta investigación.
Las concepciones de avanzada del PEA resaltan el carácter desarrollador que debe tener este proceso, si es que se pretende formar a un profesional integral que no sólo exhiba conocimientos, sino que desarrolle habilidades profesionales, capacidades, valores y modos de actuación acordes a la sociedad donde se desarrolla el individuo.
Las regularidades determinadas en este estudio posibilitan diseñar una concepción desarrolladora del PEA de la Geometría Analítica en la AFAN, con la inclusión de elementos determinados por los autores en cuanto a la vinculación de los problemas geométricos a los problemas profesionales de los pilotos aviadores, lo cual constituye un elemento esencial en la preparación de profesores para la estructuración metodológica de las clases correspondientes.
De igual manera se sistematizan concepciones teórico-prácticas del uso del asistente GeoGebra como mediador del PEA de la Matemática, en particular de la Geometría Analítica, desde la consulta a diversas fuentes que abordan este proceso en diferentes escenarios (Hernández y otros, 2022; Domingo-Coscollola y otros, 2020; López y otros, 2021), entre otros trabajos que se desarrollan desde el proyecto 'El GeoGebra en el Proceso de enseñanza-aprendizaje de la Matemática'.
Estos resultados contribuyen de manera determinante a la utilización de este asistente, en función de resolver problemas geométricos, vinculados a problemas profesionales del Piloto Aviador. El aporte práctico de los autores de este artículo radica precisamente en la vinculación a los problemas de la profesión de los futuros egresados como pilotos aviadores, lo que garantiza la significatividad del aprendizaje en los estudiantes en formación.
Finalmente, los resultados determinados en este trabajo, forman parte sustancial de la concepción e implementación de una estrategia didáctica para el PEA de la Geometría Analítica en la AFAN, dirigida por uno de los autores en el contexto de la AFAN, no exenta de barreras u otras dificultades que pueden afectar el desarrollo exitoso de un PEA desarrollador.
Las carencias didácticas de los profesionales de la educación matemática en la AFAN rebasan las descritas en el presente artículo, como rebasan también los resultados de la aplicación de la citada estrategia didáctica en desarrollo, implementación y revisión.
Futuros trabajos en la propia institución universitaria del presente artículo o en otras universidades militares y civiles del país, deben continuar profundizando en lo que muchos estudiosos denominan ʹprofesionalización pedagógica del claustroʹ, para poder responder a las exigencias de la reforma universitaria emprendida en Angola desde el año 2005.
