ARTÍCULO ORIGINAL

 

 

Comportamiento autoafín de redes de drenaje controladas estructuralmente. Caso de estudio río San Cristóbal, Pinar del Río

 

 

Self-affine behavior of structurally controlled river networks. Case of study San Cristóbal river. Pinar del Río

 

 

 

Robert Ramírez Hernández¹, Dámaso Cáceres Govea¹

 

¹Universidad de Pinar del Río, Pinar del Río, Cuba [e-mail]

 

 

---

RESUMEN

Con la aplicación del análisis fractal a la red de drenaje del río San Cristóbal se pudo describir y cuantificar la complejidad de esta red y asociarla a las estructuras geológicas, fracturas y fallas presentes en el área. El análisis fractal autoafín permitió comprobar el desarrollo desigual de esta red en las direcciones longitudinal y transversal de las corrientes. El valor de la dimensión fractal promedio de las corrientes, bajo el supuesto de autoafinidad, es 1,04 indicando el predominio de corrientes rectas controladas tectónicamente, mientras que la dimensión fractal de la red, obtenida bajo condición de autosimilitud, toma valores de 1,59 y 1,47. Bajo el supuesto de autoafinidad, la dimensión de lagunaridad es igual a 1,86 y el coeficiente de Hurst 0,86 lo que muestra el acentuado control estructural sobre el drenaje. Las direcciones principales de las corrientes se asocian a las de zonas de debilidad creadas por el avance diferencial de los mantos durante los cabalgamientos o a las fracturas secundarias de Riedel, relacionadas con la transcurrencia de falla Pinar.

 Palabras clave: redes de drenaje; río San Cristóbal; fractales; autoafinidad; lagunaridad.

 

---

ABSTRACT

Geological structure influences the form, length and slope of rivers. An approach never used in the area is the fractal analysis for river networks, which allowed to describe and quantify the complexity of this network and associate it to geological structures and faults in the area. Self-similar fractal analysis allowed to prove the unequal river network development in longitudinal and transversal directions. The average fractal value, under self-similarity assumption, is 1,04, indicating the prevalence of straight superficial currents, tectonically controlled, while the river network fractal dimension takes values of 1,59 and 1,47. Under assumptions of self-affinity, the lacunarity dimension takes the value of 1,86 and the Hurst coefficient is 0,86, indicating the structural control on drainage. The main rivers directions coincide with zones of geological weaknesses, originated during the overthrust event, or secondary Riedel fractures related to the left-lateral movement of Pinar fault. 

Keywords: drainage nets; San Cristobal river; fractals; lacunarity; self-affine.

---

 

 

 

1. INTRODUCCIÓN

Las redes de drenaje son el resultado de la interacción compleja de los procesos geológicos y las condiciones climáticas que favorecieron el surgimiento del drenaje, que a su vez modela el relieve actual. Por lo tanto, en el relieve queda reflejada la evolución climática, hidrogeológica y geológica de la región donde se ha desarrollado la red de drenaje, a diferentes escalas espacio-temporales.

Estudios de las redes de drenaje, sus configuraciones y parámetros que describen su morfometría han aparecido publicados en los trabajos de Horton (1932, 1945); Strahler (1946); Schumm (1956); Hack (1957, 1973); y Rodríguez et al. (1991). Horton (1932, 1945) fue el primero en reconocer las características de invarianza de la red de drenaje al establecer las leyes de escala: relación de bifurcación (R_B), relación de longitud (R_L) y relación de área (R_A).

Los objetos naturales que poseen una estructura espacial compleja pueden estudiarse como fractales. Para el caso particular de las redes de drenaje dos dimensiones fractales pueden calcularse, una dimensión fractal promedio (d), que describe la sinuosidad de una corriente y la dimensión fractal de toda la red (D), relacionada con las características de ramificación o compacidad del sistema (La Barbera y Rosso 1989; Tarboton 1996). Según Schuller, Rao y Jeong (2001) la geometría fractal es útil para describir patrones irregulares y fragmentados. Estos patrones se repiten a diferentes escalas, de ahí el concepto de invarianza de escala o autosimilitud.

A partir del análisis entre la longitud de las corrientes y el área de las cuencas de drenaje Mandelbrot (1977) llegó a la conclusión que la dimensión fractal de cursos de agua independientes (d) era igual a 1,2; mientras que la dimensión fractal de todo el sistema (D) era igual o próximo a 2.

1.1. Fractales autosimilares

La autosimilitud de la red de drenaje puede establecerse en un inicio a partir del cálculo de parámetros morfométricos o leyes de las cuencas hidrográficas, establecidos por Horton (1932, 1945) y Schumm (1956), cuyas definiciones matemáticas son:

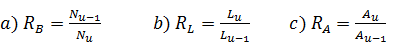                         (1)

donde R_B, R_L y R_A son la relación de bifurcación, la relación de longitud y la relación de área, respectivamente. 

Solo en pocas ocasiones estas leyes se cumplen estrictamente; esto se debe a que el desarrollo de redes estructuralmente hortonianas son raras en la naturaleza. Kirchner (1993) mostró que las leyes de invarianza al cambio de escala son estadísticamente inevitables en casi todas las redes y que no dependen de la estructura de la red. Este autor plantea que las leyes son una consecuencia del sistema jerárquico de ordenamiento de las corrientes creado por Strahler (1952) y que no necesariamente responden a una estructura fractal de la red.

La aplicación de las leyes de Horton se basa en el establecimiento de un sistema jerárquico de ordenamiento o clasificación de la red, entre los cuales el más utilizado es el establecido por Strahler (1952), según se muestra en la Figura 1.

 

La dimensión fractal de la corriente principal (D_s) (Ecuación 2), así como para toda la red (D_b) (Ecuación 3) se determinaron según Rosso, Bacchi y La Barbera (1991) y Liu (1992).

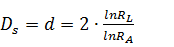                                                                   (2)

 

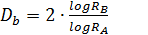                                                                       (3)

1.2. Características geológicas

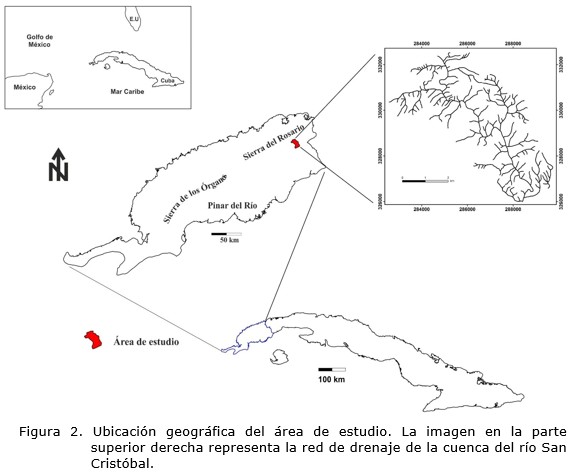
La cuenca del río San Cristóbal se ubica en la provincia Artemisa, Cuba occidental, entre los 22° 44’ 30.0’’ y 22° 49’ 0.0’’ de latitud norte, y los 83° 3’ 0.0’’ y 83° 7’ 0.0’’ de longitud oeste, con una superficie de 37 km² (Figura 2). Esta cuenca se ubica en la unidad de cabalgamientos de Sierra del Rosario/Alturas de Pizarras del Norte/Esperanza definida por Cobiella (2008).

En los últimos años se han realizado trabajos de detalle para precisar las características estructurales del corte de la parte oriental de la Sierra del Rosario y esclarecer aspectos relacionados con la orogenia cubana, así como con movimientos neotectónicos, en especial, relacionados con falla Pinar (Cofiño y Cáceres 2003; Ordaz 2013; Ordaz et al. 2013).

Estos estudios han estado dirigidos al análisis microtectónico y a la observación de indicadores cinemáticos para reconstruir la dirección de los esfuerzos máximos horizontales, principales responsables de la evolución de las morfoestructuras actuales.

 

Hasta el presente no se conoce ningún trabajo en nuestro país que aborde los estudios fractales de las redes de drenaje, ni la vinculación que estas redes poseen con la estructura geológica de las áreas donde se desarrollan. Es por ello que se aplica la teoría de los fractales autosimilares y autoafines a la resolución de este problema, además de realizar un estudio de las principales direcciones de los lineamientos presentes en el área y su comparación con las direcciones de las corrientes de diferentes órdenes.

2. MATERIALES Y MÉTODOS

2.1. Extracción de la red de drenaje

La extracción de la red de drenaje se realizó de forma manual, sobre las hojas cartográficas San Cristóbal y Soroa, escala 1:25 000. Esta red se clasificó siguiendo el método propuesto por Strahler (1952). Para determinar la longitud euclidiana de las corrientes se determinaron los puntos iniciales y finales de cada segmento. El área de drenaje de cada río fue digitalizada utilizando como base las hojas cartográficas antes mencionadas, así como el modelo de elevación digital escala 1:25 0000. Con estos parámetros se construyeron los gráficos utilizados en la determinación de las características fractales de la cuenca.

2.2. Cálculo de la dimensión fractal

Nikora y Sapozhnikov (1993) y Nikora, Ibbitt y Shankar (1996) plantean que la mayoría de las redes de drenaje no son autosimilares, por lo que extienden el desarrollo de la teoría de las redes fractales autosimilares hacia las redes fractales autoafines. Según estos autores existen dos exponentes de escala: uno en la dirección longitudinal y otro en la dirección transversal de la red. Para la determinación de los exponentes de escala establecen las relaciones entre los tamaños característicos longitudinal (Ecuación 4a) y transversal (Ecuación 4b) del drenaje con respecto a la longitud total de las corrientes Z, además de formular la relación entre el tamaño característico longitudinal de la cuenca y la longitud de una corriente principal (Ecuación 4c).

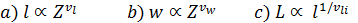                             (4)

En estas ecuaciones V_l y V_w representan los exponentes de escala en las direcciones longitudinal y transversal, V_li = V_l, respectivamente, al tiempo que l y w son los tamaños característicos de la red en las direcciones mencionadas; de forma práctica estos exponentes de escala se calculan:

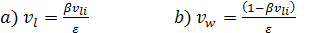                                        (5)

En el caso de V_li debe probarse, mediante gráficos logarítmicos de longitud euclidiana vs longitud real de las corrientes, la hipótesis que plantea que las corrientes a escalas pequeñas son autosimilares (Sapozhnikov y Nikora 1993; Nikora, Ibbitt y Shankar 1996). Si los exponentes V_l y V_w son iguales la red es autosimilar, de lo contrario se plantea que la red es autoafín. En el caso en el cual ambos exponentes son diferentes la dimensión fractal es reemplazada por la dimensión de lagunaridad (D_G), la cual se obtiene como:

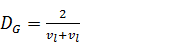                                                                     (6)

Nikora y Sapozhnikov (1993) interpretaron la relación V_w/V_l como el exponente de Hurst, H, de acuerdo a lo sugerido por Mandelbrot (1986). El exponente de Hurst caracteriza el grado de autoafinidad de la red; mientras más alejado de 1, más autoafín es la red. Con el propósito de establecer una comparación entre los valores fractales promedio para las corrientes y para la red, la dimensión fractal es estimada por otros métodos recogidos en la literatura. Rosso, Bacchi y La Barbera (1991) proponen para una corriente:

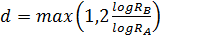                                                      (7)

La Barbera y Rosso (1990) derivan una nueva expresión para el cálculo de la dimensión fractal de toda la red:

                                                           (8)

3. RESULTADOS

La Tabla 1 recoge los parámetros morfométricos de la red de drenaje descritos por las ecuaciones 1a)-1c). Se muestran, además, los intervalos en los que deben variar estos parámetros y el valor más común.

Como puede apreciarse los valores de los índices morfométricos se ubican en los intervalos probables, con la excepción de R_A, el cual excede ligeramente los valores promedios observados en la mayoría de las cuencas reportadas por varios autores. Corrientes de orden 1 de grandes longitudes, también una de las corrientes de orden 4, y las pequeñas áreas de las subcuencas de los ríos de estos órdenes son las razones que justifican el valor elevado de R_A.

3.1. Valor fractal bajo supuesto de autosimilitud

La dimensión fractal para las corrientes individuales fue estimada según Takayasu (1990), Rosso, Bacchi y La Barbera (1991) y Liu (1992). Los valores obtenidos por cada uno de los métodos fueron: 1,04, 1,47 y 0,96. Cabe recordar que los dos últimos autores consideran las redes de drenaje como autosimilares y por lo tanto emplean los coeficientes de Horton para el cálculo de la dimensión fractal, a diferencia del primer autor quien se basa en las longitudes real y euclidiana de las corrientes. Hack (1957) calculó la dimensión fractal de las corrientes en las cuencas de los ríos Virginia y Maryland, encontrando d igual a 1,2. Este autor también realizó cálculos para cuencas en el oeste de los Estados Unidos y encontró un valor promedio de 1.4, llegando a la conclusión que d variaba de región a región.

La dimensión fractal de la red se estimó empleando todos los valores de d, con el propósito de comparar el efecto de las variaciones de este parámetro sobre D. Los valores obtenidos mediante la Ecuación 8, según La Barbera y Rosso (1990), son: 1,59; 2,87 y 1,47. El valor de 2,87 no es posible, debido a que el valor fractal máximo de una red que se comporta como un modelo topológico aleatorio es igual a 2. Los valores de 1,59 y 1,47 pueden considerarse similares, pues el rango de variación es 0,12. Se aprecia en los estimados de D la importancia del método de cálculo de la dimensión fractal promedio de las corrientes, d. Entonces, se puede asumir que la dimensión fractal para la red es 1,53, la cual es el promedio de 1,59 y 1,47.

3.2. Valor fractal bajo supuesto de autoafinidad

Nikora y Sapozhnikov (1993) y Nikora, Ibbitt y Shankar (1996) no consideran las redes de drenaje como objetos naturales autosimilares sino autoafines. O sea, que consideran que ocurren cambios de escala en las direcciones longitudinal y transversal de las corrientes. Esta definición, en opinión de los autores de este trabajo, se ajusta más a las condiciones en las cuales se desarrollan las redes de drenaje. Para calcular la dimensión de lagunaridad (D_G) por este método es necesario determinar los exponentes característicos transversal y longitudinal de toda la red, lo que se realiza gráficamente (Figura 3).

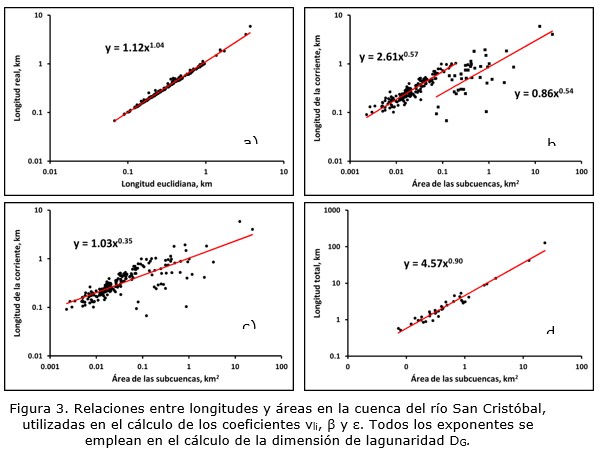
La dimensión fractal promedio, d, es igual a 1,04, Figura 3a). La Figura 3b) describe la relación entre el área drenada por cada corriente principal y la longitud de la misma. Los ríos de orden 1, representadas con puntos, han sido separados de los ríos de orden superior, y la recta ajustada posee una pendiente β = 0,57. El valor de la pendiente β para las corrientes de orden 2 en adelante es 0,54. La pendiente de la recta β para todas las corrientes es 0,35, Figura 3c). La Figura 3d) expresa la relación entre la suma de las longitudes de cada corriente y el área de drenaje de cada subcuenca que encierra estas corrientes, ε = 0,90.

4. DISCUSIÓN

4.1. Comportamiento autoafín

La dimensión de lagunaridad, independientemente de los valores de β utilizados en el cálculo, es igual a 1,80. Sin embargo, el efecto de β es particularmente importante en el cálculo de los parámetros de escala en las direcciones longitudinal, v_l, y transversal, v_w. Para β = 0,54 los valores de v_l y v_w son 0,60 y 0,51, y el coeficiente de Hurst H_lw = 0,86, confirmando la presencia de una red autoafín. Sin embargo, para β = 0,35 los valores de v_l y v_w son 0,39 y 0,72 y H_lw = 1,83, lo cual es un valor anómalo. Este valor anómalo pudiera estar dado porque la red se comporta como multifractal en lugar de fractal. Con el propósito de comparar los resultados obtenidos en este trabajo y otros lugares del mundo se incluye la Tabla 2.

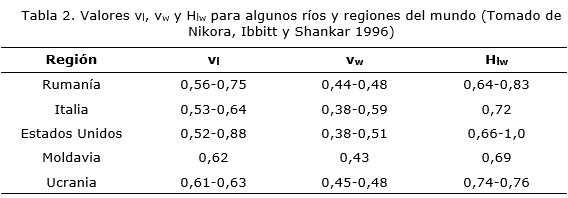
Como puede observarse los valores calculados para el río San Cristóbal caen en el rango de valores obtenidos para otras cuencas en varias regiones el mundo. Corrientes principales encajadas en sus cauces, con pendientes elevadas a ambos lados y un medio geológico, con predominio de rocas carbonatadas, hacen que se violen sistemáticamente las leyes de Horton sobre la composición del drenaje. Estas condiciones acentúan el carácter autoafín de la red de drenaje del río San Cristóbal, aunque no queda totalmente claro porqué las corrientes de orden 1 se desplazan hacia la izquierda en el gráfico de la Figura 3b), con respecto al resto de las corrientes de orden superior.

4.2. Análisis tectono-estructural del drenaje

Como bien puede apreciarse en la Figura 1, la red de drenaje del río San Cristóbal se caracteriza por la presencia de corrientes rectas, paralelas, subparalelas y con cambios bruscos de dirección, además, es frecuente observar intercepciones entre ellos formando ángulos cercanos a los 90º, todo lo cual apunta al control tectónico y estructural sobre el drenaje. Las corrientes de orden 4 y 5 tienen una dirección preferencial NW-SE, Figura 4b), siguiendo la dirección de fallas de gran magnitud que, según Cofiño y Cáceres (2003), son el resultado del avance diferencial de los mantos durante los cabalgamientos.

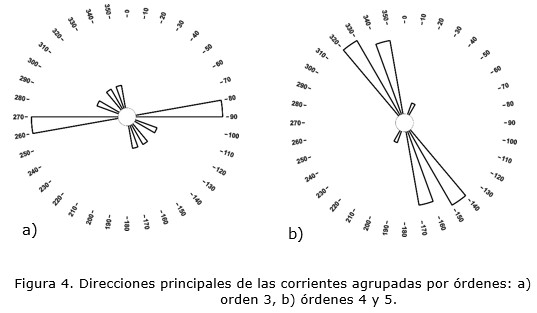
Sin embargo, las corrientes de orden 3 (Figura 4a) muestran una dirección predominante al E, asociadas directamente a las fracturas primarias de Riedel; mientras que las corrientes de orden 1 y 2 varían indistintamente y se alinean principalmente de acuerdo a las fracturas secundarias de Riedel (Figuras 5a y 5b).

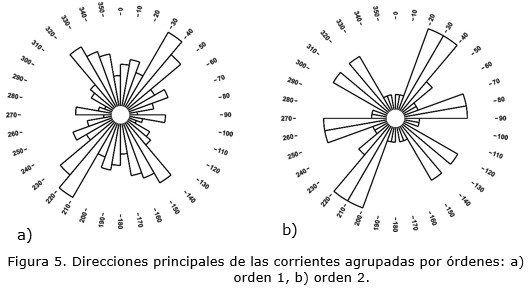
La coincidencia entre las direcciones de los alineamientos y las direcciones de las corrientes superficiales confirma el predominio de la estructura sobre la litología en el desarrollo de la red de drenaje.

5. CONCLUSIONES

· Los valores de la dimensión fractal de las corrientes: 1,04 y 1,47 caen en el rango de valores observados en otras cuencas del mundo. El valor 0,96 pudiera deberse a que las leyes de Horton no se comportan invariables en la cuenca. Se asume 1,04 como valor real para d, ya que su cálculo no depende de supuestos, sino de las longitudes real y euclidiana de las corrientes. La dimensión fractal promedio de la red de drenaje, bajo condición de autosimilitud es igual a 1,53. El valor D igual a 2,87 es un valor anómalo, para el cual, con el grado de estudio actual, no existe explicación práctica.

· Considerar la red como autoafín ofrece mejores resultados, no solo al producir un valor D_G igual a 1,86, más próximo a 2, sino por la posibilidad de calcular el coeficiente de Hurst y obtener un estimado del grado de autosimilitud, el cual es 0,86. El desplazamiento de las corrientes de orden 1 respecto al resto en el gráfico de longitud vs área aún carece de fundamentación, por lo que se requieren nuevos estudios en este sentido. Las direcciones de las corrientes de diferentes órdenes responden en primer lugar al patrón de fracturas creadas durante los cabalgamientos y en segundo lugar a las fracturas Riedel que se originaron como consecuencia de la rotación del máximo estrés compresivo.

6. REFERENCIAS

Cobiella, J. L. 2008: Reconstrucción palinspástica del paleomargen mesozoico de América del Norte en Cuba occidental y el sudeste del Golfo de México. Implicaciones para la evolución del SE del Golfo de México. Revista Mexicana de Ciencias Geológicas 25(3): 382-401.

Cofiño, C. E. y Cáceres, D. 2003: Efectividad de la utilización de métodos microtectónicos en el desciframiento de la evolución de estructuras tectónicas (Falla Pinar). Minería y Geología 19(3-4): 29-34.

Hack, J. T. 1957: Studies of longitudinal stream profiles in Virginia and Maryland. U.S. Geological Survey, Professional Paper 294: 45-97.

Hack, J. T. 1973: Stream-profile analysis and stream-gradient index. U.S. Geological Survey, Journal Research 1(4): 421-429.

Horton, R. E. 1932: Drainage basin characteristics. Transactions American Geophysical Union 13(1): 350-361.

Horton, R. E. 1945: Erosional development of streams and their drainage basins: hydrophysical approach to quantitative morphology. Geological Society America Bulletin 56(3): 275-370.

Kirchner, J. W. 1993: Statistical inevitability of Horton's laws and the apparent randomness of stream channel networks. Geology 21: 521-594.

La Barbera, P. y Rosso, R. 1989: On the fractal dimension of stream networks. Water Resources Research 25(4): 735-741.

La Barbera, P. y Rosso, R. 1990: Reply. Water Resources Research 26(9): 2245–2248.

Liu, T. 1992: Fractal structure and properties of stream networks. Water Resources Research 28(11): 2981-2988.

Mandelbrot, B. B. 1977: Fractals, form, chance and dimension. W. W. Freeman and Company, San Francisco.

Mandelbrot, B. B. 1986: Self-affine fractal sets. En: Pietronero, L. y Tosatti, E. (Eds.). Fractals in Physics. North-Holland, Amsterdam.

Nikora, V. I. y Sapozhnikov, V. B. 1993: River network fractal geometry and its computer simulation. Water Resources Research 29(10): 3569-3575.

Nikora, V.; Ibbitt, R. y Shankar, U. 1996: On channel network fractal properties: A case of study of the Hutt River basin, New Zealand. Water Resources Research 32(11): 3375-3384.

Ordaz, A.; Hernández, J. R.; Cofiño, C. E.; Méndez, A. P. y Galaz, G. 2013: Análisis estructural y morfotectónico en los municipios San Cristóbal y Candelaria, Cuba Occidental: contribución a los estudios de peligrosidad sísmica de la falla Pinar. Investigaciones Geográficas, Boletín del Instituto de Geografía, UNAM (82): 7-23.

Ordaz, A. 2013: Evaluación de las condiciones ingeniero-geológicas para el pronóstico de la respuesta dinámica de los suelos. Caso de estudio: Ciudad de San Cristóbal, Cuba occidental. Tesis de doctorado. Universidad de Pinar del Río.

Rodríguez, I.; Rinaldo, A.; Rigon, R.; Bras, R. L.; Marani, A. y Ijjász, E. 1991: Energy dissipation, runoff production, and the three-dimensional structure of river basins. Water Resources Research 28(4): 1095-1103.

Rosso, R.; Bacchi, B. y La Barbera, P. 1991: Fractal relation of mainstream length to catchment area in river networks. Water Resources Research 27(3): 381-387.

Schuller, D. J.; Rao, A. R. y Jeong, G. D. 2001: Fractal characteristics of dense stream networks. Journal of Hydrology 243: 1–16

Schumm, S. A. 1956: Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey. Geological Society of America Bulletin 67: 597-646.

Strahler, A. N. 1946: Elongate intrenched meanders of Conodoguinet Creek. American Journal of Science 244(1): 31-40.

Strahler, A. N. 1952: Dynamic basis of geomorphology. Geological Society of America Bulletin 63: 923–938.

Takayasu, H. 1990: Fractals in the physical sciences. Manchester University Press, Manchester.

Tarboton, D. G. 1996: Fractal river networks, Horton's laws and Tokunaga cyclicity. Journal of Hydrology 187(1-2): 105-117.

 

 

 

Recibido: 30/11/2016
Aprobado: 23/02/2017

 

 

 

Robert Ramírez Hernández, Máster en Ciencias. Profesor Auxiliar. Universidad de Pinar del Río, Cuba [e-mail]