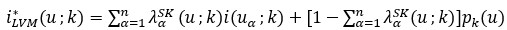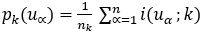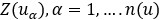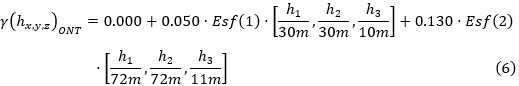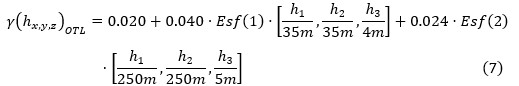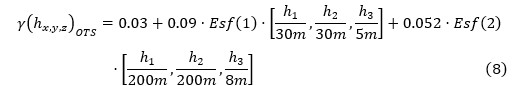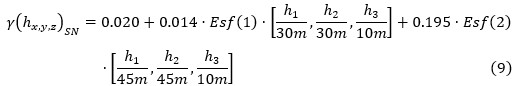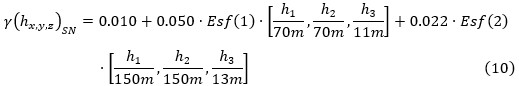Artículo Original

Modelaje probabilístico y cuantificación de la incertidumbre de los horizontes de la corteza de meteorización del depósito de níquel San Felipe

Probabilistic modeling and uncertainty quantification of weathering crustal horizons of San Felipe nickel deposit

0000-0001-6879-4626José Alberto Arias-del Toro^{1  *}  , 0000-0002-6841-8086Alain Carballo-Peña²  , 0000-0001-7311-8382Elmidio Estévez-Cruz³  , 0009-0004-1178-3781Rosa María Cobas-Botey¹ 

¹Oficina Nacional de Recursos Minerales, La Habana, Cuba.

²Universidad de Moa, Holguín, Cuba.

³Universidad de Pinar del Río, Pinar del Río, Cuba.

RESUMEN

Aunque el modelaje geológico comúnmente realizado en los depósitos minerales es del tipo determinístico, la modelación probabilística resulta más adecuada para conocer o medir cuantitativamente la incertidumbre asociada. El objetivo del presente trabajo fue cuantificar, para un sector del depósito de níquel San Felipe, la incertidumbre de los horizontes de la corteza de meteorización a partir de su modelación probabilística. Como base se tomó el modelo geológico descriptivo del depósito laterítico, caracterizado por la zonalidad litológica en profundidad. Se empleó la técnica probabilística de simulación secuencial Indicador con Proporciones Localmente Variables, mediante la cual se reproducen sintéticamente 50 escenarios equiprobables de las unidades geológicas, condicionadas a 3 884 compósitos de la red de pozos de 100 m x 100 m. Como resultado se presenta para el sector de estudio el modelo 3D de los horizontes litológicos en soporte de bloques, así como los mapas de entropía que cuantifican la incertidumbre asociada al modelo de las unidades geológicas modeladas. Se concluye que, dada la variabilidad presente en este tipo de depósito laterítico, la disponibilidad de información geológica resulta aún insuficiente para reproducir con un nivel de certidumbre adecuado el modelo de los horizontes de la corteza de meteorización.

Palabras-clave: depósito San Felipe; modelo probabilístico; simulación secuencial; cuantificación de incertidumbre; entropía condicional

ABSTRACT

The geological modeling commonly performed on mineral deposits is of the deterministic type, but it has been demonstrated that probabilistic modeling is more adequate to know or quantitatively measure the associated uncertainty. This study is aim to quantify the uncertainty of weathering crustal horizons for a sector of the San Felipe nickel deposit, based on its probabilistic modeling. The descriptive geological model of the lateritic deposit was taken as a basis, characterized by the lithological zoning at depth. The probabilistic Sequential Indicator Simulation with Locally variable Proportions was used, through which 50 equiprobable scenarios of the geological units are synthetically reproduced, conditioned to 3,884 composites from the network of 100 m x 100 m drillholes. As a result, the 3D model of the lithological horizons on block support is presented for the study sector, as well as the entropy maps that quantify the uncertainty associated with the model of the modeled geological units. As conclusion, we can say that, due to the variability present in this type of lateritic deposit, the availability of geological information is still insufficient to reproduce the model of weathering crust horizons with an adequate level of certainty.

Key words: San Felipe deposit; probabilistic model; sequential simulation; uncertainty quantification; conditional entropy

INTRODUCCIÓN

El modelaje geológico que comúnmente se realiza en los depósitos minerales es de tipo determinístico, en el que se asume el conocimiento geométrico perfecto de la forma y el tamaño de las unidades geológicas modeladas, constituyendo así la única representación de la realidad desconocida. Dado que los depósitos minerales son inherentemente heterogéneos a todas las escalas, la modelación probabilística resulta más adecuada cuando se necesita conocer o medir cuantitativamente la incertidumbre asociada de las unidades geológicas que se modelan.

En los depósitos lateríticos, la modelación geológica determinística se realiza comúnmente mediante la creación de superficies de triangulación que delimitan los diferentes horizontes litológicos (^{Horton y Lipton 2002}; ^{Elias et al. 2018}), las cuales son creadas por algún tipo de algoritmo de interpolación: Delaunay (^{Xue, Sun y Ma 2004}); Laplace (^{Gemcom Software International Inc. 1998}; ^{Hughes y Cameron 2012}); Krigeaje (^{Ilyas y Koike 2012}; ^{Jia, Li y Che 2020}); Funciones Radiales Básicas por modelamiento implícito (^{Cowan et al. 2003}; ^{Kenworthy 2015}) y otros, cuyos modelos son aceptables cuando el nivel de información resulta adecuado. Sin embargo, cuando la densidad de muestreo es insuficiente, el uso de las técnicas de modelación probabilística tales como las simulaciones geoestadísticas condicionales (^{Dagasan et al. 2019}) ofrecen el acceso al conocimiento del nivel de incertidumbre en que se incurre al considerar varios escenarios equiprobables, permitiendo así manejar el riesgo asociado.

El objetivo del presente trabajo fue cuantificar la incertidumbre de la distribución espacial de los horizontes simulados de la corteza de meteorización en un sector del depósito de níquel San Felipe, usando la técnica probabilística, según varios escenarios equiprobables, discretizados en paneles de 25m x 25m x 1m y usando la entropía como medida del desorden o difusión espacial y de la cantidad de información contenida en tales modelos simulados (^{Journel y Deutsch 1993}; ^{Wellmann y Regenauer-Lieb 2012}; ^{Hansen 2020}; ^{Mizuno y Deutsch 2022}).

Caracterización geológica del sector

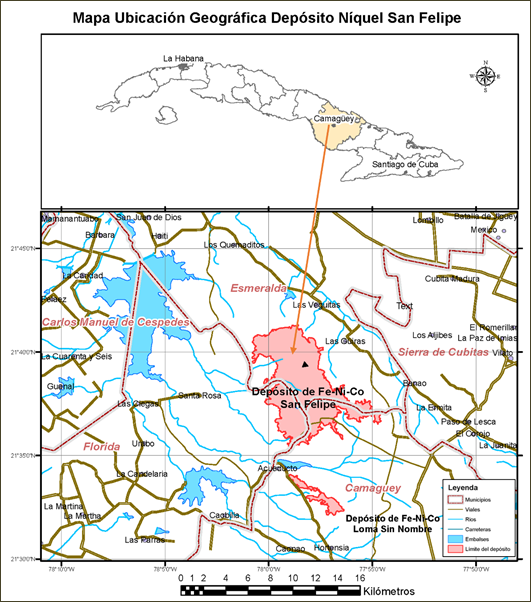
El sector bajo estudio se localiza en una pequeña área del sector sureste (^{Horton y Lipton 2002}) del depósito de níquel San Felipe, en la provincia de Camagüey, Cuba (Figura 1). En el área se desarrolla una corteza de meteorización de tipo manto lineal, de edad terciaria (^{Cobas-Botey, Formell-Cortina y Leyva-Rodríguez 2017}), con alto contenido de sílice (^{Chang-Rodríguez y Rojas-Purón 2018}), formada a partir de rocas ultramáficas, principalmente harzburgitas serpentinizadas; subordinadamente aparecen además cúmulos máficos, diques paralelos de diabasa y basaltos oceánicos (^{Rodríguez-Catalá y Rodríguez-Infante 2021}).

Las menas niquelíferas son esencialmente de composición arcillosa esmectítica silicatada, denominándose también como de tipo arcilla (^{Gallardo et al. 2010}; ^{Cobas-Botey, Formell-Cortina y Leyva-Rodríguez 2017}).

Figura 1 Mapa de ubicación geográfica del depósito de níquel San Felipe. 

El perfil de la corteza de meteorización que se desarrolla en el depósito de níquel San Felipe presenta una zonación transicional formada por seis horizontes, según ^{Cobas-Botey (2017}) como se muestra en la Tabla 1.

Tabla 1 Descripción del perfil de la corteza de meteorización 

Para la modelación geoestadística se agruparon como una sola unidad los horizontes de los ocres no texturales con perdigones (ONTCP) y los ocres no texturales sin perdigones (ONT), denominándose simplemente como ocres no texturales (ONT). Dada la cantidad de compósitos, el resto de los horizontes de la corteza de meteorización se mantuvo como describe ^{Cobas-Botey (2017}), siendo los horizontes de este estudio los cinco siguientes: ONT, OTL, OTS, SN y SL.

MATERIALES Y MÉTODOS

Para simular los horizontes de la corteza de meteorización en el sector de estudio, el método geoestadístico usado fue la Simulación Secuencial Indicador con Proporciones Localmente Variables; se basa en el estimador krigeaje indicador simple no estacionario con medias (proporciones) variables, usado para determinar el valor de la función de probabilidad condicional discreta (FPCD) a partir de la cual se estableció el horizonte correspondiente, empleando la profundidad y(u) como variable secundaria.

El estimador krigeaje indicador simple no estacionario con proporciones localmente variables (^{Goovaerts 1997}; ^{Deutsch 2006}; ^{Mizuno y Deutsch 2022}) se expresa en la ecuación 1:

(1)

Donde:

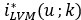- Estimador de la proporción localmente variable del horizonte k en la localización u.

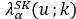- Pesos o ponderadores del krigeaje, obtenidos mediante la resolución del sistema de ecuaciones de krigeaje simple.

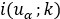- Variable indicador binaria, igual a 1 si el horizonte k prevalece en la localización u, e igual a cero en caso contrario.

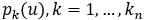, Proporción o probabilidad media condicional del horizonte 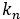en el intervalo de profundidad 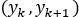y se obtiene a partir de la expresión 2:

(2)

Donde:

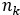cantidad de individuos del horizonte k en el intervalo de profundidad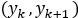

La simulación se realizó usando el programa BLOCKSIS (^{Deutsch 2006})

Descripción del algoritmo de la Simulación Secuencial Indicador con Proporciones Localmente Variables

• Creación de una red de nodos a simular en el espacio tridimensional.

• Definición de un camino aleatorio a través de la red de nodos. Y en cada nodo:

• Recuperación de los datos condicionantes cercanos al nodo a simular

• 

• Conversión de cada dato condicionante recuperado 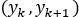en un vector de indicadores:

• 

• Estimación de la probabilidad condicional para cada uno de los horizontes, a partir de la variable indicadora 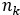, mediante el sistema de krigeaje indicador simple no estacionario con media variable, igual a la proporción .

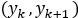• Corrección de los problemas de las relaciones de orden y determinación del valor de la función de probabilidad condicional discreta (FPCD)

• 

• Extracción de la categoría a partir de la FPCD y asignarla como dato a la localización .

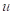• Remplazo en cada localización, del horizonte simulado por el del horizonte más probable en la vecindad local, evitando de esta manera que las variaciones a pequeña escala reproduzcan comportamientos geológicos no realistas.

Los pasos precedentes se repiten para generar otra realización.

Entropía condicional como medida de la incertidumbre de los horizontes de la corteza de meteorización

La entropía condicional (^{Babak, Manchuk y Deutsch 2013}) se utiliza como medida de incertidumbre de los horizontes de la corteza de meteorización, la cual se asocia al grado de mezcla de aquellos dentro de un mismo bloque o panel de estimación, y se calcula a partir de las proporciones de los horizontes de la corteza de meteorización localizados dentro de un bloque o celda (^{Shannon 1948}; ^{Journel y Deutsch 1993}; ^{Larrondo 2003}; ^{Mizuno y Deutsch 2022}) mediante la expresión 3:

(3)

Las proporciones 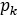se calculan a partir de la expresión 4:

(4)

Donde 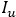es el horizonte en la localización espacial u y n el número de horizontes, según la expresión 5.

(5)

Ello significa que cuando la probabilidad o proporción de los horizontes involucrados en una misma celda o bloque es igual o aproximada, la entropía condicional se maximiza, por ende, el grado de incertidumbre es máximo; por el contrario, cuando un tipo determinado de horizonte prevalece, la entropía es cero, por tanto, el grado de incertidumbre del horizonte asignado al bloque o celda es mínimo. En los otros casos, la entropía condicional se sitúa entre estos dos casos extremos (^{Babak, Manchuk y Deutsch 2013}).

Procedimiento para el modelaje y la cuantificación de la incertidumbre de los horizontes de la corteza de meteorización en el sector caso de estudio

1. Creación de un fichero de 3 884 compósitos con la información de los horizontes de la corteza de meteorización regularizada a un metro, con espaciamiento predominante de 100m x 100m x 1m; subordinadamente con espaciamientos de 50m x 50m x 1m, 25m x 25m x 1m y 12,5m x 12,5m x 1m.

2. Despliegue de los compósitos mediante la técnica Unwrinkling (^{Richmond 2013}; ^{Gray et al. 2022}) usando como superficie de despliegue el modelo de elevación digital (MED), haciendo corresponder a un mismo nivel de elevación (cota), los horizontes de la corteza de meteorización, tomando en cuenta su naturaleza ondulante.

3. Cálculo de las indicatrices binarias y de las proporciones medias según la profundidad de los horizontes de la corteza de meteorización.

4. Análisis estructural. Cálculo de los semi-variogramas direccionales de las indicatrices binarias de los horizontes de la corteza de meteorización, análisis de anisotropía y ajuste a modelos teóricos.

5. Simulación puntual de los horizontes de la corteza de meteorización por el método de Indicatrices con proporciones Localmente variables en espaciamiento de 5m x 5m x 1m para 50 escenarios equiprobables. Validación.

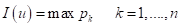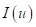6. Escalado a paneles de 25m x 25m x 1m. Cálculo de las probabilidades medias por horizonte, asignación a cada panel del horizonte más probable, lo que Babak, Manchuk y Deutsch (2013) denominan como voto mayoritario según: donde es el horizonte en la localización espacial 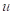y 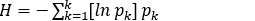el número de horizontes; y su correspondiente valor de entropía 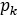, usando las simulaciones puntuales de los horizontes de la corteza de meteorización simulados en el paso E.

7. Creación de los mapas y los modelos 3D de entropía 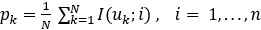de los horizontes de la corteza de meteorización regularizados sobre el plano horizontal.

8. Cuantificación de la incertidumbre de los horizontes de la corteza de meteorización, a partir de los valores medios de entropía 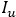estimados.

RESULTADOS

Cálculo de las proporciones medias de los horizontes de la corteza de meteorización según intervalos de profundidad

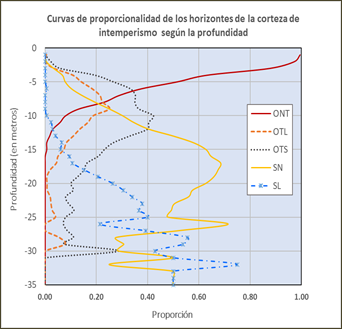
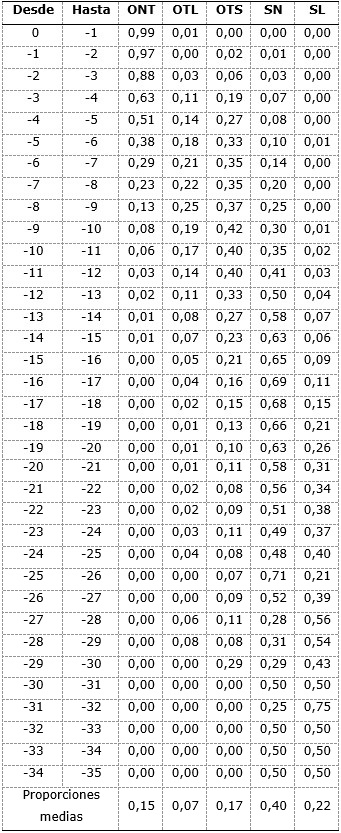
Las proporciones medias de los horizontes de la corteza de meteorización por intervalos de profundidad (Tabla 2) se obtuvieron mediante el promedio de los valores indicadores binarios [0,1] que revelan la presencia o ausencia del horizonte en el intervalo dado, usando la expresión 2. Las proporciones medias calculadas representan los valores de probabilidad a priori de los horizontes según la profundidad, a partir de los cuales se construyeron las curvas de proporcionalidad de los horizontes de la corteza de meteorización según la profundidad (Figura 2).

Tabla 2 Proporciones medias calculadas de los horizontes de la corteza de meteorización, según los intervalos de profundidad 

Figura 2 Curvas de proporcionalidad de los horizontes de la corteza de meteorización según la profundidad. 

Cálculo y ajuste de los semi-variogramas direccionales indicadores de los horizontes de la corteza de meteorización

El cálculo de los semi-variogramas experimentales indicadores se realizó tomando en consideración la disposición espacial de los horizontes de la corteza de meteorización, en el plano XY, según las direcciones 0⁰, 45⁰, 90⁰ y 135⁰, así como perpendicular a este plano (-90⁰ hacia abajo), siendo para la dirección horizontal con un espaciamiento (lag) de 25m y para la dirección vertical de un metro, ambas con tolerancia angular de 22.5⁰.

Se ajustaron modelos teóricos autorizados que representan las funciones estructurales que rigen el comportamiento de la continuidad espacial de cada uno de los horizontes antes mencionados en los límites del sector de estudio (Figura 3).

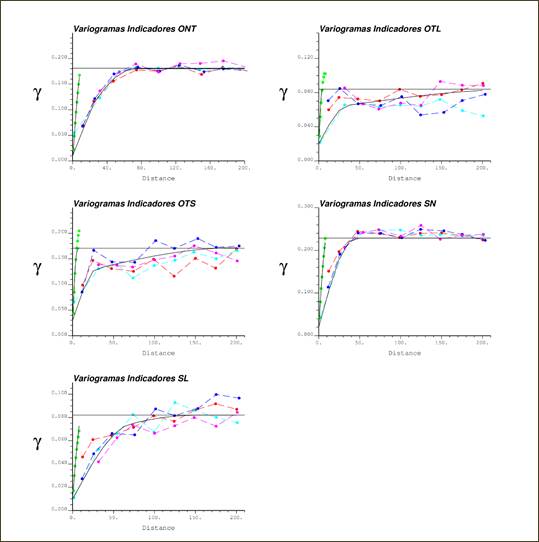
Figura 3 Semi-variogramas experimentales Indicadores de los horizontes de la corteza de meteorización, ajustados. Simbología: rojo 0⁰; azul claro 45⁰; azul 90⁰; púrpura 135⁰; verde dirección vertical. 

Las funciones estructurales ajustadas a los semi-variogramas indicadores experimentales de los horizontes de la corteza de meteorización en los límites del sector de estudio son expresadas en 6, 7, 8, 9 y 10:

Ocres No Texturales (ONT)

(6)

Ocres Texturales Limoníticos (OTL)

(7)

Ocres Texturales Saprolíticos (OTS)

(8)

Serpentinitas Nontronizadas (SN)

(9)

Serpentinitas Lixiviadas (SL)

(10)

Simulación Secuencial Indicador con Proporciones Localmente Variables

La simulación por el método de Simulación Secuencial Indicador con Proporciones Localmente Variables se realizó para simular los horizontes de la corteza de meteorización a través del algoritmo expuesto en el epígrafe 2.1, utilizando las funciones estructurales anteriormente enunciadas, así como los valores de las proporciones medias calculadas según los intervalos de profundidad (medias variables no estacionarias), realizándose en una red puntual de nodos con espaciamiento de 5m x 5m x 1m, para 50 escenarios equiprobables.

Validación de los escenarios simulados

Para validar los escenarios simulados se usaron los siguientes criterios:

1. condicionamiento espacial de los datos (^{Echeverri-Londoño 2016}) realizado mediante la comparación visual para el chequeo de la correspondencia espacial de los horizontes de la corteza de meteorización con los compósitos usados como datos condicionantes para realizar la simulación (Figura 4);

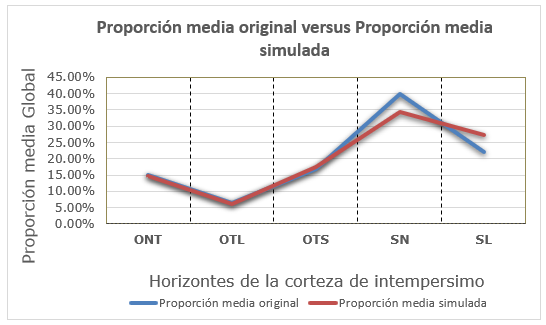
2. reproducción de las proporciones medias de los horizontes según los intervalos de profundidad (Figura 5);

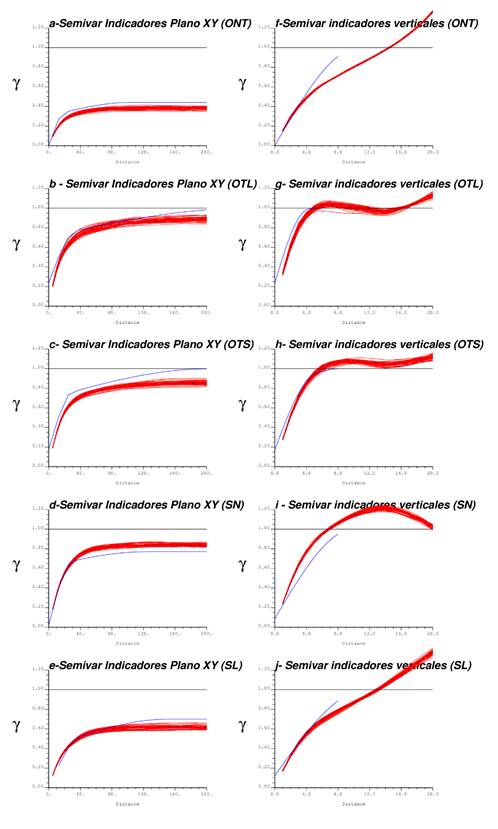
3. comparación de las curvas de los semi-variogramas indicadores simulados con las curvas de sus modelos teóricos ajustadas a los semi-variogramas indicadores experimentales de los datos reales (Figura 6).

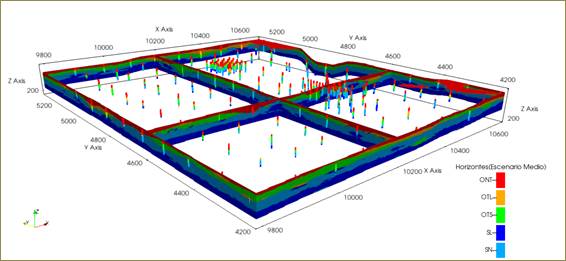
Figura 4 Escenario medio simulado de los horizontes de la corteza de meteorización en red puntual de 5m x 5m x 1m versus compósitos usados en la simulación. 

Figura 5 Representación de las proporciones media y simulada para 50 escenarios equiprobables. 

Figura 6 Semi-variogramas indicadores simulados 50 escenarios (líneas rojas) versus modelos teóricos ajustados (líneas en azul). 

Modelo de los horizontes de la corteza de meteorización en paneles de 5m x 5m x 1m

El modelo 3D de los horizontes de la corteza de meteorización en los paneles de 5m x 5m x 1m (Figura 7) se realizó mediante el cálculo de las proporciones (probabilidades) de cada horizonte dentro del panel, asignándole a este el horizonte con mayor proporción utilizando, como dato de entrada, los horizontes simulados a escala puntual en la red de nodos de 5m x 5m x 1m, para los 50 escenarios equiprobables, en base a la expresión 4.

Figura 7 Modelo de los horizontes de la corteza de meteorización en celdas 5m x 5m x 1m y compósitos usados como datos de entrada de la simulación. 

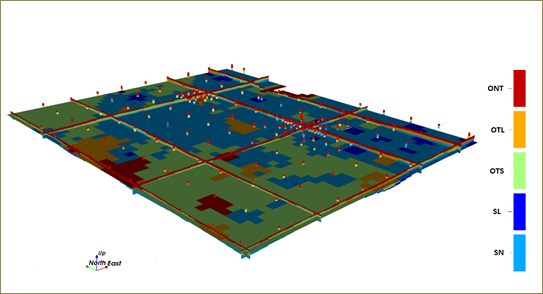
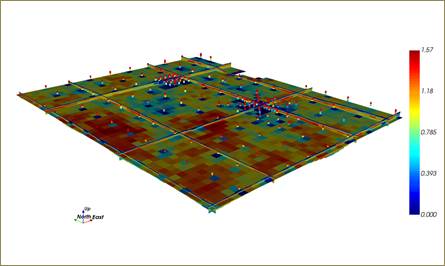
Modelo 3D de la entropía condicional en paneles de 25m x 25m x 1m

El modelo 3D de la entropía condicional de cada uno de los paneles de 25m x 25m x 1m (Figura 8), fue determinada utilizando los valores de las proporciones medias calculadas de cada horizonte de la corteza de meteorización, mediante la expresión 3.

Figura 8 Modelo de entropía condicional 3D en celdas 25m x 25m x 1m y de los compósitos de entrada a la simulación. 

Mapas de entropía condicional de los horizontes de la corteza de meteorización e histogramas de frecuencia y estadígrafos de entropía condicional

Los mapas de entropía condicional de los horizontes de la corteza de meteorización (Figura 9) fueron creados promediando los valores de entropía condicional del modelo 3D en cada celda de 25m x 25m, sobre el plano X-Y, con el objetivo de visualizar la variaciones y comportamiento espacial de este parámetro de forma independiente para cada horizonte de la corteza de meteorización sobre ese plano.

Con el propósito de realizar una descripción estadística de la entropía por horizontes se construyeron, además, los histogramas de frecuencia y se calcularon los estadígrafos correspondientes (Figura 10), usando los valores de entropía condicional promediados previamente en las celdas de 25m x 25m, para construir los mapas de entropía de la Figura 9.

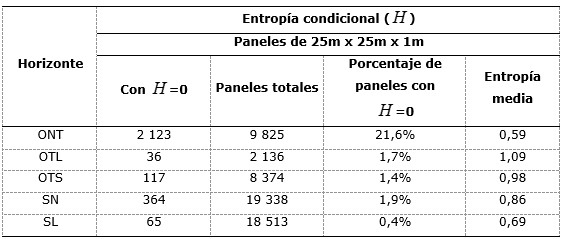
Se presenta también de forma tabulada la estadística global de la entropía condicional por horizontes de la corteza de meteorización según el modelo 3D de paneles de 25m x 25m x 1m (Tabla 3), donde se resume la cantidad de paneles con entropía igual a cero (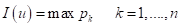=0) y la entropía media en cada horizonte.

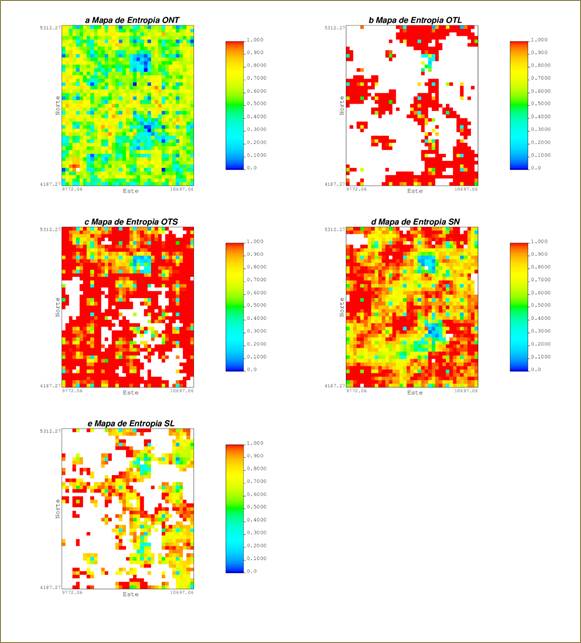
Figura 9 Mapas de entropía condicional de los horizontes de la corteza de meteorización, regularizados sobre el plano horizontal (2D), en celdas 25m x 25m. 

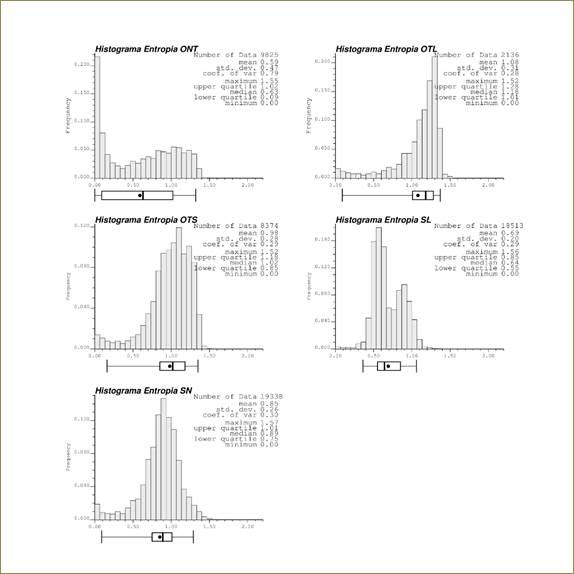
Figura 10 Histogramas de frecuencia y estadígrafos de entropía condicional 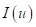en celdas 25m x 25m x 1m de los horizontes de la corteza de meteorización. 

Tabla 3 Estadística de la entropía condicional por horizontes de la corteza de meteorización según el modelo 3D de paneles de 25m x 25m x 1m 

DISCUSIÓN

Las curvas de proporcionalidad (Figura 2) obtenidas a partir de las proporciones calculadas en la Tabla 2, evidencian una relación directa de la profundidad con los horizontes de la corteza de meteorización, denotando la existencia de zonalidad en su distribución espacial según esa dirección, siendo más patente en el horizonte de los ONT en los cuales alcanza valores entre 0.50 a 0.99, así como también en las SN y SL de la parte media y baja del perfil de meteorización, con valores que van desde 0.5 a 0.75. Para los OTL y OTS la proporcionalidad calculada es inferior a 0.5. Todo lo anterior evidencia la no existencia de estacionariedad en la dirección vertical, lo que justifica el método empleado en la presente investigación para la modelación de los horizontes de la corteza de meteorización.

El estudio variográfico evidenció la existencia de isotropía en el plano de los horizontes de la corteza meteorización (Figura 3), dado que se observan alcances similares al variar la dirección acimutal, con alcances máximos que van desde los 45 m para las SN, hasta los 250 m para los OTL, ajustándose a las curvas experimentales a un modelo compuesto por dos estructuras esféricas con diferente alcance. En la primera estructura los alcances van de 30m-35m que excepcionalmente alcanzan los 70m (SL). En la dirección vertical se observan los menores alcances (de 4m a 11m), significando una rápida transición entre los horizontes de la corteza de meteorización en esa dirección, en ocasiones con incrementos por encima de la meseta de los semi-variogramas, lo cual es indicativo de no estacionariedad.

La comparación de los semi-variogramas indicadores simulados para 50 escenarios equiprobables horizontales (Figura 6, a-e) y verticales (Figura 6, f-j), contra los modelos teóricos ajustados, evidencia que se logran reproducir satisfactoriamente los alcances teóricos y las mesetas de los semi-variogramas indicadores simulados, tanto horizontales como verticales.

Al comparar los horizontes simulados según la red de nodos de 5m x 5m x 1m (escenario medio) con los mismos horizontes presentes en los compósitos usados como información condicionante al proceso de simulación, se evidencia que existe correspondencia (Figura 4). Se logra reproducir satisfactoriamente las proporciones medias originales de los horizontes de la corteza de meteorización para los ONT, OTL y OTS, no tanto así para las SN y SL cuyas proporciones quedaron algo subvaloradas para las primeras y sobrevaloradas para las segundas, probablemente relacionado al hecho de que la información condicionante de la parte inferior de la corteza de meteorización resulta insuficiente para reproducirlas satisfactoriamente (Figura 5).

En los modelos 3D de los horizontes de la corteza de meteorización y de la entropía condicional asociada en paneles de 25m x 5m x 1m (Figuras 7 y 8) como resultado del proceso de escalamiento de los 50 escenarios simulados puntualmente en red de 5m x 5m x 1m, se mantienen las proporciones de los horizontes, a pesar del cambio de escala (de puntual a volumétrica o panel) con respecto a la información condicionante (compósitos). El modelo de la entropía condicional evidencia que sus menores valores (con valor cero y próximos a este valor) se asocian con los paneles cercanos a los compósitos de las redes de 25m x 5m x 1m, 100m x 100m x 1m y la zona de perfiles dispuesto de forma radial a 12,5 m. Fuera de estas zonas la entropía se incrementa sustancialmente debido al insuficiente nivel de información, indicando un aumento de la incertidumbre para los horizontes de la corteza de meteorización. A juzgar por los mapas de entropía de la Figura 9 y los valores medios de las entropías condicionales por horizontes de la Tabla 3, el horizonte de los ONT resultó ser el de más baja entropía y mayor continuidad espacial (Figura 9 a), diferenciándose de los OTL y la SL, con menor continuidad (Figura 9 b y e).

Los histogramas de frecuencias (Figura 10) muestran un comportamiento multimodal, exhibiendo claramente la existencia de dos poblaciones con valores de entropías (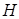) bien diferenciados; las frecuencias de bajos valores próximas a cero y la de altos valores, siendo las frecuencias de estas últimas más elevadas, con mayor esbeltez, excepto para el horizonte de los ONT donde las frecuencias de bajos valores sobrepasa a las de los altos valores, contrariamente al horizonte de las SN donde predominan las frecuencias de altos valores de .

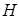De acuerdo con los valores de entropía de la Tabla 3, el horizonte de los ONT posee el mayor porcentaje de paneles con H=0, presentándose como el horizonte con baja entropía, lo que significa que su clasificación como panel correspondiente al horizonte de los ONT posee menos incertidumbre, dado que el grado de mezcla con los nodos de otros horizontes de la corteza de meteorización dentro de un mismo panel clasificado como tal (de acuerdo con su valor de probabilidad estimado), resulta bajo o nulo (21,6 %); con un valor bajo de entropía media de 0,59. Sin embargo, para los paneles clasificados como OTL, OTS, SN y SL, estos se presentan con pocos paneles con valor de entropía igual a cero; solo entre el 0,4 % y 1,9 % del total de paneles de estos horizontes poseen ese valor de entropía, exhibiendo los más altos valores de entropía media (entre 0,69 a 1,09). Consecuentemente presentan un mayor grado de incertidumbre, debido al alto grado de mezcla de nodos de diferentes horizontes dentro de un mismo panel como consecuencia del proceso de escalado a paneles de 25m x25m x1m.

CONCLUSIONES

• La estructura típica de los depósitos de corteza de meteorización y en particular del depósito de níquel San Felipe, argumenta la aplicación del empleo del algoritmo Simulación Secuencial Indicador con Proporciones Localmente Variables para modelar y cuantificar la incertidumbre de los horizontes de la corteza de meteorización.

• El nivel de información que posee el depósito de níquel San Felipe, dado el grado de estudio actual (los sectores más perspectivos están explorados fundamentalmente en una red de 100m x 100m), resulta aún insuficiente para reproducir con certidumbre el modelo de los horizontes de la corteza de meteorización, a juzgar por los valores de entropía resultantes de su simulación en paneles de 25m x 25m x 1m, en particular para los horizontes de las ocres texturales saprolíticos (OTS) y las serpentinitas nontronizadas (SN), dado que en ellos se concentra el mayor potencial de la mineralización niquelífera de interés industrial.

Agradecimientos

Los autores desean agradecer a Commercial Caribbean Nickel S.A., concesionaria del depósito de Níquel de San Felipe por permitir el uso de la información del área caso de estudio. A la Oficina Nacional de Recursos Minerales por el apoyo ofrecido, especialmente a la MSc. Yenibey Pérez Carrasco, directora técnica de la institución

REFERENCIAS

Babak, O.; Manchuk, J. G. and Deutsch, C. V. 2013: Accounting for non-exclusivity in sequential indicator simulation of categorical variables. Computers & Geosciences 51. ISSN 0098-3004. DOI 10.1016/j.cageo.2012.07.003. Disponible en: https://www.sciencedirect.com/science/article/pii/S0098300412002282.

Chang-Rodríguez, A. y Rojas-Purón, A. L. 2018: Movilidad geoquímica y grado de meteorización del yacimiento San Felipe, Camagüey, Cuba. Minería y Geología 34(2). Consulta: 28/02/2024. Disponible en: Disponible en: https://www.redalyc.org/journal/2235/223554994001/html/ .

Cobas-Botey, R. M. 2017: Modelo geológico descriptivo de las lateritas ferroniquelíferas del depósito San Felipe, Camagüey, Cuba. Tesis doctoral. Universidad de Moa Dr. Antonio Núñez Jiménez. Moa, Holguín.

Cobas-Botey, R. M.; Formell-Cortina, F. y Leyva-Rodríguez, C. A. 2017: Modelo geológico descriptivo del yacimiento laterítico San Felipe, Camagüey, Cuba. Minería y Geología 33(3). Consulta: 28/02/2024. Disponible en: Disponible en: https://www.redalyc.org/journal/2235/223551846001/html/.

Cowan, J.; Beatson, R.; Ross, H. J.; Fright, W. R.; Mclennan, T. J.; Evans, T. R.; Carr, J. C.; Lane, R. G.; Bright, D. V.; Gillman, A. J.; Oshust, P. A. y Titley, M. 2003: Practical implicit geological modelling. Fifth International Mining Geology Conference.

Dagasan, Y.; Erten, O.; Renard, P.; Straubhaar, J. and Topal, E. 2019: Multiple-point statistical simulation of the ore boundaries for a lateritic bauxite deposit. Stochastic Environmental Research and Risk Assessment 33(3). ISSN 1436-3259. DOI 10.1007/s00477-019-01660-8.

Deutsch, C. V. 2006: A sequential indicator simulation program for categorical variables with point and block data: BlockSIS. Computers & Geosciences 32(10). ISSN 0098-3004. DOI 10.1016/j.cageo.2006.03.005. Consulta: 28/02/2024. Disponible en: Disponible en: https://www.sciencedirect.com/science/article/pii/S0098300406000598 .

Echeverri-Londoño, A. 2016: Validación de modelos numéricos en geociencias a partir de simulaciones geoestadísticas con énfasis en simulaciones multipunto. Consulta: 28/02/2024. Disponible en: Disponible en: https://repositorio.uchile.cl/handle/2250/139151 .

Elias, M.; Stewart, L.; O’callaghan, P.; Martínez, A. and Smith, G. 2018: Ambatovy Nickel Project,Madagascar. NI-43-101 Technical Report. S.l.: CSA Global Mining Industry Consultants. R501.2018. Consulta: 28/02/2024. Disponible en: Disponible en: https://minedocs.com/20/Sherritt_International_Corp_Ambatovy_Nickel_Project_TR_06302018.pdf.

Gallardo, T.; Chang, A.; Tauler, E. y Proenza, J. 2010: El yacimiento de San Felipe (Camagüey, Cuba): un ejemplo de lateritas niquelíferas tipo arcilla. Macla, 13.

GEMCOM SOFTWARE INTERNATIONAL INC. 1998: Gemcom for Windows User Manual, Modelling. Volume III. Consulta: 28/02/2024. Disponible en: Disponible en: http://www.3ds.com/GEOVIA .

Goovaerts, P. 1997: Geostatistics for Natural Resources Evaluation. Oxford University Press. Applied geostatistics series, vol. 31. Disponible en: https://doi.org/10.1023/A:1007530422454.

Gray, G.; Sulway, R.; Cameron, A. y Stone, R. 2022: Ravensthorpe Nickel Operations NI 43-101 Technical Report. Western Australia. Consulta: 28/02/2024. Disponible en: Disponible en: https://s24.q4cdn.com/821689673/files/doc_downloads/2022/Ravensthorpe-NI-43-101-Technical-Report.pdf .

Hansen, T. 2020: Entropy and Information Content of Geostatistical Models. Mathematical Geosciences, 53. DOI 10.1007/s11004-020-09876-z.

Horton, J. and Lipton, I. 2002: Report on Estimation of Resources for the San Felipe Nickel Laterite Project for San Felipe Mining Ltd. In: International Mining Consultants Pty Ltd. IMC0923. Australia.

Hughes, F. y Cameron, C. 2012: Technical Report of Halleys, Hale-Bopp and Shoemaker-Levy Deposits, Ravensthorpe, Western Australia. Technical Report. Australia: First Quantum Minerals Ltd. Consulta: 28/02/2024. Disponible en: Disponible en: https://minedocs.com/20/Ravensthorpe-TR-2012.pdf .

Ilyas, A. y Koike, K. 2012: Geostatistical Modeling of Ore Grade Distribution from Geomorphic Characterization in a Laterite Nickel Deposit. Natural Resources Research, 21. DOI 10.1007/s11053-012-9170-8.

Jia, Q.; Li, W. y Che, D. 2020: A triangulated irregular network constrained ordinary Kriging method for three-dimensional modeling of faulted geological surfaces. IEEE Access, 8.

Journel, A. G. y Deutsch, C. V. 1993: Entropy and spatial disorder. Mathematical Geology, 25(3). ISSN 1573-8868. DOI 10.1007/BF00901422.

Kenworthy, A. 2015: Can implicit methods be used to model complex geology? Seequent. Consulta: 22/03/2024. Disponible en: Disponible en: https://www.seequent.com/can-implicit-methods-be-used-to-model-complex-geology/ .

Larrondo, P. 2003: Entropy of Gaussian Random Functions and Consequences in Geostatistics. CCG Annual Reports, Report 5. Consulta: 22/03/2024. Disponible en: Disponible en: https://ccg-server.engineering.ualberta.ca/CCG%20Publications/CCG%20Annual%20Reports/Report%205%20-%202003/83-Entropy.pdf .

Mizuno, T. A. y Deutsch, C. V. 2022: Sequential Indicator Simulation (SIS). Geostatistics Lessons. Consulta: 04/03/2024. Disponible en: Disponible en: https://geostatisticslessons.com/lessons/sequentialindicatorsim .

Richmond, A. 2013: Conditional Simulation of a Nickel Laterite Deposit using Unfolding. APCOM 2013: 6. Consulta: 16/02/2024. Disponible en: Disponible en: https://martlet.com.au/wp-content/uploads/2020/08/2013_APCOM_Richmond_Conditional_Simulation_of_nickel_laterite_deposit_using_unfolding.pdf .

Rodríguez-Catalá, A. y Rodríguez-Infante, A. 2021: Sistema de fallas del yacimiento laterítico niquelífero San Felipe, Camagüey, Cuba. Minería y Geología 37(2). ISSN 1993-8012. Consulta: 28/02/2024. Disponible en: Disponible en: http://scielo.sld.cu/scielo.php?script=sci_abstract&pid=S1993-80122021000200162&lng=es&nrm=iso&tlng=es .

Shannon, C. E. 1948: A mathematical theory of communication. The Bell System Technical Journal, 27(3). ISSN 0005-8580. DOI 10.1002/j.1538-7305.1948.tb01338.x.

Wellmann, J. F. y Regenauer-Lieb, K. 2012: Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models. Tectonophysics 526. Consulta: 29/02/2024. Disponible en: Disponible en: https://www.sciencedirect.com/science/article/pii/S0040195111001788 .

Xue, Y.; Sun, M. and Ma, A. 2004: On the reconstruction of three-dimensional complex geological objects using Delaunay triangulation. Geocomputation 20(7). ISSN 0167-739X. DOI 10.1016/j.future.2003.11.012. Consulta: 25/001/2024. Disponible en: Disponible en: https://www.sciencedirect.com/science/article/pii/S0167739X03002462

Recibido: 05 de Febrero de 2024; Aprobado: 21 de Marzo de 2024

^*Autor para la correspondencia: [e-mail]

Los autores declaran que no existen conflictos de intereses.

JAAT: conceptualización y procesamiento geoestadístico, redactor principal del trabajo original, revisión y aprobación de la versión final.

ACP: supervisor, diseño de la investigación, redacción final.

EEC: supervisor, diseño de la investigación; revisor del procesamiento y corredactor de la información geoestadística y de las figuras, gráficos y tablas.

RMCB: corredactora de parte geológica del depósito San Felipe, revisión de la terminología empleada.