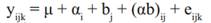Biomathematics

Application of the linear mixed and generalized mixed model as alternatives for analysis in experiments with repeated measures

Sarai Gómez^{1  *}  , Verena Torres¹  , Yolaine Medina¹  , Yusleiby Rodríguez¹  , Y. Sardiñas¹  , Magaly Herrera¹  , R. Rodríguez¹ 

¹Instituto de Ciencia Animal, Apartado Postal 24, San José de las Lajas, Mayabeque, Cuba

Abstract

Linear mixed and generalized linear mixed models were applied to an experiment with scarified seeds through the process of endozoochory, as tools for processing and analysis with measures repeated over time. Variables analyzed were plant height and stem thickness. Pearson correlation matrix was calculated to determine the existence of association among sampling days. In the analyzed variables, sphericity criterion was used by Bartlett statistic. For both variables, the assumption of normality was verified by Shapiro- Wilk and Kolmogorov-Smirnov tests. In the variable that fulfilled the assumption of normality, a linear mixed model was used. For the variable that was not fulfilled, the generalized linear mixed model was applied. The Poisson, Gamma, Log Normal, Normal and Binomial variants were analyzed to determine data distribution. Several variance-covariance structures were tested to select the best fit and the information criteria that obtained the smallest values were considered. The use of these statistical models allows to adequately control the probability of occurrence of type I error, since it provides greater flexibility and information when selecting the best fit model, in addition to allowing to analyze unbalanced data.

Key words: longitudinal data; covariance structures; information criteria

Introduction

One of the most used research methods is to measure the response variable in the same experimental unit at different moments in time. These are more efficient than using a different experimental unit for each measurement, since they require fewer units, which reduces sample size, minimizes costs, improves test power, and estimates over time is more accurate (^{Kuehl 2000}).

In the agricultural branch, experiments with these characteristics are often carried out. In these studies, it is not appropriate to use the classical linear models of analysis of variance (ANAVA), because when performing repeated measurements over time in the same experimental units, these are correlated. Therefore, it is not met with the traditional assumptions of independence and normality that are required for its use (^{Jerez et al. 2011})

Given the specific characteristics of these experiments with repeated measures, it is necessary to determine which analytical strategy is the most appropriate. Some authors have recently used linear mixed models and generalized linear mixed models, implemented in some statistical programs because of the advantages they have over traditional ones (^{Balzarini and Machiavelli 2005} and ^{Vallejo et al. 2010}).

The objective of this study was the application of the linear mixed model and the generalized linear mixed model, as a tool for processing and analyzing an experiment, with repeated measures to compare different varieties of trees subjected to the endozoochory process.

Materials and Methods

Experimental procedure. The study was developed in the ranch "El Peregrino", belonging to the Campus of the Faculty of Veterinary Medicine of the University of Colima, Mexico. In all cases, basic seed was used, except in moringa, from which seeds of trees belonging to the agricultural campus of the university were collected. Eight treatments were tested, which were Leucaena endozoochory (Leucaena leucocephala), coral endozoochory (Caesealpinia platyloba), scarified leucaena and Coral with water at 80 ºC (^{Toral and González 1999}), leucaena without scarification, coral without scarification, gliricidia without scarification, and moringa without scarification (Moringa oleifera).

Endozoochory process was developed with 12 Brahaman breed calves, with mean weights of 225 kg and 18 months of age, housed in independent pens, which received a silage base diet of CT-115, as well as 1 kg of supplement of waste banana.

Each animal was supplied with 1,000 seeds of each tree, mixed in the supplement. The total intake of seeds was determined by offer-rejection. Total collection of feces was carried out during 96 h at intervals of 24 h. Seeds collected from feces were dried at room temperature and placed in polyethylene bags. From the fifth day of collection, sowing was carried out under nursery conditions under a 50 % shade screen. The variables plant height and stem thickness (cm) were measured at 14, 21 and 28 d.

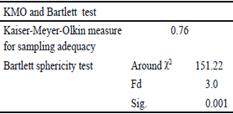
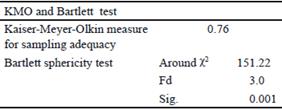
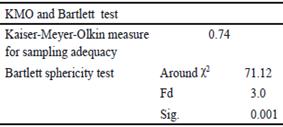
Statistical analysis. For the analyzed variables, Pearson correlation matrix was calculated, with the purpose of determining the existence of association between the sampling days. Sphericity criterion was used by ^{Bartlett (1937)} statistics and the measure of sample adequacy of Kaiser-Meyer-Olkin (KMO) (^{Pérez and Medrano 2010} and ^{Acosta et al. 2015}).

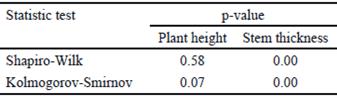
For both variables, the fulfillment of the assumption of normality was verified by the tests of ^{Shapiro and Wilk (1965)} and Kolmogorov -Smirnov modified by ^{Lilliefors (1967)}. To determine the distribution that followed the data, Proc Severity was used and the following were analyzed with their corresponding functions Poisson (Logarithmic), Gamma (Reciprocal), Log Normal (Log), Normal (Identity) and Binomial (Logit). In both variables, the plant was used as the experimental unit. Treatments and sampling days were considered as fixed effects. The interaction of both effects and the error were the random effects, respectively. For the estimation of the model, the Laplace method was used, which is adequate for the analysis of designs with measures repeated over time.

The general expression of the model for both cases is:

Where:

Yijk	variable expected respo nse of the study
µ	mean common to all observations
ai	fixed effect of the i-th treatment (i=1, …, 8)
bj	random effect of the j-th time (j= 14,21 and 28)
(ab)ij	fixed effect of the i-th treatment in interaction with the random effect of the j-th time (ij=1, …, 24)
eijk	random error associated to all observations

For the variable that did not fulfill the normality assumption, the generalized linear mixed model was used, which coincides with the model previously described, where Y_ijk= f(µ), response variable, according to the specific bond function μ= mean or intercept.

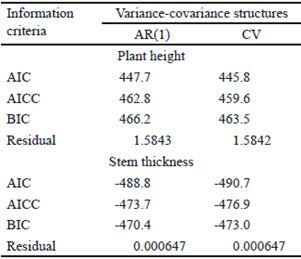
Several variance-covariance structures were examined. The Unstructured (UN), Toepliz (toep), Autoregressive of Order 1 (Ar (1)), Composite Symmetry (CS) and Components of Variance (CV) were used for obtaining the best fit. To make this selection, the Akaike (AIC), Akaike corrected (AICC) and Bayesian (BIC) information criteria were used, which would show the least value. Parameters were estimated by the methods of maximum likelihood (ML) or restricted maximum likelihood (REML) (^{Gualdrón 2009} and ^{Vallejo et al. 2014}).

For the comparison of means, ^{Kramer (1956)} test was used for P <0.05. Data processing was carried out with the ^{SAS (2013)}statistical package, version 9.3.

Results and Discussion

Tables 1 and 2 show correlation coefficients for the sampling days in the variables plant height and stem thickness. In both, values are higher than 0.70, which evidences high correlation for each variable among sampling days. Therefore, the assumption of independence of errors was not fulfilled.

Tables 3 and 4 show the results of ^{Bartlett (1937}) sphericity test and the KMO measure (^{Kaiser 1960}, (¹⁹⁷⁴) for both variables. Bartlett sphericity presented significant value (P <0.001), so the null hypothesis that the variance-covariance matrix is an identity matrix is rejected. The measure of sample adequacy of KMO was 0.76 and 0.74 respectively, both between the values established as acceptable by the literature (^{Salinas et al. 2014}). This shows that the model used was adequate and the analysis could be continued.

Table 1 Correlation coefficients for 14, 21 and 28 d in plant height 

Table 2 Correlation coefficients for 14, 21 28 d in stem thickness variable 

Tabla 3 Sphericity test for plant height 

Table 4 Sphericity test for stem thickness 

Table 5 shows the results of normality test, carried out using Shapiro Wilk and Kolmogorov Smirnov tests. The residuals of plant height variable were near a normal distribution, and a linear mixed model could be used. This was not the case for the variable stem thickness, so it was analyzed by means of a Generalized Linear Mixed Model, and adjusted to a Gamma distribution with Log link function.

Table 5 Normality test for plant height and stem thickness variables 

Table 6 shows covariance structures and information criteria studied. For the variables plant height and stem thickness, from all the analyzed structures, only CV and Ar (1) showed better performance. In both cases, the CV was selected, with a value of 445.8 and -490.7, respectively. Selection was based on the information criterion and on the covariance structure that showed the lowest value, since the model was better fitted.

Table 6 Covariance structures and information criteria for plant height 

Table 7 shows the results of the analysis of variance according to the Linear Mixed Model, in which the interaction days x treatment significantly influenced (P <0.001) on the variable plant height. For moringa without scarification, there was greater plant height at 28 d, without deferring from the measurement at 14 and 21 d. The lowest was obtained with gliricidia without scarification, at 14 d, which did not differ from that obtained at 21 d, but at 28 d.

Table 7 Means of treatment per day interaction for plant height 

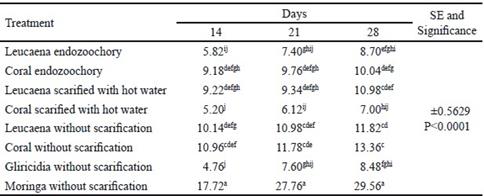
^a,b,c,d,eDifferent letters indicate significant differences for P<0.05

Table 8 shows the results of the analysis of variance according to the Generalized Linear Mixed Model for the variable stem thickness, where the interaction days x treatments was significant (P = 0.0031).

In the evaluation of stem thickness, moringa without scarification showed the highest values at 14, 21 and 28 d of sampling, although they did not show differences among them. Coral without scarification maintained a similar performance, although sampling days did not differ among them. The lowest value was obtained with gliricidia in its two variants. In both, there were no differences among sampling days.

Table 8 Means of treatment per day interaction for stem thickness 

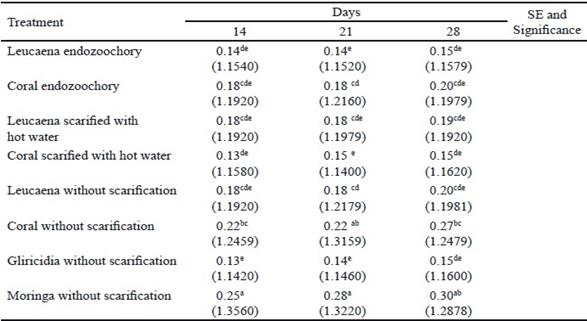
^a,b,c,d,e Different letters indicate significant differences for P<0.05. ( ) Estimated means for link function

When applying this procedure, the adequate use of statistical alternatives before the non-fulfillment of the assumptions of the analysis of variance was confirmed, specifically in the treatment of experiments with repeated measures.

Conclusions

Linear Mixed Models and Generalized Linear Mixed Models constitute an alternative of analysis before the non-fulfillment of the assumptions of the analysis of variance and before disadvantages that classic models presented in designs with repeated measures.

AIC, AICC and BIC information criteria allow the selection of the optimal structure of covariance, which permits a better fit of the model.

References

Acosta, A., Mónica, M. & Sánchez, JP.2015. Desempeño psicométrico de dos escalas de autoeficacia e intereses profesionales en una muestra de estudiantes de secundaria CES Psicología, 8(2): 156-170.

Balzarini, M. & Macchiavelli, R. 2005. Aplicaciones de Modelo Lineal Mixto en agricultura y forestería, Notas de Clase, Curso Internacional Aplicaciones de Modelo Lineal Mixto en Agricultura y Foresteria, p.189.

Bartlett, M. S. 1937. Properties of sufficiency and statistical tests. In: Proceedings of the Royal Statistical Society, Series A 160 (901): 268-282.

Gualdrón, J. C. 2009. Influencia de los criterios de selección AIC Y BIC para la selección del modelo de evolución y la reconstrucción del análisis bayesiano. http://tux.uis.edu.Co/labsist/docencia/finales/final2009-I/2050158-20070.pdf.

Jerez, M., Moret, A.Y., Carrero, O.E., Macchiavelli, R.E & Quevedo, A.M. 2011. Curvas de índice de sitio basadas en Modelo Lineal Mixto para plantaciones de teca (Tectona grandis L, F,) en los llanos de Venezuela, Agrociencia, 45 (1): 135-141.

Kaiser, H.F. 1974. An index of factorial simplicity. Psychometrika, 39 (1): 31-36.

Kaiser, Η. F. 1960. The application of electronic computers to factors analysis. Educational and Psychological Measurement, 40 (20): 141-151.

Kramer, C.Y. 1956. Extension of multiple range tests to group means with unequal numbers of replications. Biometrics, 12(3): 307-310.

Kuehl, R.O. 2000. Diseño de experimentos. Principios estadísticos de diseño y análisis de investigación. Ed. Universidad de Arizona. Arizona. USA. p. 6

Lilliefors, H. 1967. On the Kolmogorov-Smirnov test for normality with mean and variance unknown, Journal of the American Statistical Association, 62(318): 399-402.

Pérez, E.R. & Medrano, L.2010. Análisis Factorial Exploratorio: Bases Conceptuales y Metodológicas. Revista Argentina de Ciencias del Comportamiento, 2 (1): 58-66.

Salinas, JL., Espinosa, V., & González, HE. 2014. Características psicométricas de una escala de adherencia al tratamiento de diabetes mellitus II e hipertensión en una muestra de pacientes. Revista Electrónica de Psicología Iztacala, 17 (3): 905-929.

SAS. 2013. Sistema de análisis estadístico. Universidad de Nebraska. Versión 9.3.

Shapiro, S. & Wilk, B. 1965. An análisis of variante test for normality (complete simples) Biométrica, 52 (3): 591-611.

Toral, O & González, Y. 1999. Efecto del agua caliente en la germinación de diez especies arbóreas. Pastos y Forrajes, 22 (1): 47-53.

Vallejo, G., Arnau, J., Bono, R., Fernández, P, & Tuero, E. 2010. Selección de modelos anidados para datos longitudinales usando criterios de información y la estrategia de ajuste condicional, Psicothema, 22 (2): 323-333.

Vallejo, G., Arnau, J., Bono, R., Fernández, P. & Tuero, E. 2014. Selección de modelos anidados para datos longitudinales usando criterios de información y la estrategia de ajuste condicional. Psicothema , 22(2):323-333.

Received: December 18, 2017; Accepted: December 26, 2018

^*Email:[e-mail]