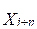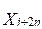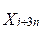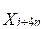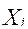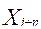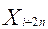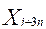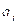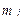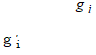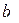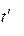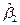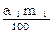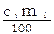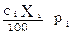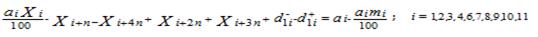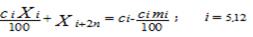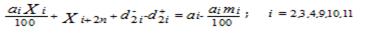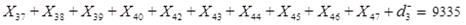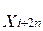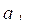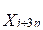Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
La producción y el crecimiento del rebaño del ganado vacuno se planifican con ayuda de cálculos especiales, en dependencia de las particularidades biológicas de cada una de las categorías de los animales (Prado, Fernández & Sagaró, 2007). No obstante, mediante la aplicación de los métodos convencionales de planificación no se logra una efectiva correlación de indicadores productivos, zootécnicos y económicos entre las distintas categorías de edad y sexo del ganado, lo que imposibilita seleccionar una adecuada estructura de la masa ganadera por categorías y un eficiente movimiento de rebaño.
La complejidad del proceso económico-productivo de la actividad ganadera dificulta considerablemente no sólo el análisis y comprensión de dicho objeto de estudio, sino también la integración de todos los factores condicionantes y la planificación de su desarrollo.
Una vía efectiva para lograr el perfeccionamiento de la planificación de los procesos económicos de la producción ganadera y su integración, es mediante la aplicación de técnicas de avanzada de gestión por medio de los métodos y modelos económico-matemáticos; por lo que constituye una necesidad en dichos procesos el empleo de técnicas modernas de gestión empresarial, adecuadas a cada escenario económico y productivo en particular.
Lo expresado da relevancia al problema científico abordado, que consiste en que la insuficiente integración de indicadores técnico-productivos y económicos limita la realización de un adecuado proceso de planificación de la producción ganadera.
Los trabajos sobre la utilización de los métodos cuantitativos en la planificación de la ganadería vacuna se encuentran dispersos y no son muy abundantes. Sin embargo, existen aplicaciones de modelos económico-matemáticos de programación lineal y de toma de decisiones multicriterios en la planificación de los procesos agropecuarios; entre otros se encuentran los realizados por González & Brezo (1987); Ahumada & Villalobos (2009); Mezghani, Rebai, Dammak & Loukil (2009); Stygar & Makulska (2010); Ortuño & Vitoriano (2011); Dave (2015); y Zgajnar & Kavcic (2016). Los trabajos desarrollados y aplicados de manera general han estado encaminados a la aplicación de métodos cuantitativos para la toma de decisiones en la planificación agropecuaria, en la optimización del balance alimentario, en la planificación del desarrollo perspectivo y optimización del movimiento de rebaño.
La literatura científica relacionada con la modelación matemática del movimiento de rebaño vacuno es exigua; no obstante, González & Brezo (1987), desarrollan un modelo matemático de programación lineal. Para su planteamiento matemático, establecen una acertada simbología para los diferentes elementos del movimiento de rebaño en sus diferentes fases, considerando por categoría de edad y sexo lo referente a: existencia al inicio y final de año, nacimientos, porcentaje de ganado extraído para carne o venta, porcentaje de pérdidas, peso promedio vivo de cada cabeza de ganado, transferencias a categorías superiores y llegadas de categorías inferiores.
El modelo de programación lineal desarrollado por González & Brezo (1987), presenta las siguientes limitaciones: no se encuentra debidamente estructurado, ya que no se definen las variables de decisión, ni los parámetros del modelo que permitan una construcción consecuente del sistema de restricción y de la función objetivo; no posee una metodología para determinar y validar los principales parámetros del modelo mediante la aplicación de las bondades que brinda el análisis econométrico y la estadística matemática; y el análisis económico realizado a la solución óptima es poco profundo, ya que no se hace un análisis integral de los resultados obtenidos correspondientes a variables, restricciones y función objetivo. No obstante, el modelo y el procedimiento propuesto por los autores de referencia, presentan un alto valor metodológico y científico.
El estudio realizado a los trabajos de Ahumada & Villalobos (2009); Mezghani, et al. (2009); Stygar & Makulska (2010); Ortuño & Vitoriano (2011); Dave (2015); y Zgajnar & Kavcic (2016), y de manera relevante el estudio efectuado al problema de optimización del balance de movimiento de rebaño planteado por González & Brezo (1987), permitió realizar el análisis propuesto, desarrollar y aplicar un modelo económico-matemático de meta con prioridad; técnica cuantitativa aplicada a los problemas de toma de decisiones multicriterios, fundamentada en los criterios dados por Moskowitz & Wright (1992); y Eppen, Gould, Schmidt, Moore & Watherford (2000), donde se exhibe una manera de resolver los problemas de programación lineal no factibles.
Los objetivos del trabajo consisten en diseñar un procedimiento para la programación del balance de movimiento de rebaño vacuno utilizando las técnicas cuantitativas de gestión, y demostrar la factibilidad del empleo del procedimiento propuesto como instrumento de planificación.
Con el cumplimiento de los objetivos planteados, se pretende, en haber contribuido al desarrollo del modelo de optimización del movimiento de rebaño, planteado por González & Brezo (1987).
Desarrollo
El desarrollo de la investigación se sustenta en la utilización de la metodología de la modelación económico-matemática, donde se utilizan, como base metodológica, los criterios planteados por Moskowitz & Wright (1992); y Eppen, et al. (2000).
El modelo que se expone fue aplicado en la planificación del movimiento de rebaño en una empresa de cría de ganado vacuno.
Formulación general del problema a modelar
La reproducción del rebaño se realiza de forma planificada mediante el balance del movimiento de rebaño, que constituye uno de los procesamientos de datos y tratamientos de la información más significativos del sistema de balance de planificación de la ganadería (González & Brezo, 1987).
En la producción ganadera aparecen condiciones alternativas para el movimiento de rebaño, que se reflejan en la siguiente problemática ¿Cuántas cabezas de cada categoría edad-sexo es necesario extraer y vender, así como transferir, a la categoría de orden superior?
La transferencia o extracción del ganado depende de la existencia de cabezas al inicio del año, de la cantidad de nacimientos, y de la necesidad de tener al final del año una determinada estructura en el rebaño, que garantice la reproducción normal del ganado en el futuro y el crecimiento de la producción de carne y leche según los ritmos planificados.
Además, es necesario tener en cuenta las siguientes situaciones: primero, el porcentaje de extracción de ganado para carne o para vender por cada categoría, deberá ser calculado de forma que se obtenga la cantidad máxima de producción ganadera y se asegure una correlación estructural entre categorías que permita la reproducción normal del rebaño en los siguientes ciclos de su desarrollo; segundo, las transferencias de los animales de una categoría a la superior, deben realizarse manteniendo los plazos de cría normales del rebaño en correspondencia con las características de cada categoría (González & Brezo, 1987).
Para lograr lo antes expuesto y dar solución a la problemática planteada, se utilizan los métodos modernos de planificación, mediante el empleo de técnicas cuantitativas de gestión como la modelación económico-matemática, que se ajusta a los requerimientos anteriores a través de un modelo de programación matemática de meta lineal con prioridades; modelo matemático más flexible que el de programación lineal, ya que permite que las metas conflictivas e inconmensurables sean especificadas y conduzcan a una solución satisfactoria en término de las metas prioritarias de la administración (Moskowitz & Wright, 1992).
Planteamiento matemático del modelo
Con el fin de lograr que el proceso económico modelado sea efectivo, se tienen en cuenta los factores más relevantes en la planificación del movimiento de rebaño, tratando de no soslayar aquellos que tienen mayor incidencia en la problemática, a fin de evitar decisiones erróneas. La posibilidad de conjugar estos factores sobre una base científicamente argumentada, se logra mediante la elaboración de modelos económico-matemáticos de programación de meta con prioridades para determinar la estructura satisfactoria del movimiento de rebaño.
Tomando como referencia a González & Brezo (1987), los elementos más relevantes del movimiento de rebaño del ganado vacuno pueden ser expresados mediante la nomenclatura de las variables de decisión y parámetros del modelo que se muestran en la tabla 1, donde el ganado vacuno se subdivide en una serie de categorías de edad-sexo, partiendo del desarrollo fisiológico de la masa ganadera y de las formas organizativas consideradas para su cría y explotación.
Tabla 1 Nomenclatura de las variables de decisión y parámetros del movimiento de rebaño
| Categorías de edad y sexo | Existencia al inicio del año (cabezas) | Nacimientos previstos cabezas) | Porcentaje de ganado extraído para carne o ventas |
Porcentaje de pérdidas (tasa de mortalidad) (%) | Peso vivo promedio de cada cabeza de ganado (kg) |
|---|---|---|---|---|---|
| 1- Vacas |
|
- | X1 | m1 | p1 |
| 2- Novillas |
|
- | X2 | m2 | p2 |
| 3- Añojas |
|
- | X3 | m3 | p3 |
| 4- Terneras, hasta un año |
|
- | X4 | m4 | p4 |
| 5- Terneras, crías |
|
c5 | X5 | m5 | p5 |
| 6- Toros para Ceba |
|
- | X6 | m6 | p6 |
| 7- Bueyes |
|
- | X7 | m7 | p7 |
| 8- Sementales |
|
- | X8 | m8 | p8 |
| 9- Toretes |
|
- | X9 | m9 | p9 |
| 10- Añojos |
|
- | X10 | m10 | p10 |
| 11- Terneros, hasta un año |
|
- | X11 | m11 | p11 |
| 12- Terneros, crías |
|
c12 | X12 | m12 | p12 |
| Total | - | - | - | - | |
| Categorías de edad y sexo | Llegadas de la categoría inmediata inferior  (cabezas) |
Transferencias de ganado a la categoría inmediata superior  (cabezas) |
Existencia al final del año  (cabezas) |
Compras a terceros  cabezas) |
|
| 1- Vacas | X13 | X25 = 0 | X37 | X49 | |
| 2- Novillas | X14 | X26 | X38 | X50 | |
| 3- Añojas | X15 | X27 | X39 | X51 | |
| 4- Terneras, hasta un año | X16 | X28 | X40 | X52 | |
| 5- Terneras, crías | X17 = 0 | X29 | X41 = 0 | X53 | |
| 6- Toros para Ceba | X18 | X30 = 0 | X42 | X54 | |
| 7- Bueyes | X19 | X31 = 0 | X43 | X55 | |
| 8- Sementales | X20 | X32 = 0 | X44 | X56 | |
| 9- Toretes | X21 | X33 | X45 | X57 | |
| 10- Añojos | X22 | X34 | X46 | X58 | |
| 11- Terneros, hasta un año | X23 | X35 | X47 | X59 | |
| 12- Terneros, crías | X24 = 0 | X36 | X48 = 0 | X60 | |
| Total | - | - | b | - | |
(Donde: i = 1,…,12 diferentes categorías de edad y sexo).
En la especificación de la nomenclatura, se anulan algunas variables de decisión y parámetros del modelo matemático de metas con prioridades, dado por las siguientes condiciones:
En las categorías superiores de vacas, toros, bueyes y sementales, no existen transferencias de animales a otras categorías superiores, por tanto, las variables transferencia de ganado a categorías superiores X25, X30, X31, y X32 son iguales a cero.
En las categorías inferiores de crías recién nacidas, no existe llegadas de otras categorías inferiores, pues no existen; en estas condiciones, las variables llegadas de categorías inferiores X17 y X24 se anulan.
Los animales pertenecientes a las categorías terneras y terneros crías al finalizar el año pasarán a la categoría superior terneras y terneros hasta un año de edad. En correspondencia con lo expresado, las variables existencia al final del año X41 y X48 son iguales a cero y, por consiguiente, las existencias a inicio de año de terneras y terneros crías son iguales a cero, por tanto los parámetros a5 y a12 se anulan.
Planteamiento matemático del modelo de meta con prioridades para la programación del movimiento de rebaño.
Índice:
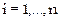Categorías de edad y sexo, con un valor de 
.
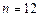donde: i = 1 Vacas; i = 2 Novillas; i = 3 Añojas; i = 4 Terneras, hasta un año; i = 5 Terneras, crías; i = 6 Toros para Ceba; i = 7 Bueyes; i = 8 Sementales; i = 9 Toretes;
i = 10 Añojos; i = 11 Terneros, hasta un año; e i = 12 Terneros, crías.
Las variables de decisión, se definen, como se exhibe en la tabla 2.
Tabla 2 Definición de las variables de decisión
| Notación | Definición de las variables de decisión |
|---|---|
|
Porcentaje de cabezas del rebaño destinadas a la venta o al sacrificio por categoría de edad y sexo i. |
|
Cantidad (número) de cabezas del rebaño correspondientes a la categoría de edad y sexo i, llegadas de la categoría inmediata inferior. |
|
Cantidad (número) de cabezas del rebaño correspondientes a la categoría de edad y sexo i, transferidas a la categoría inmediata superior. |
|
Cantidad (número) de cabezas del rebaño por categoría de edad y sexo i, al final del año (período de planificación). |
|
|
Cantidad (número) de cabezas de animales a comprar por categoría de edad y sexo i a terceros. |
Las variables de desviación, se definen, como se muestra en la tabla 3.
Tabla 3 Definición de las variables de desviación.
| Notación | Definición de las variables de desviación |
| d1i + y d1i - | Cantidad por encima y por debajo, respectivamente, respecto a la meta de la restricción del movimiento de las categorías por edad y sexo i del rebaño. |
| d2i + y d2i - | Cantidad por encima y por debajo, respectivamente, respecto a la meta de la restricción que garantiza la transferencia de animales hacia las categorías i inmediatas superiores. |
| d3 - | Cantidad por debajo respecto a la meta de la restricción que garantiza la existencia del rebaño planificado al final del año. |
| d4i + y d4i - | Cantidad por encima y por debajo, respectivamente, respecto a la meta de la restricción que garantiza la correlación estructural necesaria entre distintas categorías i. |
| d5 + y d5 - | Cantidad por encima y por debajo, respectivamente, respecto a la meta de la restricción que garantiza la producción mercantil de carne en pie del rebaño. |
Los parámetros y coeficientes del modelo, se definen, como se presentan en la tabla 4.
Tabla 4 Definición de los parámetros y coeficientes del modelo
| Notación | Definición de parámetros y coeficientes del modelo |
|---|---|
|
Número de cabezas del rebaño a inicio del año por categoría de edad y sexo i. |
| Número total de cabezas del rebaño a inicio del año. | |
|
|
Número de cabezas previstas a nacer de las categorías terneras crías y terneros crías i. |
|
Porcentaje de pérdida (tasa de mortalidad) por categoría de edad y sexo i. |
|
|
Kilogramos del peso vivo promedio de cada cabeza de ganado por categoría de edad y sexo i. |
|
Cantidad mínima y máxima de cabezas de ganados por categoría de edad y sexo i, respectivamente. |
|
|
Cantidad mínima y máxima de cabezas de ganados a comprar por categoría de edad y sexo i, respectivamente. |
|
Número de cabezas del rebaño planificadas total al final del año. |
|
|
Porcentaje mínimo y máximo de ganado extraído para carne o venta por categoría de edad y sexo i, respectivamente. |
|
Valor máximo de proporcionalidad de la correlación estructural entre la categoría de edad y sexo inferior (i+3n) con respecto a la categoría de edad y sexo inmediata superior [(i+3n)-1] del rebaño al final del año. |
|
|
Ritmo de crecimiento o decrecimiento del rebaño correspondiente a la ecuación de regresión estimada. |
| L superior | Límite superior del intervalo de confianza, para  . |
| B | Producción mercantil de carne en pie del rebaño. |
|
|
Número de cabezas del rebaño destinadas a la venta o al sacrificio por categoría de edad y sexo i, excepto terneras crías y teneros crías. |
|
Número de cabezas del rebaño que desaparezcan por las diferentes causas de pérdida, como mortalidad, por categoría de edad y sexo i, excepto terneras crías y teneros crías. |
|
|
Número de cabezas del rebaño destinadas a la venta o al sacrificio por categoría de edad y sexo de terneras crías y teneros crías. |
|
Número de cabezas del rebaño que desaparezcan por las diferentes causas de pérdida, como mortalidad, por categoría de edad y sexo de terneras crías y teneros crías. |
|
|
Término que representa la producción mercantil de carne en pie de las categorías de edad y sexo i, excepto las categorías terneras crías y terneros crías. |
|
Término que presenta la producción mercantil de carne en pie de las categorías de edad y sexo i, terneras crías y terneros crías. |
Definición de las metas de preferencia:
Se definen en orden de importancia decreciente, siendo P1 la prioridad más importante.
P1- Para garantizar producción mercantil de carne en pie del rebaño.
P2- Para garantizar el plan de cabezas del rebaño por categoría de edad y sexo al final del año.
P3- Para garantizar la adecuada correlación estructural entre distintas categorías.
P4- Para garantizar el adecuado movimiento de las categorías por edad y sexo del rebaño.
P5- Para garantizar la transferencia de animales hacia las categorías inmediatas superiores.
El sistema de restricciones del modelo económico-matemático de programación de meta con prioridades, se encuentra formado por el siguiente sistema de ecuaciones e inecuaciones.
La correspondencia existente entre los distintos elementos relevantes del movimiento de rebaño para cada una de las categorías por edad y sexo de los animales, se representa por la ecuación 1:
Ecuación 1. Restricción de tipo I que representa el movimiento de las categorías por edad y sexo del rebaño.
Las transferencias de todas las terneras y terneros crías a la categoría inmediata superior, excepto las crías que se destinan para el sacrificio y ventas, se puede expresar por la ecuación 2:
Ecuación 2. Restricción de tipo II que representa el movimiento de las categorías terneras crías y terneros crías del rebaño.
Las transferencias de categorías inferiores hacia categorías inmediatas superiores de todo el rebaño, excepto terneras y terneros crías, se puede formular por la ecuación 3:
Ecuación 3. Restricción de tipo III que garantiza la transferencia de animales hacia las categorías inmediatas superiores, excepto terneras y terneros crías.
Para garantizar un determinado rango en la cantidad de animales en algunas de las categorías, al finalizar del período de planificación, se consideran las siguientes inecuaciones 1 y 2:
Inecuación 1. Restricción de tipo IV que garantiza la cantidad mínima de animales al finalizar el período de planificación.
Inecuación 2. Restricción de tipo IV que garantiza la cantidad máxima de animales al finalizar el período de planificación.
Para garantizar la obtención de la cantidad total del rebaño planificado para el período, se considera la siguiente ecuación 4:
Ecuación 4. Restricción de tipo V que garantiza el rebaño planificado al final del período de planificación.
Para garantizar la correspondencia entre la transferencia de animales de una categoría a otra, se representan las siguientes ecuaciones 5 y 6:
Ecuación 5. Restricción de tipo VI que garantiza la transferencia de animales de una categoría a otra.
Ecuación 6. Restricción de tipo VI que garantiza la transferencia de toretes a las categorías superiores.
Para regular la extracción de animales para carne o venta dentro de cada una de las categorías, se platean las siguientes inecuaciones 3 y 4:
Inecuación 3. Restricción de tipo VII que garantiza la cantidad mínima de animales destinados para carne o venta.
Inecuación 4. Restricción de tipo VII que garantiza la cantidad máxima de animales destinados para carne o venta.
Para expresar las correlaciones estructurales entre las diferentes categorías de edad y sexo del rebaño, se considera la ecuación 7:
Ecuación 7. Restricción de tipo VIII que garantiza la correlación estructural necesaria entre distintas categorías.
Para garantizar la compra a terceros en el período de planificación, se plantean las siguientes inecuaciones 5 y 6:
Inecuación 5. Restricción de tipo IX que garantiza la cantidad mínima de animales a compras a terceros.
Inecuación 6. Restricción de tipo IX que garantiza la cantidad máxima de animales a compras a terceros.
Para garantizar el cumplimiento de la producción mercantil de carne en pie del rebaño, se formula la ecuación 8:
Ecuación 8. Restricción de tipo X que garantiza la producción mercantil de carne en pie del rebaño.
Por último, se consideran las restricciones de la condición de no negatividad de las variables de decisión y de las variables de desviación definidas en el modelo.
La función 1 objetivo del modelo matemático de meta lineal con prioridades, se construye considerando las variables desviación y el orden de prioridad establecido con los decisores, o sea:
Función 1. Minimización de las desviaciones entre las metas dentro de la estructura prioritaria asignada.
Esbozo teórico sobre la determinación y validación de la cantidad de cabezas del rebaño planificadas total al final del año (b)
La cantidad de cabezas del rebaño planificadas total al final del año se determina a partir de su comportamiento tendencial. Por tanto, inicialmente se estima el ritmo de crecimiento o decrecimiento de la masa ganadera (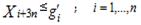) y a partir del mismo se determina cantidad de cabezas del rebaño planificadas para el final del período (b).
Para la estimación y validación del ritmo de crecimiento o decrecimiento del rebaño, se emplean las bondades de la estimativa y la inferencia del análisis regresión. Para determinar el modelo matemático de mejor ajuste, se tienen en cuenta la prueba de hipótesis F de Fisher, así como las diferentes pruebas de los supuestos básicos de autocorrelación, heterocedasticidad y normalidad. La estimación de los modelos de regresión lineal simple se apoya en la aplicación del paquete de programa estadístico y econométrico, Eviews. Los modelos de regresión lineal comprobados fueron el de tipo: lineal, cuadrático, y cúbico, entre los más importantes.
A partir del comportamiento anual de la cantidad total de animales del rebaño, es posible ajustar una función continua representada por la ecuación de regresión estimada 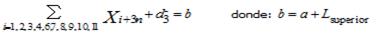donde, 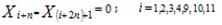es la cantidad de cabezas del rebaño al final del año, estimado por el modelo de regresión lineal en el período t (en cabezas); es la variable predictora tiempo (en año); 
y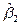 
estimadores mínimos cuadráticos, 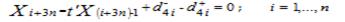, representa, el ritmo de crecimiento o decrecimiento del rebaño, en dependencia del signo, y es el intercepto.
Para determinar la precisión de la ecuación de regresión lineal estimada, se emplea la prueba de hipótesis F de Fisher, que se apoya en la descomposición de la variación total. Siendo el planteamiento de la prueba de hipótesis: Ho: (2 = 0; H1: (2 ( 0; donde: (2 representa el valor paramétrico correspondiente a la ecuación de regresión estimada.
Para comprobar la validez de las pruebas estadísticas de F de Fisher; así como la eficiencia de la estimación obtenida a partir de la ecuación de regresión, se procede a verificar los supuestos básicos del modelo mediante la comprobación de las pruebas: Durbin-Watson, General de Heterocedasticidad de White y Jarque-Bera.
Para hallar el comportamiento del ritmo de crecimiento o decrecimiento anual del rebaño, se toman como referencia los últimos quinces años, con el propósito de verificar las pruebas de hipótesis de referencia.
Análisis del intervalo de confianzas para el coeficiente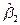 
de la ecuación de regresión
Para dar mayor flexibilidad al modelo de programación de meta lineal con prioridades, se realizan inferencias a partir de la estimación del intervalo de confianza al coeficiente de regresión, que expresa el ritmo de crecimiento o decrecimiento del rebaño al final del año, .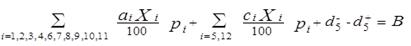
El intervalo de confianza es uno de los procedimientos generales de la inferencia estadística que puede aplicarse a los problemas de análisis de regresión, para realizar estimaciones y para el contraste de hipótesis. En el contexto de estimar el parámetro poblacional, el intervalo de confianza representado por 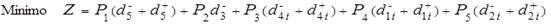es un rango de valores, calculado a partir de los datos de una muestra, en el cual podría encontrarse el verdadero valor del parámetro (Gujarati, 2003).
El término independiente b de la restricción cinco es el valor resultante de la suma algebraica de la existencia real inicial del rebaño (a) y el límite superior del intervalo de confianza de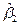
.
Resultados del análisis estadístico-matemático realizado al parámetro cantidad de cabezas del rebaño planificadas total al final del año (b)
El comportamiento del rebaño al final de año se ajusta a la ecuación de regresión predictora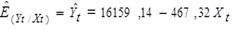 
, con coeficiente de correlación y de determinación de -0,937 y 0,878, respectivamente, como se exhibe en la tabla 5 del informe del EViews, lo que demuestra que la variable predictora explica que aproximadamente el 88% de la variación del movimiento de la existencia final de rebaño durante el período objeto de estudio. Por ende, se puede considerar el tiempo como una buena variable predictora, con el propósito de determinar el ritmo de crecimiento o decrecimiento de la masa ganadera anualmente.
Tabla 5 Resultado estadístico del modelo de regresión lineal (EViews).
| Dependent Variable: Y | ||||
|---|---|---|---|---|
| Method: Least Squares | ||||
| Included observations: 15 | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 16159.14 | 438.4172 | 36.85791 | 0.0000 |
| X | -467.3179 | 48.21947 | -9.691477 | 0.0000 |
| R-squared | 0.878419 | Mean dependent var | 12420.60 | |
| Adjusted R-squared | 0.869067 | S.D. dependent var | 2229.854 | |
| S.E. of regression | 806.8660 | Akaike info criterion | 16.34776 | |
| Sum squared resid | 8463425. | Schwarz criterion | 16.44216 | |
| Log likelihood | -120.6082 | F-statistic | 93.92473 | |
| Durbin-Watson stat | 1.508921 | Prob(F-statistic) | 0.000000 | |
Para verificar la confiabilidad de la ecuación de regresión ajustada y la validez de las proyecciones realizadas, se aplica la prueba de hipótesis de F de Fisher. Como la probabilidad de F-statistic o valor p igual a cero es menor que el nivel de significación del 0,05, por tanto la ecuación de regresión lineal simple se considera como buena predictora del valor del ritmo de decrecimiento de la masa ganadera partir de su comportamiento anual.
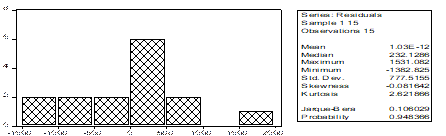
Para analizar la normalidad se toma como referencia la prueba Jarque-Bera (JB), cuyos resultados se muestran en la figura 1. Como la probabilidad asociada al estadístico JB de 0,94 es superior al nivel de significación del 0,05, no existen elementos para rechazar la hipótesis nula, lo que implica que la variable regresada rebaño al final del año sigue una distribución normal para un nivel de significación del 0,05. Como la asimetría toma valor negativo, la distribución normal presenta una deformación hacia la izquierda, y al ser la curtosis menor que tres, la distribución es menos apuntada que la normal, denominada platicúrtica.
Aplicando la Prueba Durbin-Watson se verificó que el valor estimado d es 1,508, cumple la condición du < d < (4-du), o sea, 1,361 < 1,508 < 2,639, situándose en la zona de aceptación, por lo que se puede afirmar, que no existe autocorrelación serial de primer orden.
Una forma para detectar la heterocedasticidad lo constituye la prueba general de heterocedasticidad de White, tabla 6. Como el valor del estadístico n▪R2 de 0,54 no es superior al valor crítico de X²(0,95; 2) igual a 5,99, no se rechaza la hipótesis nula, concluyendo que no existe heterocedasticidad. Este resultado se puede corroborar, ya que la probabilidad asociada al estadístico de 0,76 es superior al nivel de significación del 0,05.
Tabla 6 Prueba general de heterocedasticidad de White (EViews).
| White Heteroskedasticity Test: | |||
|---|---|---|---|
| F-statistic | 0.225256 | Probability | 0.801612 |
| Obs*R-squared | 0.542763 | Probability | 0.762326 |
Como resultado de aplicar las pruebas: Durbin-Watson, White y Jarque-Bera, se comprueba que no existe autocorrelación; que existe homocedasticidad en la varianza del error, es decir, las perturbaciones son homoscedásticas, y que existe normalidad en los residuos para un nivel de significación del 0,05, se concluye que la ecuación de regresión estimada constituye el modelo matemático adecuado que permite realizar las proyecciones correctas de la cantidad de cabezas del rebaño.
Determinada la ecuación de regresión lineal estimada y considerada como de buen ajuste y buena predictora, esta se utilizará para proyectar el comportamiento de la masa ganadera al final del período de un año, es decir, permitirá obtener el término independiente de la restricción de tipo cinco: rebaño planificado al final del período.
Con el interés de incorporarle mayor flexibilidad al modelo de programación de meta lineal para el movimiento del rebaño, se considera la necesidad de realizar inferencias a partir de la estimación del intervalo de confianza al coeficiente de regresión que expresa el ritmo de decrecimiento del rebaño al final del año.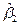
Los resultados del intervalo de confianza se obtienen mediante la utilización del paquete estadístico EViews, como se muestra en la tabla 7:
Tabla 7 Intervalos de confianza para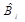 
(EViews).
| Coefficient Confidence Intervals | |||
|---|---|---|---|
| Variable | Coefficient | 95% CI | |
| Low | High | ||
| C | 16159.14 | 15212.000 | 17106.286 |
| X | -467.31 | -571.490 | -363.146 |
En correspondencia con lo expresado en la restricción representada por la ecuación 4, esta se acota con el valor resultante de adicionar a la existencia real inicial el límite superior del intervalo de confianza, resultando como el término independiente de la restricción la cantidad de 9335 animales, es decir, 9698 menos 363,146, generándose la restricción particular (ecuación 9).
Ecuación 9. Restricción de tipo V que garantiza el rebaño planificado al final del período de planificación en caso analizado.
Análisis de la solución obtenida
Para el análisis de la solución del modelo, se toma como referencia el reporte del Programa WinQSB correspondiente al módulo Linear goal programming and Integer linear goal programming. Los resultados de la solución satisfactoria han sido tabulados en la tabla 8, lo que constituye una adecuada presentación del balance de movimiento de rebaño por categorías.
Tabla 8 Movimiento de rebaño propuesto para el año 2017.
| Categorías de edad y sexo | Rebaño al inicio del año | Entradas | |||||
|---|---|---|---|---|---|---|---|
| Animales |
Estructura (%) | Nacimientos |
Llegadas de la categoría inmediata inferior |
Compras a terceros |
|||
| Vacas | 3463 | 35,71 | - | 1983 | 0 | ||
| Novillas | 2280 | 23,51 | - | 366 | 0 | ||
| Añojas | 557 | 5,74 | - | 721 | 0 | ||
| Terneras, hasta un año | 1140 | 11,76 | - | 896 | 0 | ||
| Terneras, crías | 0 | 0,00 | 943 | 0 | 0 | ||
| Toros para Ceba | 308 | 3,18 | - | 260 | 0 | ||
| Bueyes | 195 | 2,01 | - | 76 | 0 | ||
| Sementales | 2 | 0,02 | - | 0 | 0 | ||
| Toretes | 259 | 2,67 | - | 559 | 0 | ||
| Añojos | 356 | 3,67 | - | 785 | 0 | ||
| Terneros | 1138 | 11,73 | - | 979 | 0 | ||
| Terneros, crías | 0 | 0,00 | 1030 | 0 | 0 | ||
| Total |
|
100 | 1973 | 6625 | 0 | ||
| Categorías de edad y sexo | Salidas | ||||||
Transferencias de ganado a la categoría inmediata superior (X25 a X36) (cabezas) |
Ventas a otras empresas o para el sacrificio | Pérdidas o(cabezas) |
|||||
Porcentaje de ganado extraído (X1 a X12) (%) |
Animales o (cabezas) |
Peso vivo promedio (kg) | Total extraído para carne (kg) | ||||
| Vacas | 0 | 8 | 277 | 360 | 99720 | 90 | |
| Novillas | 1983 | 11 | 251 | 240 | 60240 | 46 | |
| Añojas | 366 | 25 | 139 | 220 | 30580 | 52 | |
| Terneras | 721 | 28 | 319 | 120 | 38280 | 100 | |
| Terneras, crías | 896 | 0 | 0 | 0 | 0 | 47 | |
| Toros para Ceba | 0 | 20 | 62 | 420 | 26040 | 5 | |
| Bueyes | 0 | 8 | 16 | 400 | 6400 | 5 | |
| Sementales | 0 | 0 | 0 | 450 | 0 | 0 | |
| Toretes | 336 | 85 | 220 | 320 | 70400 | 12 | |
| Añojos | 559 | 35 | 125 | 220 | 27500 | 58 | |
| Terneros | 785 | 20 | 228 | 120 | 27360 | 125 | |
| Terneros, crías | 979 | 0 | 0 | 0 | 0 | 51 | |
| Total | 6625 | - | 1636 | - | 386520 | 591 | |
| Categorías de edad y sexo | Variable de desviación restricción movimiento de rebaño 
|
Término independiente de la restricción | Rebaño al final de año | ||||
Animales (cabezas) (X37 a X48) |
Estructura (%) | ||||||
| Vacas | 1299 | 0 | 3373 | 3850 | 41,24 | ||
| Novillas | 0 | 1434 | 2234 | 1800 | 19,28 | ||
| Añojas | 71 | 0 | 505 | 650 | 6,96 | ||
| Terneras | 0 | 37 | 1040 | 933 | 9,99 | ||
| Terneras, crías | 0 | 0 | 896 | 0 | 0,00 | ||
| Toros para Ceba | 201 | 0 | 303 | 300 | 3,21 | ||
| Bueyes | 0 | 0 | 190 | 250 | 2,67 | ||
| Sementales | 0 | 0 | 2 | 2 | 0,02 | ||
| Toretes | 0 | 0 | 247 | 250 | 2,67 | ||
| Añojos | 0 | 0 | 298 | 400 | 4,28 | ||
| Terneros | 79 | 0 | 1013 | 900 | 9,64 | ||
| Terneros, crías | 0 | 0 | 979 | 0 | 0,00 | ||
| Total | - | - | - |
|
100,00 | ||
Análisis de las entradas del balance de movimiento de rebaño
Un momento trascendental en el movimiento de rebaño son los cambios de categorías que se originan en correspondencia con la edad y sexo del rebaño, es decir las transferencias que se producen de la categoría inferior a la categoría inmediata superior dentro del mismo sexo. En total se produce el traslado natural entre las categorías de 6625 animales, y tienen un peso importante las transferencias de las categorías de edades inferiores a las categorías vacas, añojas, terneras, añojos y terneros, representando el 80,96% de las transferencias totales.
Análisis de las salidas del balance de movimiento de rebaño
El porcentaje satisfactorio del rebaño extraído para la venta o el sacrificio con respecto a la existencia inicial, se encuentra formado por nueve categorías por grupos de edad y sexo, como se muestra a continuación: 8% de las vacas, 11% de las novillas, 25% de las añojas, 28% de las terneras, 20% de los toros, 8% de los bueyes, 85% de los toretes, 35% de los añojos, y 20% de los terneros. En total se extraen para la venta o el sacrificio 1636 cabezas.
La cantidad satisfactoria de cabezas del rebaño destinados a la venta o sacrificio desglosado por categoría de edad y sexo permitirá alcanzar una producción mercantil de carne en pie del rebaño total anual de 386520 kg, superior en 37985 kg, es decir, en un 10,90% a la producción mercantil planificada de carne en pie del rebaño total.
Los terneros, las terneras hasta un año, las vacas y los añojos son las categorías que mayor incidencia tienen en las pérdidas por muerte, constituyendo el 63,11% del total de las muertes.
Análisis de la estructura satisfactoria del rebaño completo al final de año
Para el análisis del balance de movimiento de rebaño desde la perspectiva productiva y económica, es indispensable la evaluación de la estructura más adecuada del rebaño al final de año, siendo la solución satisfactoria la mejor variante en el contexto del modelo matemático planteado; es decir, es la estructura que mejor representa las existencias finales por cada una de las categorías, la cual queda representada por la cantidad de animales y el porcentaje exhibido en las dos últimas columnas de la tabla 8, alcanzando un rebaño total de 9335 cabezas.
Se destaca que las vacas y novillas, como categorías estratégicas para el desarrollo de la masa ganadera, representan el 60,52% del rebaño al final de año, lo que contribuirá a garantizar para el año 2017 la reproducción y futuro crecimiento del rebaño, así como, lograr el nivel satisfactorio de producción de leche planificada anual de 750000 litros.
Comparación entre la estructura propuesta y la planificada por la empresa
La comparación entre la estructura del rebaño derivada de la solución satisfactoria del modelo matemático de meta con prioridades y la estructura del rebaño planificada por la empresa para el año, es un aspecto importante en el análisis de la solución satisfactoria obtenida, y que sirve para medir la validez de la proyección realizada, máxime cuando se estudia el comportamiento y evolución de la masa ganadera que constituye un proceso económico-productivo complejo.
Al contrastar la estructura propuesta del rebaño al final de año con respecto a la estructura planificada por la empresa para el mismo período, se plantea un crecimiento del 1,46% de cabezas con respecto a lo planificado, equivalente a 134 animales como se exhibe en la tabla 9.
Tabla 9 Estructura propuesta y planificada del rebaño para final de año.
| Categorías de edad y sexo | Estructura propuesta del rebaño al final de año | Estructura planificada del rebaño por la empresa | Diferencia de la propuesta respecto al plan | ||
|---|---|---|---|---|---|
| Animales (cabezas) | Estructura (%) | Animales (cabezas) | Estructura (%) | Cabezas | |
| Vacas | 3850 | 41,24 | 3728 | 40,52 | 122 |
| Novillas | 1800 | 19,28 | 1840 | 20,00 | -40 |
| Añojas | 650 | 6,96 | 571 | 6,20 | 79 |
| Terneras | 933 | 9,99 | 856 | 9,30 | 77 |
| Toros para Ceba | 300 | 3,21 | 198 | 2,15 | 102 |
| Bueyes | 250 | 2,67 | 182 | 2,00 | 68 |
| Sementales | 2 | 0,02 | 2 | 0,02 | 0 |
| Toretes | 250 | 2,67 | 148 | 1,61 | 102 |
| Añojos | 400 | 4,28 | 782 | 8,50 | -382 |
| Terneros | 900 | 9,64 | 894 | 9,70 | 6 |
| Total | 9335 | 100 | 9201 | 100 | 134 |
Para comprobar si existe correspondencia entre la estructura satisfactoria, obtenida a partir de la solución del modelo de meta y la estructura planificada, se aplica la prueba estadística de Rango de Wilcoxon, prueba no paramétrica para dos muestras relacionadas. Como el valor p obtenido de la prueba 0,153 es mayor que un nivel de significación del 0,05, no se rechaza la hipótesis nula, por tanto se puede afirmar que la estructura satisfactoria propuesta del rebaño para final del año y la estructura planificada del rebaño para final de año, no difieren, no existiendo diferencias estadísticamente significativas entre ambas estructuras. No obstante, la estructura satisfactoria propuesta presenta mejores características, con respecto a la composición de las categorías relevantes del rebaño que definen su desarrollo perspectivo.
Análisis de la estructura propuesta del rebaño hembra para final de año
Dada la situación existente a inicio de año es necesario realizar determinados cambios que permitan alcanzar un rebaño hembra al final del horizonte de planificación, con valores próximos a las proporciones de la estructura deseada. La empresa para garantizar la estructura propuesta de la solución satisfactoria del modelo en el rebaño de hembra al final del año, próxima a la estructura deseada, debe prever un incremento de las vacas y añojas, así como una disminución de las novillas, con respecto a la estructura real a inicio de año, tabla 10. La estructura propuesta del rebaño hembra se acerca más a la deseada, que la estructura real existente a inicio de año, lo que posibilita una mejor composición de vacas, novillas y añojas.
Tabla 10 Estructura propuesta del rebaño hembra al final de año y real al inicio de año.
| Categorías de edad y sexo | Estructura propuesta del rebaño hembra al final de año | Estructura real del rebaño hembra al inicio de año | Diferencia de la propuesta respecto al real (cabezas) | Estructura deseada | ||
|---|---|---|---|---|---|---|
| Animales (X37 a X40) (cabezas) | Estructura (%) | Animales (cabezas) | Estructura (%) | Estructura (%) | ||
| Vacas | 3850 | 53,22 | 3463 | 46,54 | 387 | 50,00 |
| Novillas | 1800 | 24,88 | 2280 | 30,64 | -480 | 20,00 |
| Añojas | 650 | 9,98 | 557 | 7,50 | 93 | 10,00 |
| Terneras | 933 | 12,89 | 1140 | 15,22 | -207 | 20,00 |
| Total | 7233 | 100 | 7440 | 100 | -207 | 100,00 |
Conclusiones
La aplicación de la programación de meta lineal con prioridades evidencia las posibilidades de su utilización en la planificación de los procesos económicos en la ganadería, pues flexibiliza y amplía las posibilidades del análisis de la solución.
La metodología propuesta proporciona los procedimientos necesarios para determinar y validar parámetros del modelo, mediante la aplicación del análisis estadístico matemático.
La estructura satisfactoria del movimiento de rebaño, muestra un crecimiento de la producción ganadera con respecto al plan previsto y una adecuada estructuración del rebaño hembra, debido a una mejor estrategia del movimiento de rebaño en sus diferentes fases.
La solución del modelo matemático permite una reestructuración más eficiente de la composición por categoría de edad y sexo, en función de la mayor producción mercantil de carne en pie del rebaño, lográndose beneficios productivos, al aumentar la producción mercantil total de carne con respecto al obtenido por los métodos convencionales de planificación.
