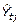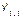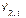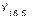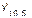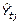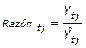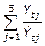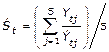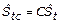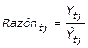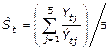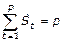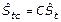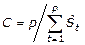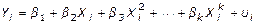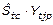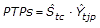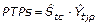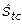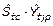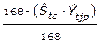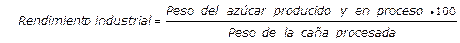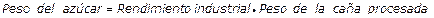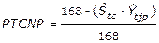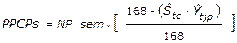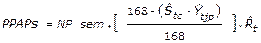Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Según Freitas, et al. (2019), las empresas no pueden ser competitivas sin una planificación eficiente de sus procesos productivos; resaltan que para lograr la competitividad y eficiencia deseada las empresas invierten capital en la reducción de sus tiempos empleados, pues esto traería para ellas una disminución en los costos de operación. Por esa razón, consideran que la gerencia del tiempo constituye uno de los factores de mayor pertinencia en la administración de la producción, y su reducción como una ventaja competitiva importante.
En correspondencia con lo señalado, un elemento importante relacionado con la planificación de la agroindustria azucarera es la disminución del tiempo perdido. En el contexto de este escenario se desarrolla el presente trabajo, que aborda la planificación vista desde la perspectiva del pronóstico del tiempo perdido como instrumentos de planificación e integrador del proceso de producción.
El tiempo perdido en la industria azucarera, Morales (1993), lo define como la cantidad de horas y minutos que están detenidos, por cualquier razón, los tándems o molinos de la industria azucarera, o sea, es el tiempo que han estado sin procesar caña los tándems que componen el equipo de molienda de la industria, cualesquiera que sean las causas industriales o no industriales que lo originó (Estrada, 1987). Existe una estrecha relación entre el tiempo perdido y el aprovechamiento de la capacidad industrial instalada, por tal motivo su pronóstico juega un papel importante en la proyección del plan de caña a procesar y del volumen de producción de azúcar.
En el trabajo solo se presenta el estudio del tiempo perdido total, resultante del tiempo perdido debido a causas industriales y no industriales.
El proceso de producción de la industria azucarera cubana tiene lugar durante determinados meses del año, una de las tareas más importantes es la decisión de su delimitación en el tiempo, es decir, durante cuántos meses y a partir de qué momento debe desarrollarse la molienda. La delimitación de la zafra, fecha de inicio y estimado del final, se hacen en función de la disponibilidad de la caña en el campo, del comportamiento histórico del tiempo perdido en la producción azucarera, y de las características climatológicas, siempre buscando que a dicho período le corresponda el mayor rendimiento industrial.
El tiempo perdido es un indicador que, en el corto plazo, tiene importancia para establecer la eficiencia de la gestión industrial, y su estudio contribuye a tomar decisiones para el mejor desempeño de las campañas futuras. Lograr una disminución del tiempo perdido debe generar una mayor dinámica en la producción de azúcar y un menor estancamiento en la zafra.
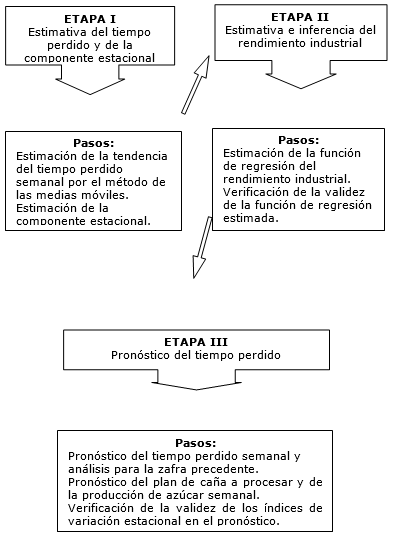
El procedimiento propuesto para el pronóstico del tiempo perdido en la industria azucarera consta de las siguientes etapas: estimativa del tiempo perdido y de la componente estacional, estimativa e inferencia del rendimiento industrial, y pronóstico del tiempo perdido. En esta última etapa se realiza el pronóstico del plan caña a procesar semanalmente y el pronóstico del plan de producción de azúcar semanal para la zafra próxima.
Desarrollo
Morales (1993), plantea que hasta ese momento no se ha podido establecer un método cuantitativo que permita la fundamentación científica para la planificación del tiempo perdido; no obstante, e independientemente que los procesos agroindustriales azucareros son sistemas complejos por la incidencia directa de los fenómenos naturales, y en correspondencia con Fernández, et al. (2019), es factible la representación de estos sistemas complejos a través de Modelos Estadísticos Matemáticos, donde estos modelos permiten su descripción, realizar análisis cuantitativos detallados, predecir el comportamiento de los objetos en diversas condiciones y desarrollar técnicas que permiten establecer estrategias de trabajo para lograr soluciones satisfactorias.
Se ha constatado que no existen evidencias de investigaciones recientes sobre el pronóstico del tiempo perdido en la industria azucarera, sin embargo, se cuentan con los antecedentes siguientes: una Metódica del pronóstico del tiempo perdido industrial en un Complejo Agroindustrial azucarero elaborada por Pérez (1986), y de una propuesta general para la proyección del tiempo perdido realizada por Morales (1993), en su libro Programación y economía de la zafra.
La Metódica del pronóstico del tiempo perdido exhibida por Pérez (1986), se descompone en los siguientes pasos generales: se estiman las ecuaciones de tendencia del tiempo perdido total y por rubros, apoyándose en el método de los mínimos cuadrados ordinarios, se aplica el método de alisamiento exponencial sobre la base de la información obtenida del paso anterior y, por último, se realiza el pronóstico del tiempo perdido.
La propuesta presentada por Morales (1993), cuando realiza el análisis del aprovechamiento de la capacidad industrial, exhibe una síntesis sobre la proyección del tiempo perdido, donde dada la complejidad de la variable a pronosticar, y la influencia que sobre ella ejercen los factores climatológicos, plantea hacer tres proyecciones para el tiempo perdido: optimista, promedio y pesimista, en dependencia de la causa tiempo perdido por lluvia, y propone un método que articula con el trabajo desarrollado por Pérez (1986).
Del estudio realizado a las investigaciones precedentes sobre el pronóstico del tiempo perdido planteado por Pérez (1986); y Morales (1993), le permitió a Infante (2019), perfeccionar los conocimientos generales y diseñar una Metodología para el pronóstico y análisis del efecto económico del tiempo perdido en la industria azucarera.
En concordancia con Hanke & Reitsch (2010), todos los procedimientos formales de pronóstico comprenden la extensión de las experiencias del pasado al futuro incierto. Aceptar que las técnicas de pronósticos funcionan sobre datos generados en sucesos históricos pasados conduce a que, metodológicamente, el pronóstico se apoye en una serie de pasos que deben seguirse para resolver el problema objeto de estudio. En tal sentido, plantean que se pueden identificar cuatro momentos en el proceso de pronóstico: recopilación de datos, reducción o condensación de datos, construcción del modelo, y extrapolación del modelo, o sea, el pronóstico.
Teniendo como base metodológica los estudios precedentes, el procedimiento propuesto para el pronóstico del tiempo perdido en la industria azucarera consta de las etapas y pasos siguientes:
Una vez profundizado en los conocimientos teóricos y prácticos de las investigaciones vinculadas al proceso de pronóstico en la industria azucarera, se pretende probar que, si se dispone de un procedimiento para el pronóstico del tiempo perdido sobre bases científicamente fundamentadas, se dispondrá de los medios que permiten la integración de indicadores productivos que posibilitan un adecuado proceso de planificación de la zafra.
El procedimiento propuesto y los resultados obtenidos se articulan con el proceso de planificación empresarial, permitiendo la proyección e integración de los indicadores relevantes de producción y de eficiencia de la programación de zafra, teniendo como sustento científico el pronóstico del tiempo perdido y sus índices de variación estacional.
Estimación de la tendencia del tiempo perdido semanal por el método de las medias móviles
Según Hooda, et al. (2020), los pronósticos pueden ser obtenidos usando métodos y técnicas estadísticas diversas como la regresión, las series temporales, y los modelos estocásticos; cada metodología tiene sus propias ventajas y limitaciones. El modelar series temporales surge para el análisis cuando las variables tienen de forma natural un orden secuencial con el paso del tiempo.
La relevancia de la aplicación de los métodos estadísticos para Makridakis, et al. (2020), radica en su coherencia y en la posibilidad de manipular grandes series temporales como un todo integrado, en contraste con los métodos convencionales donde se utiliza el juicio como única opción para realizar estimaciones para el futuro.
La información cuantitativa correspondiente al indicador tiempo perdido en la producción azucarera, se caracteriza porque los datos de la serie no exhiben un comportamiento regular y uniforme en el tiempo; debido a la irregularidad de ese comportamiento, no pueden ajustarse a un patrón específico, que pudiera ser representado por una función matemática. Además, su conducta no depende de otros factores que sean fácilmente cuantificables, para ser representados por variables cuantitativas.
En la literatura, para mejorar la eficiencia y la exactitud del pronóstico de los datos de la serie de tiempo, se tienen en cuenta una gran variedad de métodos y modelos de pronóstico (Mehmood, et al., 2019). Por su parte Angelo, et al. (2017), plantean que, entre los métodos de predicción para las series temporales, se cuenta con la media móvil, la descomposición clásica, el alisamiento exponencial, Box Jenkins, redes neuronales, etc.
Debido a las características que presenta el tiempo perdido y el interés de la investigación de obtener la componente estacional, se utiliza como método de estimación las medias móviles. De acuerdo con Espallarga & Solís (2012), la aplicación del método de estimación de los mínimos cuadrados y el pronóstico del análisis de regresión no garantizan una adecuada extrapolación de la tendencia o pronóstico de la serie; sin embargo, el método de las medias móviles proporciona para este caso resultados más satisfactorios, ya que junto con la tendencia, recoge una porción del efecto de los movimientos cíclicos presentes en la serie, lo que permite una estimación más depurada de la estacionalidad.
Como se expresó, para describir el comportamiento del tiempo perdido a través del tiempo, se estima su tendencia mediante el método de las medias móviles, que consiste en suavizar la serie mediante el cálculo de sucesivas medias correspondientes a subperíodos determinados.
A partir de la tabla 1, se expone el procedimiento utilizado para el cálculo de la estimación de la tendencia del tiempo perdido por el método de las medias móviles.
Tabla 1 - Tiempo perdido estimado por el método de las medias móviles.
| Período | Tiempo perdido de la semana t en la zafra j  (en horas) |
Total móvil | Promedio móvil | Tiempo perdido de la semana t en la zafra j estimado por el método de las medias móviles (Promedio móvil centrado)  (en horas) |
|||
| Zafra | Mes | ||||||
| Serie alargada | 20 |
|
- | - | - | ||
| 21 |
|
- | - | - | |||
| Primera zafra (j = 1) | Dic | 1 | 1 |
|
- | - |
|
| 2 | 2 |
|
- | - |
|
||
| - | - |
|
|
- | |||
| 3 | 3 |
|
- | - |
 |
||
| - | - |
|
|
- | |||
| 4 | 4 |
|
- | - |
 |
||
| - | - |
|
|
- | |||
| Ene | 1 | 5 |
|
- | - | - | |
| 2 | 6 |
|
- | - | - | ||
| 3 | 7 |
|
- | - | - | ||
| 4 | 8 |
|
- | - | - | ||
| . . . | . . . | . . . | . . . | . . . | . . . | ||
| Mayo | 1 | 21 |
|
||||
| Zafras 2 a la 4 | - | … | . . . | . . . | . . . | . . . | |
| Quinta Zafra (j = 5) | Dic | 1 | 1 |
|
- | - | - |
| 2 | 2 |
|
- | - | - | ||
| 3 | 3 |
|
- | - | - | ||
| 4 | 4 |
|
- | - | - | ||
| . . . | . . . | . . . | . . . | . . . | . . . | ||
| Abril | 1 | 17 |
|
- | - | - | |
| - | - |
|
|
- | |||
| 2 | 18 |
|
- | - |
 |
||
| - | - |
|
|
||||
| 3 | 19 |
|
- | - |
 |
||
| - | - |
|
|
- | |||
| 4 | 20 |
|
- | - |
|
||
| Mayo | 1 | 21 |
|
- | - |
|
|
| Serie alargada | 1 | - |
|
- | - | - | |
| 2 | - |
|
- | - | - | ||
Donde: t son las semanas, con t = 1,..., 21, y j son las zafras, con j = 1,…, 5.
Primero: Se toma la información semanal correspondiente al tiempo perdido en horas de las últimas cinco zafras precedentes, de tal manera que cada fila se corresponda con el tiempo perdido semanal de las cinco zafras analizadas. Para el caso que se ilustra, suponer que las zafras tienen fechas de inicio en el mes de diciembre y de terminación en el mes de mayo.
Segundo: Para estimar la tendencia del tiempo perdido semanal, por el método de las medias móviles, se procede como sigue:
Teniendo en cuenta el carácter cíclico de producción azucarera, que no completa el período de un año y que se organiza en semanas durante cuatro o cinco meses al año, se consideran los promedios móviles de cuatro semanas.
Como el promedio móvil a utilizar es par, hay que centrar los datos, inicialmente se calculan los promedios móviles sucesivos correspondiente a subperíodos de cuatro semanas (ejemplo: P 3 y P 4), a partir de estos promedios móviles, se calcula el promedio móvil centrado correspondiente a dos promedios móviles sucesivos, (para el ejemplo es
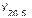). Este resultado, es el tiempo perdido de la semana t en la zafra j estimado por el método de las medias móviles (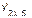), dichos tiempos estimados permiten suavizar a la serie original tiempo perdido de la semana t en la zafra j (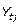). Para calcular el tiempo perdido estimado de las dos semanas situadas al inicio de la serie, o sea,
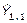y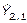 
, y de las dos últimas semanas de la serie, o sea, 
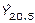y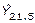 
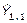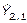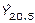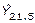, es necesario alargar la serie original, para poder ajustar dichas semanas al inicio y al final. Para calcular y , se estiman los valores correspondientes a Ysemana20 y Ysemana21 de la serie alargada y para calcular y , se estiman los valores correspondientes a Y
semana1 y Y
semana2 de la serie alargada.
Los cálculos desarrollados en esta tabla y en las siguientes es factible procesarlos en la hoja de cálculo del tabulador electrónico Microsoft Office Excel.
Desde el punto de práctico la tendencia del tiempo perdido, estimado por el método de las medias móviles, le imprime mayor flexibilidad al proceso de planificación, pues permite estimar el tiempo perdido para cada una de las semanas, lo que posibilita realizar una mejor programación de la zafra en función de la utilización de las capacidades industriales, diferente a como se realiza tradicionalmente, donde se planifica un tiempo perdido fijo para toda la zafra que limita la fundamentación técnica y económica de las decisiones a tomar.
Estimación de la componente estacional
El cálculo de la estimación de la componente estacional proporciona los índices de variación estacional semanales. De acuerdo con Pérez (1986), estos índices son valores adimensionales que reflejan las variaciones que se presentan semanalmente en el indicador tiempo perdido, sobre la base de datos históricos.
Existen varios métodos para calcular los índices de variación estacional, siendo los más utilizados, el de razón con la tendencia y el promedio móvil. Para calcular los índices de variación estacional semanales asociados al tiempo perdido se utiliza el método de razón con la tendencia, empleando el modelo multiplicativo.
Para el cálculo del índice de variación estacional semanal, se toma como referencia la tabla 2.
Tabla 2 - Índice de variación estacional semanal.
| Mes | Semana | Tiempo perdido de la semana t en la zafra j. Serie original  (en horas) |
Tiempo perdido de la semana t en la zafra j estimado por el método de las medias móviles (Promedio móvil centrado)  (en horas) |
Razón entre el tiempo perdido de la serie original y el estimado por el método de las medias móviles 
|
Suma semanal de la división del tiempo perdido de la serie original entre el estimado por el método de las medias móviles 
|
Índice de variación estacional semanal (Estimación de la componente estacional semanal) 
|
Índice de variación estacional corregido semanal (Estimación de la componente estacional corregida semanal) 
|
||||||||||||
| Zafra | Zafra | Zafra | |||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |||||
| Dic | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| . . . | … | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | . . . | . . . | . . . |
| Mayo | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
Primero: Para el cálculo de los índices de variación estacional semanales, inicialmente se calcula la razón entre el tiempo perdido de la serie original y el estimado por el método de las medias móviles, o sea, dicha razón es el cociente de dividir el valor tiempo perdido de la semana t en la zafra j de la serie original (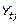) entre el valor de la tendencia del tiempo perdido de la semana t en la zafra j estimado por el método de las medias móviles, promedio móvil centrado (
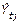), obteniéndose así, la razón entre ambos tiempos como se muestra en la ecuación 1. Para efectuar cada división los valores de los subíndices t, así como, los valores de los subíndices j de ambos tiempos, numéricamente deben ser iguales.
Ecuación 1. Razón entre el tiempo perdido de la serie original y el estimado.
Segundo: Se calcula el promedio de las razones entre los tiempos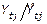 
, para cada semana t, como se muestra en la ecuación 2, dicho resultado, representa el índice de variación estacional semanal o la estimación de la componente estacional para cada semana.
Ecuación 2. Índice de variación estacional semanal.
Tercero: Para la estimación de la variación estacional, en el modelo multiplicativo, se establece la restricción planteada en la ecuación 3.
Ecuación 3. Restricción para la estimación de la variación estacional.
Donde p es la estación correspondiente, en semanas.
Cuarto: Si la restricción, representada por la ecuación 3, no se cumple, para cada semana será necesario determinar el índice de variación estacional semanal corregido o estimación de la componente estacional corregida semanal, a partir de la ecuación 4.
siendo 
Ecuación 4. Índice de variación estacional corregido semanal.
Donde C es el factor de corrección.
Para tener una mejor comprensión de los resultados obtenidos del índice de variación estacional semanal o de la estimación de la componente estacional, y poder valorar la utilidad de los resultados, a modo de ejemplo, se tiene que:
Si el tiempo perdido presenta un índice de variación estacional semanal por encima del 100%.
Se interpreta como un incremento promedio con respecto a la tendencia, del porcentaje dado, que esté por encima del 100% (Espallarga & Solís, 2012).
De forma práctica, si el tiempo perdido presenta un índice de variación semanal del 109% para la quinta semana, indica que en esta semana, hay un aumento promedio del tiempo perdido respecto a la tendencia de un 9%, lo que muestra la necesidad de tomar medidas técnico-productivas y organizativas que conduzcan a la reducción del tiempo perdido.
Si el tiempo perdido presenta un índice de variación estacional semanal por debajo del 100%.
Se interpreta como un decrecimiento promedio con respecto a la tendencia, del porcentaje dado, que esté por debajo del 100% (Espallarga & Solís, 2012).
De forma práctica, si el tiempo perdido presenta un índice de variación semanal del 90% para la décima semanal, indica que en esta semana, hay una disminución promedio del tiempo perdido respecto a la tendencia de un 10%. Esto permite planificar un procesamiento de caña superior para la semana.
Una aplicación importante de los índices de variación estacional semanal consiste en que, al multiplicar el índice de variación estacional semanal por el valor de un indicador productivo determinado de la industria azucarera, posibilitará representar el comportamiento del indicador durante la zafra, como se muestra en las aplicaciones desarrolladas en la etapa III.
La utilidad práctica los índices de variación estacional semanal del tiempo perdido es que permiten conocer las semanas donde históricamente se producen variaciones significativas, lo que posibilita una planificación más objetiva, y tomar las medidas y decisiones oportunas para su reducción.
Estimación de la función de regresión del rendimiento industrial
Existen múltiples factores que inciden en el comportamiento del rendimiento industrial, por lo que sería útil considerarlos para pronosticar el rendimiento industrial en función de estos, pero establecer esta relación presenta limitaciones que afectan la calidad del pronóstico, tales como: no todos los factores se pueden determinar cuantitativamente, no es posible obtener para la mayor parte de los factores un número alto de observaciones, existe interdependencia entre algunos factores, algunas de las variables explicatorias no están sujetas a control, etc.
Para Mehmood, et al. (2019), si los valores y datos pasados son conocidos y apropiados, se pueden utilizar posteriormente como la información necesaria para realizar pronósticos, mediante el empleo de diferentes métodos y modelos utilizados para ello. Si el propósito consiste en estudiar la dependencia entre variables, con la finalidad de predecir el valor medio de la variable dependiente en términos de los valores conocidos de las variables explicativas, y de acuerdo con Hooda, et al. (2020), el análisis de regresión representa la técnica estadística que frecuentemente se emplea para hacer tales investigaciones y modelar la relación entre variables.
En concordancia con Argüelles, et al. (2019), el análisis de regresión brinda una herramienta muy útil y potente para realizar el trabajo de modelación, y proporciona las técnicas estadísticas que tratan de explicar cómo se relaciona una variable respuesta con una o más variables predictoras. Aseveran que, lo que caracteriza en principio a las distintas clases de modelos de regresión es la naturaleza de la variable dependiente; si la variable es continua los modelos de regresión lineal son los más utilizados.
Por lo expuesto, mediante el análisis de regresión, utilizando el conjunto de variables explicativas expresadas por los factores de referencia, no posibilitarían realizar los cálculos pertinentes debido a las limitantes existentes. Al realizar un análisis de comportamiento del rendimiento industrial, se constata que este varía en función del tiempo de duración de la zafra en forma parabólica, como polinomios de segundo y tercer grados, en dependencia del grado de madurez y del contenido de sacarosa de la caña de azúcar.
El tiempo por sí solo no determina el rendimiento industrial, sin embargo, el rendimiento industrial sí se puede proyectar considerando el factor tiempo solamente, ya que la madurez y el contenido de sacarosa de la caña se modifican en función del tiempo. Factor de decisión importante que, para Junqueira & Morabito (2017), hay que tener en cuenta en la cosecha de la caña, para que no se comprometan los patrones de calidad en la producción de azúcar, pues incide en el máximo rendimiento azucarero de las variedades de caña plantadas.
Por lo expresado hasta aquí, el análisis estadístico matemático que se puede utilizar en el estudio del rendimiento industrial, de manera general, es la estimativa e inferencia del análisis de los modelos de regresión, donde se considera como única variable predictora el tiempo de duración de la zafra.
Los modelos de regresión polinomiales de grado k, en su forma general, representado por la ecuación 5, y de acuerdo con Gujarati & Porter (2010), son modelos donde existe una sola variable explicativa,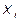
, en el miembro derecho de la función, la cual se encuentra elevada a distintas potencias, o sea, , 
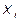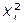, y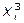 
; esto convierte a dichas funciones en modelos de regresión múltiples.
Ecuación 5. Forma general de los modelos de regresión polinomiales de grado k.
Por sus características la función del rendimiento industrial se ajusta a los modelos de regresión múltiples expresado en la ecuación 5, en concordancia con Gujarati & Porter (2010), son lineales con respecto a los parámetros, por consiguiente las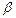
pueden ser estimadas mediante la aplicación de las metodologías usuales del método de los mínimos cuadrados ordinarios o máxima verosimilitud, sin que se presenten problemas especiales de estimación.
Los modelos lineales referidos constituyen el caso más conocido de modelos matemáticos, pero son sumamente útiles si el objetivo corresponde más al campo de la estimación y del pronóstico. Además, estos son muy utilizados por lo simple del método matemático que utilizan para estimar sus parámetros, método de los mínimos cuadrados ordinarios, el cual es exacto y la solución es única (Fernández, et al., 2019).
Por tanto, teniendo en cuenta el análisis realizado, se confirma que para estimar la función o ecuación de tendencia del rendimiento industrial, modelo matemático que describe cierto comportamiento del fenómeno a través del tiempo, se puede emplear la estimativa e inferencia de los modelos de regresión lineal múltiples.
A partir de la tabla 3, se expone el procedimiento de cálculo.
Tabla 3 - Rendimiento industrial estimado.
| Mes | Variable explicativa tiempo (en semana) |
Rendimiento industrial de la semana t en la zafra j |
Rendimiento industria promedio semanal de las zafras seleccionadas |
Rendimiento industrial estimado semanal obtenido del modelo de regresión que mejor ajusta |
||||
|---|---|---|---|---|---|---|---|---|
| Zafras | ||||||||
| 1 | 2 | 3 | 4 | 5 | ||||
| Dic | - | - | - | - | - | - | - | - |
| … | … | … | … | … | … | … | … | … |
| Mayo | - | - | - | - | - | - | - | - |
Se establece una tabla donde cada fila representa las semanas y las columnas el rendimiento industrial.
Inicialmente se toma la información semanal correspondiente al rendimiento industrial real de las cinco zafras precedentes, o sea, el rendimiento industrial de la semana t en la zafra j (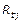
).
Para determinar el rendimiento industrial estimado semanal con respecto a su comportamiento histórico en función del tiempo, se calcula previamente rendimiento industrial promedio semanal, de las últimas cinco zafras (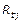), y se ajusta el comportamiento del promedio semanal mediante la aplicación del método de los mínimos cuadrados ordinarios, por medio de la aplicación del paquete de programa econométrico Eviews, o del paquete de programa estadístico SPSS, que posibilitan obtener los resultados estadísticos de los modelos matemáticos a estimar.
Por tanto, a partir del promedio rendimiento industrial semanal, es posible ajustar curvas continuas, como las que se representan en su forma general en la ecuación 6, por las funciones de rendimiento industrial estimado.
Ecuación 6. Funciones de regresión del rendimiento industrial estimado.
Donde,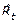 
es el rendimiento industrial estimado (en porcentaje),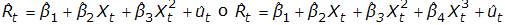es la variable explicativa tiempo (en semanas), 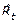son los coeficientes de regresión parcial estimados, con j = 2, 3, 4, y 
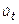es el término residual. Los signos de la función dependen del comportamiento de la serie de los datos u observaciones ajustadas.
Los modelos ajustados para examinar el rendimiento industrial son las funciones cuadráticas y cúbicas, las que exhiben coeficientes de determinación múltiple con valores superiores al 81% de la variabilidad total en rendimiento industrial explicada por el tiempo. Ese valor, para estos modelos lineales resume la proporción de la variabilidad en la variable dependiente, asociada con los factores de predicción de las variables independientes (Krauss, et al., 2018).
Verificación de la validez de la función de regresión estimada
Logrado el ajuste y estimada la función de regresión polinomial cuadrática o cúbica correspondiente al problema estudiado, se analiza la precisión de función, o sea, se verifica si la variable tiempo es capaz de explicar significativamente el comportamiento del rendimiento industrial; entonces, con el objetivo de determinar si la función estimada explica o no el problema objeto de estudio, se efectúa el análisis de varianza en la regresión, como medio esclarecedor y complementario para examinar el problema de la inferencia estadística.
A partir de los resultados del análisis de varianza, se realiza la prueba F de Fisher, donde la hipótesis nula que se somete a prueba expresa que la función estimada no es la adecuada y que no explica el problema objeto de estudio, versus la hipótesis alternativa a contrastar que plantea que la función estimada se puede considerar adecuada y que explica el problema en estudio.
Las pruebas F de Fisher referida, así como, la prueba t de Student proporcionan dos formas alternas, pero complementarias, de probar la hipótesis nula en los modelos con una variable explicativa. No obstante, en los modelos de regresión múltiple, la prueba F tiene varias aplicaciones que hacen que sea un método útil y poderoso para demostrar las hipótesis estadísticas (Gujarati & Porter, 2010).
Para verificar la validez de la prueba estadística F de Fisher en la significación de la función de regresión estimada, así como, la eficiencia de las predicciones obtenidas a partir de la función de regresión estimada, se procede a verificar los supuestos básicos del modelo, contrastando la veracidad de los supuestos de no autocorrelación, homocedasticidad y normalidad en los que se ha basado la construcción del modelo econométrico, o sea, para justificar la precisión de la función de regresión estimada del rendimiento industrial, se emplean las pruebas Durbin-Watson, Breusch-Godfrey, general de la heterocedasticidad de White y Jarque-Bera. De ser necesario, se realizan las correcciones necesarias y, de esta forma, se selecciona la mejor función de regresión que sirva de base para el pronóstico.
Si se comprueba que no existe autocorrelación, que existe homocedasticidad en las varianzas del error, es decir, son perturbaciones homocedásticas, y que existe normalidad para un nivel de significación seleccionado, se concluye que las funciones de regresión representadas por las funciones de segundo grado o de tercer grado constituyen los modelos matemáticos apropiados y permitirán realizar las proyecciones correctas y eficientes del rendimiento industrial.
Por tanto, seleccionar una u otra función de regresión polinomial estimada para el pronóstico del rendimiento industrial es válido. No obstante, es factible seleccionar la función de regresión polinomial cuadrática, por los resultados satisfactorios obtenidos en la verificación de las pruebas estadísticas, y porque, como ventaja adicional, posee una expresión más sencilla, lo que facilita los cálculos.
Utilidad práctica de los resultados obtenidos:
El modelo de pronóstico representado por la función de regresión lineal múltiple del rendimiento industrial le imprime mayor flexibilidad al proceso de planificación, pues permite proyectar el rendimiento industrial estimado para cada una de las semanas, posibilitando realizar una mejor programación de la zafra en función de la utilización de las capacidades industriales, en contraste a como se realiza de forma tradicional, donde se planifica un rendimiento industrial fijo para toda la zafra, lo cual limita la fundamentación científica de las decisiones a tomar.
En los casos estudiados, se comprobó la existencia de no autocorrelación, de perturbaciones homocedásticas y de normalidad para los modelos de regresión del rendimiento industrial. Esto corrobora la validez de la prueba estadística F de Fisher, así como la validez y eficiencia de los valores estimados del rendimiento industrial. Por tanto, los resultados satisfactorios obtenidos de aplicar las diferentes pruebas demuestran que los modelos de pronóstico seleccionados representan las funciones adecuada para pronosticar el rendimiento industrial.
Pronóstico del tiempo perdido semanal
Los índices de variación estacional semanales, obtenidos en la etapa uno, constituyen la herramienta científica que permite realizar las aplicaciones que se desarrollan a continuación.
Aplicación I: Análisis del pronóstico del tiempo perdido semanal para la zafra próxima y análisis para la zafra precedente
El análisis del pronóstico tiempo perdido se puede realizar para la zafra próxima, de manera que se conozca anticipadamente cuál debe ser su comportamiento. Además, el análisis del tiempo perdido se puede efectuar para la zafra precedente, con el propósito de comprobar si su comportamiento fue normal o determinar las irregularidades ocurridas.
En ambos análisis, se procede multiplicando los índices de variación estacional corregida semanal o estimación de la componente estacional corregida semanal (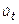), obtenidos en la etapa I, por el valor del tiempo perdido estimado promedio de la semana t (
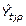), obtenido a partir del promedio móvil centrado, o por el valor del tiempo perdido promedio de la semana t (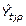), obtenido a partir de la serie original.
A continuación, se pormenoriza el cálculo del pronóstico del tiempo perdido semanal para la zafra próxima y del tiempo perdido semanal de la zafra precedente, tomando como referencia la tabla 4.
Tabla 4 - Pronóstico del tiempo perdido semanal.
| Mes | Semana | Tiempo perdido  (en horas) |
Tiempo perdido (en horas) |
Índice de variación estacional corregida semanal (Estimación de la componente estacional corregida semanal) 
|
Tiempo perdido semanal de la zafra precedente  (en horas) |
Pronóstico del tiempo perdido semanal para la zafra próxima ( (en horas) |
| Dic | - | - | - | - | - | - |
| . . . | . . . | - | - | - | - | - |
| Mayo | - | - | - | - | - | - |
Primero: Se calcula el tiempo perdido promedio de la semana t (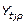), para las cinco zafras analizadas, como el valor promedio del tiempo perdido de la semana t en la zafra j de la serie original (
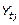). Se calcula el tiempo perdido estimado promedio de la semana t (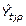), para las cinco zafras analizadas, como el valor promedio del tiempo perdido de la semana t en la zafra j, estimado por el método de las medias móviles (
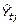). Para el cálculo de ambos promedios, se toman como referencia los valores de 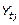y 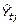, que se encuentran en las columnas 3 y 4, de la tabla 2, etapa I.
Segundo: A partir de los índices de variación estacional corregida semanal (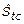), se determina el tiempo perdido semanal de la zafra precedente, mediante la multiplicación del índice de variación estacional corregida semanal (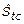) por el tiempo perdido promedio semanal (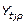), obtenido a partir de la serie original.
Tercero: A partir de los índices de variación estacional corregida semanal (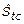), se determina el pronóstico del tiempo perdido semanal para la zafra próxima, ecuación 7, mediante la multiplicación del índice de variación estacional corregida semanal (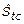) por el tiempo perdido estimado promedio semanal (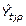), obtenido a partir del promedio móvil centrado.
Ecuación 7. Pronóstico del tiempo perdido semanal para la zafra próxima.
Cuarto: Con el propósito de verificar la validez del pronóstico del tiempo perdido semanal para la zafra próxima, se plantea la prueba estadística de rango de Wilcoxon, prueba no paramétrica para dos muestras relacionadas. La prueba propuesta permite comprobar si existe correspondencia del pronóstico del tiempo perdido semanal para la zafra próxima, (PTPs), y el tiempo perdido promedio semanal, obtenido a partir de la serie original ().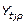
La hipótesis nula que se somete a prueba plantea que el pronóstico del tiempo perdido semanal para la zafra próxima (PTPs), y el tiempo perdido promedio semanal, obtenido a partir de la serie original (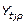), no difieren; por su parte, la hipótesis alternativa a contrastar expresa que difieren.
Como regla de decisión, si el valor de la probabilidad de la prueba estadística es mayor que el nivel de significación fijado, no se rechaza la hipótesis nula. Por tanto, se puede afirmar que, el pronóstico del tiempo perdido y el tiempo perdido promedio semanal, no difieren.
El estudio estadístico para realizar prueba de Wilcoxon se apoya en la aplicación del paquete de programa SPSS.
Utilidad práctica de los resultados obtenidos:
A partir de los índices de variación estacional semanal, se determina el pronóstico del tiempo perdido semanal para la zafra próxima, que permite a los decisores de la entidad azucarera realizar una planificación más objetiva y efectiva sobre bases científicamente fundamentadas, como se exhibe en la aplicación II.
A partir de los índices de variación estacional semanal, se determina el tiempo perdido semanal de la zafra precedente, que permite realizar un análisis retrospectivo acerca del comportamiento del tiempo perdido en dicha zafra y evaluar determinadas medidas para su ulterior reducción.
Mediante la aplicación de la prueba de hipótesis para dos muestras relacionadas de rangos de Wilcoxon, en los casos estudiados, se comprobó que entre las series correspondiente al pronóstico del tiempo perdido semanal para la zafra próxima y el tiempo perdido promedio semanal, no existen diferencias estadísticamente significativas.
Aplicación II: Pronóstico del plan de caña a procesar y de la producción de azúcar semanal para la zafra próxima
Conforme con Junqueira & Morabito (2018), la planificación de la zafra es un problema complejo y multifactorial, pues considera varios factores, tales como período de maduración de la materia prima, recolección, transportación, así como la capacidad de molida de la industria azucarera, siendo indispensable y fundamental la integración de estas etapas agrícola e industrial.
En el contexto anterior, la aplicación de los índices de variación estacional semanales, es altamente significativa, ya que permiten determinar el pronóstico y estimación del plan de caña a procesar semanalmente y del plan de azúcar a producir semanalmente. Resultados que posibilitan realizar la integración del plan de procesamiento de caña y de producción de azúcar semanal, considerando normas operacionales y rendimientos industriales diferentes para cada semana, de modo que el plan se ajuste mejor a la realidad e integre adecuadamente los indicadores relevantes de la programación de zafra.
Para realizar los pronósticos, se considera como indicador de partida en el pronóstico del tiempo perdido semanal (PTPs), calculado a partir del índice de variación estacional corregida semanal y del tiempo perdido estimado promedio semanal; así como, el tiempo de cumplimiento de la norma potencial, y la norma potencial; a partir de estos últimos, se obtiene el pronóstico del plan de caña a procesar semanal para la zafra que se planifica, que a su vez constituye el indicador principal para determinar el pronóstico del plan de azúcar a producir semanal.
A continuación, se muestra el cálculo del pronóstico del plan de caña a procesar semanal y del plan de producción de azúcar semanal; para lo cual se toma como referencia la tabla 5.
Tabla 5 - Pronóstico del plan de caña a procesar y del plan de azúcar a producir semanal.
| Mes | Semana | Tiempo perdido  (en horas) |
Índice de variación estacional corregida semanal 
|
Pronóstico del tiempo perdido semanal para la zafra próxima ( (en horas) |
Tiempo disponible total semanal 168 horas | Tiempo de cumplimiento de la norma potencial (168 - ( )( (en horas) |
Porcentaje del tiempo de cumplimiento de la norma potencial ( (en tanto por uno) |
| Dic | - | - | - | - | - | - | - |
| - | … | - | - | - | - | - | - |
| Mayo | - | - | - | - | - | - | - |
(Continuación)
Semana Norma potencial diaria real NP en 24h (t de caña en 24 horas) Norma potencial por 7 días real NP semana (t de caña en 7 días) Pronóstico del plan de caña a procesar semanal (PPCPs) (en t de caña por semana) Rendimiento industrial estimado semanal (en %) Pronóstico del plan de azúcar a producir Seminal (PPAPs) (en t de azúcar por semana) - - - - - - … - - - - - - - - - - -
Primero: Para la comprensión del procedimiento de cálculo desarrollado, se precisan algunos términos técnicos de la fabricación de azúcar, tales como: capacidad potencial, norma potencial, norma operacional y rendimiento industrial.
Capacidad potencial: Es la cantidad máxima de caña que puede procesar una industria azucarera moliendo estable e ininterrumpidamente durante 24 horas, de modo que se asegure el flujo estable en el proceso de obtención del azúcar (Estrada, 1987; Morales, 1993).
Norma potencial: Es la cantidad máxima de caña que puede procesar una industria azucarera moliendo estable e ininterrumpidamente durante 24 horas de acuerdo con los factores limitantes que no son la industria o los tándems (Estrada, 1987).
Esta norma se establece teniendo en cuenta los factores limitantes de la capacidad potencial.
Los factores limitantes generalmente son los referidos a la posibilidad que tiene la agricultura de entregar toda la caña que puede procesar la industria, o problemas energéticos de la fábrica. Es una necesidad ir ajustando la norma potencial a la capacidad potencial.
Norma operacional: Morales (1993), la define como el valor o la parte norma potencial que puede ser utilizada como promedio durante una zafra. En correspondencia con lo anterior Estrada (1987), plantea que se establece con relación a la norma potencial, es decir, la norma operacional es un porcentaje de la norma potencial.
A pesar de existir relación entre el tiempo perdido y el cumplimiento de la norma potencial, esta relación es más real a medida que coinciden la capacidad y la norma potencial.
Rendimiento industrial: Resume el resultado de la operación de la industria azucarera y se considera una de las verdaderas eficiencias de esta. El rendimiento industrial representa el peso de azúcar físico producido y en proceso que corresponde a cien partes en peso de caña (Estrada, 1987), se calcula usando la ecuación 8.
Ecuación 8. Rendimiento industrial.
De la ecuación 8, es posible obtener la ecuación 9, que permite calcular el peso del azúcar a producir, a partir del rendimiento industrial previamente determinado y expresado en por ciento.
Ecuación 9. Peso del azúcar a producir.
Por tanto, el rendimiento industrial estimado semanal, obtenido en la etapa dos, constituye uno de los indicadores relevantes en conjunto con el peso de la caña a procesada, que permite determinar el pronóstico del plan de producción de azúcar semanal para la zafra próxima.
Segundo: Se conoce que el pronóstico del tiempo perdido semanal (PTPs), es el resultado de multiplicar el índice de variación estacional corregida semanal (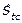
) por tiempo perdido estimado promedio semanal ().
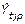Tercero: El tiempo disponible total semanal es conocido e igual a 168 horas.
Cuarto: La diferencia entre el cien por ciento de tiempo disponible total de 168 horas semanales y el pronóstico del tiempo perdido semanal (PTPs), es el tiempo de cumplimiento de la norma potencial, con lo que se podrá obtener la norma operacional de cada semana, y por consiguiente, el plan de caña a procesar semanal.
Quinto: A partir del producto de la cantidad máxima de caña que puede procesar un central moliendo estable e ininterrumpidamente durante 24 horas en siete días, que constituye la norma potencial semanal, por el porcentaje del tiempo de cumplimiento de la norma potencial (PTCNP expresado por la ecuación 10), se obtiene el pronóstico del plan de caña a procesar semanal (PPCPs) o estimado del plan de molida semanal,ecuación 11, que representa la norma operacional de cada semana.
Ecuación 10. Porcentaje del tiempo de cumplimiento de la norma potencial.
Ecuación 11. Pronóstico del plan de caña a procesar semanal.
Sexto: Del producto del pronóstico del plan de caña a procesar semanal (PPCPs), obtenido en la ecuación 11, por el rendimiento industrial estimado semanal (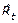
), se obtiene como resultado final el pronóstico del plan de azúcar a producir semanal, expresado por la ecuación 12.
Ecuación 12. Pronóstico del plan de azúcar a producir semanal.
A partir del cálculo del pronóstico del plan de caña a procesar y del pronóstico del plan de azúcar a producir, se obtienen las planificaciones semanales, lo que no difieren significativamente del plan para toda la zafra, pues lo que se ha hecho es prorratearlo entre cada semana de forma objetiva y fundamentada. Con ello se logra un mejor aprovechamiento de la capacidad instalada y de los recursos disponibles, tanto materiales como humanos, y un mayor control de la gestión de la industria azucarera.
Utilidad práctica de los resultados obtenidos:
El procedimiento propuesto para realizar el pronóstico y análisis del tiempo perdido, permite analizar la influencia e integración del tiempo perdido con indicadores relevantes de la planificación de zafra, tales como: norma potencial, norma operacional, aprovechamiento de las capacidades industriales, rendimiento industrial y producción de azúcar, lo que reafirma su carácter integrador en la planificación de la industria azucarera.
Los pronósticos obtenidos posibilitan realizar un ordenamiento y programación más objetiva de la caña a procesar y del azúcar a producir semanalmente, teniendo en cuenta los índices de variación estacional semanal y los rendimientos industriales semanales, aspectos estos que no se tienen en cuenta cuando se realiza la planificación mediante métodos tradicionales.
Los resultados obtenidos confirman la eficacia de los índices de variación estacional semanales para la realización de pronósticos, por tanto, la aplicación de los índices tiene efecto positivo en la planificación operativa de la industria azucarera.
Los pronósticos realizados revelan mejores resultados productivos, pues con un mismo volumen de la materia prima caña de azúcar, es posible obtener una mayor producción de azúcar con respecto al real.
Verificación de la validez de los índices de variación estacional en el pronóstico
Con el objetivo de verificar la validez y eficiencia de la información brindada por los índices de variación estacional semanal, en el pronóstico del plan de caña a procesar semanal y del pronóstico del plan de azúcar a producir semanal, se emplean las pruebas para dos muestras relacionadas de rangos de Wilcoxon y de t de Student.
Las pruebas propuestas se utilizan para comprobar si existe correspondencia entre la caña real procesada promedio semanal de las cinco zafras seleccionadas y el pronóstico del plan de caña a procesar semanal, así como, entre la azúcar real producida promedio semanal de las cinco zafras seleccionadas y el pronóstico del plan de azúcar a producir semanal.
Utilidad práctica de los resultados obtenidos:
De manera general, en este acápite donde se verifica la validez de los índices de variación estacional en el pronóstico, se concluye que mediante la aplicación las pruebas de hipótesis para dos muestras relacionadas de rangos de Wilcoxon y de t de Student, se puede afirmar que las series y las medias comparadas de la caña real procesada promedio semanal de las cinco zafras seleccionadas y el pronóstico del plan de caña a procesar semanal, e igualmente, las series y las medias comparadas del azúcar real producida promedio semanal de las cinco zafras seleccionadas y del pronóstico del plan de azúcar a producir semanal, no difieren significativamente, es decir, no existen diferencias estadísticamente significativas entre el real y el pronóstico del plan, este último calculado a partir de los índices de variación estacional semanal.
Los resultados anteriores confirman que no existen diferencias significativas en las comparaciones efectuadas, lo cual demuestra la validez de los índices de variación estacional para realizar los pronósticos de dichos indicadores productivos en el proceso de planificación.
Conclusiones
El procedimiento propuesto para realizar el pronóstico del tiempo perdido, a través de sus etapas y pasos, proporciona los elementos teóricos y prácticos necesarios para lograr la adecuada integración de los indicadores fundamentales de producción y de eficiencia en el proceso de planificación de la industria azucarera.
El tiempo perdido semanal, estimado por el método de las medias móviles, constituye un elemento básico en la elaboración y fundamentación de la programación de la zafra, en función de lograr un mejor aprovechamiento de la capacidad potencial.
El pronóstico del tiempo perdido y los índices de variación estacional, en integración con indicadores de eficiencia, posibilitan realizar el pronóstico semanal de los indicadores de producción de caña a procesar y producción de azúcar. Esto demuestra las potencialidades de la aplicación del pronóstico del tiempo perdido en la elaboración y fundamentación de los planes de producción, así como en la toma de decisiones.
