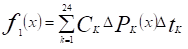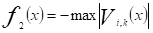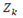Introducción
Optimal Distribution Network Reconfiguration problem consists of identifying the best radial topology by changing feeder topological structure opening sectionalizing (normally closed) and closing tie (normally open) network switches. Switching are performed with the aim of finding a radial operating configuration that optimizes certain objectives while satisfying all the operational constraints as well as all loads are energized without islanding of any node(s). Network reconfiguration is subject to other technical and operational constraints, such as radiality, node voltage limits, branch current capacity limits, and the first and second Kirchhoff’s laws (active and reactive power balance). Besides this typical formulation, network reconfiguration can also be performed primarily to improve the voltage levels, to maintain or enhance network reliability, to isolate faults more quickly, and to help prepare plans for preventive maintenance actions (Guimaraes et al., 2004). Distribution network reconfiguration is highly complex, combinatorial, non-differentiable optimization problem due to the large number of discrete switching elements. In addition, radiality constraint typically introduces additional complexity in large-sized distribution networks reconfiguration (Swarnkar et al., 2011). Obviously, greater switches number is, greater possibilities are for reconfiguration and better effects D.A.
Literature shows an extensive research work carried out in network reconfiguration area. Researches can be generally classified into conventional approaches and artificial intelligence (AI)-based approaches. Merlin A. and Back H., 1975 were the first to report a heuristic method for distribution system reconfiguration to minimize line losses. Later some other conventional approaches (Goswami et al., 1992) were developed, which include heuristic and classical optimization techniques. In Artificial Intelligence-based approaches area; (Nara et. al., 1992) introduced a genetic algorithm (GA) technique for reconfiguration of RDS with minimum loss. Later various Genetic Algorithm-based methods (Gomes et al., 2005) were developed for network reconfiguration. In fact, most of algorithms in literature are based on heuristic search techniques, using either analytical or knowledge-based engines. Several meta-heuristic techniques have been proposed to solve reconfiguration problem for loss minimization. Some of them applied genetic or evolutionary algorithms for loss minimization (Mendoza et al., 2006 and Gupta et al., 2010). Lately some other initiated-by-a-defined-individuals-number stochastic based search techniques (tentative solutions) as simulated annealing (Parada et al., 2004), taboo search algorithm (Zhang et al., 2007), ant colony optimization (Falaghi et al., 2009), particle swarm optimization (Li et al., 2008), (Abdelaziz et al., 2009), and so on, have tried to solve distribution network reconfiguration problem. When network reconfiguration problem is solved by these techniques, one of principal difficulties is radiality constraint, which ensures network radial topology with all nodes energized. Radiality constraint not only creates difficulties in initial population formation but also during intermediate evolutionary process stages. An efficient codification of these meta-heuristic techniques has remained without perfect solution for many years (Swarnkar et al., 2011). Mendoza et al., 2006 proposed a new codification strategy and accentuated crossover and directed mutation as novel genetic operators that restricted the search space (population) and diminished drastically computational time as well as minimized memory requirements. They constructed a reduced initial population of feasible individuals which is created through the branches that form “system loops.” Proposed methodology creates feasible topologies to identify system fundamental closed loops in order to originate radial topologies by creating individuals guided through fundamental loops vector. Enacheanu et al., 2008 used matroid and graph theories. Swarnkar et al., (2011) proposed a codification based upon graph theory fundamentals, which not only restricts the search space but also avoids tedious mesh checks. Proposed codification guarantees to generate only feasible radial topologies all times and is computationally efficient (Nunes Aires, 2013). Proposed Single and Multiple Link Exchange algorithms. Both insert and remove branches from network, the first one by one and the second multiple ones although - given the complexity exponential increase as branches number to insert and remove at a time increases - algorithm restricts itself to two branch exchange at a time. They considered that all branches could be removed, as long as restrictions are fulfilled. Process ends in both cases, when the least losses or optimal configuration is found. For active power losses calculation, it is necessary that a load flow be carried out in each reconfiguration.
The Non-dominated sorting genetic algorithm-II (NSGA-II)’s arrangements and a new coding used, implemented in MatLab, creates randomly initial population for genetic algorithm by using a heuristic approach and genetic operators for generating feasible individuals during initialization, crossover and mutation are modified and adapted with the graph theory's help for transforming initial population's infeasible individuals which not satisfied radiality constraint as well as for avoiding infeasible individual’s generation during each stage of the genetic evolution. Although procedure steps for obtaining feasible individuals as well as fundamental loops system concept's employment is very similar to one used by other authors (Gupta et al., 2010), (Swarnkar et al., 2011), (Mendoza et al., 2006), coding proposed is completely and absolutely new and newfangled and avoid utilizing either of modified genetic operators: Accentuated crossover and directed mutation (Gupta et al., 2010), or modified crossover and mutation (Swarnkar et al., 2011).
Materials and methods
In conventional Genetic Algorithms (GA), initial population that is randomly created, consists of a large number of infeasible individuals (violate radial constraint), particularly in medium and large distribution networks. In the proposal, these infeasible individuals are transformed into feasible ones using graph theory. Fundamental loops are determined for mesh network by closing all tie switches. Fundamental loops number in meshed network is equal to system tie switches number and is given by the relationship.
Therefore, chromosome length for genetic algorithm is L. Each gene on a chromosome, denoted by a real number, will be the switch that will be open to maintain a feasible radial configuration.
Proposal changes genetic operators, “accentuated crossover” and “directed mutation” proposed by (15) to generate feasible individuals during initialization, crossover, and mutation. “Loop vectors”, “common branch vectors” and “‘prohibited group vectors” are also employed to avoid infeasible individuals’ generation during each genetic evolution stage. Steps to obtain feasible individuals are:
Obtain all meshed network fundamental loops. Loop vectors L k are created, containing the set of elements of the kth fundamental loops K=1,2,….,L
Determine all common branch vectors, L i that contain the set of common elements between two loop vectors L j* and L j* .
Determine all prohibited group vectors (set of common branch vectors) R m1,m2,m3……, which isolate the main node(s) of the distribution network.
Let Z k be the kth gene of a chromosome, then for this chromosome to be feasible, following rules must be satisfied: m 1, m 2, m 3 …..
Rule 1 avoids any node isolation located on the distribution network perimeter, while Rule 2 and Rule 3 avoid node isolation inside distribution network. Therefore, when encoding individuals, these three rules ensure distribution network radial topology without forming islands of any one node(s). In general, genetic chromosomal coding in real numbers can be defined as: Z 1 L 1 Z 2 L 2……… Z k L k ……Z L L L
Problem Formulation
Proposed method formulates distribution networks reconfiguration as a multi-objective optimization problem that pursues optimal set of branches selection to open in order to obtain the minimum system operating cost and the maximum voltage in load nodes. Solutions are subject to being feasible radial configurations.
Independent Variables
Problem’s independent variables, represented by array x, are the branches set that must be open to obtain a radial configuration for the distribution system. For a meshed network of N nodes and M branches, the branches number to be open in order to obtain a radial configuration is equal to the fundamental loops number L (Equation 1).
Constrains
The main problem limitation is that any reconfiguration solution must be a radial circuit. In order to fulfill this constraint, meshed network graph must be examined to determine loop vectors L, common branch vectors C, and prohibited group vectors R N. (Gupta et. al., 2010). Each loop vector Lk contains the branches set of the kth graph fundamental loop. Furthermore, each common branches vector Ck(i,j), is the branches set at the loop vectors intersection Li and Lj. On the other hand, if n is a main node set, prohibited group vector Rk(n) is the m vectors common branch set which, if all are open, isolate the node set from the circuit. In that way, if x is the branches set to be open, following three rules stated by (Gupta et. al., 2010) must be met to obtain a feasible radial configuration (Viewed in the steps to obtain feasible individuals).
Objective Functions
Although other objective functions can be considered, in essence proposed optimization problem can be formalized by means of two objective functions: minimum system operation cost f1(x) and maximum load nodes voltage f2(x).
System operation cost is mainly related to energy losses cost in network conductors. Energy losses variable costs as well as a variable daily load demand are considered in the proposed method.
Where:
C
k
($/kWh) Energy cost in hour 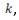
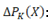 Network power losses in hour
Network power losses in hour 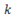 and in every
and in every 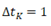 hour.
hour.
For comparison purposes with literature, energy cost factors used were taken from reference (S. S. F. Souza et al., 2016).
Network power losses 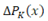 are variable for different load states. Again, a daily load variation curves set is used for residential
are variable for different load states. Again, a daily load variation curves set is used for residential 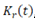 commercial
commercial 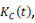 , and industrial
, and industrial 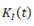 customers, to represent loads variability. Curves are used for both active and reactive load. For instance, if load at node i is represented by a residential-type curve, load at this node at hour
customers, to represent loads variability. Curves are used for both active and reactive load. For instance, if load at node i is represented by a residential-type curve, load at this node at hour  .
.
For convenience, at-load-nodes voltage maximization can be expressed as negative maximum voltage minimization, thus, second objective function is defined by:
Voltages and power losses determination for different load states is achieved by a load flow function.
Optimization Algorithm
Among most successful multi-objective optimization methods are Non-Dominated Sorting Genetic Algorithm family among which is the NSGA-II. Like every genetic algorithm, a particular problem resolving by NSGA-II implies some adaptations and certain algorithm parts reprogramming. In this case, real coding algorithm NSGA-II implemented in MatLab (Seshadri, 2012). Has been adapted for solving electrical network reconfiguration. Proposed method was executed on a DESKTOP-B29S0MC Intel(R) Core(TM) i5-8350U CPU @ 1.70GHz, 1.90 GHz computer with 8.00 GB (7.86 GB usable) Installed RAM.
In order to obtain viable radial system configurations, branches selection to open is subject to compliance with three rules, which have been explained above. First Mendoza et al. (2006) and later Gupta et al. (2010) employed an integer-composed chromosome that directly selects a single branch to open from each fundamental loop vector. Modified genetic operators to generate feasible individuals during initialization, crossover, and mutation were used by them. These operators transform an infeasible chromosome to obtain a feasible one. Instead, using a coding that ensures chromosome viability for all gene values have been the employed approach in proposed method. That way, crossover and mutation don't need special genetic operators.
Chromosome Coding
In the proposal, chromosome is represented by a real values (genes) array z, where each value ZK (0-≤ ZK ≤ 1), determines X j problem independent variable (kth branch to open). However, independent variables determination depends on sequence in which genes z are decoded in the x selected branches set. The procedure is the following:
All branches are closed and available to open.
Available branches set in fundamental loop vector
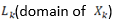 is determined by:
is determined by: 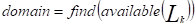 (4)
(4)Corresponding branch
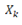 is selected from the available domain by:
is selected from the available domain by: 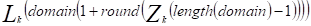 (5)
(5)Selected
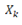 branch is open and marked as unavailable for further selection.
branch is open and marked as unavailable for further selection. A common branch vector containing an open branch will be marked as open and all its branches will be marked as unavailable for further selection.
All branches of a prohibited group vector with all but one open common branch vector will be marked as unavailable for further selection.
Instead of encoding variables as an integer, which is logical, because they correspond to branches number, proposal encodes variable as a real number between 1 and 0
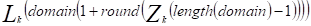 where zero is the first prohibited loop switch and one (1) the last one.
where zero is the first prohibited loop switch and one (1) the last one. 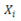 is an arbitrarily selected value. This avoids making Gupta’s modifications [19]. Then, by simple linear expression, the closest number to the real number obtained is searched (Equation 5).
is an arbitrarily selected value. This avoids making Gupta’s modifications [19]. Then, by simple linear expression, the closest number to the real number obtained is searched (Equation 5).
An arrangement called “isvar” was made that identifies if that variable is available to work with and at the beginning, all of them were given a value one (1), i.e., all values could be selected. If variable state is zero (0) it means that switch is open and if it is one (1) it means that it is closed. Each value of X
i
is the real value generated randomly for i variable (i.e., for the first variable, it is X
i
, so “vars” would mean: What are loop variables being analyzed?). For variable i it is the fundamental loop i. But not all possible variables are analyzed, but only those that 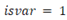 .
.
Available variables are checked. Which ones that have 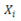 are searched, that at the beginning are all of them, because to all is assigned a value of 1.
are searched, that at the beginning are all of them, because to all is assigned a value of 1.
Illustrative Example
As illustrative example, procedure to determine Xj problem independent variable (kth branch to open), is shown below:
For the First Fundamental Loop
For example, in 33-bus test distribution systems, for the first loop, there are ten variables that are switches 2, 3, 4, 5, 6, 7, 33, 20, 19 and 18. For the 10 variables,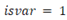 , thus, all are available. Figure 1 depicts 33-bus test distribution system loop 1’s switches and branches.
, thus, all are available. Figure 1 depicts 33-bus test distribution system loop 1’s switches and branches.
Figure 2 shows loop 1's each switch number, all of them with isvar = 1 that mean they are all closed and could be selected. Besides, variables number (vars = 1 …10) from which through equation (1 + Xi (variables number) - 1) is determined the switch selected to open. In addition, switch selection to be open is shown for 0, 1, 0.5 values of Xi.
 Source: own elaboration
Source: own elaborationFig. 2 - Procedure to select the switch to be open for 0, 1, 0.5 values of Xi
Vars = 1 … 10
If variable state is zero (isvar = 0), it means that switch is open.
Variable Xi comes with a value. Therefore: = 1 + Xi (variables number) - 1) and that value is rounded.
If Xi = 0 it would be: = 1 + 0 ((10) - 1) = 1 + 0 = 1. The first switch would be selected which is number 2.
If Xi = 1 it would be: = 1 + 1 ((10) - 1) = 1 + 9 = 10. The last switch would be selected which is number 18.
If a Xi intermediate value were obtained, with equation 1 + round (Xi (length (var) - 1)), variable with integer number (switch) with which it is going to work is selected (because it is rounded) and that value is assigned to loop array, which selects which variable is.
Once switch to be opened has been selected, start of that variable is marked zero (0) to indicate that this switch opened but also that it can no longer be used.
If Xi = 0.5 it would be: = 1 + 0.5 ((10) - 1) = 1 + 4.5 = 5.5 ≈ 6. Sixth switch would be selected which is number 7.
For example, in Figure 3, if switch 18 is that opens: stat (18) = 0 to indicate that this variable (switch) opened; isvar (18) = 0 so that variable cannot be used anymore. Thus, switch 18 can never be selected again. This avoids an infeasible variable.
MatLab Arrays
function stat = decode(self,x)
x(x < 0) = 0;
x(x > 1) = 1;
M = size(self.branches,1);
MT= size(self.lnodes,1);
stat = ones(MT,1);
isvar = zeros(MT,1);
isvar(1:M) = 1;
for i = 1: length(x)
% select possible branches to be disconnected in the loop
loop = self.loops{i};
vars = find(isvar(loop));
% select branch
k = loop(vars(1 + round(x(i) * (length(vars) - 1))));
% the selected branch is disconnected
stat(k) = 0;
isvar(k) = 0;
Genetic Operators
Taking into account that chromosome is always feasible for real numbers within limits 0 < Xi < 1, there is no need to use special genetic operators as already stated.
In proposed method, 60% of offspring population is obtained by crossover, for which a scattered crossover operator is used. Operator creates a set u half the chromosome size, uniformly randomly sampled. The first offspring selects genes from the first parent that are not in u and genes from the second parent that are in u. The second descendant inverts selection. Remaining 40% offspring population is obtained by mutation, for which a uniform mutation operator is used. Operator mutates 2% genes on the uniformly randomly sampled chromosome. Each gene mutates by a normally distributed random number using a 0.1 mutation step.
Objective Functions Calculations
A special NSGA-II part that must be reprogrammed to solve the presented problem is a procedure for computing objective functions f1(x) and f2(x). This procedure, named Evaluate_objectives (x), is called by NSGA-II algorithm each time a new individual is produced by crossover or mutation. The parameter (x) which passed to this procedure is the chromosome.
Procedure developed for Evaluate_objectives (x), executes following steps:
Results and discussion
Table 1 shows a comparison of 33-bus test system obtained results (Mahdavi et. al., 2021) with other methods.
Table 1 - Comparison of 33-bus test system obtained results with other methods
| Methods | Run time (s) | Open switches | Initial Losses (kW) | Losses after Reconfiguration (kW) |
|---|---|---|---|---|
| Based on optimal power flow using benders decomposition (J. A. Taylor et al., 2012). | 0.11 | 7, 9, 14, 32, 37 | 202.54 | 139.55 |
| Convex models using quadratically programming (J. A. Taylor et al., 2012). | 0.21 | 7, 9, 14, 32, 37 | 202.7 | 139.55 |
| Efficient simulated annealing (Y. J. Jeon et al., 2002). | 0.34 | 7, 9, 14, 32, 37 | 202.7 | 139.55 |
| Simulated annealing algorithm (Y. J. Jeon et al., 2002). | 0.3 | 7, 9, 14, 32, 37 | 202.7 | 139.55 |
| Mixed-integer linear program model (F. Llorens Iborra et al., 2012). | 1.0 | 7, 9, 14, 32, 37 | 202.68 | 139.55 |
| Convex models using quadratically constrained Program (J. A. Taylor et al., 2012). | 1.43 | 7, 9, 14, 32, 37 | 202.7 | 139.55 |
| New branch Exchange Heuristic algorithm (F. V. Gomes et al. 2005). | 1.66 | 7, 9, 14, 32, 37 | 202.68 | 139.55 |
| Discrete ascent optimal programming (F. V. Gomes et al. 2005). | 1.99 | 7, 9, 14, 32, 37 | 202.68 | 139.55 |
| Fast reconfiguration considering loss minimization (H. P. Schmidt et al., 2005). | 0.01 | 7, 9, 14, 28, 31 | 194.53 | 142.03 |
| Fast reconfiguration considering loss minimization D. Shirmohammadi et al., 1992). | 0.14 | 7, 10, 14, 32, 31 | 202.68 | 140.26 |
| A new approach using optimum power flow and sensitivity analysis (F. V. Gomes et al. 2006). | 1.99 | 7, 10, 14, 32, 37 | 202.68 | 140.26 |
| Proposed | 4.31 | 6, 9, 14, 36, 37 | 139.46 | 96.39 |
Source: own elaboration
Table 2 - Comparison of 70-bus test system obtained results with other methods.
| Methods | Average computing time (s) | Number of global optimal reached in 100 runs | Open switches | Real power loss (kW) |
|---|---|---|---|---|
| Hybrid genetic particle swarm optimization algorithm (C. Zhang et al., 2007). | 43 | 100 | 14, 59, 62, 70, 71 | 99.70 |
| Simulated annealing (H. D. Chiang et al., 1990) | 36 | 95 | 14, 57, 62, 70, 71 | 99.70 |
| Enhanced genetic algorithm-based fuzzy multi-objective approach Y. C. Huang (2002). | 13 | 97 | 13, 59, 70, 71, 74 | 122.90 |
| Adaptive genetic algorithm in fuzzy framework (N. Gupta et al., 2010) |
8 | 100 | 15, 58, 62, 70, 71 | 99.60 |
| Proposed | 7.89 | 57 | 12, 56, 63, 69, 70 | 53.88 |
Source: own elaboration
Both results shown in the above tables (table 1 and 2) show that non-dominated sorting genetic algorithm-II arrangements and coding proposal application provides a promising tool for optimal electrical distribution networks reconfiguration taking into consideration that unlike researcher’s precedent the proposal neither does not need to modify the answer when individual’s generation is infeasible nor for avoiding new infeasible individual’s generation. In addition, the use of special genetic operators is not necessary. Proposal does not make modifications and get reducing search space and computational burden.
Conclusion
An efficient coding of meta-heuristic techniques has remained without perfect solution for many years. The coding proposal is adapted by using graph theory help for generating feasible individuals as well as for transforming each infeasible individual in feasible (radial networks), in each stage of the genetic evolution. In addition, considering that chromosome is always feasible for real numbers within limits 0 < Xi < 1, there is no need to use special genetic operators as already stated.
Unlike (Mendoza et. al., 2006) new coding proposal not only search to isolate external nodes but also internal ones during feasible individual’s generation. In contrast to (Gupta et. al., 2010) which modify the answer when this is infeasible by executing an accentuated crossover process to make it feasible, proposal does not make modifications. In the Non-dominated sorting genetic algorithm-II arrangements proposed, no genetic algorithm modification needs to be made. Once switch that will be open is selected, it will no longer can be used, thus, variant number to be used is reduced considerably. In addition, infeasible variants are avoided, therefore computational time is reduced.
In contrast to authors mentioned above, that employed an integer-composed chromosome that directly selects a single branch to open from each fundamental loop vector as well as modified genetic operators, the use a coding that ensures chromosome viability for all gene values have been employed. That way, crossover and mutation don't need special genetic operators.
Non-dominated sorting genetic algorithm-II arrangements and coding proposal application results, implemented in MatLab show that proposal provides a promising tool for optimal electrical distribution networks reconfiguration. Other objective functions can be considered without any additional computational burden. Proposal effectiveness has been tested with 33-bus and 70-bus test distribution systems and results are a promising tool for optimal electrical distribution networks reconfiguration and better than precedent proposals.
Future Work
Notwithstanding previous results, author’s work continues on coding perfecting and improvement for genetic algorithms used in optimal distribution network reconfiguration and especially, on the improvement of NSGA-II algorithm, for its future use as an effective method in network reconfiguration.