Artículo Original

DETERMINACIÓN DE LOS COEFICIENTES DE TRANSFERENCIA DE CALOR EN CALENTADORES DE JUGO DE CAÑA

DETERMINATION OF HEAT TRANSFER COEFFICIENTS IN SUGAR JUICE HEATER

Alién Acosta Alvarez¹  , José Ángel Vázquez Llanes¹  , Isnel Benítez Cortés^{2  *}  , Carlos Romero Perdomo³ 

¹UEB Central Azucarero “Siboney”, Batey Siboney, Sibanicú, Camagüey, Cuba.

²Departamento de Ingeniería Química, Universidad de Camagüey “Ignacio Agramonte y Loynaz”. Carretera Circunvalación Norte km 5½, Camagüey, Cuba.

³Departamento de Ingeniería Mecánica, Universidad de Camagüey “Ignacio Agramonte y Loynaz”. Carretera Circunvalación Norte km 5½, Camagüey, Cuba.

RESUMEN

En el presente trabajo se determinan los coeficientes de transferencia de calor y el factor de incrustaciones en calentadores de jugo de caña. Se realizan mediciones de caída de presión en el tiempo así como las temperaturas de entrada y salida del jugo de caña y el vapor. Se determinan los coeficientes globales de transferencia de calor y se comparan con los criterios de la literatura para la estimación del régimen de ensuciamiento. Su aplicación en el central “Siboney”, permite obtener los niveles de reducción del coeficiente de un 42% al 50%, para los intercambiadores A y B, respectivamente, a los 15 días de operación.

Palabras-clave: azúcar; guarapo; incrustaciones; intercambiador de tubo y coraza; limpieza

ABSTRACT

In present work, the heat transfer coefficients and the incrustation factor of the cane juice are determined. Measurements are made, as well as inlet and outlet temperatures of cane juice and steam. The heat transfer global coefficients are determinate and compared with the literature criteria for the estimation of the incrustation regime. Its application in "Siboney" plant, allows to obtain levels of coefficient reduction of 42% and 50% for the heat exchanger A and B, respectively, in 15 days of operation.

Key words: sugar; sugar cane juice; incrustation; tube and shell exchanger; cleaning

1. INTRODUCCIÓN

En el central azucarero “Siboney” se vienen presentando problemas con la transferencia de calor en los intercambiadores de tubo y coraza que se encargan de calentar el jugo mezclado. Dificultades en la molida por las altas temperaturas del agua de imbibición (aproximadamente 100ºC) indica, entre varios factores, un elevado nivel de obstrucción en las líneas internas de guarapo, debido a la abundante formación de incrustaciones. Esto provoca que el agua de imbibición funda la cera contenida en la caña, las mazas se embotan y patinan, se acumulan grandes cantidades de meollo en las bandejas y se mantiene latente el riesgo de que el bandejero sufra un accidente, acelerando el desgaste de las mazas. Por tanto, el objetivo de este trabajo es determinar la variación de los coeficientes de transferencia de calor así como el factor de obstrucción del intercambiador de calor en el tiempo. Para esto se requiere de la implementación de un procedimiento que se describe a continuación.

1.1. Balance de masa

Se tuvieron en cuenta las corrientes de entrada y salida despreciando la acumulación:

$\sum \left(w_E\right)=\sum \left(w_S\right) \left(1\right)$

Donde w representa cada flujo de masa, caliente y frío respectivamente. Como en este equipo no existe contacto directo entre las corrientes, los flujos permanecen constantes, de modo que:

$w_{cE}=w_{cS}y w_{fE}=w_{fS}{}_{ }\left(2\right)$

1.2. Balance de energía

Se establece que el calor cedido Qced (kW) es la sumatoria del calor absorbido Qabs (kW) más el calor cedido al ambiente por convección y radiación Qrad (kW):

$Q_{Ced}=Q_{Abs}+Q_{Rad}=w_{fS}C{p}_f\Delta T_f+w_{cS}C{p}_c\Delta T_c \left(3\right)$

Donde:

Cpc,f	- capacidad calorífica del fluido caliente y el frío, respectivamente (kJ/kg^oC)
Δc,f	- diferencia de temperaturas del fluido caliente y frío, respectivamente (^oC)

Para el caso específico de las soluciones de sacarosa en la industria azucarera, los valores de capacidad calorífica Cp (kJ/kg^oC), coeficiente de transferencia de calor del jugo k (W/m²·ºC), viscosidad a temperatura media µ (Pas) y densidad del jugo ρ (kg/m³) pueden calcularse según la tabla 1.

Tabla 1 Determinación de las propiedades físicas del jugo 

Ecuación	Bibliografía	Número
$C{p}_f=\mathrm{4,1868}-\mathrm{2,5121}·{10}^{-2}\text{º}Bx$	(Hugot, 1986); (Mendieta y Escalante, 2013)	(4)
${\mu }_f=\frac{\mathrm{1528,87094}-\mathrm{0,6924}t-\mathrm{0,103}{k}_f}{1000}$	(Lamela y col., 1999)	(5)
$k_f=\frac{\frac{T_{mj}}{\mathrm{0,1}+\frac{\mathrm{0,08}}{\frac{Gt}{\rho }}}}{1000}$	(Hugot, 1986)	(6)
${\rho }_f=1000\left(\mathrm{0,956}-\mathrm{0,005}\text{º}Bx\right)$	(Mendieta y Escalante, 2013)	(7)

Donde: Bx: grados Brix del jugo (^oBx); t: tiempo transcurrido desde la última limpieza (días); Tmj: temperatura media (^oC).

1.3. Evaluación energética

Se determina el coeficiente de transferencia de calor U en una superficie de intercambio incrustada, a partir del coeficiente de transferencia de calor de la superficie sin incrustaciones (U₀). Este depende del ancho de la incrustación δ_b (m) y de la conductividad térmica de la incrustación λ_b (W/m^oC):

$U=\phi U_0 \left(8\right)$

$\phi =\frac{1}{\frac{1+{\delta }_b}{{\lambda }_b}{U}_0} \left(9\right)$

Para estimar los valores de los coeficientes de transferencia en el tiempo, se comparó el comportamiento real con el calculado a través de diferentes modelos. Algunos de ellos toman en consideración, no solamente la velocidad y la temperatura del jugo, sino también la geometría de los tubos y el tiempo transcurrido después de la última limpieza, como el de Wright reportado por ^{Batule (2009}).

$\frac{1}{U}=\frac{d^{\mathrm{0,25}}}{\mathrm{4,35}}+\frac{1}{\mathrm{13,5}}+\mathrm{0,0035}{t}^{\mathrm{0,8}}\left(1+\frac{\mathrm{10,763}}{v^3}\right)+\frac{1}{\mathrm{0,283}{d}^{\mathrm{0,2}}{v}^{\mathrm{0,8}}{T}_{mj}^{\mathrm{0,467}}} \left(10\right)$

Donde:

d	- diámetro interior de los tubos (m).

^{Hugot (1986}) propone una ecuación que también considera el tiempo (en días) transcurridos desde la última limpieza:

$U=U_0{\left(\frac{a}{a+j}\right)}^{\mathrm{0,5}}\left(11\right)$

Donde: a: coeficiente que depende de la rapidez de la incrustación, j: días transcurridos desde la última limpieza (días). Para calentadores tubulares comunes el parámetro "a" toma los valores de 6 para condiciones favorables, 4 para condiciones intermedias y 3 para condiciones desfavorables.

2. MATERIALES Y MÉTODOS

Se trabajó con el calentador líquido-líquido instalado, pasando jugo por los tubos y agua caliente por la coraza, el cual consta en su diseño original con dos cuerpos de tubo y coraza de tipo 1-2 y 1-4 conectados en serie y con 76 tubos de 32 mm y 5,75 m de longitud cada uno. Este se encarga de elevar la temperatura del guarapo de 35 a 50 ⁰C disminuyendo la temperatura del agua que luego se utiliza en la imbibición (^{Hugot 1974}). La figura 1 muestra el intercambiador.

Figura 1 Intercambiador de calor con sus dos cuerpos 

La metodología empleada se basa en un análisis del incremento paulatino de los efectos del ensuciamiento en los equipos durante el funcionamiento normal, siendo esta evolución diferente en cada equipo, en función de la naturaleza de las corrientes que intervienen y las características constructivas del mismo (^{Berraquero, 2003}). Este método establece una serie de parámetros a considerar como indicadores de condición, basados en el procedimiento desarrollado por ^{Kern (1999}) para el diseño y evaluación de intercambiadores de calor.

Por conveniencia, los cálculos se basan en la corriente que circula por los tubos, ya que esta solo intercambia calor con la corriente de la carcasa, no presenta pérdidas energéticas al ambiente, y son más pronunciados los efectos de la variación de la geometría de la sección de flujo (^{González, 2012}). El procedimiento a seguir es el siguiente:

1. Determinar las características constructivas y de operación inherentes al diseño del intercambiador.

2. Tomar los datos de campo (flujos, temperaturas, composición del jugo) y dar seguimiento al comportamiento del equipo bajo condiciones de estabilidad, (coeficientes de transferencia e incrustación, eficiencia).

3. Comparar el valor del coeficiente de ensuciamiento del intercambiador con el valor en el inicio del ciclo, cuando se encuentra limpio. En caso de que el nivel de ensuciamiento tome un valor relativamente elevado, se considera la posibilidad de someter el equipo a un proceso de limpieza.

4. Comparar el comportamiento del coeficiente de transferencia con los modelos matemáticos reportados en la literatura, seleccionar el más acorde al comportamiento observado.

Con los datos recogidos, y después de realizar el correspondiente balance de energía, se procede a hallar la diferencia real de temperatura, en función de la Media Logarítmica de la Diferencia de Temperatura (^oC):

$\Delta T=F_{T}MLDT=F_T\frac{T_{C1}-T_{f2}-T_{C2}+T_{f1}}{ln\left[\frac{T_{C1}-T_{f2}}{T_{C2}-T_{f1}}\right]} \left(12\right)$

La mayoría de los autores determinan el valor de F_T (adimensional) a partir de diagramas en función de R y S (adimensionales) (^{Kern, 1999}). También puede calcularse, para intercambiadores 1-2n, por la ecuación (^{Moncada, 2005}):

$F_T=\frac{\sqrt{\left(R^2-1\right)}ln\left[\frac{1-S}{1-RS}\right]}{\left(R-1\right)ln\left[\frac{2-S\left(R+1-\sqrt{\left(R^2-1\right)}\right)}{2-S\left(R+1+\sqrt{\left(R^2-1\right)}\right)}\right]} \left(13\right)$

Donde:

$R=\frac{T_{C1}-T_{C2}}{T_{f2}-T_{f1}}$ y $S=\frac{T_{f2}-T_{f1}}{T_{C1}-T_{f1}} \left(14\right)$

Conocidos los datos del equipo, se calcula el coeficiente de transferencia de calor total (W/m^2·ºC) (^{Dahake, 2013}; ^{Reyes y col., 2014}) donde A es el área de transferencia de calor (m²):

$U=\frac{Q}{A{F}_{T}MLDT}\left(15\right)$

Para determinar la caída de presión en los tubos ΔP_t (Pa):

$\Delta P_t=N_T\left[8f_t\left(\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$D_{itub}$}\right.\right){\left(\raisebox{1ex}{$\mu $}\!\left/ \!\raisebox{-1ex}{${\mu }_w$}\right.\right)}^{-m}+\mathrm{2,5}\right]\left[\frac{\rho v_t{}^2}{2}\right]\left(16\right)$

Donde:

Nt	- número de tubos
ft	- Factor de fricción en tuberías (adimensional)
L	- Longitud de tuberías (m)
Diturb	- Diámetro interior del tubo (m)
μw	- Viscosidad a temperatura de la pared (Pa·s)
m	- Coeficiente (adimensional)

El valor del coeficiente f para el caso de los tubos se busca según el valor del Número de Reynolds (adimensional) determinado a temperatura media de la corriente (^{Kern, 1999}).

$R{e}_t=\frac{{\rho }_t{v}_t{D}_{itub}}{{\mu }_t}$ (17)

El coeficiente “m” también depende del régimen de flujo, siendo igual a 0,25 para Re<2100 y 0,14 para Re>10000. Para determinar la caída de presión en la coraza se parte del área de flujo (m²):

$a_{cor}=\frac{D_{cor}CB}{P_t}$ (18)

Donde C es el espacio entre los tubos $C=P_t-D_{etub}$ (m) y D_cor el diámetro de la coraza (m²). El valor del diámetro equivalente, teniendo en cuenta el arreglo triangular, se calcula como:

$D_e=\frac{4\left(\mathrm{0,86}{P}_t{}^2-\pi \frac{D_{etub}{}^2}{4}\right)}{\pi D_{etub}}$ (19)

Luego la velocidad másica en la coraza G_cor (kg/m^2·s) se determina por:

$G_{cor}=\raisebox{1ex}{$w_{cor}$}\!\left/ \!\raisebox{-1ex}{$a_{cor} \left(20\right)$}\right.$

$R{e}_{cor}=\frac{G_c{D}_e}{{\mu }_c} \left(21\right)$

Con este valor, la segmentación y el tipo de arreglo es posible localizar el valor de f_cor de forma gráfica y calcular:

$\Delta P_{cor}=8f_{cor}\left(\raisebox{1ex}{$D_{cor}$}\!\left/ \!\raisebox{-1ex}{$D_e$}\right.\right)\left(\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$B$}\right.\right){\left(\raisebox{1ex}{$\mu $}\!\left/ \!\raisebox{-1ex}{${\mu }_w$}\right.\right)}^{-m}\left[\frac{\rho v_c{}^2}{2}\right]\left(22\right)$

Para la coraza puede considerarse (^{Moncada, 2005}):

$v_{cor}=\frac{G_c}{\rho }\left(23\right)$

Estos valores representan las diferentes caídas de presión en cada corriente según el diseño del equipo en condiciones ideales, por lo que pueden emplearse como referencia para valorar la condición de este parámetro durante la explotación. Varios autores consideran que, en ambos casos, el término $\left(\raisebox{1ex}{$\mu $}\!\left/ \!\raisebox{-1ex}{${\mu }_w$}\right.\right)$ es despreciable y puede omitirse, dada la similitud en los valores de µ y µ_w (^{Kern, 1999}; ^{Moncada, 2005}; ^{Kern, 2005}; ^{Segura, 2012}).

La influencia de las incrustaciones en la pérdida de eficiencia de los intercambiadores de calor se determina mediante el coeficiente global de transferencia de calor, en función de los parámetros de entrada y salida del equipo (^{Torres y col., 2011}).

$U=\frac{w_{c}C{p}_c\left(T_{ec}-T_{sc}\right)}{A\left[\frac{\left(T_{ec}-T_{sf}\right)-\left(T_{sc}-T_{ef}\right)}{ln\left(\frac{T_{ec}-T_{sf}}{T_{sc}-T_{ef}}\right)}\right]}\left(24\right)$

Mediante un ajuste del tipo exponencial asintótico se obtiene la supuesta curva de ensuciamiento. Al comparar la curva con los valores obtenidos mediante los modelos matemáticos reportados en la literatura es posible determinar cuál de estos describe mejor el comportamiento de la variable. Con esta información se puede estimar, con mayor precisión, el comportamiento futuro de la unidad ante cambios en los caudales y temperaturas.

El factor de ensuciamiento e incrustaciones R_d (m²ºC/W) se obtiene mediante la comparación del valor del coeficiente global de transferencia de calor, obtenido de forma experimental cuando el equipo está limpio (U_máx), con los valores experimentales de la ecuación en función del tiempo (^{Torres y col., 2011}).

$R_d=\frac{U_{m\text{á}x}-U}{U_{m\text{á}x}U} \left(25\right)$

3. RESULTADOS Y DISCUSIÓN

3.1. Calor transferido en el tiempo

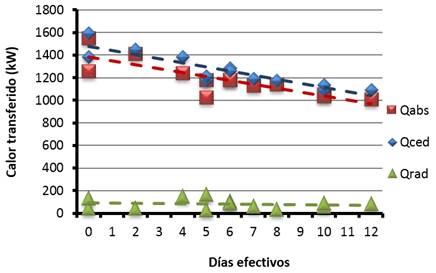
La disminución en el calor absorbido por el guarapo está dada por la formación de capas de partículas incrustantes en el interior de los fluses del calentador. Estas capas se caracterizan por poseer altos valores de resistencia térmica y actúan como material aislante, dificultando la transferencia de calor agua-jugo. Por su parte, el aumento del calor transferido al medio se debe fundamentalmente al descenso de las temperaturas del ambiente. Por ello, la tendencia del calor cedido por el agua caliente es hacia la disminución. La Figura 2 muestra el comportamiento de la transferencia de calor en el tiempo.

Figura 2 Comportamiento del calor transferido en el tiempo 

3.2. Coeficientes de transferencia de calor

En la Figura 3 se muestra el comportamiento del coeficiente de transferencia en cada cuerpo del intercambiador estudiado. Para el cuerpo “A” se aprecia que el modelo propuesto por ^{Hugot (1986}), en su variante para condiciones favorables presenta buen ajuste (R²=98,47%), mientras que el “B” se asemeja más a la variante para condiciones intermedias (R²=97,73%). En ambos casos se ha considerado el tiempo de operaciones como los días efectivos.

La diferencia en el comportamiento está dada por la posición relativa de los cuerpos. El cuerpo “B” se ensucia más rápidamente pues es quien recibe el jugo crudo directamente desde los molinos, lo que significa que tiene mayor cantidad partículas incrustantes. En el cuerpo “A” se depositan aquellas partículas que no llegaron a hacerlo en el cuerpo “B”, siendo ligeramente menor su cantidad.

Figura 3 Comportamiento del coeficiente de transferencia de calor 

3.3. Factor de ensuciamiento

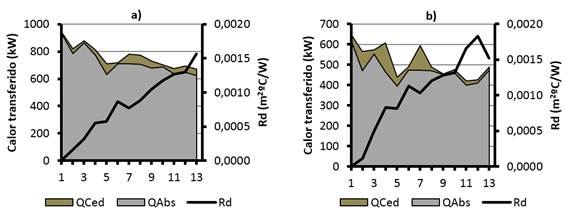
A medida que transcurre el tiempo, la cantidad de calor transferido disminuye al mismo tiempo que el factor de ensuciamiento aumenta (ver Figura 4). Al cabo de 12 días efectivos los valores de R_d alcanzan el límite de 0,00020 m^2oC/W reportado para la categoría de “Líquidos orgánicos”. Ello trae aparejado un aumento en la cantidad de fluido caliente en etapas posteriores a fin de suministrar la energía necesaria para el proceso fabril, lo que a su vez redunda en un aumento del consumo de combustible y costos asociados. Según estos modelos:

$U=\mathrm{0,579}{U}_0\text{para a}=6\text{y}U=\mathrm{0,5016}{U}_0\text{para a}=4\left(26\right)$

Ello significa que, al cabo de dos semanas, el coeficiente de transferencia del cuerpo “A” habrá disminuido un 42%, y el del “B”, 50%.

Figura 4 Relación calor transferido - factor de incrustación: a) Cuerpo A, b) Cuerpo B 

4. CONCLUSIONES

1. Los valores del coeficiente de transferencia de calor obtenidos disminuyen a medida que el tiempo transcurre debido al incremento de las incrustaciones. Su comportamiento se ajusta a los modelos reportados por ^{Hugot (1986}), comportándose como condiciones favorables e intermedias, para el cuerpo “A” y “B”, respectivamente.

2. Los niveles de reducción del coeficiente de transferencia de calor están en el orden del 42% para el cuerpo “A” y del 50%, para el cuerpo “B”.

3. El tiempo para alcanzar el nivel límite del factor de obstrucción está en el orden de los 12 días de trabajo, lo que sugiere este tiempo como el requerido para realizar un proceso de limpieza de los intercambiadores de calor.

4. La transferencia de calor así como el coeficiente de transferencia de calor que la caracteriza disminuyen con el tiempo de explotación del intercambiador, siendo de forma contraria para el caso del factor de ensuciamiento.

REFERENCIAS

Batule, E., Serie Azucarera. Calentadores de jugo., Vol. 12, MINAZ, 2009, pp. 106-163.

Berraquero, F., Metodología para determinar los ciclos de limpieza, Folleto, 2003, pp. 1-5.

Dahake, M., Heat transfer laboratory manual, Aurangabad, Mahatma Gandhi Mission’s Jawaharlal Nehru Engineering College., India, 2013, pp. 1-59.

González, R., Diseño de un intercambiador de calor de carcasa y tubos, Folleto, Editorial Universidad de Camagüey, 2012, pp.1-16.

Hugot, E., Manual para ingenieros azucareros., Editorial Continental SA, 1974, pp. 225-242.

Hugot, E., Handbook of sugar cane engineering, Editorial Elsevier Science Publisher, Holanda, 1986, pp. 296-330.

Kern, D., Procesos de transferencia de calor., México, Editorial Continental SA, 1999, pp. 131-213.

Kern, D., Procesos de transferencia de calor. La Habana. Editora Revolucionaria, 2005, pp. 159-230.

Lamela, L., Díaz, M., y Tur, J., Nomograma para la determinación de viscosidad de jugos de caña., Tecnología Química, Vol. 19, No. 1, 1999, pp. 18-22.

Mendieta, O.A., y Escalante, H., Análisis experimental de la evaporación del jugo de caña de azúcar en película sobre una placa plana., Ciencia y Tecnología Agropecuaria, Vol. 14, No. 2, 2013, pp. 113-127.

Moncada, L., Diseño de plantas de procesos químicos. Intercambiadores de calor., Trujillo, Perú, Universidad Nacional de Trujillo, 2005, pp. 64-75. Disponible en: https://www.researchgate.net/file.PostFileLoader.html?id=551aa40bd3df3e4b098b4569&assetKey=AS:273746944823303@1442277766039

Reyes, M.B., Laureano, R.J., Pérez, S.R., y Nápoles, G., Aplicación del Método de la Colonia de Hormigas Mixto a la optimización de intercambiadores de calor de tubo y coraza., Revista Ingeniería Mecánica, Vol. 17, No. 2, 2014, pp. 129-137.

Segura, R., Heat Exchanger Design, Editorial Atlantic International University, Honolulu, 2012, pp. 71-93.

Torres, E., Quintana, L.E., Vega, O., y Retirado, Y., Coeficientes de transferencia de calor y pérdida de eficiencia en intercambiadores de calor de placas durante el enfriamiento del licor amoniacal., Revista Minería y Geología, Vol. 27, No. 2, 2011, pp. 67-83.

Recibido: 11 de Junio de 2018; Revisado: 05 de Julio de 2018; Aprobado: 09 de Agosto de 2018

^*Autor para la correspondencia: Isnel Benítez, Email: [e-mail]