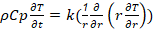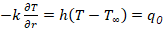INTRODUCCIÓN
La simulación y modelación de procesos, han sido utilizadas para regular tiempos y temperaturas durante las etapas de calentamiento y enfriamiento en procesos de pasteurización, cuando intervienen diferentes líquidos, entre ellos la cerveza, que se encuentran contenidos en varios tipos de recipientes. Se han obtenido perfiles de temperatura y velocidad de los fluidos, resultados de la cinética del proceso incluyendo el comportamiento de las unidades de pasteurización y se ha analizado en algunos casos la incidencia de la posición en la que se ubican los envases (Augusto et al., 2010; Laíce, 2013; Lespinard y Mascheroni, 2014).
El proceso de pasteurización cervecera se realiza en pasteurizadores de túnel, este producto se envasa la mayoría de las veces en botellas o latas, donde estas pasan por el interior del mismo siendo bañadas por el agua que se suministra a través de duchas. El equipo se divide fundamentalmente en tres zonas: precalentamiento, calentamiento y enfriamiento, (Mendieta et al., 2012).
Los estudios relacionados con la modelación matemática de la pasteurización de la cerveza envasada en botellas, han estado dirigidos a analizar el comportamiento del fluido. Se dice haber obtenido los mismos resultados, cuando el producto está contenido en las botellas que cuando se envasa en las latas, pero en ningún trabajo se ha encontrado el estudio realizado para el material del recipiente, es decir, no se ha considerado la velocidad de transferencia de calor, ni se hace un estudio de la distribución de temperatura en el sólido, ni el tiempo necesario. Lo toman como condiciones límites a través de la dinámica de fluidos computacional (Patiño et al., 2001; Hoffman, 2006).
Los envases utilizados para la cerveza son principalmente las latas de aluminio o botellas de vidrio. Estos materiales difieren en cuanto a su conductividad térmica, espesor y dimensiones geométricas. Las características de los recipientes tienen incidencia sobre los procesos de transferencia térmica que ocurren durante la pasteurización. Gracias a la transferencia de calor entre el agua rociada y el fluido contenido en el envase se genera un gradiente de temperatura en el seno de la cerveza, produciendo el movimiento relativo de las partículas y generando la convección natural. En general se evidencian tres mecanismos de transferencia de calor, convección forzada entre el agua rociada y la superficie externa del envase, conducción de calor a través de la pared del envase y convección libre entre la pared interna del envase y el fluido interno, es decir, dentro de la botella, donde se debe tomar en cuenta además, la difusión (Patiño et al., 2001).
Debido a la complejidad en la solución de las ecuaciones diferenciales fenomenológicas de cantidad de movimiento y calor, que se asocian a la pasteurización cervecera, es que se aplican los métodos finitos para resolver el problema, siendo la forma de resolver el sistema sin tener que construirlo físicamente. Se conocen entre estos, los métodos de diferencias finitas, volúmenes finitos y elementos finitos (MEF).
El método de diferencias finitas se basa en asignar puntos espaciados de manera apropiada sobre el dominio y aplicar las ecuaciones constitutivas correspondientes al fenómeno a cada punto, este método tiene como punto de partida las series de Taylor. El método de los volúmenes finitos se puede obtener de la ponderación de residuos con la función de pesos y aplicar el teorema de la divergencia de Gauss. Lo cual es equivalente a dividir el dominio en volúmenes de control y aplicar un balance de conservación a cada volumen. Por otra parte el MEF es un procedimiento numérico que se utiliza para resolver ecuaciones diferenciales sobre un dominio dado, en el cual el dominio es representado como una colección de dominios simples, denominados elementos finitos (Bosch, 2006; Toro, 2013).
En los últimos tiempos se han realizado simulaciones en procesos de pasteurización utilizando software profesionales que permiten obtener modelos multifísicos, es decir, relacionar la dinámica de los fluidos computacional con la transferencia de calor en sólidos. Esta situación es muy común, pues los alimentos fluidos pueden pasteurizarse, antes de ser envasados pero muchas veces se realiza este proceso cuando estos ya están contenidos en un recipiente. Entre los software se pueden mencionar el Ansys CFX, el cual basa la solución en el método de los volúmenes finitos y el COMSOL, el cual permite simular y modelar situaciones muy específicas, que se presentan en distintos procesos industriales, basando su análisis en el MEF (Hoffman, 2006; Lespinard y Mascheroni, 2014).
A partir de lo anterior, en este trabajo se tiene como objetivo realizar el estudio del calentamiento y enfriamiento del vidrio durante el proceso de pasteurización de la cerveza embotellada, utilizando el software COMSOL MULTIPHISICS v 5.1 para la simulación, basado en el método de los elementos finitos.
MATERIALES Y MÉTODOS
2.1. Descripción del sistema a modelar
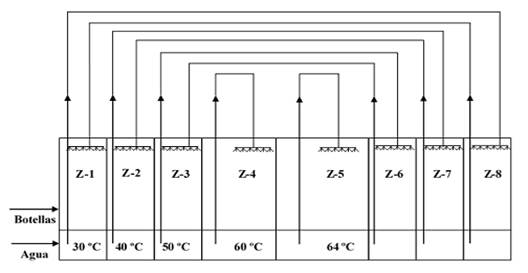
El sistema a modelar está formado por la botella que contiene la cerveza a pasteurizar y el agua que se suministra a través de las duchas dispuestas en el túnel de pasteurización para tal efecto. Esta transita por cada una de las zonas dentro del túnel, donde el agua que moja la botella por su cara exterior, posee temperaturas de 30, 40 y 50 ºC (303, 313 y 323 K), en las zonas 1 a 3 respectivamente, que son zonas de calentamiento. Estas aguas recirculan dentro del equipo con las zonas 8 a 6 que son de enfriamiento. La zona 4 es de pre-pasteurización y allí la temperatura del agua es de 60 ºC (333 K) y en la zona 5, donde ocurre la pasteurización, el agua tiene una temperatura de 64 ºC (337 K), estas dos zonas no recirculan. En la zona 5 la botella debe alcanzar la temperatura mínima de pasteurización que es de 60ºC (333 K), a esta temperatura se alcanza la letalidad de las bacterias según López (2010) y Pardo (2017).
La botella llega a la entrada del pasteurizador con una temperatura de 5ºC (278 K) y a partir de allí comienza el proceso de calentamiento paulatino hasta la pasteurización y luego el enfriamiento. Todo lo anterior puede observarse en la (Fig. 1), en la cual se presenta un esquema de un pasteurizador de túnel.
Como el objetivo del trabajo es estudiar los perfiles de temperatura que aparecen en el vidrio en función del tiempo, el dominio de simulación es representado por una botella de vidrio. Las dimensiones geométricas de esta son: 0,0286 m de radio interior, 0,239 m de altura y un espesor de 0,0027 m, se escogen estas características como ejemplo para este estudio, no respondiendo a ninguna en específico que se utilice en alguna industria.
Es necesario aclarar, que los envases que se emplean para la cerveza no tienen el mismo diámetro en toda su longitud o altura. Estos tienen un radio mayor en el fondo y a una altura determinada el radio se estrecha hasta el tope, pero el espesor del vidrio si es el mismo en todas la partes de la botella que están en contacto con la cerveza. Debido a lo anterior se ha considerado un radio único para toda la geometría que se estudia.
2.2. Modelo matemático del proceso estudiado
El modelo está formado por el balance de energía para el sólido en estado no estacionario obtenida de la simplificación de la ecuación general de balance térmico reportada por (Bird et al., 1979):
Con las condiciones iniciales y límites siguientes:
Condiciones iniciales:
Considerando que el vidrio se encuentra en equilibrio térmico con la cerveza:
Para el calentamiento:(a t = 0 s, T = 5 °C = 278 K)
Para el enfriamiento (a t = 0 s, T = 60 °C = 333 K)
Condiciones de contorno:
Estas condiciones son de tipo Newman según la ecuación (2), (Hoffman, 2006; Patiño et al., 2001).
En el fondo y en el tope del sistema se considera que el flujo de calor es nulo, comportándose como aislante térmico, ( 𝑞 0 =0).
En las paredes laterales las condiciones se expresan como un flux, siendo 𝑇 ∞ la temperatura del agua en cada zona
En la parte exterior del sistema es considerado un flujo de calor convectivo forzado, dado que el agua caliente, en cada zona, cae impulsada por bombas y a través de aspersores se distribuye uniformemente sobre las botellas. El coeficiente convectivo del agua, h, se evalúa mediante el software COMSOL MULTIPHISICS a partir de los criterios adimensionales Reynold (Re), Prandl (Pr) y Nusselt (Nu), los cuales están en función de las dimensiones de la botella y las propiedades termofísicas del agua (densidad, viscosidad dinámica, capacidad térmica específica y conductividad térmica) según las temperaturas dadas en el proceso.
El mecanismo de transferencia de calor que predomina en el sólido es la conducción del calor a través de un sólido, en estado no estacionario, en este caso se escogió como material Silica glass (vidrio de sílice). El software, ofrece sus propiedades termofísicas entre ellas la conductividad térmica (k), con un valor de 1,38 W/mK.
2.3. Procedimiento para el uso del software COMSOL v 5.1
Las simulaciones se llevan a cabo por un análisis de la combinación de la Dinámica de Fluidos Computacional, DFC, el cual se basa en el método de los elementos finitos. El modelo se obtiene para la geometría de la botella haciéndose un estudio del espesor hasta la parte fundamental que incluye el nivel de llenado de la cerveza similar a lo realizado por (Patiño et al., 2005). Debido a la simetría axial de las botellas en la posición vertical solo se considera la mitad de esta en la simulación.
RESULTADOS Y DISCUSIÓN
En la (Fig. 2), se puede observar como durante el calentamiento, en la botella ocurren cambios, se aprecia en 2a) a 2c) que desde el tiempo inicial hasta los 60 s, existe una variación de la temperatura desde 5 ºC (278 K) hasta 22 ºC (295 K), este último valor cercano a la temperatura del agua exterior que es de 30 ºC (303 K). Luego se puede observar en las (Fig. 2d) a (Fig. 2f) como a partir de los 90 s, ya se ve una homogeneidad de la temperatura y que a ese tiempo ya se ha alcanzado la estabilidad térmica. En el fondo de la botella debe haber intercambio térmico, pero este se ha despreciado, lo cual queda reflejado en la ecuación (1) donde se considera que la transferencia de calor es en el sentido radial. Esa es una de las suposiciones realizadas para la solución, esta parte está apoyada sobre la cinta transportadora.
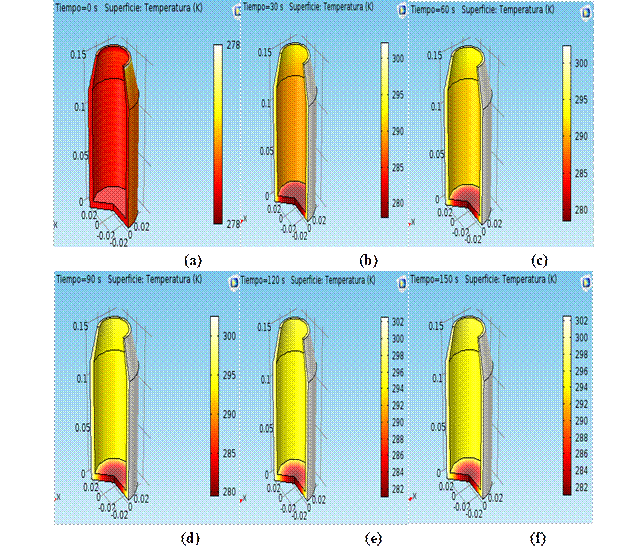
Fig. 2 Resultados del COMSOL durante el calentamiento a través del tiempo a) 0 s; b) 30 s; c) 60 s; d) 90 s; e)120 s; f) 150 s
Los datos que fueron obtenidos luego de la simulación del calentamiento de la superficie interna de la botella, hicieron posible construir la (Fig. 3), donde se observa el comportamiento de la temperatura interior de la botella en un tiempo de 70 s a partir del cual se logra estabilizar la temperatura, esta figura pertenece a la primera zona de calentamiento. Para el resto de las zonas de calentamiento, el tiempo es semejante. Pues, cuando la botella pasa de una zona a otra, recibe una nueva ducha de agua con una temperatura 10 grados mayor, siendo el mismo proceso en cada zona.
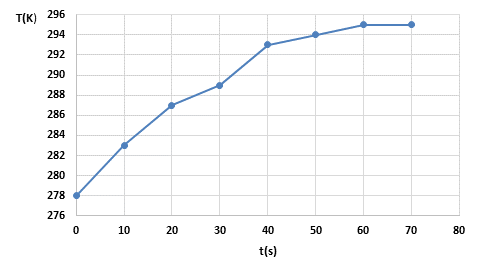
Fig. 3 Comportamiento de la temperatura interior de la botella en la primera zona, donde el agua está a una temperatura de 30 ºC (303 K)
La (Fig. 4a) a (Fig. 4f) muestra el resultado de la simulación del proceso de enfriamiento de la botella, desde una temperatura inicial de 60 ºC (333 K) encontrándose que en un tiempo de 120 s, se alcanza un color homogéneo en la superficie interior del envase.
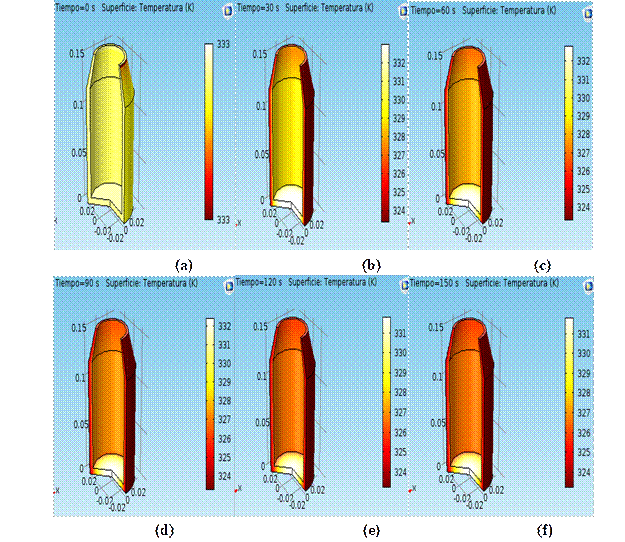
Fig. 4. Resultados del COMSOL durante el enfriamiento a través del tiempo. a) 0 s; b) 30 s; c) 60 s; d) 90 s; e)120 s; f) 150 s
De manera similar al proceso de calentamiento se tomaron los datos del enfriamiento, a partir de la simulación y se obtuvo la (Fig. 5), donde se puede ver el comportamiento de la temperatura del proceso en el tiempo, para la primera zona de enfriamiento y se observa que a partir de los 100 s, es que se estabiliza el proceso.
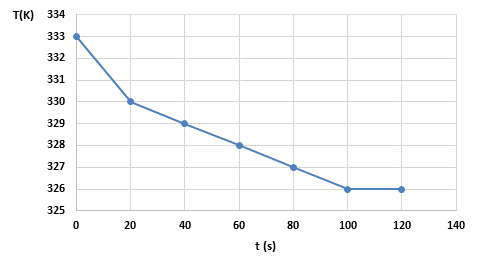
Fig. 5 Comportamiento del enfriamiento del vidrio en la zona 6, donde el agua está a una temperatura de 323 K
Como puede observarse el tiempo de enfriamiento es menor que el de calentamiento, esto se debe fundamentalmente a que las diferencias de temperatura son distintas (ΔT de calentamiento es de 25 ºC (K) y ΔT de enfriamiento 10 ºC (K)). Al ser menor la fuerza impulsora el proceso es más lento. Este resultado depende también de los fenómenos de dilatación y contracción que sufren los materiales cuando se someten a calentamientos y enfriamientos sucesivos, que provocan diferentes caminos, (Fernández, 1971).
Estas condiciones, se han tenido en cuenta adecuadamente en el diseño del funcionamiento del pasteurizador, el cual opera de manera satisfactoria. El hecho de que recircule el agua de las zonas 1, 2 y 3 con las zonas 8, 7 y 6 respectivamente, se debe a que durante las tres primeras zonas, el vidrio al calentarse progresivamente sufre tensiones térmicas. Estas se estabilizan en las zonas 4 y 5 donde se garantiza el tiempo suficiente de exposición, de 10 a 20 minutos, de la botella para que ocurra la pasteurización. Luego el enfriamiento debe ser lento para que el vidrio no reciba impactos térmicos bruscos, que influyan en la pérdida de la estabilidad de sus propiedades físicas y evitar así su rotura.
CONCLUSIONES
El estudio realizado acerca del efecto de la temperatura de pasteurización sobre la botella de cerveza, de acuerdo con las condiciones dadas, indica la necesidad de considerar un tiempo para este proceso tanto en el calentamiento como en el enfriamiento, los resultados encontrados han sido estudiados para un ejemplo, demostrando que no se debe omitir este tipo de análisis en procesos como estos:
Para el calentamiento es necesario un mínimo de 70 s, para que el vidrio alcance la temperatura del agua de riego, a partir de allí comenzaría el calentamiento de la cerveza.
Durante el enfriamiento de la botella, se observó una estabilidad térmica a los 100 s, por lo que puede considerarse suficiente para este proceso.
El uso de la simulación empleando el software COMSOL v 5.1, constituyó una herramienta importante para lograr el objetivo de esta investigación.