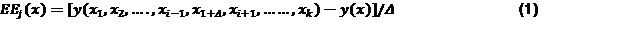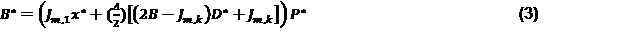Artículo original

Análisis de sensibilidad de los parámetros del modelo Pro-Alga para la simulación del crecimiento de Chlorella vulgaris

Sensitivity analysis of the PRO-ALGA model parameters for the growth simulation of Chlorella vulgaris

0000-0002-5438-325XOrlando Gines Alfaro-Vives^{1  *}  , 0000-0002-1464-3985Siannah María Más-Diego² 

¹ Centro de Investigaciones de Energía solar. Santiago de Cuba. Cuba

² Centro Nacional de Electromagnetismo Aplicado, Universidad de Oriente, Santiago de Cuba. Cuba

RESUMEN

•

El análisis de sensibilidad de un modelo matemático permite determinar cómo la incertidumbre de las salidas del modelo puede ser asignada a sus variables de entrada. En este trabajo se utiliza el método de Morris o de efectos elementales para realizar el análisis de sensibilidad global al modelo PRO-ALGA, para simulación del crecimiento de la microalga Chlorella vulgaris. Se siguieron los pasos siguientes: especificación de objetivos, selección de los factores a analizar, selección de las funciones de densidad de probabilidad para cada factor, generación de la muestra de entrada y evaluación del modelo. Los resultados permitieron identificar que los parámetros de entrada velocidad máxima de crecimiento de las microalgas (µ_a), constante de saturación media para el pH (K_pH), constante de saturación media para la concentración de algas (K_CA), coeficiente de transferencia de masa para el oxígeno a 25^oC durante el día (K_LAD) y coeficiente de transferencia de masa para el oxígeno a 25^oC durante la noche (K_LAN) son los que mayor influencia tienen sobre los parámetros de salida del modelo. El modelo es muy sensible a las variaciones de K_CA; los parámetros de entrada µ_a, K_LAD y K_LAN tienen efectos no lineales o de interacción sobre los parámetros de salida del modelo. Los parámetros de entrada K_pH y K_CA no tienen efectos significativos sobre las variables de salida.

Palabras-clave: efectos elementales; cultivo de microalgas; modelo matemático

•

ABSTRACT

•

The sensitivity analysis of a mathematical model allows to determine how the uncertainty of the model's outputs can be assigned to its input variables. In this work, the Morris or elemental effects method is used to perform the global sensitivity analysis to the PRO-ALGA model, to simulate the growth of the microalgae Chlorella vulgaris. The following steps were followed: specification of objectives, selection of the factors to be analyzed, selection of the probability density functions for each factor, generation of the input sample and evaluation of the model. The results allowed to identify that the input parameters maximum growth rate of microalgae (µa), mean saturation constant for pH (K_pH), mean saturation constant for algae concentration (K_CA), mass transfer coefficient for oxygen at 25 ºC during the day (K_LAD) and mass transfer coefficient for oxygen at 25 ºC at night (K_LAN) have the greatest influence on the output parameters of the model. The model is very sensitive to variations in K_CA; the input parameters µa, K_LAD and K_LAN have non-linear or interaction effects on the output parameters of the model. The input parameters k_pH and K_CA have no significant effect on the output variables.

Key words: elemental effects; microalgae cultivation; mathematical model

Introducción

Los modelos para crecimiento y desarrollo de cultivos autotróficos y mixotróficos de microalgas son necesarios para optimizar y controlar estos biosistemas. Una vez que se desarrolla un modelo mecanicista dinámico del crecimiento de microalgas, el análisis de sensibilidad estudia la determinación de la incertidumbre de las variables de salida a diferentes fuentes de incertidumbre de sus entradas.¹ En modelos dinámicos, los factores de entrada son las condiciones iniciales de las ecuaciones diferenciales, las variables de entrada y los parámetros.

El análisis de sensibilidad local calcula las derivadas parciales de las funciones de salida con respecto a las variables de entrada. Su principal limitante es que las derivadas parciales proporcionan información solamente del punto base donde son calculadas. ⁽² Además, cuando el modelo contiene funciones discontinuas, no pueden calcularse las derivadas. En estos casos puede emplearse el análisis con coeficientes de regresión estandarizados, gráficas de dispersión, prueba de efectos elementales (método de Morris), métodos basados en el cálculo de la varianza y filtrado de Monte Carlo.²

A diferencia de los métodos de análisis de sensibilidad local, los enfoques de sensibilidad global asignan la incertidumbre de la variable de salida a la incertidumbre de los factores de entrada, mediante el enfoque de muestreo de funciones de densidad de probabilidad (PDFs, por sus siglas en inglés) asociadas a las variables de entrada. En este caso, todos los parámetros se varían simultáneamente y las sensibilidades se calculan sobre el rango de variación completo de los factores de entrada.

Un enfoque muy usado para el análisis de sensibilidad en modelos mecanicistas que simulan el crecimiento de microalgas, es el método de Morris y simulación Monte Carlo.³ Los índices de sensibilidad global representan la contribución de cada factor de entrada (parámetro del modelo) a la varianza de la salida. Los índices de primer orden miden la influencia promedio de un factor sobre la salida del modelo sin tomar en cuenta los efectos de interacción para el factor analizado. Los índices totales calculan la suma de los índices factoriales que involucran al factor considerado.

Los análisis de sensibilidad global realizados a modelos de crecimiento de microalgas están bien limitados. En la literatura se realizó el análisis de sensibilidad global del modelo de crecimiento de microalgas BIO-ALGAE. ⁽¹⁾ Este modelo no tiene en cuenta la influencia del pH y la concentración de biomasa sobre la velocidad de crecimiento de las microalgas ni la influencia del consumo de bicarbonato y dióxido de carbono por las microalgas sobre la producción de oxígeno.

Por estas razones la hipótesis del presente estudio fue que un análisis de sensibilidad global, aplicado al modelo Pro-Alga para conocer el efecto de los parámetros del modelo matemático sobre las variables de salida, puede proporcionar mayor información que el análisis realizado al modelo BIO-ALGAE. Los objetivos del presente estudio fueron:

1) realizar el análisis de sensibilidad global utilizando el método de los efectos elementales o de Morris de un modelo de crecimiento autotrófico de la microalga Chlorella vulgaris cultivada en un fotobiorreactor de capa fina a cielo abierto, usando datos recolectados en el Centro de Investigaciones de Energía Solar, Santiago de Cuba;

2) Determinar los parámetros del modelo PRO- ALGA con mayor influencia sobre las variables de salidas del modelo y comparar los resultados obtenidos con los reportados para un análisis de sensibilidad global utilizando el método de efectos elementales al modelo BIO-ALGAE.

Materiales y métodos

El modelo Pro-Alga ⁴ para crecimiento de la microalga Chlorella vulgaris considera 7 procesos y 6 componentes y fue desarrollado en la plataforma MATLAB® / Simulink. MATLAB 2009.

Los procesos considerados son: crecimiento y absorción de las microalgas, procesos de descomposición y respiración de las microalgas, influencia de la variación de la temperatura, intensidad de luz y atenuación de la luz, pH, exceso de oxígeno disuelto, altas concentraciones de biomasa de microalgas y exceso de dióxido de carbono disuelto sobre la velocidad de crecimiento.

Se analiza el comportamiento de 6 componentes (5 solubles y 1 en partículas en suspensión), los componentes solubles son concentraciones de nitrógeno amoniacal (S_NH4), oxígeno (S_O2), ortofosfatos solubles (S_PO4) y dióxido de carbono (S_CO2), y el componente de partículas en suspensión es concentración de microalgas (X_ALG).

Metodología del análisis de sensibilidad global

El análisis de sensibilidad global considera los pasos siguientes.⁽¹⁾

Paso 1. Especificación de objetivos: los parámetros del modelo PRO- ALGA que tienen mayor o menor influencia sobre las variables de salidas del modelo.

Paso 2. Selección de los factores a analizar: los factores de entrada fueron los parámetros del modelo PRO-ALGA (tabla 1) y los factores de salida fueron las variables de salida del modelo: concentración de microalgas (X_ALG), concentración de carbono total disuelto (X_CT), concentración de nitrógeno amoniacal total disuelto (X_NT), concentración de Oxígeno disuelto (X_O2), y pH en la suspensión de cultivo.

Paso 3. Selección de las funciones de densidad de probabilidad (PDFs) para cada factor: como no se dispone de información adicional, se seleccionó una PDF uniforme para cada uno de los parámetros del modelo PRO-ALGA. Los intervalos inferior y superior para cada PDF (Tabla 1) se seleccionaron considerando 10 % de variación del parámetro alrededor de su valor nominal para ello se revisaron los trabajos realizados por.^1,5

Tabla 1 Parámetros del modelo Pro-Alga como factores de entrada para el análisis de sensibilidad global basado en el método de Morris 

Paso 4. Selección del método de análisis de sensibilidad: se empleó el método de los efectos elementales.⁶ Este método representa una estrategia de detección eficaz para identificar los factores más importantes en modelos altamente parametrizados.

Si se supone un modelo general, la salida del modelo y = y (x) es una función escalar de factores k-dimensionales (parámetros y valores de entrada) que constituyen un vector general x que identifica un punto exacto en el dominio experimental Ω del factor k-dimensional, que corresponde a un valor exacto de y. El vector x = {x₁, x₂… x_k} tiene k componentes, x _i . Cada una de estas puede tomar un nivel p en el conjunto {0, 1/(p -1), 2/(p-1), 3/(p-1),...,(p-2)/(p-1),…1}. Esto supone que el rango de cualquier factor k-dimensional se ha escalado a los niveles establecidos {0, 1/(p -1), 2/(p-1),…1}. La región de experimentación Ω es, por tanto, una cuadrícula de nivel p de dimensión k

Morris define el efecto elemental del i-ésimo parámetro de entrada a un valor dado de x ϵ Ω: ⁽⁷⁾

donde:

Δ es la magnitud de la longitud del paso que se puede asumir como valor en el conjunto {1/(p -1), 1- 1/(p-1)}, de modo que x + Δ todavía está en Ω.

Paso 5. Generación de la muestra de entrada: se construyó una orientación aleatoria 𝑟 en la región de experimentación, Ω constituida por p niveles.⁷ La magnitud del paso del experimento, Δ es un múltiplo de 1/(p -1). Se consideró p par y Δ = p/[2(p - 1)] para una construcción de diseño más económica. ⁷⁾ Se elige aleatoriamente un valor base x*, del vector x valores que van de 0 a 1- Δ, de modo que aumentando en Δ una de las k componentes, el vector x ⁽¹⁾ sigue en Ω. Se calcula el efecto elemental del i-ésimo componente de x ⁽¹⁾ por la ecuación (1), se seleccionan k + 1 nuevos puntos de muestreo de manera que dos puntos consecutivos difieran en un solo componente y se calcula el efecto elemental para cada factor. El vector creado x ⁽¹⁾ , x ⁽²⁾ ,…, x ^(k+1) define una trayectoria en el espacio de parámetros y una matriz de orientación B*.

donde:

J: Es (m.1) matriz unitaria,

D^*-Es una matriz diagonal k-dimensional en la que los elementos diagonales pueden tomar un valor de +1 de -1 con la misma probabilidad.⁷

P^*- Es una matriz k-dimensional donde cada columna y fila contiene solo un elemento igual a 1 y el resto a 0. La ubicación aleatoria de los 1 cambia el orden en que se perturban las variables, y aumenta el número de trayectorias.⁷⁾ Para determinar las direcciones aleatorias de la trayectoria se creó la matriz B^*:

donde:

^.

B - Es una matriz unitaria de triángulo inferior izquierdo aleatorio (m · k) con dos filas que difieren en un solo elemento;

La matriz de diseño X se construye cambiando el valor base x*, o las matrices seleccionadas al azar B, D* y P, r veces. El número total de simulaciones (𝑁) necesarias en el método de Morris es N = r · (k + 1).

Para garantizar una buena estimación de los índices de sensibilidad se generó, empleando el método de muestreo de Morris, una muestra de tamaño N(140, utilizando el programa para análisis de sensibilidad Simlab versión 2.2.

Paso 6. Evaluación del modelo. Índices del método de Morris: el efecto elemental sin escala EE_i,j arroja una clasificación incorrecta de los parámetros del modelo por lo que se determinaron los efectos elementales escalados SEE_i,j.⁸

donde: σ_i

σ_i y σ_y son las desviaciones estándar de los parámetros x _i y las salidas del modelo y _i . La distribución finita del SEE_i,j debido a la i-ésima variable de entrada en la j-ésimo salida del modelo se denota como F _i,j .

La media y la desviación estándar del método propuesto ⁷ indican el impacto del i-ésimo factor de entrada sobre la salida j-ésima y la dependencia de su sensibilidad con los valores de otros parámetros. ⁸⁾ Una media alta, µ indica un parámetro con un efecto general importante en la salida. Una desviación estándar alta, σ indica un parámetro con un efecto no lineal en la salida o que interactúa con otros parámetros. Cuando la distribución F _i,j no es monótona se emplea μ modificado, μ*.⁶

Basado en μ _i ^* y σ_i, se identifican los factores con efectos insignificantes, lineales y aditivos, o no lineales o efectos de interacciones.⁸ La figura 1 ilustra esta interpretación.

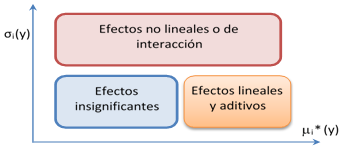
Fig. 1 Representación esquemática de la disposición teórica de las medias • µ • 𝑖 • ∗ • y las desviaciones estándar • ?? • 𝑖 • de la distribución de efectos. (Adaptado de ⁸) 

Con estas medidas de sensibilidad se identificaron los parámetros más influyentes.⁷ Los valores de μ _i,j y σ_i,j obtenidos para las distribuciones F_i,j se muestran junto con dos líneas correspondiente a 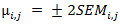, donde 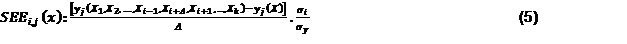es el error estándar de la media que se puede estimar como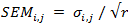. Los parámetros que se encuentran dentro de la "cuña" creada por las dos líneas se consideran no influyentes o insignificantes. Los parámetros que se encuentran fuera de la cuña tienen un efecto significativo.^7,8

El modelo PRO-ALGA ⁴ se programó en el ambiente Matlab-Simulink (Mathworks Inc., 2009). Usando una muestra de tamaño 140, para los factores de entrada (parámetros), se ejecutaron las simulaciones correspondientes y se almacenaron los valores de las variables de salida del modelo concentración de microalgas (X_ALG), concentración de carbono total disuelto (X_CT), concentración de nitrógeno amoniacal total disuelto (X_NT), concentración de Oxígeno disuelto (X_O2) y pH en la suspensión de cultivo. Se desarrolló un programa en Excel para estos cálculos.

Resultados y discusión

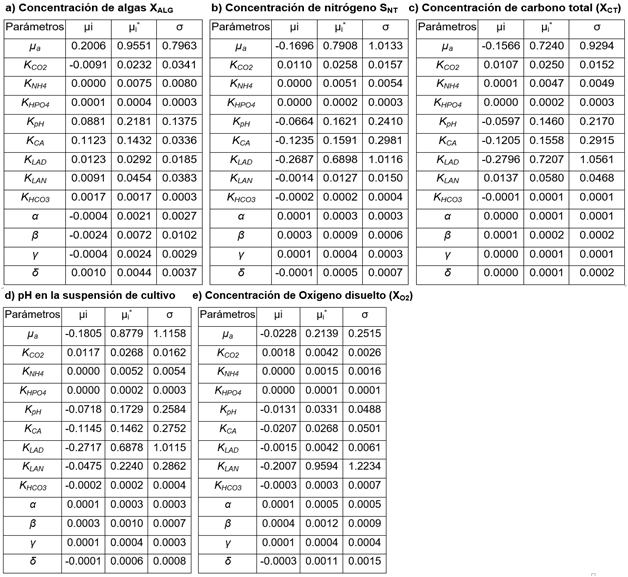
Los resultados del método de Morris se evaluaron comparando las medias y las desviaciones estándar de la función F_i,j para cada entrada. La tabla 2 muestra las medidas de sensibilidad resultantes de los parámetros de entrada µ_a, K_CO2, K_NH4, K_HPO4, K_pH, K_CA, K_LAD, K_LAN, K_HCO3, α, β, γ, δ para cada variable de salida analizada en r=10.

La figura 2 muestra los gráficos de barras de los módulos las medidas del efecto medio (µ_i ^*) de la distribución de los parámetros de entrada en la salida del modelo.

La media y la desviación estándar de los 13 parámetros de entrada fueron graficados en la figura 3 para las 5 variables de salidas consideradas (X_ALG, S_NT, S_CT, pH, S_O2).

La figura 4 incluye las medidas del efecto medio μ _i,j ^* y las desviaciones estándar σ _i,,j

de la distribución de los parámetros de entrada en la salida del modelo e ilustra los efectos lineales y aditivos y los no lineales o de interacción.

Tabla 2 Medidas de sensibilidad del parámetro de entrada (r=10) para cada variable de salida 

Fig. 2 Medidas del efecto medio, µ_i ^*, de los parámetros de salida con respecto a cada entrada del modelo a) X_ALG, b) S_NT, c) S_CT, d) S_pH, e) S_O2 

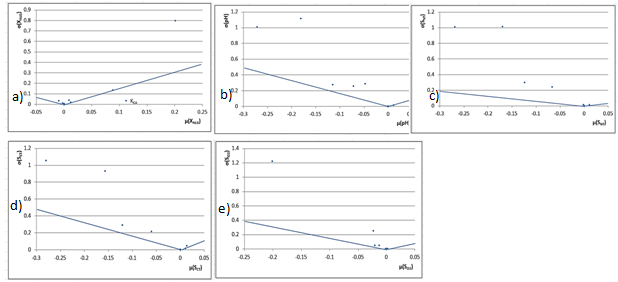
Fig. 3  Medidas de sensibilidad de la distribución de los efectos elementales de las entradas a) X_ALG, b) S_NT, c) S_CT, d) S_pH, e) S_O2 sobre las salidas del modelo 

Fig. 4 Medidas de la sensibilidad µ_i ^* _i,j versus σ_i,j para las salidas del modelos a) X_ALG, b) S_NT, c) S_CT, d) S_pH, e) S_O2 

La media de los efectos elementales escalados se muestra en la figura 2a. Esta permite identificar los parámetros de entrada µ_a, K_pH, K_CA y K_LAD como los que mayor influencia tienen sobre la concentración final de algas (X_ALG).

Los parámetros de entrada µ_a, K_pH y K_LAD en la figura 3a están dentro de la cuña formada por • 𝜇 • 𝑖,𝑗 • = • − • + • • 2𝑆𝐸𝑀 • 𝑖,𝑗 • • lo que indica que el modelo no es sensible a variaciones de estos parámetros. Sin embargo, el modelo es sensible a las variaciones de K_CA, lo que resulta lógico pues variaciones tan pequeñas de µ_a, K_pH y K_LAD provocan cambios muy pequeños en la variable de salida, sin embargo, altas concentraciones iniciales de microorganismos reducen la producción de biomasa.

En la figura 4a se identifica el parámetro de entrada µ_a con efectos no lineales o de interacción con respecto a la variable de salida X_ALG. Los demás parámetros tienen efectos no significativos sobre la salida X_ALG. Sin embargo, para optimizar los parámetros del modelo resultaría interesante estudiar las alteraciones que pueden producir los cuatro parámetros µ_a, K_pH, K_CA y K_LAD sobre la salida X_ALG del modelo.

En las figuras 2b, 2c y 2d se observa que la media de los efectos elementales escalados permite identificar a los parámetros de entrada µ_a, K_pH, K_CA y K_LAD como los que mayor influencia tienen sobre la concentración final de nitrógeno amoniacal (S_NT), la concentración de carbono total (S_CT) y el pH.

En las figuras 4b, 4c y 4d se observa que los parámetros de entrada µ_a y K_LAD tienen efectos no lineales o de interacción con respecto a las variables de salida S_NT, S_NT y pH. Es importante señalar que estas salidas de simulación fueron sensibles al pH, que a su vez fue influenciado por la velocidad de crecimiento de las microalgas y por el coeficiente de transferencia de masa de los gases a la atmósfera (µ_a y K_LAD) parámetros que tienen efectos no lineales o de interacción con el pH.

En la figura 2e se puede observar que la media de los efectos elementales escalados permite identificar los parámetros de entrada µ_a y K_LAN como los que mayor influencia tienen sobre la concentración final de oxígeno (S_O2). Por tanto, si se pretende optimizar los parámetros del modelo, es necesario tener en cuenta para el análisis a µ_a, K_pH, K_CA, K_LAD y K_LAN que son los parámetros con mayor influencia sobre los parámetros de salida.⁷

Durante la noche la concentración de oxígeno está influenciada por el consumo de oxígeno por la respiración endógena de los microorganismos y por el intercambio de gases con la atmósfera que a su vez depende de la temperatura de la suspensión de cultivo en el modelo. Este comportamiento se refleja en la figura 4e, donde se identifica el parámetro de entrada K_LAN con efectos no lineales o de interacción con respecto a la variable de salida (X_O2).

Resulta difícil comparar los resultados obtenidos por ¹ con los alcanzados en este trabajo pues la desviación estándar de los parámetros de entrada no fue modificada en la misma escala y esto afecta el valor final de los índices del método de Morris, pero este análisis identifica los mismos parámetros de entradas como los más importantes µ_a, K_LAD y K_LAN. Existen parámetros en el modelo PRO-ALGA que no son identificados en el trabajo de ⁽¹⁾ como K_CA que resultó ser el parámetro al que el modelo es más sensible y K_pH que tiene influencia sobre las variables de salida del modelo X_ALG, S_NT, S_CT y pH.

Conclusiones

1. Los parámetros µ_a, K_pH, K_CA, K_LAD y K_LAN son los que mayor influencia tienen sobre los parámetros de salida del modelo X_ALG, S_NT, S_CT y pH. El parámetro de entrada µ_a tiene efectos no lineales o de interacción sobre X_ALG, S_NT, S_CT y pH del modelo. K_LAD tiene efectos no lineales o de interacción sobre S_NT, S_CT y el pH.

2. Los parámetros de entrada que mayor influencia tienen sobre la concentración de oxígeno (S_O2) son µ_a y K_LAN. Ambos tienen efectos no lineales o de interacción sobre S_O2.

3. El modelo PRO-ALGA es muy sensible a las variaciones de la constante de saturación media para la concentración de algas (K_CA).

4. Los parámetros de entrada µ_a, K_LAD y K_LAN son los de influencia más significativa para ambos modelos PRO-ALGA y BIO-ALGAE. En el modelo PRO-ALGA existen parámetros nuevos que no existen en BIO-ALGAE tales como K_CA que resultó ser el parámetro al que el modelo es más sensible y K_pH que tiene influencia sobre las variables de salida del modelo X_ALG, S_NT, S_CT y pH.

Nomenclatura

K_CA: constante de saturación media para la concentración de algas

K_LA,CO2: coeficiente de transferencia de masa para el dióxido de carbono a 25^oC

K_LA,NH3: coeficiente de transferencia de masa para el amoniaco a 25 ^oC

K_LA,O2: coeficiente de transferencia de masa para el oxígeno a 25 ^oC

K_LAD: coeficiente de transferencia de masa para el oxígeno a 25^oC durante el día

K_LAN: coeficiente de transferencia de masa para el oxígeno a 25^oC durante la noche

K_pH: constante de saturación media para el pH

PDF: función de densidad de probabilidad

S_CO2: concentración de dióxido de carbono

SEM _i,j : error estándar de la media SEM _i,j

S_NH4: concentración de nitrógeno amoniacal

S_O2: concentración de oxígeno

S_PO4: concentración de ortofosfatos solubles

X_ALG: concentración de algas

X_CT: concentración de carbono total disuelto

X_NT: concentración de nitrógeno amoniacal total disuelto

X_O2: concentración de Oxígeno disuelto

µ_a: velocidad máxima de crecimiento de las microalgas

µ_i ^*: medidas del efecto medio de la distribución de los parámetros de entrada en la salida del modelo

σ _i,j : desviaciones estándar de la distribución de los parámetros de entrada en la salida del modelo

Referencias bibliográficas

1.  SOLIMENO, A.; SAMSÓ, R.; GARCÍA, J. Parameter sensitivity analysis of a mechanistic model to simulate microalgae growth. Algal Research. 2016, 15, 217-223. ISSN: 2211-9264.

2.  SALTELLI, A., et al. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Computer Physics Communications. 2010, 181 (2), 259-270. ISSN: 0010-4655.

3.  MAKOWSKI, D., et al. Global sensitivity analysis for calculating the contribution of genetic parameters to the variance of crop model prediction. Reliability Engineering & System Safety. 2006, 91 (10), 1142-1147. ISSN: 0951-8320.

4.  ALFARO, O. , et al. Producción de biofertilizantes a partir de la biomasa de microalgas. En: Proyecto Interno. Comunicación personal. Santiago de Cuba: Centro de Investigaciones de Energía Solar, 2019.

5.  SOLIMENO, A.; PARKER, L.; LUNDQUIST, T. ; GARCÍA, J. Integral microalgae-bacteria model (BIO_ALGAE): Application to wastewater high rate algal ponds. Science of The Total Environment. 2017, 601-602, 646-657. ISSN: 0048-9697.

6.  CAMPOLONGO, F.; SALTELLI, A. ; CARIBONI, J. From screening to quantitative sensitivity analysis. A unified approach. Computer Physics Communications. 2011, 182 (4), 978-988. ISSN: 0010-4655.

7.  MORRIS, M. D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics. 1991, 33 (2), 161-174. ISSN: 0040-1706.

8.  SIN, G. ; GERNAEY, K. V. "Improving the Morris method for sensitivity analysis by scaling the elementary effects." En: JEŻOWSKI, J. ; THULLIE, J. eds. Computer Aided Chemical Engineering. Elsevier, 2009, vol. 26, p. 925-930. ISBN 1570-7946.

Recibido: 08 de Agosto de 2021; Aprobado: 15 de Diciembre de 2021

^*Autor para la correspondencia: correo electrónico: [e-mail]

Los autores declaran que no existe conflicto de intereses.

Orlando Gines Alfaro Vives: toma de muestras, realización de cálculos y preparación del modelo, procesamiento de datos, elaboración de programas y escritura del artículo.

Siannah María Más Diego: elaboración de programas y revisión del artículo.