INTRODUCCIÓN
Una de las razones para estudiar las enfermedades infecciosas es incrementar el control y erradicación de las mismas. Los modelos matemáticos pueden ser una herramienta poderosa para este fin permitiendo optimizar los recursos limitados y dirigir medidas más efectivas, estos modelos se hacen para la predicción y para aumentar la comprensión del fenómeno en estudio. Estos deben ser tan simples como sea posible y a la vez precisos, flexibles y trasparentes (Vidal et al., 2020).
La Epizootiología en su esquema metodológico tradicional, al igual que otras tantas disciplinas; ha tenido un enfoque basado en la mecánica de Descartes y Newton, por lo que en muchas ocasiones mantiene el esquema tradicional de causa efecto basado en modelos de ecuaciones lineales, donde todo funciona como una maquinaria de forma predecible (Ivorra et al., 2020).
Las epidemias y epizootias con sistemas complejos adaptativos. El sello distintivo de los sistemas complejos es su comportamiento de interacción no lineal e impredecible. Estos están estructurados como un gran número de elementos interactuando entre sí, cuyas repetidas interacciones resultan en un comportamiento colectivo que retroalimenta al comportamiento de las partes individuales (Caparrini et al., 2016; Soler, 2017) que se pueden capturar en modelos matemáticos.
Con el valor de R0 se determina cuando un agente patógeno puede invadir o persistir en una población susceptible sin inmunidad. Los agentes patógenos pueden evolucionar aumentando R0. Este valor es un indicador válido para medir la efectividad de las medidas de control que se requieren para eliminar las epidemias, cuando R0=1 ó R0 <1 no hay epidemias (Vidal et al., 2020; Ridenhour, Kowalik y Shay, 2015).
La dinámica actual conlleva a aplicar teorías transdisciplinarias, por tanto, las universidades tienen el reto de liderar el proceso de transformación, introduciendo cambios en los procesos formativos que permitan a los futuros profesionales en salud pública, encontrar en la transdisciplinariedad, una herramienta para fortalecer la investigación y el diálogo de saberes (Castilla, Guerra y Villadiego, 2018).
Se manifiestan cambios en el uso de la Inteligencia Artificial, nuevas maneras de aprendizaje a distancia, consultas médicas a distancia y otros, lo que demuestra que para lograr resiliencia hay que fortalecerse en estos métodos adaptativos que requieren enfoques integradores (Martins, 2020).
Son pocas las enfermedades de las personas sin un vínculo a circulación animal (influenza, tripanosomiasis y una extensa lista de zoonosis), esta dinámica compleja se puede recoger en modelos matemáticos vitales para las políticas de control sanitario (Lloyd-Smith et al., 2009).
En general la simulación (Ortiz, Vázquez y Aguilar, 2020) permite estudiar un sistema sin tener que realizar experimentación sobre el real y efectuar experimentos de muestreo sobre el modelo de un sistema. Un modelo no es más que un conjunto de variables junto con ecuaciones matemáticas que las relacionan. Los experimentos reales son de alto costo, lentos, sus pruebas a veces son destructivas y con violaciones de la ética médica. El presente trabajo tiene como objetivo realizar simulaciones con el modelo estocástico Susceptible, Infectado, Recuperado (SIR) para introducirlos en la docencia, en los análisis epizootiológicos y en la toma de decisiones.
MATERIALES Y MÉTODOS
El modelo básico SIR (Susceptibles-Infectados-Recuperados) de Kermack y McKendrick, es un modelo de compartimentos donde la población bajo estudio se divide en clases epidemiológicas y se describe un flujo entre ellas (Vidal, 2020; Manlove et al., 2019).
En este tipo de modelos matemáticos, el número reproductivo básico, (R0) refleja la media del número de casos secundarios que provocará un enfermo primario en la población que no tiene previa inmunidad. Para determinar el número reproductivo (R0) se utiliza el modelo siguiente:
R0= β So (1/ γ)
Donde:
β = índice de transmisibilidad
So= Susceptibles sin inmunidad al inicio
γ= duración de la enfermedad
β So es el número de nuevos casos que surgen (incidencia)
1/ γ es el promedio de duración de la infección
Se simuló un modelo estocástico (Rincón, 2012) con el paquete EpiModel presente en el programa R (R_Core_Team, 2021) la entrada de diez aves migratorias enfermas de procesos respiratorios en fincas de criadores de aves donde hay como promedio un total de 5000 aves de corral de diferentes tipos. Se determinó el R0 (paquete RO, programa R) de acuerdo a la incidencia.
RESULTADOS
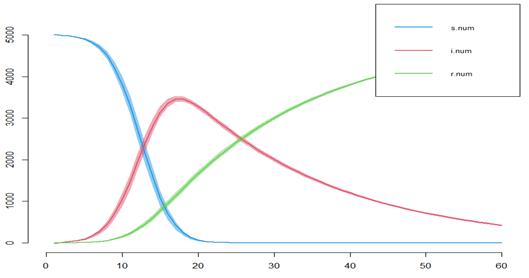
La simulación (Fig. 1) se corrió con un índice de transmisibilidad bajo (1,8 %), es decir, se enferman 1,8 de cada 100 y cada ave contacta un promedio de cinco aves de manera aleatoria durante 10 días. De no hacer ninguna intervención habría a los 20 días un pico de enfermos que sobrepasaría los 3000.
Se encontró un número reproductivo básico mayor que la unidad (R0=1,14) por lo que califica como brote epidémico (Ke, Romero-Severson, Sanche y Hengartner, 2021).
DISCUSIÓN
De manera sostenible, un profesional de la salud animal o pública puede valorar lo que se avecina, de hecho, debe diagnosticar y resolver el problema en los primeros 10 días, pues el crecimiento exponencial de la incidencia llegaría a sobrepasar los 3000 casos antes de los 20 días. Cada enfermo primario es capaz de infectar a 1,14 aves. No es conveniente esperar una inmunidad del rebaño (Trincado, 2020).
Se han estudiado patrones de dispersión de enfermedades respiratorias en personas y se han relacionado al mundo animal doméstico y silvestre (Torres et al., 2020). En el caso de las aves migratorias, con su gran capacidad de desplazamiento, estas pueden contraer y dispersar infecciones por agentes patógenos peligrosos para los humanos (como el virus de la influenza aviar altamente patógena, el virus del Nilo Occidental, Chlamydia psittaci, entre otros), especialmente en el caso de las aves migratorias (Contreras et al., 2016; Sánchez et al., 2020).
Las aves acuáticas silvestres representan el principal reservorio natural de los virus influenza y han participado en el reordenamiento tanto de virus pandémicos como de los virus responsables de los brotes de gripe aviar en las especies domésticas y silvestres (Sánchez et al., 2020).
Las personas tienden a crear vínculos afectivos con los animales, incluyendo a las aves, sin tener percepción del riesgo a que se exponen. Con frecuencia las aves viven en patios e interiores de las casas, sin mantener el distanciamiento necesario y en ocasiones son acariciadas. Este comportamiento social influye entre otros factores en la posibilidad de contagio de los seres humanos (Gibb et al., 2020)
En entrenamientos de las matemáticas en Moodle se observó el desarrollo de competencias cooperativas así como también el auto-reconocimiento de deficiencias en la compresión de algunos conceptos por los alumnos (Perera et al., 2020).
La educación a distancia por su parte tiene una rápida expansión en los sistemas universitarios a nivel internacional por las ventajas que presenta, y de modo particular a través del uso de las tecnologías de la información y las comunicaciones (TIC), en las que por medio del empleo de entornos virtuales se puede acceder a un curso desde cualquier lugar, basta con estar conectado a redes informáticas (Céspedes et al., 2016). Se requiere un cambio metodológico que permita transitar de un método centrado en el contenido y el profesor, a uno centrado en las e-actividades y el alumno (Quiroz-Silva, 2017).
El veterinario de campo necesita un estilo de educación transdisciplinaria que incluya de manera sistemática estos modelos matemáticos para resolver diferentes problemas que se presentan en la vida real, por lo que se impone realizar un cambio organizacional en el que se modifiquen estilos de trabajo y formas auto-organizativas de la actividad (Cárdenas y Estrada, 2021; Belcher et al., 2016).
CONCLUSIONES
Se realizaron simulaciones con el modelo estocástico con una herramienta analítica sustentable basada en el programa libre R.
Se constató la necesidad de integrar la epizootiología, la epidemiologia y la matemática; por lo que deben entrenarse en estos aspectos a los estudiantes relacionados con la salud animal y la salud pública.
Se expone la conveniencia de sistematizar entrenamientos de modelos matemáticos en la educación presencial y a distancia