ARTÍCULO ORIGINAL

 

Algoritmo paralelo en memoria compartida para el cálculo de la pendiente del terreno usando OpenMP

 

Shared memory parallel algorithm for extracting the terrain slope using OpenMP

 

 

Grethell Castillo Reyes^1*,Liesner Acevedo Martínez¹, Guillermo Luzua Farias¹

¹Universidad de las Ciencias Informáticas. Carretera a San Antonio de los Baños, km 2 ½, Torrens, La Lisa, La Habana, CP. 19370.

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

Los Modelos Digitales de Elevación son la base para el cálculo de varios parámetros de caracterización de la topografía del terreno, tales como la pendiente. El cálculo de estos parámetros es importante para los Sistemas de Información Geográfica, debido a que sus aplicaciones tienen impacto directo en la toma de decisiones a la hora de evaluar las características del terreno en situaciones de emergencia, por ejemplo: posibles inundaciones y deslizamientos de tierra en las laderas montañosas. La mayoría de los algoritmos utilizados para su cálculo son complejos desde un punto de vista computacional y dependen del tamaño y la resolución de los MDE. Uno de los principales retos en este sentido consiste en el diseño e implementación de algoritmos paralelos que utilicen todo el potencial de procesamiento de las computadoras modernas con el fin de reducir el tiempo de cálculo. La principal contribución de este trabajo es la propuesta de un algoritmo paralelo de memoria compartida que utiliza las capacidades de computación de los procesadores multinúcleos. La propuesta se llevó a cabo utilizando la interfaz de programación de aplicaciones OpenMP. Los experimentos llevados a cabo muestran un buen rendimiento general.

Palabras clave: Modelo Digital de Elevación, pendiente, procesamiento paralelo

---

ABSTRACT

The Digital Elevation Models are the basis to calculate several terrain parameters to characterize topography, such as the slope. The calculation of this parameters is important for the Geographic Information Systems, because their applications have direct impact on decision making when it comes to assess the terrain characteristics in emergency situations, for example: possible floods and landslides in mountainous slopes. Most of the algorithms used are complex from a computational point of view and depend on the size and resolution of the DEMs. One of the main challenges in this regard involves the design and implementation of parallel algorithms that use the full potential of modern computer processing in order to reduce the computation time. The main contribution of this paper is the proposal of a shared memory parallel algorithm that uses computing capabilities of multicore processors. The proposal was implemented using the Application Programming Interface OpenMP. The experiments carried out show a good overall performance.

Key words: Digital Elevation Model, parallel processing, slope, OpenMP

---

 

 

INTRODUCCIÓN

Los Modelos Digitales de Elevación (MDE) representan la elevación del terreno sobre un nivel base, obtenida generalmente usando técnicas de teledetección o LIDAR. Su estructura constituye normalmente una matriz bidimensional A con n filas m columnas, que conforman nxm celdas, donde Cada celda con representa un valor numérico que toma valores en R y que describe la elevación del terreno en ese punto (Martínez, 2011).

Este modelo es la base para un gran número de algoritmos de análisis de superficies, que permiten calcular y modelar parámetros propios del terreno para caracterizar la topografía, como es el caso de la pendiente. Este atributo, no solo contribuye de manera general a las ramas que engloban el tratamiento y análisis de la información geográfica, sino que, además, diversos modelos ambientales dependen en gran medida de su resultado. Es empleado en un conjunto de estudios para el análisis de la inclinación de superficies, determinación de zonas de poca pendiente favorables para la construcción (Rodríguez and Suárez 2010) o zonas de mucha pendiente que determinan erosión o deslizamientos de tierra (Biesemans et al. 2000). Permiten además generar mapas de sombra para percibir la profundidad de una superficie en tres dimensiones (Bernhard, 2001) y determinar la variabilidad de un relieve en un entorno determinado (Seitavuopio et al. 2005).

Investigaciones realizadas (Nikolakopoulos et al. 2006; Frau et al. 2011) demuestran que con los avances tecnológicos, la disponibilidad de datos de la superficie del terreno ha ido en aumento sostenido y cada vez con un mayor nivel de resolución espacial y precisión. Como resultado, la memoria requerida para el almacenamiento de los MDE generados es cada vez mayor. Además, el cálculo para la extracción de los parámetros del terreno se hace cada vez más costoso a través de los algoritmos secuenciales (Jiang et al. 2013). Aunque se han propuesto diversos enfoques matemáticos (Rodríguez and Suárez 2010), su complejidad temporal continua siendo con respecto al origen de datos.

Teniendo en cuenta esto, varios autores, se enfocan en la utilización de sistemas distribuidos para reducir el tiempo de ejecución de los algoritmos para el cálculo de la pendiente, empleando la Interfaz de Paso de Mensajes (MPI) (Zhan and Qin 2012; Qin et al. 2014b). Las soluciones propuestas son eficientes respecto a las variantes secuenciales, sin embargo, requieren que se cuente con una infraestructura de cálculo dedicada a ese fin (ejemplo: un clúster o multiprocesador). Por otro lado, con la llamada “Revolución Multinúcleo” (Herlihy, 2007) las computadoras personales cuentan con arquitecturas paralelas que, bien aprovechadas, pueden usarse para la ejecución de tareas en paralelo y obtener mejores tiempos de respuesta para las aplicaciones.

En el presente trabajo se exponen los principales enfoques matemáticos para la obtención de la pendiente del terreno. Se propone un algoritmo para su cálculo paralelo empleando la técnica de programación OpenMP y se realiza un análisis comparativo con el algoritmo secuencial empleado para su cálculo. Además, se valoran parámetros como la ganancia de velocidad y la eficiencia del algoritmo paralelo.

Cálculo de la pendiente

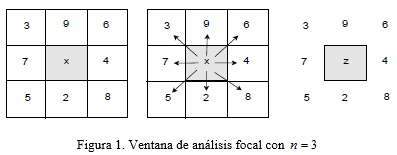
Dentro del álgebra de mapas, las funciones para el análisis del terreno a partir de la extracción de sus parámetros son clasificadas como funciones de análisis focal o de vecindad, en relación con la distribución de las celdas que se utilizan para obtener un resultado. Esto se debe a que el valor de una celda se obtiene a partir de su propio valor y teniendo en cuenta el valor de sus vecinos más próximos, definiendo una matriz de recorrido de tamaño nxn  alrededor de la celda analizada, como se muestra en la Figura 1. Las funciones más habituales emplean matrices con n=3. Posteriormente, esta matriz se utiliza para obtener el valor de ese punto en el terreno derivado de la aplicación de un algoritmo de análisis espacial.

La pendiente es una de las características que se define en la literatura como parámetro primario del terreno, debido a que constituye el punto de partida para la realización de otros análisis basados en la obtención de parámetros más complejos derivados de este y que permiten aportar mayor información sobre las características del relieve en un entorno determinado (Serrano et al. 1998) . Existen varios enfoques matemáticos para su cálculo (Fleming and Hoffer 1979; Horn, 1981; Zevenbergen and Thorne 1987), sin embargo, estudios realizados (Rodríguez and Suárez 2010; Zhou and Liu 2004) arrojan como conclusión que los más apropiados son el método de Diferencia Finita de segundo grado (Zevenbergen and Thorne 1987) y el método de Diferencia Finita de tercer grado (Horn, 1981).

Dado un punto a_ij del terreno, la pendiente P(a_ij) se calcula como sigue:

Donde g_x y g_y corresponden a las funciones del gradiente Este – Oeste y Norte - Sur respectivamente. Estas funciones son calculadas a partir de la matriz de recorrido (ecuación 2) correspondiente al punto a_ij expresado en la siguiente ecuación:

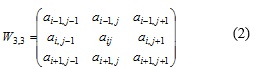
Según el método de Diferencia Finita de segundo grado definido en (Zevenbergen and Thorne 1987), g_x y g_y se expresan según las siguientes ecuaciones:

Según el método de Diferencia Finita de tercer grado definido en (Horn 1981), g_x se calcula como sigue:

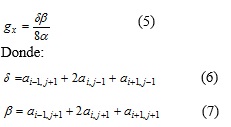
Y g_y se calcula como sigue:

Análisis del algoritmo secuencial

Teniendo en cuenta la descripción anterior, siendo f el MDE a procesar, la matriz asociada, donde es la pendiente del terreno en a_ij , el flujo secuencial de las operaciones realizadas por el algoritmo para el cálculo de la pendiente del terreno se describe en el Algoritmo 1.

La primera operación que se ejecuta es la lectura de los metadatos del dataset raster a procesar. A partir de estos metadatos se crea el dataset de salida.

Una vez realizadas las operaciones anteriores, para cada fila i de la matriz A se realiza la lectura de los datos y para cada celda a_ij de A se ejecutan dos operaciones esenciales: se crea la matriz de vecindad W con n = 3 (líneas 7 – 16 del Algoritmo 1) y en cada iteración W se emplea para obtener la pendiente del punto a_ij calculando los gradientes correspondientes a partir de las celdas vecinas, mediante los enfoques matemáticos propuestos en (Horn, 1981) y (Zevenbergen and Thorne 1987) (línea 17 del Algoritmo 1). Estos resultados se van almacenando en el buffer A' hasta que finalice la iteración, para luego ser escritos en el archivo de salida O (línea 19 del Algoritmo 1).

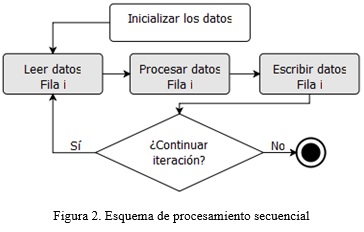
A los efectos de este trabajo, esta secuencia de operaciones es la más relevante. Precisamente, esto se debe a que independientemente del tamaño de la estructura a analizar, el procesamiento de los datos se realiza fila por fila, como se ilustra en el esquema de la Figura 2.

Desde el punto de vista algorítmico, las operaciones relacionadas con la inicialización de los datos son consideradas operaciones elementales de orden O(1), por lo que no influyen significativamente en el tiempo de procesamiento de los algoritmos. Sin embargo, teniendo en cuenta que la matriz de entrada A tiene n filas y m columnas y que se itera por cada fila i y columna j, desplazando la matriz de vecindad por cada celda para realizar los cálculos correspondientes, entonces la complejidad temporal del algoritmo está dada por la ecuación:

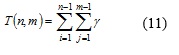
Siendo un valor constante que representa la cantidad de operaciones elementales ejecutadas en cada iteración. Aplicando la definición de cota superior, se deduce que por lo que la complejidad temporal de los algoritmos es de orden (n * m).

Estrategia de paralelización

Descomposición de dominio

Como plantean los autores en (Guan and Clarke 2010), (Barnes et al. 2011), desde la perspectiva de computación, el procesamiento de datos raster puede ser paralelizado, dado que la estructura matricial utilizada para su almacenamiento puede ser particionada en varias submatrices y asignadas a múltiples procesadores para su cómputo. Este proceso es conocido como descomposición de dominios, y se considera un elemento fundamental en el procesamiento de datos raster en paralelo.

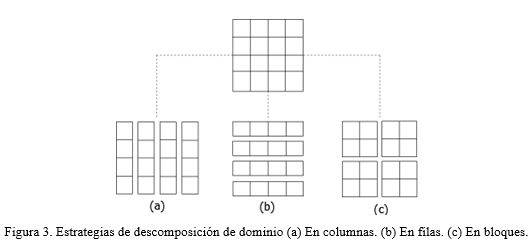
Los datos se dividen en subdominios más pequeños y cada una de las particiones obtenidas es asignada a un procesador, donde se ejecuta el algoritmo secuencial correspondiente (Wagner and Scott 1995) utilizando los datos del subdominio proporcionado. En los algoritmos paralelos para procesar información raster, comúnmente los datos se descomponen en subdominios rectangulares utilizando tres estrategias comunes: descomposición por filas, descomposición por columnas o descomposición en bloques (Qin et al. 2014a), Figura 3.

Los autores en (Wagner and Scott 1995) plantean que el rendimiento de un algoritmo paralelo con respecto a la descomposición de los datos, depende en gran medida de la correspondencia que exista entre el tamaño de los subdominios obtenidos y el balance en la asignación de estos subdominios a cada uno de los elementos de procesamiento. En este sentido, el equilibrio entre los procesadores se logra si se particionan los datos en subdominios del mismo tamaño, de manera que se logre uniformidad en la distribución y en consecuencia que algunos procesadores no operen con mayor cantidad de datos que otros.

Teniendo en cuenta los resultados obtenidos en las pruebas experimentales expuestas en (Guan and Clarke 2010; Qin, Zhan, Zhu and Zhou 2014a), en el presente trabajo se asume el esquema de descomposición de los datos en subdominios horizontales, dividiendo la matriz de entrada en bloques de filas.

En el algoritmo propuesto se inician tantos hilos como procesadores existan. Siendo p l número de procesadores y n la cantidad de filas de la matriz, entonces a cada procesador se le asigna un bloque de tamaño , Figura 4.

En el caso de que n no sea múltiplo de p, el último bloque tendría un tamaño de n - 2 mod p. De esta forma un procesador P_i cualquiera, recibe como parámetro a se denotan como sigue:

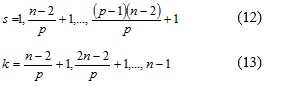
Esquema paralelo

En el esquema propuesto, la fuente de paralelismo radica en realizar la lectura de los datos de la matriz de entrada, realizar los cálculos correspondientes al algoritmo secuencial en paralelo y finalmente escribir los resultados en la matriz de salida, Figura 5.

El procesamiento se realiza en memoria compartida, empleando la técnica de programación OpenMP (Chapman et al. 2008). OpenMP es una API (del inglés Application Interface Programming) para los lenguajes de programación Fortran y C/C++ usada para implementar paralelismo en sistemas de memoria compartida. El modelo de programación paralela que aplica OpenMP es el Fork - Join, mediante el cual el hilo maestro genera hilos que se ejecutan en paralelo. OpenMP está compuesto por un conjunto de directivas que describen el paralelismo en el código fuente y denotan su portabilidad, pues en entornos que no usan OpenMP, las directivas son tratadas como simples comentarios e ignoradas. Además, proporciona capacidad para paralelizar de forma incremental un programa secuencial, independientemente del hardware.

Inicialmente, en el algoritmo paralelo propuesto (Algoritmo 2) se realiza la lectura del fichero raster de entrada (línea 1). En concordancia con los metadatos leídos se crea el fichero de salida (línea 2). Las matrices de entrada/salida se disponen en la memoria de la CPU en forma de buffer lineal, donde los elementos de la primera fila de la matriz se sitúan al inicio del buffer seguidos por los elementos de la segunda fila y así sucesivamente. Siendo m  la cantidad de columnas, el acceso a un espacio de índice ij  de A, en el buffer B  se realiza como sigue:

En la línea 4 del algoritmo se emplea una función para procesar las celdas correspondientes a los bordes del raster (filas 0 y n, columnas 0 y m) debido a la insuficiencia de datos para conformar la matriz de vecindad en estos casos. Luego, cada procesador P_i se desplaza por el bloque de filas que le corresponde procesar y para cada celda genera la matriz de vecindad correspondiente (líneas 5 - 23), almacenando el resultado del cálculo en el buffer de salida A' (línea 21). Seguidamente el hilo maestro se encarga de escribir estos resultados en el fichero de salida O (línea 23). Esta secuencia de pasos se encuentra formalizada en elAlgoritmo 2 que recibe como parámetros el fichero MDE para analizar (f) y el número de filas y columnas del mismo (n,m).

 

RESULTADOS Y DISCUSIÓN

El algoritmo fue implementado utilizando el lenguaje de programación C/C++. El tipo de planificación definida para determinar la cantidad de iteraciones asignadas a cada núcleo mediante OpenMP es estática (static), a través de la cual el algoritmo de planificación asigna bloques de iteraciones de igual tamaño a cada hilo.

Para evaluar el desempeño de los algoritmos propuestos se realizaron una serie de experimentos utilizando una PC Intel(R) Core(TM) i3-2120 con 4 núcleos de procesamiento a 3.30 GHz y 4 GB de memoria RAM.

Como fuente de datos para los experimentos se emplearon ficheros de tipo USGS ASCII DEM, VTP Binary Terrain, así como imágenes de tipo GeoTIFF. Los datos de las muestras de MDE empleadas en los experimentos se muestran en la Tabla 1.

La Tabla 2 muestra los tiempos de CPU obtenidos en la ejecución de la versión secuencial y la versión paralela propuesta para memoria compartida empleando las cuatro muestras de MDE descritas en la Tabla 1. Los resultados reflejan que, con la aplicación de la variante de procesamiento paralelo propuesta, los tiempos pueden ser mejorados de 30,253 a 14,205 segundos (en el caso del modelo M4), representando este valor una reducción aproximada del 53% del tiempo de ejecución en correspondencia con el algoritmo secuencial.

Adicionalmente, durante el proceso experimental se implementó una variante del Algoritmo 2. La diferencia radica en que en este caso el bucle interno es el que se ejecuta en paralelo tomando como variable privada de cada hilo a W. En las pruebas realizadas se evidenció un aumento del tiempo de ejecución con respecto a la primera versión. Este comportamiento se debe a que mediante OpenMP existe una barrera de sincronización de los hilos implícita al final de cada bucle y en este caso la sincronización se ejecutaría n  veces dentro del primer ciclo, lo que puede causar en ocasiones pérdida de rendimiento.

La gráfica de la Figura 6 muestra de manera comparativa los resultados reflejados en la tabla anterior.

En la gráfica de la Figura 7 se muestra el comportamiento de la ganancia de velocidad del algoritmo a medida que aumenta la cantidad de procesadores utilizados. Se puede observar que de manera general todas las muestras presentan similar comportamiento, indicando que el número óptimo de procesadores a utilizar debe ser cuatro, pues este es el caso en que se alcanza mayor ganancia de velocidad, manteniéndose relativamente cerca del óptimo teórico según la cantidad de procesadores.

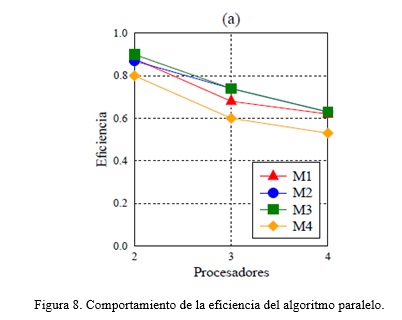
Sin embargo, se puede apreciar que aún cuando la ganancia de velocidad tiende a crecer relativamente cuando se utilizan cuatro procesadores, el óptimo teórico se acerca cuando se usan dos procesadores. Además, como muestra la gráfica de la Figura 8, la mayor eficiencia se alcanza de igual manera cuando se utilizan dos procesadores.

Un elemento importante a tener en cuenta cuando se trata de procesar MDE, es que el tiempo de procesamiento está dado por el tiempo de las operaciones de lectura y escritura (parte secuencial del algoritmo) sumado al tiempo de operaciones aritméticas para cada celda de la matriz (parte paralelizable). Por tanto, es de esperar que, en un momento dado, manteniendo el tamaño del MDE constante, aunque aumenten los procesadores a utilizar, se deje de ganar velocidad ya que se disminuye el tiempo de la parte paralelizable, pero el tiempo de la parte secuencial se mantiene constante, en este caso, la lectura y escritura de los ficheros.

 

CONCLUSIONES

En términos generales, los resultados obtenidos en los experimentos realizados se consideran satisfactorios, dada la mejora en términos de velocidad y rendimiento alcanzada.

Aunque en el presente trabajo se propone una variante paralela del algoritmo para el cálculo de la pendiente, la propuesta realizada puede ser aplicable a otros algoritmos de este tipo que describen funciones de análisis focal utilizando ventanas con tamaño n,

como es el caso del pre-procesamiento de los MDE para el análisis de modelos hidrológicos en la extracción de redes de drenaje, la extracción del índice de escabrosidad del terreno, así como su índice de posición topográfica.

Como trabajo futuro, se destaca la implementación de un mecanismo de procesamiento por bloques que permita procesar modelos que por su tamaño no pueden ser cargados completamente en la memoria RAM. El empleo de la memoria gráfica del sistema para la realización de cálculos en paralelo y la propuesta de esquemas híbridos usando mecanismos distribuidos.

 

REFERENCIAS BIBLIOGRÁFICAS

BARNES, R., C. LEHMAN AND D. MULLA. Distributed Parallel D8 Up-Slope Area Calculation in Digital Elevation Models. In International Conference on Parallel & Distributed Processing Techniques & Applications. 2011.

BERNHARD, J. An interactive approach to analytical relief shading. Cartographica,  2001, 38(1), 67-75.

BIESEMANS, J., M. V. MEIRVENNE AND D. GABRIELS Extending the rusle with the Monte Carlo error progagation technique to predict long-term average off-site sediment accumulation. Journal of Soil and Water Conservation,  2000, 55(1), 35-42.

CHAPMAN, B., G. JOST AND R. V. D. PAS. Using OpenMP. Portable Shared Memory Parallel Programming [online]. [Massachusetts Institute of Technology. London, England]: 2008.

FLEMING, M. D. AND R. M. HOFFER. Machine processing of Landsat mss data and lars. West Lafayette, Indiana: 1979.

FRAU, C. M., L. M. PINO, Y. O. ROJAS AND Y. M. HERNÁNDEZ Generalización de modelo digital de elevación condicionada por puntos críticos de terreno. Bol. Cienc. Geod,  2011, 17(3), 439–457.

GUAN, Q. AND K. CLARKE A general-purpose parallel raster processing programming library test application using a geographic cellular automata model. International Journal of Geographical Information Science,  2010, 24, 695-722.

HERLIHY, M. The Multicore Revolution. In S.B. HEIDELBERG ed. FSTTCS 2007: Foundations of Software Technology and Theoretical Computer Science. 2007.

HORN, B. K. P. Hill shading and the reflectance map. Proceedings of IEEE,  1981, 69(1), 14 - 47.

JIANG, L., G. TANG, X. LIU, X. SONG, et al. Parallel contributing area calculation with granularity control on massive grid terrain datasets. Computers & Geosciences,  2013, 60, 70-80.

MARTÍNEZ, Y. V. Modelo de Representación de Superficies de Terreno para su Visualización en Tres Dimensiones. Tesis doctoral Universidad de las Ciencias Informáticas, 2011.

NIKOLAKOPOULOS, K. G., E. K. KAMARATAKIS AND N. CHRYSOULAKIS SRTM vs ASTER elevation products. Comparison for two regions in Crete, Greece. International Journal of Remote Sensing,  2006, 27, 481–483.

QIN, C.-Z., L.-J. ZHAN, A.-X. ZHU AND C.-H. ZHOU A strategy for raster-based geocomputation under different parallel computing platforms. International Journal of Geographical Information Science,  2014a, 37-41.

QIN, C. Z., L. J. ZHAN AND A. X. ZHU How to apply the Geospatial Data Abstraction Library (GDAL) properly to parallel geospatial raster I/O? Transactions in GIS,  2014b.

RODRÍGUEZ, J. L. G. AND M. C. G. SUÁREZ Comparison of mathematical algorithms for determining the slope angle in GIS enviroment. Aqua-LAC,  2010, 2.

SEITAVUOPIO, P., J. RANTANEN AND J. YLIRUUSI Use of roughness maps in visualisation of surfaces. European Journal of Pharmaceutics and Biopharmaceutics,  2005, 59, 351-158s.

Análisis de la variabilidad del relieve a partir de modelos digitales del terreno. Rev. Sol. Geol,  1998, 11(1-2), 139-149.

WAGNER, D. F. AND M. S. SCOTT. Improving the performance of raster GIS: A comparison of approaches to parallelization of cost volume algorithms. In Computers, Autocarto Conference. 1995, p. 164–176.

ZEVENBERGEN, L. W. AND C. R. THORNE Quantitative analysis of land surface topography, earth surface processes and landforms. Proceedings of IEEE,  1987, 12(1), 47- 56.

ZHAN, L.-J. AND C.-Z. QIN Parallel Geospatial Raster Processing by Geospatial Data Abstraction Library (GDAL) — Applicability and Defects. Transactions in GIS,  2012.

ZHOU, Q. AND X. LIU Error analysis on grid-based slope and aspect algorithms. Photogrammetric Engineering & Remote Sensing,  2004, 70(8), 957–962.

 

 

Recibido: 25/03/2016
Aceptado: 30/06/2016