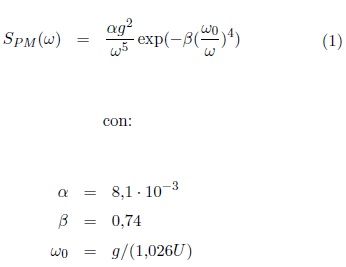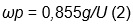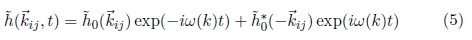Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
En la industria marítima, la simulación se ha convertido en una herramienta fundamental en la capacitación del personal especializado, la planificación estratégica y la predicción eficiente, reduciendo sustancialmente la necesidad de prototipos físicos. La simulación permite reproducir el comportamiento de un sistema en determinadas condiciones. Ofrecer un ambiente virtual, seguro y totalmente controlado, constituye su propósito fundamental (Krijt, 2014).
Un factor indispensable para la elaboración y la implementación de un simulador marino en general, lo constituye el modelado y la simulación de la superficie del mar; debido a que las olas constituyen uno de los elementos que perturban la estabilidad de un vehículo en el mar. La simulación de la superficie del océano, a su vez representa un gran desafío, ya que las olas constituyen un fenómeno natural complejo, que cambian continuamente a causa de la velocidad del viento y otros factores (Lining et˜al., 2017; Lastra et˜al., 2018; Jeschke, 2017).
El proceso de simulación puede asumir distintas aristas destinadas a varios tipos de aplicaciones: la simulación física y la representación visual. La primera define la deformación de la superficie en el dominio del tiempo, mientras que la segunda compone el aspecto visual de esta. En ambos casos, existen factores con diferentes niveles de complejidad que influencian el resultado final. Entre ellos, la representación y el tiempo real, constituyen dos objetivos esenciales para evaluar los resultados (He etal., 2005).
Para lograr este proceso deben considerarse una serie de aspectos que a continuación se detallan:
Representación de la superficie: Las técnicas para la representación de la superficie del mar proponen esquemas de visualización, a partir de discretizaciones gráficas compuestas por arreglos de celdas básicas (Tessendorf, 2004). Para los simuladores de entrenamiento la técnica seleccionada debe ser lo suficientemente precisa y simple, de manera que sea posible cumplir con los requerimientos computacionales de una aplicación en tiempo real (Madushani et˜al., 2016). El cálculo mediante el cual se obtiene el valor correspondiente a la altura de la ola en cada punto de la superficie es realizado mediante un modelo matemático que debe definir con precisión las características del entorno de simulación (Krijt, 2014).
Representación de otros elementos visuales: La incorporación a la visualización de fenómenos como la interacción entre la luz y el agua permiten una simulación más realista del fluido (Mitchell, 2005). Atendiendo a las propiedades o´pticas de la superficie del océano, se necesita implementar un conjunto de funciones ma- temáticas que permitan la representación de estos efectos. Dentro de estos efectos, los más importantes son las inversiones térmicas y de humedad, variaciones del índice de refracción (espejismos inferior y superior) y las dispersiones.
Motor gráfico: Es la interfaz principal para la implementación del mundo virtual. La funcionalidad básica de un motor gráfico es proveer al sistema con herramientas de renderizado para los gráficos 2D y 3D, admi- nistración de memoria, entre otras. Existen gran cantidad de motores gráficos para tiempo real, pero pocos reu´nen las condiciones de gratuidad, licencia de código abierto y desarrollo en C++ (Varela, 2015).
El presente trabajo se organiza como sigue. En la primera Sección se presenta el modelo utilizado por la aplicación DEPTHWAVE para la simulación gráfica del comportamiento del mar, lo cual constituye la principal contribución de este trabajo. El ambiente de desarrollo y las herramientas empleadas entre las cuales se destaca el motor gráfico OGRE3D y el complemento Hydrax son abordas en la segunda Sección. En la tercera Sección se muestra un análisis de los resultados alcanzados, el comportamiento y la configuración de la aplicación enfatizando en los requerimientos de realismo requeridos. Las conclusiones y trabajo futuro son presentados en la cuarta Sección.
MATERIALES Y MÉTODOS
La reproducción del oleaje constituye un problema de investigación abierto y uno de los grandes desafíos de la computación gráfica (Lining etal., 2017; Jin, 2018). En particular la simulación realista de la superficie oceánica, retomada e impulsada por Tessendorf (Tessendorf, 2001), continuá siendo de gran interés en varios campos, tales como: la industria cinematográfica, la realización de videojuegos y el desarrollo de herramientas de simulación oceanografía en ambientes interactivos (Fréchot, 2006).
Representación matemática del oleaje
Las representaciones basadas en espectros de energía constituyen una alternativa viable para lograr modelos de oleaje con las propiedades de realismo y aleatoriedad que requiere la simulación de este fenómeno (Ochi, 1998). Debido a que la fluctuación aleatoria de la superficie del mar se atribuye generalmente a la energía transferida por el viento al océano, la energía potencial y cinemática de olas aleatorias es representada por la función de densidad del espectro, que a su vez tiene un valor significativo en la evaluación de las propiedades estadísticas de las olas aleatorias.Esta función de densidad espectral o espectro de onda S(ω, θ) , expresa la energía promedio en el tiempo de una configuración de océano aleatorio, como una función continua de frecuencia angular ω y dirección θ.
Aunque a partir de esta teoría han sido desarrolladas varias funciones de espectros, en el presente trabajo se propone emplear el espectro de Pierson Moskowitz, (Pierson, 1964) propuesto a partir del estudio realizado por meteorólogos británicos en el Atlántico Norte para determinar empíricamente los coeficientes de una función de espectro basada en el rango de equilibrio de Phillips (Ochi, 1998). Este espectro de energía permite generar mares totalmente desarrollados a partir de una velocidad del viento definida y su dirección obteniéndose para diferentes configuraciones los estados del mar deseados (Ochi, 1998). Numerosos son los trabajos que utilizan este tipo de espectro en aplicaciones relacionadas con la simulación de la superficie del mar (Anil, 2016; Chen, 2013; Madushani et˜al., 2016).
La ecuación 1 representa la distribución de la energía de las olas entre las diferentes frecuencias de onda en la superficie del mar.
En donde g es la gravedad y U es la velocidad del viento a una altura de 10m sobre el nivel del mar. La frecuencia pico ωp, es la frecuencia angular para la cual las olas tienen en su mayoría energía promedio. La ecuación 2 representa su forma de cálculo para este espectro.
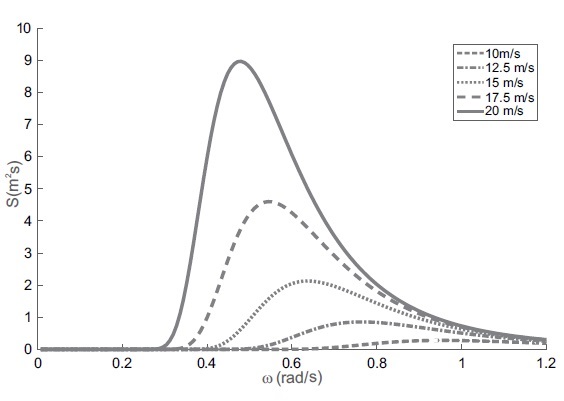
La Figura 1 contiene la visualización del espectro para diferentes velocidades del viento. Los modelos estadísticos inspirados en esta teoría a partir de observaciones experimentales, consideran la altura de la ola h(x, t) como una variable aleatoria de la posición horizontal y el tiempo. Estos modelos se basan en la capacidad de descomponer el campo de altura de las olas como una suma de ondas sinusoidales y cosenos.
Para lograr esta representación se requiere discretizar el espacio en una malla regular de N × M puntos con dimensiones Lx ×Ly sobre la cual es estimada la altura. El uso de la Transformada Rápida de Fourier (FFT ) es introducido en el modelado, ya que constituye una poderosa alternativa para calcular rápidamente el campo de altura, al ser una forma eficiente de computar la suma de números complejos (Mastin etal., 1987; Premoˇze, 2000; Tessendorf, 2001; Fréchot, 2007; Lining et˜al., 2014). La ecuación 3 expresa la transformación del conjunto N × M de números complejos Fn,m en el conjunto de nu´meros complejos fp,q, donde p ∈ {1,. . . , N } y q ∈ {1,. . . , M }.
El modelo de representado en la ecuación 4 muestra la solución de las alturas de la superficie en términos de FFT para calcular el campo de altura.
La variable del miembro izquierdo de la ecuación 4 representa la elevación de la superficie del mar,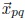 
denota la posición horizontal 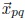= (xp, yq) = (Lp/n, Lq/n), t es el tiempo y 
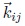es el vector del número de onda, el cual cumple con la siguiente condición 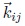= (kx,i, ky,i) = (2πi/L, 2πj/L) para un ancho L de la superficie representada. Además p, q, i, j son números enteros, tal que −n/2 ≤ p, q, i, j < n/2 y n, m son enteros positivos relacionados de la siguiente manera n = 2
m
.
Las amplitudes de Fourier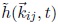 
del campo de altura de la ola pueden generarse en un tiempo t, a partir de la relación de dispersión ω(κ) de la siguiente manera:
La relación de dispersión ω(κ) expresa la relación funcional entre la velocidad de propagación y la longitud de la onda, dependiente de la gravedad, la profundidad del océano y otros parámetros físicos (Horvath, 2015). Las amplitudes de Fourier dependientes del tiempo 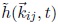se obtienen al combinar los resultados obtenidos para las amplitudes del campo de altura 
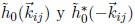reproducidas para el ángulo de fase 
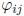según la ecuación 6 y su número complejo conjugado, respectivamente. El término de fase 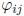para proveer un modelo aleatorio de olas, se obtiene según una distribución aleatoria uniforme entre [0 : 2π] (Ochi, 1998).
Ambiente de desarrollo
La generación y deformación de la superficie del mar que implementa la aplicación DEPTHWAVE mediante el modelo anterior se descompone en cuatro pasos fundamentales:
Generación del estado de mar con el modelo de espectro de ondas de Pierson Moskowitz.
Identificación de los componentes (sistemas de onda) representados por la superficie del mar.
Cálculo de la energía de los sistemas de ondas.
Deformación de la superficie (dada por un campo de elevaciones).
La generación del estado de mar sobre la base del modelo de espectro descrito consiste esencialmente en definir la función espectral en el ámbito de la frecuencia a partir de parámetros físicos o estadísticos de los que depende. Basadas en el espectro de Pierson-Moskowitz se desarrollaron relaciones entre la velocidad del viento y la frecuencia pico del espectro, y posteriormente entre esta última y la altura significativa de onda, como se describe en (Ochi, 1998). Así, el modelo virtual prevé también la generación de un determinado estado de mar a partir de los parámetros estadísticos mencionados. La discretización del espectro determina el conjunto finito de sistemas de ondas representado visualmente por la superficie del mar. Cada componente (sistema de ondas) contiene la energía existente en una gama específica de frecuencias y direcciones de propagación definidas por el espectro. La simulación numérica tridimensional de la superficie del mar sólo es viable recurriendo a las FFT.
Típicamente, la distribución de la energía de los modelos de espectros direccionales se da en función de la frecuencia y de la dirección de propagación de las ondas. Sin embargo, sólo es posible discretizar el espectro uniformemente en ambas direcciones si se define en el espacio de vectores de onda. El cálculo para la deformación de la superficie del mar implica determinar la energía del sistema de ondas definido para la malla de simulación. Para representar las escenas que se simulan en el presente trabajo se utiliza el motor gráfico OGRE3D. Se selecciona este motor gráfico debido a que es un motor de software libre, multiplataforma y de código abierto. Este motor gráfico está hecho principalmente para realizar aplicaciones tridimensionales. OGRE3D brinda soporte para las Interfaces de Programación de Aplicaciones (API, por sus siglas en inglés) OpenGL y Direct3D, además facilita el trabajo de los desarrolladores en comparación con dichas API. También cuenta con una comunidad activa y presenta una interfaz entendible y fácil de usar (Junker, 2006).
Como lenguaje de programación para implementar la aplicación se selecciona el lenguaje C++. Las principales características de este lenguaje por las cuales fue seleccionado son: lenguaje potente, orientado a objetos, multiplataforma y libre. Este lenguaje permite la reutilización de código mediante la herencia, la sobrecarga de operadores y de funciones. Además, es uno de los lenguajes más utilizados en el mundo para la creación de aplicaciones relacionadas con la realidad virtual.
Como metodología de desarrollo de software se selecciona Rational Unified Process (RUP). La selección de esta metodología facilita el desarrollo de un producto mediante iteraciones con hitos bien definidos, donde se repiten las actividades, pero con diferentes énfasis. Esta metodología permite el desarrollo de software a gran escala, mediante un proceso continuo de desarrollo. Mediante esta se modelan visualmente los productos de software empleando el Lenguaje de Modelado Unificado (UML, por sus siglas en inglés). Esta es una metodología dirigida por casos de uso, donde los casos de uso guían el proceso de desarrollo.
Otra importante característica está relacionada con la arquitectura, la cual puede ser descrita en diferentes vistas. Además, es una metodología iterativa e incremental, por lo que divide el desarrollo en pequeñas partes que al concluir aportan un incremento al producto final.El uso del IDE Qt Creator conjuntamente con el motor gráfico OGRE3D y con el lenguaje C++ hizo posible el funcionamiento de las herramientas y la ejecución la aplicación.
RESULTADOS Y DISCUSIÓN
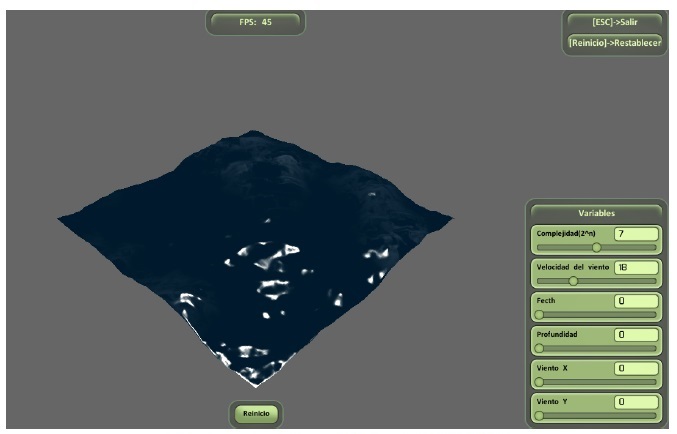
Teniendo en cuenta el propósito específico de la simulación, la representación de la superficie del mar constituye uno de los principales elementos de distinción. Tomando lo antes expuesto como punto de partida, a continuación se realiza la validación del modelo implementado y se ilustra cómo los diferentes elementos visuales incorporados a la simulación permiten recrear una escena más realista de la superficie, así como del ambiente de interacción. La Figura 2 muestra la interfaz de la aplicación DEPTHWAVE utilizada en las simulaciones.
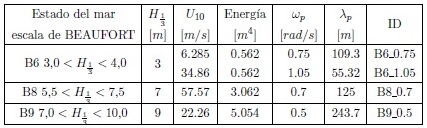
Los resultados muestran el realismo visual esperado para cada estado de mar en correspondencia a la Tabla 1.
Se puede observar en la Figura 3(a) y Figura 3(b), ambas representan estados de mar con alturas significativas de 3,0m, de manera que las ondas son bastante menores que las representadas en la Figura 3(c) y Figura 3(d), con alturas significativas de 7,0 y 9,0m respectivamente. La superficie del mar en la Figura 3(a) es bastante más regular, y el swell mucho más perceptible. Lo mismo ocurre en las imágenes debajo donde la Figura 3(d) muestra un swell más pronunciado.
CONCLUSIONES
En el presente trabajo se presenta la aplicación DEPTHWAVE para la simulación gráfica del comportamiento del estado del mar desarrollada bajo la distribución de softwatre libre del motor gráfico OGRE3D. El modelo matemático representa al espectro de Pierson Moskowitz permitiendo el uso de datos estadísticos, derivados de la oceanografía física y por tanto realizar la simulación atendiendo a estos criterios, contando con la suficiente exactitud para poder representar mediante simulación los distintos estados del mar y la visualización de diferentes efectos visuales. Como parte de la continuidad de este trabajo, se pretende extender la experimentación incorporando otros espectros de oleaje, con el propósito de evaluar su efectividad atendiendo al realismo y los requerimientos de tiempo real necesarios en este tipo de aplicación.
